同轴离心式喷嘴热声不稳定性递归分析

杨向明，杨尚荣，杨岸龙，艾春安

(1. 火箭军工程大学， 西安 710025； 2. 西安航天动力研究所液体火箭发动机技术重点实验室， 西安 710100)

0 引 言

热声不稳定是火焰、流场和声场间非线性耦合的结果，其本质是非线性系统[1]。因此，可以采用非线性时间序列方法，从动力系统角度分析非线性热声系统的动力学特征，寻求不同动力学状态间转变的控制参数，进而对热声不稳定进行提前预报和控制[2]。

非线性时间序列分析方法中，非线性不变量，如分形维数、最大Lyapunov指数分别表征系统在相空间中的静态和动态结构，熵代表信息生成率，均被用来分析热声系统的动力学特性。Kabiraj等[3]利用关联维数和最大Lyapunov指数研究了管道层流预混燃烧系统的热声振荡现象。Gotoda等研究了贫燃预混旋流稳定湍流火焰的动力学特性，发现平移误差[4]、排列熵[5]均可作为监测贫燃熄灭极限的指标。

另一类基于动力系统递归性质的非线性时间序列方法，如递归图和递归量化分析方法，可以从热声系统中的标量时间序列中获得更多系统动力学方面的特性，在热声系统动力学分析中得到了较多应用。文献[6-7]采用递归图分析方法，在钝体稳焰湍流燃烧器中，发现在热声不稳定发生之前，高幅值的周期振荡总会阵发性出现，直到热声不稳定发生为止，这种阵发性现象也被多项实验证实[8-9]。Sen等[10]利用递归量化方法对管道逆扩散火焰进行了研究，发现了极限环、阵发和同宿异轨等现象。Gotoda等[11]利用递归图、多尺度熵等方法研究了贫燃预混旋流稳定湍流火焰的动力学特性，发现在接近贫燃熄灭边界时，存在混沌向周期振荡转变的随机过程，继续增加当量比，周期振荡通过准周期振荡又转变为混沌[12]。Unni等[13]分别利用广义的赫斯特指数和递归量化分析方法，在同一框架内对湍流燃烧系统中的热声不稳定和贫燃熄灭[14]两种现象进行了预报。结合递归图、递归网络方法和同步理论[15-16]，学者发现非稳态热释放率对声压的影响更大(相比声压对非稳态热释放率的影响)，因此认为消除热声不稳定时控制火焰比控制声场更有效。

液体火箭发动机中的热声不稳定是发动机研制过程中必须解决的关键难题。同轴离心式喷嘴作为最常用的液体火箭发动机双组元喷嘴，对其燃烧稳定性的研究一直受到学者们关注。王枫等[17]利用相似准则设计了缩比燃烧室，发现喷嘴缩进长度对燃烧稳定性裕量有很大影响。王迪等[18]开展了气液同轴离心式单喷嘴模型发动机试验，发现喷嘴缩进长度的增加对纵向高频燃烧不稳定性产生阻尼作用。燃烧室长度对纵向高频燃烧不稳定性的影响比喷嘴缩进长度更明显。王延涛等[19]试验发现同轴离心喷嘴的自发激励高频燃烧不稳定过程出现了“滞后”现象，不稳定性工况下的火焰均为脱口火焰，火焰特征长度约等于喷嘴出口到脱口火焰团上沿的距离。

本文开展同轴离心式喷嘴稳定性试验研究，采用递归图和递归量化分析方法对实验结果进行讨论，从动力系统角度分析同轴离心式喷嘴火焰动力学特性，为液体火箭发动机热声不稳定性预报和控制提供理论支持。

1 实验系统和数据处理方法

1.1 实验装置

燃烧试验系统原理如图1所示。模拟燃烧室为敞口圆筒形结构，直径Dc= 156 mm，高Hc=277 mm，垂直安放在模拟喷注器面板(水冷平板)上。试验用喷嘴(见图2)为带缩进室的同轴离心喷嘴，由外喷嘴和内喷嘴组成，外喷嘴为离心煤油喷嘴，出口直径Df= 16.4 mm，内喷嘴为直流氧化剂喷嘴，出口直径Do=13.4 mm。缩进室长度为10.5 mm。喷嘴安装于模拟燃烧室中间位置，出口与模拟喷注器面板平齐。

试验用氧化剂为400 ℃的氧气与空气混合形成的富氧气，试验用燃料为410 ℃的煤油蒸气，采用气气湍流扩散燃烧可以有效模拟液氧煤油补燃循环液体火箭发动机推力室的燃烧稳定性状态[17]。氧气和空气的混合物用氧化剂换热器加热，煤油用燃料换热器加热为煤油蒸气。

1.2 试验方法和工况

脉动压力传感器数目为1只，安装在模拟燃烧室壁面距模拟喷注器面板20 mm的位置(见图1)，型号为Kistler 6043A型，与高速数字采集系统LMS相连，采样记录频率为12.8 kHz。试验中，稳定燃料流量，逐步增加氧化剂流量至各工况点，如表1所示。混合比为氧化剂(84% 氧气+16%空气)与燃料(煤油)质量流量之比。

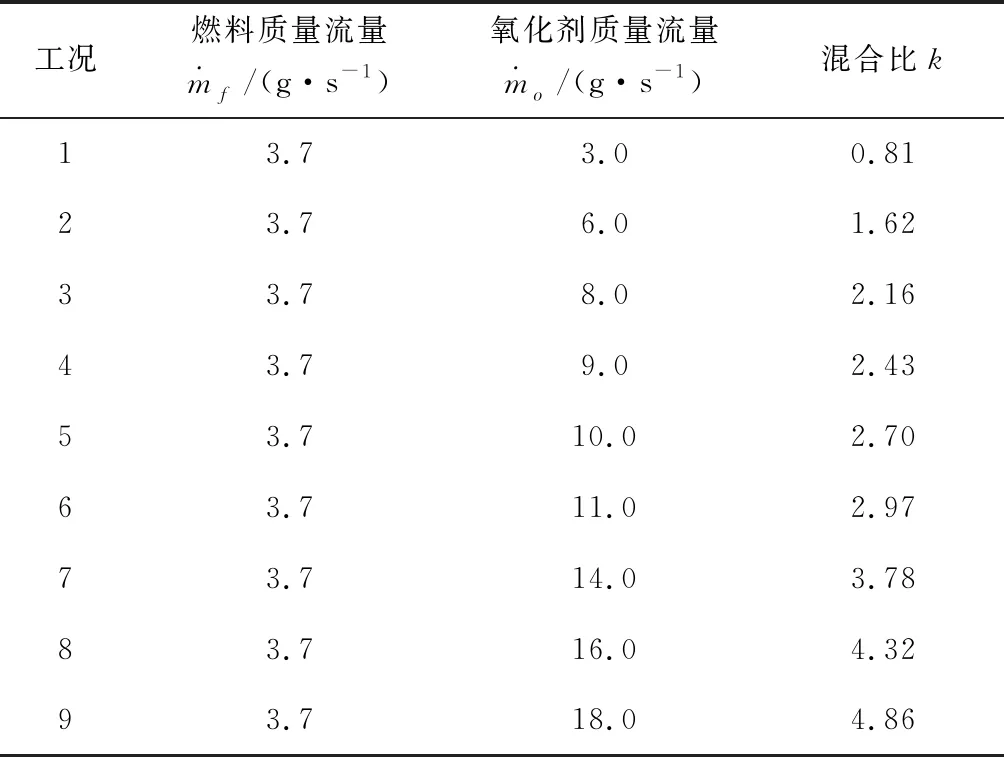
表1 试验工况Table 1 Test operating conditions

1.3 数据处理方法

1.3.1相空间重构

相空间重构是非线性时间序列分析的基础。对于压力时间序列{x(i)|i=1,…,n}，由时间延迟重构技术可以得到延迟向量[20]

yi=y(i)=(x(i),x(i+τ),…,x(i+(d-1)τ)),

i=1,2,…,n-(d-1)τ

(1)

式中：d为嵌入维数，通过虚假最邻近法(False nearest neighbor，FNN)确定；τ为延迟时间，取采样间隔的整数倍，通过互信息法(Average mutual information，AMI)确定。

1.3.2递归分析

对于确定性系统，递归是其固有本质特性[10]。递归图用来显示和分析系统在相空间中的动力学行为。二进制矩阵R称为递归矩阵，如果yi是yj的邻近点，则矩阵元素Rij等于1，否则矩阵元素Rij等于0。数学上写为

(2)

式中：Θ为Heaviside函数；ε为两点间的最大距离，称为递归阈值；M=n-(d-1)τ为重构相空间中向量的数量；两条轨迹间的距离通过L2范数进行计算。递归图中，白点表示0，黑点表示1。因为Rii=1，因此任何递归图的主对角线上全部为黑点。

递归图中线性结构的量化分析通常利用下述几种测度。

1) 递归率：

(3)

递归率表示了黑点在递归图中的密度，代表相空间中递归的比例分数。

2) 确定率：

(4)

确定率是递归图对角结构递归点比例分数的测度，是系统周期行为的测度。P(l)是长度为l的对角线数量，lmin是构成对角结构的最小点数目。本文中，lmin假定为5。

3) 对角线平均长度:

(5)

平均对角线长度量化评估两段轨迹保持在彼此邻域的平均时间，对角线平均长度减小意味着混沌行为增加。

4) 层状度：

(6)

层状度表征组成竖直结构的递归点的比例分数。递归图中，竖直结构表示层流状态或阵发性。与确定率相似，P(v)是长度为v的竖直线数量，vmin是构成竖直结构的最小点数目。本文中，vmin假定为3。

5) 捕获时间：

(7)

系统在某一特定状态花费的平均时间可用捕获时间定量描述，也是递归图中竖直结构的平均长度。

上述测度在本文中用来定量表征热声系统的动力学特性。

2 实验结果及分析

2.1 频率和幅值

试验中燃料流量不变，随着氧化剂流量的增加(混合比增加)，系统从稳定状态变为热声不稳定状态。图3中列出了典型工况下(混合比0.81,2.97,4.32)的压力时间序列和FFT分析结果。从图3可以看出，混合比0.81时系统出现了低幅值的宽频振荡，主要为推进剂流动激发的燃烧器低阶声腔模态，没有发生热声耦合，为稳定状态。混合比为2.97和4.32时，系统为不稳定状态，出现了多个频率的振荡。

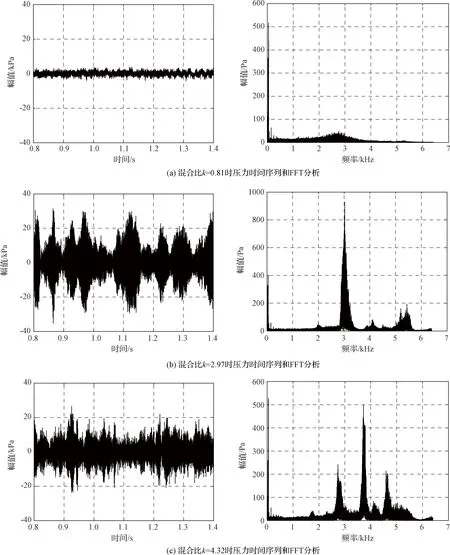
图3 不同混合比条件下的压力时间序列和FFT分析Fig.3 Pressure time series and FFT analysis for different mixture ratios

理论计算燃烧室固有声模态频率时，假定各处声速相同，纵向声频率按下式计算(一端开边界、一端闭边界)[21]

(8)

其中，c为声速，L为燃烧室纵向长度，n为声模态阶数。切向声频率利用贝塞尔函数计算，其前两阶α值分别为1.8411和3.0542。计算得到模型燃烧室前五阶频率如表2所示(声速约为1010 m/s)。试验中出现的频率为2736 Hz,3722 Hz,4660 Hz(混合比4.32)。由此可知，试验中出现的不稳定频率为燃烧室第二、第三阶纵向和第一阶切向声模态频率。根据定义[20]，它们为无公度振荡频率(系数为有理数时振荡频率线性不相关)。

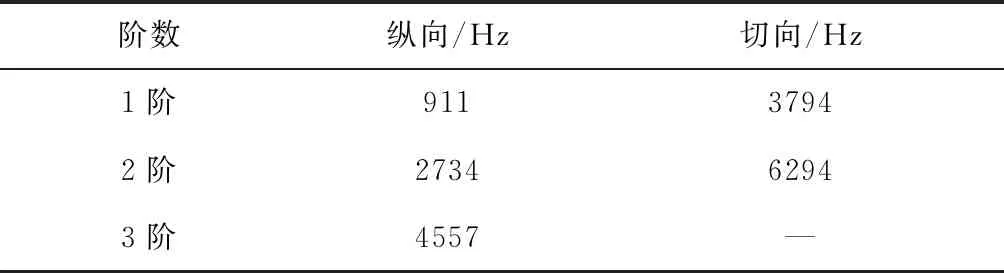
表2 燃烧室前五阶频率Table 2 The first five modes of chamber

不同混合比下的最大振荡幅值如图4所示。在混合比为2.70时，模拟燃烧室出现了自激燃烧不稳定，混合比为2.97时，振荡幅值达到最大，继续增加混合比，振荡幅值有所下降。需要注意的是，不同混合比下最大幅值对应的振荡频率并不相同，混合比为2.97时，第二阶纵向声模态频率为3022 Hz。混合比变化时，火焰结构和动力学发生变化，引起局部声阻抗和声速的变化，因此系统振荡频率也会发生变化[14]。

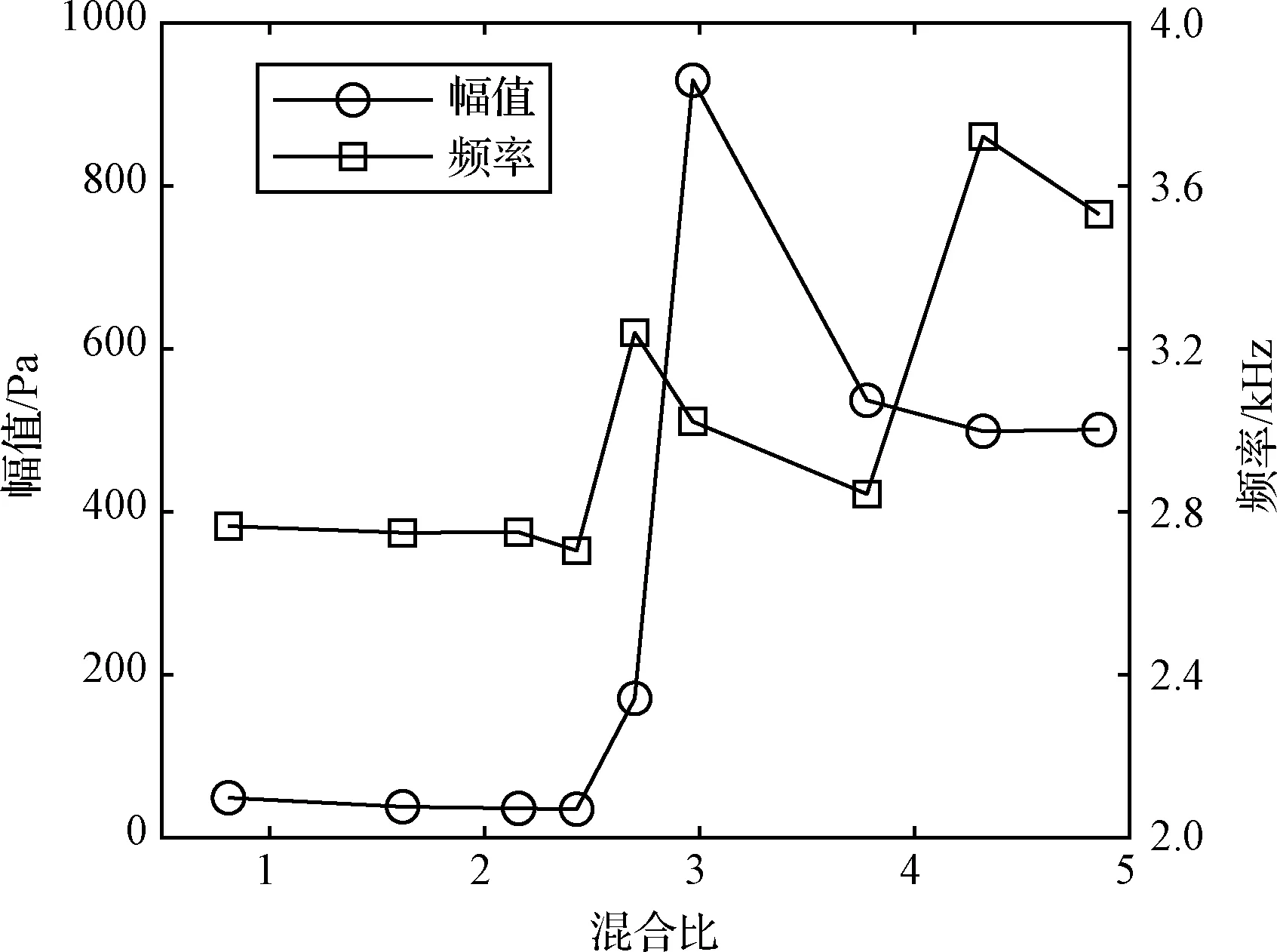
图4 不同混合比下最大幅值和对应的频率Fig.4 Maximum amplitudes of FFT spectrum and corresponding frequencies at different mixture ratios

2.2 相空间重构

采用交互信息法求最优延迟时间τ时，取互信息法的第一个局部最小值为最优延迟时间[21]。求得混合比为0.81，2.97，4.32时最优延迟时间τ分别为0.11 ms,0.07 ms,0.07 ms，嵌入维数d分别为15，9，8。

利用最优延迟时间τ和最小嵌入维数d，绘制了混合比为0.81，2.97，4.32时的相空间轨迹图(见图5)。从图5可以看出，混合比0.81时相轨迹图为无序轨迹线的聚集，振荡幅值比较低，为典型的燃烧噪声轨迹图。混合比2.97时相轨迹图在高幅值周期振荡(外部圆)和低幅值振荡(内部小区域)之间连续转变，具有阵发现象的特征[8]。混合比4.32时相轨迹图虽然看似也为无序轨迹，但其振荡幅值较高。由第2.1节可知，混合比4.32时其无公度振荡频率多于2(无公度振荡频率为2时相轨迹为环面[20])，因此相轨迹图也显示出类似无序状态。

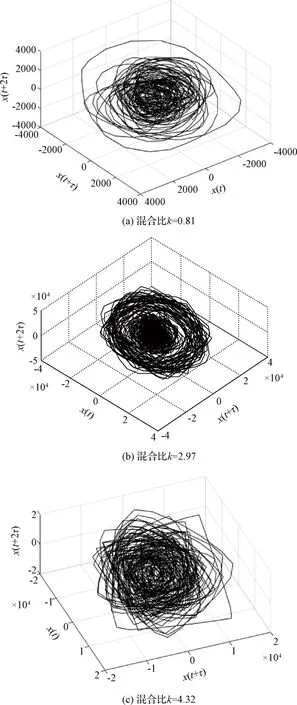
图5 三种混合比下的相空间轨迹图Fig.5 Phase space trajectory for three different mixture ratios

3 递归分析

3.1 递归图

计算不同混合比下压力时间序列的递归图，发现混合比为0.81～2.43时的递归图相近，混合比为2.7和2.97时的递归图相近，混合比为3.78～4.86时的递归图相近，因此下文以混合比为0.81，2.97，4.32时的递归图作为典型结果进行分析。递归阈值ε依据吸引子直径按比例选取，如ε=0.1，说明递归阈值ε取值为吸引子直径的10%。

混合比0.81时声压振荡幅值较低，为燃烧噪声状态，从递归图6可以看出，整体呈现一种较为均匀的分布特征。进一步分析，发现存在与主对角线平行的短线，证明系统可能存在周期性过程(确定性)，而白色噪声过程(随机的)状态为均匀分布的黑点[20]。

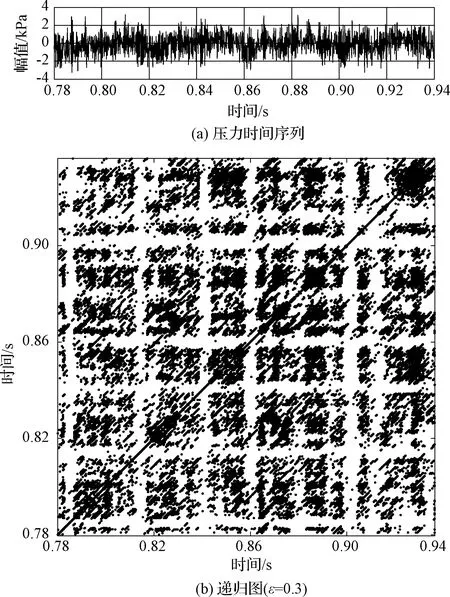
图6 混合比k=0.81时压力时间序列和递归图Fig.6 Pressure time series and recurrence plot for mixture ratio k=0.81

混合比2.97时压力时间曲线和对应的递归图如图7所示，压力时间曲线上显示高低幅值交替出现，递归图上出现了密度较大和白色区域交替出现的现象。与压力时间曲线对应可以发现，密度较大的黑色方块对应于幅值较低的阶段，白色区域对应于高幅值阶段。这种白色区域和黑色方块区域交替出现是阵发现象的典型特征。依据阵发现象的定义[23]，递归图(见图7(b))上出现的密度较大的黑色方块对应于层流状态(阵发之前的动力学状态)，层流状态被阵发状态隔开。黑色方块右上角上都有曲线延伸出去，形成“风筝”状图形，这是第II类阵发的特征[23]。出现第Ⅱ类阵发意味着系统发生了亚临界Hopf分叉，即系统由一个稳定平衡点和一个不稳定周期解转变为单个不稳定平衡点。发生亚临界Hopf分叉时，系统行为与初始条件有关，存在双稳定区或滞后区现象，在前期的试验中得到了验证[19]。

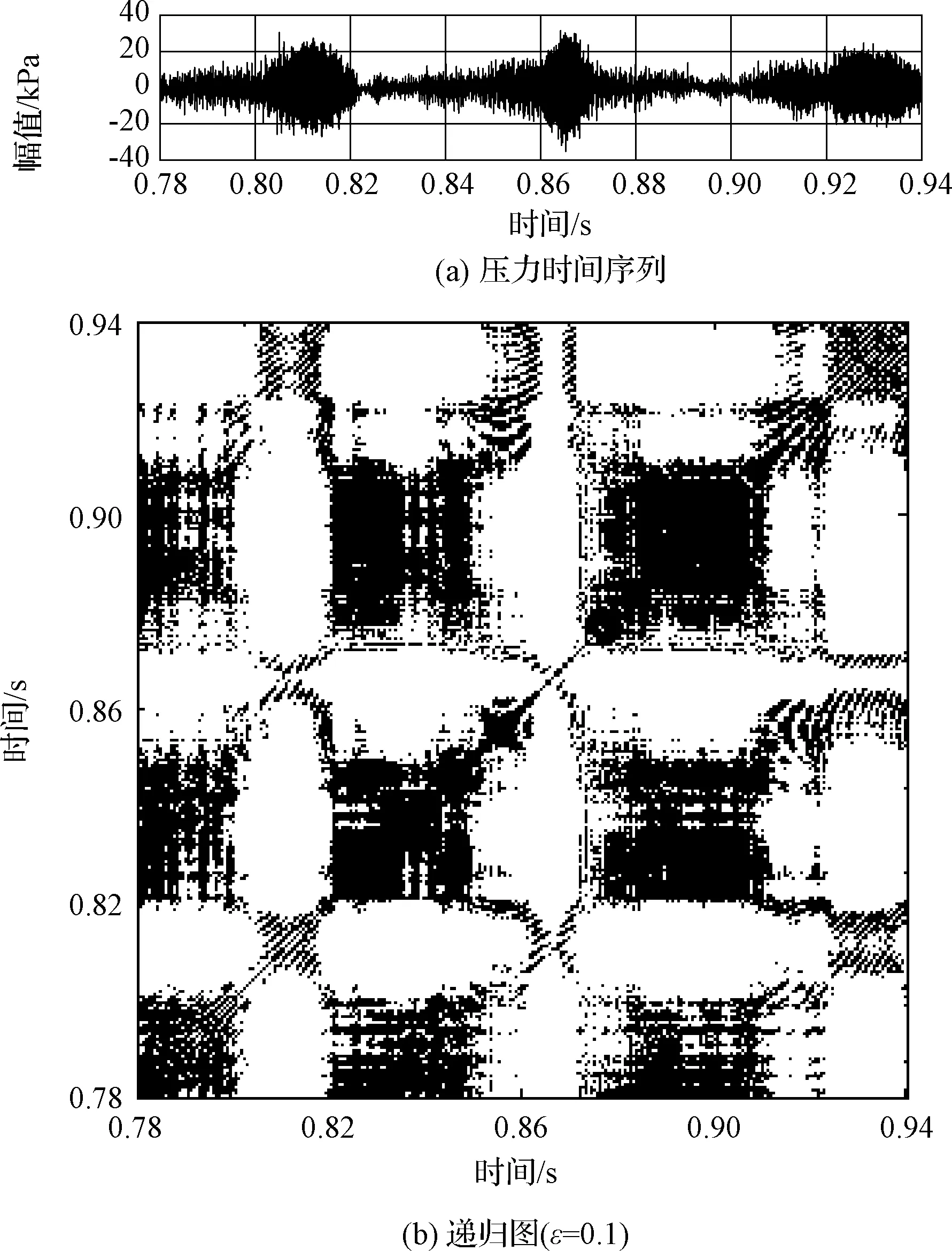
图7 混合比k=2.97时压力时间序列和递归图Fig.7 Pressure time series and recurrence plot for mixture ratio k=2.97

图8为从图7(b)中沿对角线截取的窗口，代表着系统时间发展历程。进入阵发之前，系统为准周期振荡状态b，逐渐地，系统从准周期状态进入了周期振荡状态c和d。

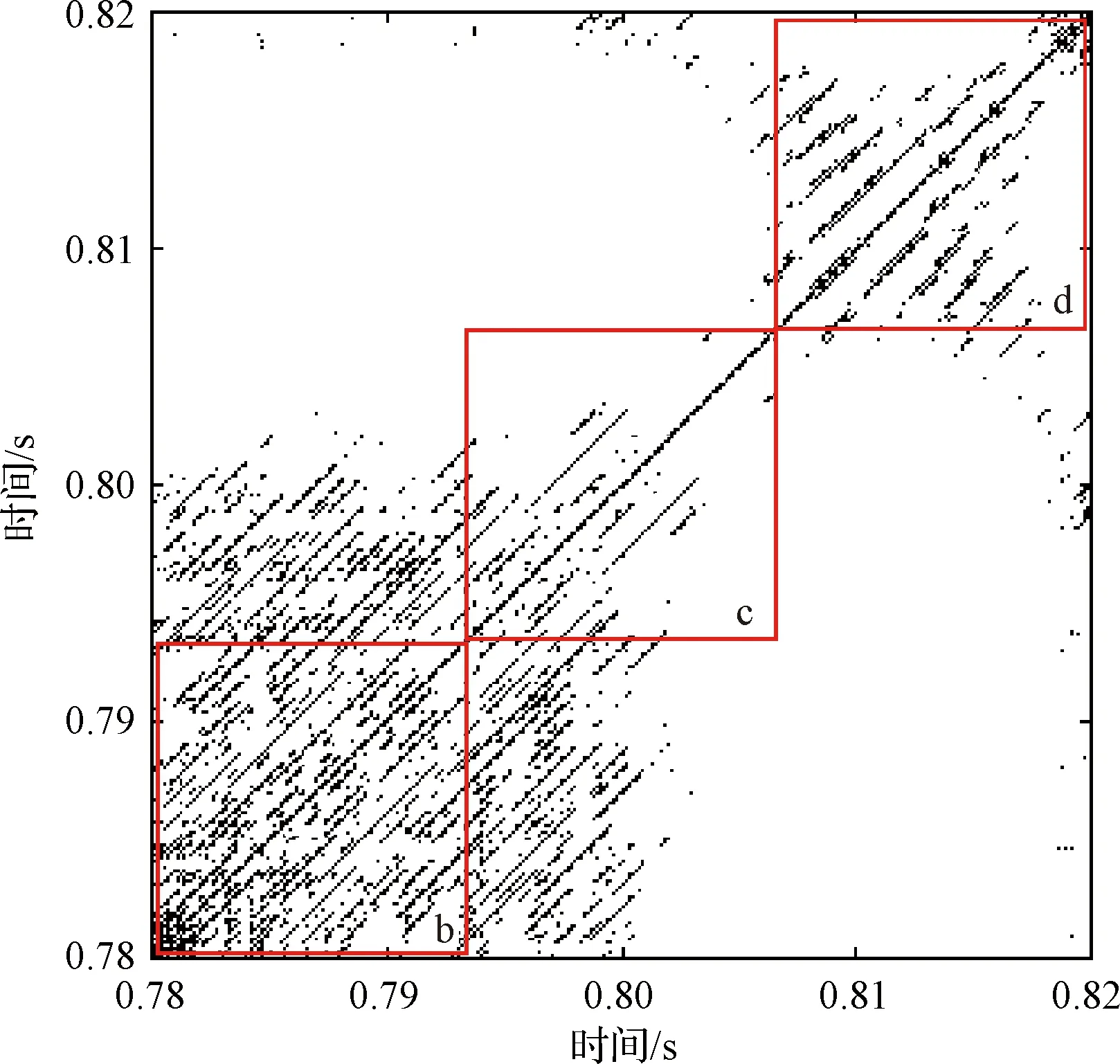
图8 混合比k=2.97时动力学状态转变过程Fig.8 Transition process of dynamic state for mixture ratio k=2.97

混合比4.32时时间曲线和递归图如图9所示。时间曲线上压力振荡幅值相对稳定，没有出现混合比2.97中高低幅值振荡交替的现象。从递归图9可以看出，存在与对角线平行的分段的短线，说明系统存在周期性过程。结合第2.1节频谱分析，此工况下系统出现了3种无公度频率的振荡，根据定义，系统为准周期振荡状态。递归图符合准周期振荡的特征：准周期振荡会打断较长的对角线，因此递归图中会显示出与对角线平行的分段的短线[21]。

3.2 递归量化分析

采用递归量化分析方法，计算各实验工况下递归率、确定率、对角线平均长度、层状度和捕获时间等参数值。计算共采用时长0.78 s的数据点(10000个数据点)，分成20段(每段500个数据点)单独进行递归分析，然后计算出平均值和标准差。递归阈值ε取为吸引子直径的0.1[21]，计算结果如图10所示。

递归率中，混合比为2.97时数值最大，对应于阵发现象，其它工况下数值相当。

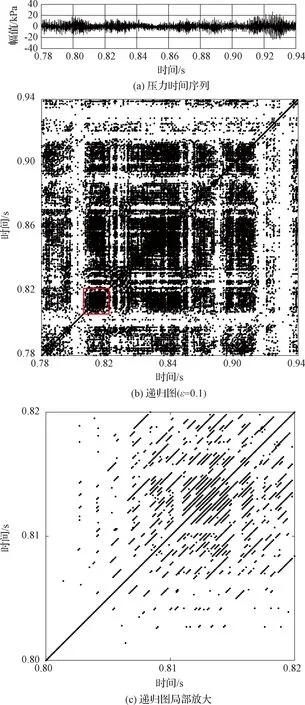
图9 混合比k=4.32时压力时间序列和递归图Fig.9 Pressure time series and recurrence plot for mixture ratio k=4.32

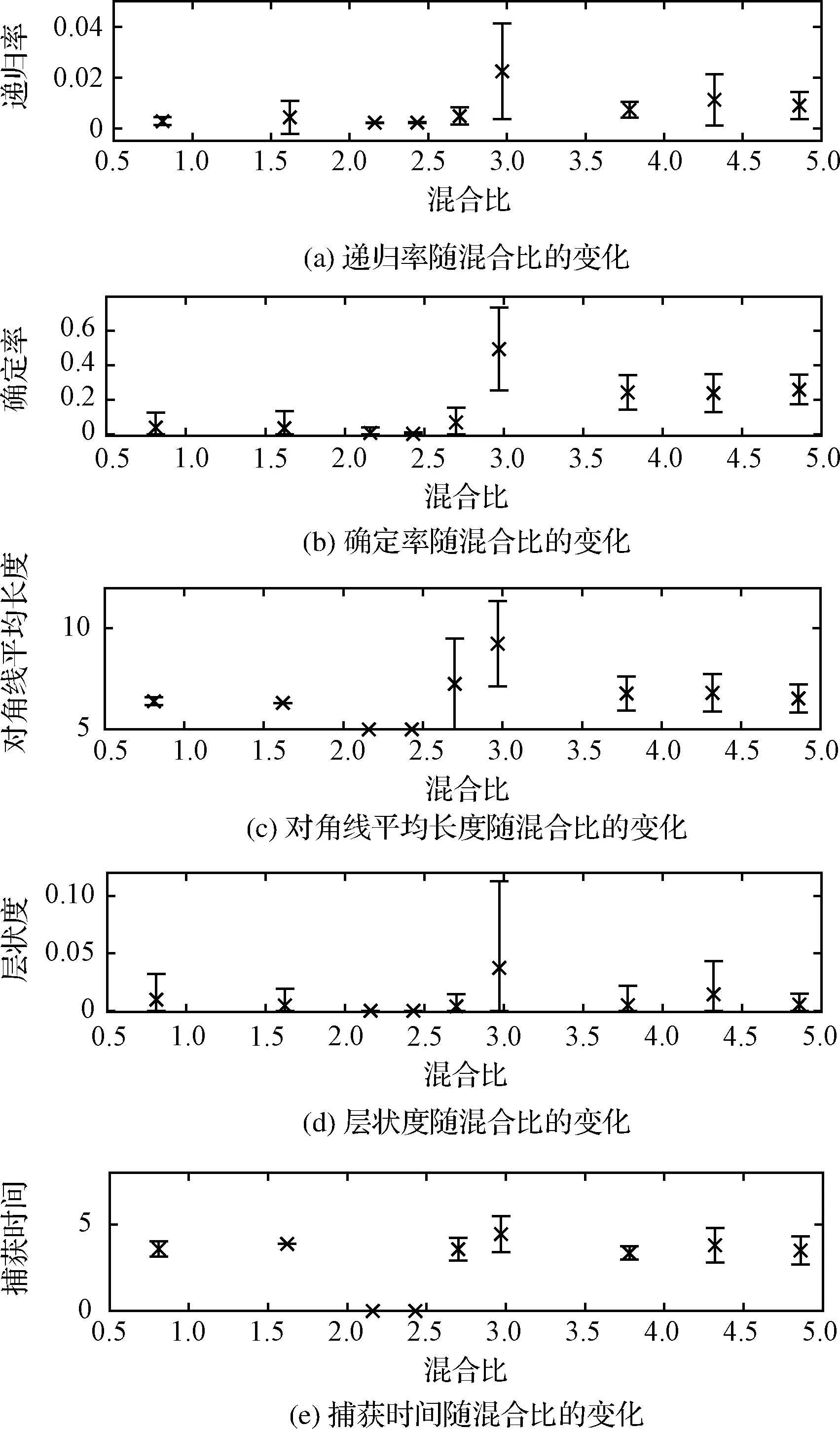
图10 递归量化指标随混合比的变化Fig.10 Variation of recurrence quantification analysis measures with mixture ratio

确定率中，混合比小于2.70时(燃烧噪声状态)确定率较低，从混合比2.70(阵发状态)开始逐渐增加，混合比2.97时(阵发状态)数值最大，继续增加混合比(准周期振荡状态)，确定率有所降低，但仍然比燃烧噪声阶段高一个数量级。说明确定率可以将阵发状态和准周期振荡状态与燃烧噪声状态区分出来。进一步，热声系统进入阵发状态(随后发生热声振荡)后，确定率数值显著增大，表明系统即将发生热声振荡，因此，可以用确定率对热声振荡进行预报。

对角线平均长度中，阵发状态时(混合比2.70，2.97)，数值较大，说明系统的周期性较强。准周期振荡状态(混合比大于2.97)时，对角线平均长度与燃烧噪声前两个工况(混合比0.81，1.62)数值接近，原因是准周期振荡会打断较长的对角线[21]，减低对角线平均长度。

层状度中，阵发状态(混合比2.97)数值较大，验证了层状度对阵发现象的识别能力[21]。捕获时间各工况下差别不大，说明各工况下局部点其动力学状态的持续时间相当。

4 结 论

采用递归方法对同轴离心式喷嘴燃烧稳定性进行了分析。获得了以下结果：

1) 试验中燃料流量不变，增加氧化剂流量，热声系统依次经历了燃烧噪声状态、阵发状态和准周期振荡状态。

2) 燃烧噪声状态和准周期振荡状态，相轨迹图均显示出无序状态；阵发状态时，相轨迹图在高幅值周期振荡和低幅值振荡之间连续转变。

3) 燃烧噪声状态，递归图呈现均匀分布特征。阵发状态时，递归图出现了黑色密度较大区域和白色区域交替的典型特征，进一步判断为第II类阵发现象，意味着系统发生了亚临界Hopf分叉，与前期实验结果一致。准周期振荡状态，递归图显示出与对角线平行的分段的短线。

4) 递归量化分析表明，确定率可以将阵发状态和准周期振荡状态与燃烧噪声状态区分出来，并可以对热声振荡进行预报。