“无”中生“有”
薛正桧
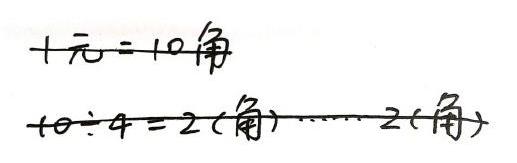
一、无疑处设疑
宋代理学家、教育家朱熹说:“读书无疑者,须教有疑,有疑者无疑,至此方是上进。”有了问题、疑问和惊奇,儿童才能积极主动地思考。伟大的物理学家爱因斯坦也告诫我们说:“提出一个问题往往比解决一个问题更重要。因为解决问题也许仅是一个数学上或实验室上的技能而已,而提出新的问题、新的可能性,从新的角度去看旧的问题,都需要有创造性的想象力,而且标志着科学的真正进步。”课堂中,学生能否产生实质性的问题,是学习是否真正发生的标志之一。
【片段一】
师:4个人到饭馆AA制吃饭,付了100元,找回3元。你能提出什么问题?
生1:每个人应付多少钱?
师:怎么解答?
生1:(100-3)÷4=24(元)……1(元),答:每个人付24元,还余1元。
师:这里面有“问题”吗?
(学生面面相觑。)
师:钱刚才是我出的,现在我收钱了,你准备给我多少钱?
生1:24元。
师:我好像不大认同,你就给我24元?
(生1迟疑。)
师:你到底给我多少钱?
生1:25元。
师:那你亏了。
生2:在24到25之间。
师:这种感觉挺好,既不是24元,也不是25元,应该比24元还多一点。过去我们学习有余数的除法时,算到这里就打住了。今天有事了,问题出在哪里呢?
生3:余下的1元,由谁出呢?
生4:1元能不能再4个人分?
师:请试一试。
【赏析】在学习小数除法之前,學生理解的除法是在整数范围内进行的,当除到被除数的个位不能整除时,那么就会用商和余数的综合形式来表示结果。在他们看来,“每个人付24元,还余1元”是一个再正常不过的结果了,没有任何可疑的地方。没有了疑问,产生不了问题,思维就不会展开。教师借助情境来还原现场“你准备给我多少钱”,让学生在具体的付钱活动中感知到问题的存在。原本学生认为“没事”,结果被教师“找出了事”“发现了问题”。付24元不对,付25元也不对。余下的“1元”究竟应该由谁来付?怎么付?学生已有的认知平衡被打破,他们认识到:最后的余数还得继续分下去,直至分完为止。一个新问题的产生,不知不觉地就将学生的视线拉向了更小的单位(角、分),“小数”呼之欲出,思维由此被激活,探究成了学生的内在需求。
二、无路处引路
近代教育家陶行知曾说:“教师之为教,不在全盘授予,而在相机诱导。”“凡为教,目的在于达到不需要教。”引导学生自己去发现问题,提出问题,并自主分析,解决问题,是教学的出发点,也是归宿。学生不是一个将要填满的容器,而是一支等待点燃的火把。只有把他们内在的学习动力、潜能激发出来,他们的成长才具有生命的意义,如种子一般生根,发芽,开花,结果。
【片段二】
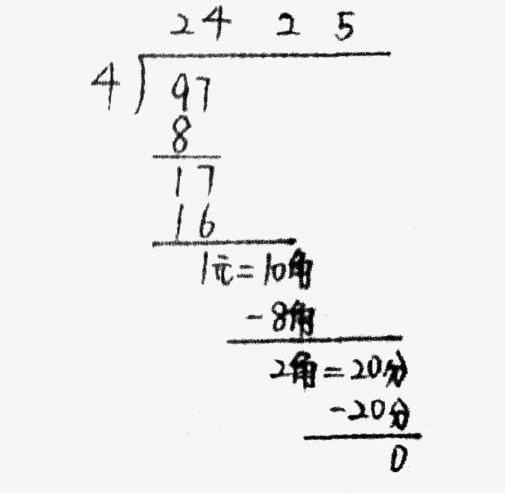
师:她(生1)写了半天,又划掉了(如下图)。谁懂她?
生2:她是把1元换成10角,10角除以4,每人2角,还是有余数,还是不好分。
生1:你理解我的意思。
师:你最懂她。先说这件事(把1元换成10角),我有没有告诉她?
生(众):没有。
师:(对着生1)特别巧,咱俩想到一块儿去了。这是10角,你来分一分。
(生1把10角分给4个人,每人2角,还剩2角。)
师:又出事了。出什么事了呢?
生1:剩下的不够分了。
师:所以这个时候,你怎么办?
生1:我把写的全划掉了。
师:那么这个2角怎么办呢?
生3:2角还可以换成20分。
生1:我知道了,20÷4=5(分),每人再分5分。
师:你特别想说什么?
生1:我想说,我遇到了困难没有去解决,不像这个同学遇到了困难就仔细去想,以后我也要这样。
师:做着做着出现了新问题,这个时候不要害怕,没关系,我们顺着这个思路慢慢去解决。
【赏析】一个学生在求解的过程中遇到了障碍,她本能地放弃了,她自认这不是一件光彩的事,想躲却没躲成,还被教师亮了相,多丢人啊!听课的教师也是一惊,为了成就教师的出彩而无视当事学生的感受,这不应该是有情怀的教师所为啊!可随着后续交流的开展,我们明白了教师的真正用意。把1元换成10角,这是重大的创举,教师大力表扬,先找她的“同盟军”,再把自己加进去说“咱俩想到一块儿去了”,并提供材料让她分一分,让她尽情享受成功的乐趣(虽然她先前没有意识到)。然后话锋一转,指出学生划掉答案的内在想法,并求助“这个2角怎么办呢”。经别人提醒后,学生迅速找到了下一步解题的方法。她明显感觉到这其实就是自己上一步方法的延续,1元不够分换成“角”,2角不够分再换成“分”,这种顿悟是何等珍贵啊!更为精彩的是,教师还让学生发表感想,“以后我也要这样”虽是只言片语,但影响深远。在这里,学习某个具体的知识不再是唯一目标,获得分析、解决所有问题的普适性策略成了至上追求。没事找事,跳出数学教数学,为学生的终身发展奠基,这是我们所有教育者都应具有的情怀。
三、无知时致知
对学生来说,学习数学的一个重要目的就是要学会数学思考。对教师来说,数学教学的思考应当从逻辑的、历史的、关系的等方面去展开,教给学生科学的思维方式与思维习惯,让学生去体悟数学的智慧与美。课堂中,当学生没能明晰知识的内涵时,我们要适时地“没事找事”,格物致知,让他们在已有问题解决的基础上提升认识。
【片段三】
师:每个人应付多少钱?
生(众):24元2角5分。
师:这里面还有事吗?解决了吗?
(学生面面相觑,似乎提不出问题了。)
师:那以后凡是花钱的事,我们就画一画、分一分,可以吗?
生1:不方便,麻烦。
师:这不就是事吗?学习之中总得有新的事!你们想怎么解决?
生2:把分的过程合在一个竖式里。
(学生根据整数除法列竖式的经验,补充成下图。)
师:看到这个竖式,你们有新的事吗?
生3:容易看成是“2425”元。
师:怎么办呢?
生(众):点上小数点。
师:点在哪儿呢?
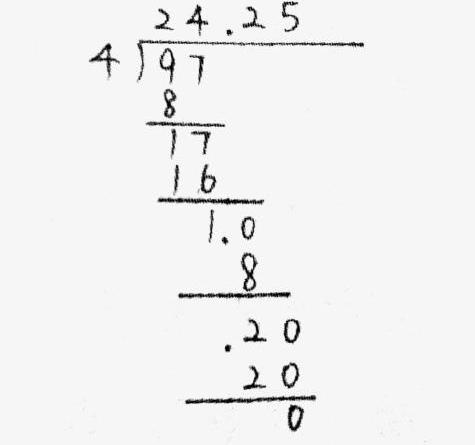
(学生根据元、角、分的意义把上图调整为下图。)
师:小数点为什么要点在这儿呢?
……
【赏析】从解决问题的角度看,当学生得出“24元2角5分”时,已经算是解决了问题。但这显然不是数学教学的真正目的,数学课不是为了解决问题而解决问题,而是以解决问题为载体,让学生在一系列的观察、探究、尝试、抽象、推理、验证等活动中,获得数学知识的扩充、能力的提升,以及素养的达成。数学是思维的体操,以形式化的符号语言呈现思维结果。算法是直观的,但算理却是抽象的,是高阶思维的集中体现,小数除法的计算最终必须落实到抽象的竖式之中。借助“元、角、分”情境,学生感悟到了“当有余数时,可以换成小一点儿的单位再继续除”,这是后续理性认识的基础。紧接着,教师引导学生从不同角度去反思。以后分钱,全部用操作(分、画)的方法吗?竖式中的结果会被当成整数,怎么办?竖式内部的小数点有没有必要加?没有了元、角、分,怎么思考97÷4?问题一个接着一个,在不断“找事”及解决问题的过程中,学生的思维一步步实现了由前运算到具体运算,再到形式运算的递进。
(作者单位:浙江省宁波滨海国际合作学校)

