基于灰色系统模型的辽宁省需水量预测研究

孟照宇

(辽宁省本溪市本溪县水务和移民事务服务中心，辽宁 本溪 117100)

0 引 言

水是维持社会发展和生产生活的基础性资源，预测与分析城市需水量具有重要的现实意义。经济发展和城镇化建设使得城镇用水量急剧增大，持续紧张的水资源矛盾对城镇健康发展构成严重威胁。所以，系统、全面的预测城市需水量十分必要，可为国民经济建设、供水系统建设和水资源合理规划配置等提供一定指导[1-2]。

当前，SD系统动力法、灰色理论法、回归分析模型和时间序列法等为最为常用的城市需水量分析法。其中，长时间序列的大量数据样本为序列分析法应用的重要条件，且通常存在较短的预测周期，因此对于中长期预测一般不适用；对于相关因素的选取，回归分析法往往受人为不确定因素的影响，同时各要素间的不同组合也会对预测结果产生较大偏差；系统动力学模型应考虑的相关数据和要素较多，且模型结构比较复杂、运算工作量大，研究人员的建模能力和专业知识在很大程度上决定了预测结果的可靠性。针对小样本、非线性和贫信息的评价灰色理论存在显著优势，在分析较短时间序列、不完全信息样本时具有较强适用性。灰色系统模型预测过程中虽然会受到环境因素的不利作用，但预测效果比较明显且精度相对较高。

受社会经济发展状况和自然资源条件双重制约的城市需水量预测，能够对预测结果产生影响的因素较多，且不同因素间通常存在密切的联系，这些因素所包含的信息有些未知、有些已知，即不确定和确定性因素两类，由此构成的需水量预测系统具有灰色属性。

1 灰色系统模型

1.1 理论分析

1982年邓聚龙建立了一种能够有效处理随机性问题的灰色系统模型，经过长期的发展现已形成较为完整的理论体系，并已广泛应用于能源、石油、工业、社会、农业、经济和地质等诸多科学领域，使得科学研究、生产生活等实际问题得以成功的解决，其应用成效和理论成果较为显著[3-4]。灰色系统模型是一种反映多因子之间强弱、大小、次序的数学方法，依据关联度大小描述比较序列隶属于参考序列的“紧密联系”程度，因具有要求样本数量少、运算量小、理论清晰等优点，可以有效避免数理统计法存在的不足，比较适用于需水量的预测分析[5-6]。另外，灰色关联法以历年实测数据为计算依据，由此获取的各要素值能够和预测结果保持较高的一致性。

针对系统信息少、结构体系不明确的情况，灰色系统理论能够从变量分析的角度给出新的解决思路和方法。根据各要素的关联性和测度寻找隐藏于系统内部的变化规律，通过运用映射处理法逐渐减少灰度，从而实现可知系统的处理，不断增加系统百度最终揭示系统的变化规律。变量在特定区间的变化灰色系统理论中参数的实质，通过弱化原始数据的随机性实现杂乱无章到规律性较强的转变，从而构造相应的模型。GM(1,1)模型为最常用的灰色预测方法，其可靠性与预测精度较高。

1.2 灰色GM(1,1)模型

预测过程中灰色GM(1,1)微分方程模型能够直接选用初始数据，删去不确定因素后累加形成灰色系统模型，从长时间序列中找出隐藏于上下波动数据的规律。新的数据序列呈指数变化趋势且规律性较为明显，对预测模型利用指数微分方程求解。根据下述流程搭建灰色GM(1,1)模型，具体为：

步骤一：设城市需水量预测原始数据序列为X(0)={X(0)(1),X(0)(2),…,X(0)(n),}，通过一次累加生成获取新的数据序列X(1)={X(1)(1),X(1)(2),…,X(1)(n),}，转化公式为：

X(1)(i)=∑X(0)(t),(t=1,2,…,i)

(1)

采用白化权函数和新的数据序列，建立微分形式的GM(1,1)方程模型如下：

(2)

式中：u、a为系统内生控制系数和系统发展变量。系统中参数u、a的运用利用最小二乘法确定，其表达式为：

(3)

其中：

时间响应函数为模型需水量预测的重要依据，数学表达为：

(4)

第(t+1)年累加的年度需水量预测值为以上模型求解的X(1)(t+1)值，进一步累减第(t+1)年年度需水量预测值可确定：

X(0)(t+1)=X(0)(t+1)-X(0)(t)

(5)

1.3 模型的检验

一般情况下，后验差方法为检验系统准确度的常用方法，其中小误差概率P和后验差比值C确定模型准确性的重要指标，具体如下：

C=S2/S1

(6)

(7)

(8)

P={|e(k)<0.6745S1|}

(9)

随着比值C的减小，模型的后验差精度和应用效果不断增强；模型应用效果随小误差概率P值的增大而增强，模型精度等级按照P和C的取值确定见表1。

表1 城市需水量预测精度等级

由于P和C的取值均可对模型总体精度产生作用，可利用如下公式确定精度，即：模型精度等级=Max{P所在等级，C所在等级}。

2 辽宁省需水量预测

根据灰色系统理论可认为GM(1,1)模型为指数模型，而原始数据的特点在很大程度上决定了模型预测效果。2010-2019年辽宁省农业、工业、生活和年总用水量数据波动较小，整体上呈平缓的单调变化特征，所以运用GM(1,1)模型预测需水量具有较强适用性；另外，状态变量因时间的不同而呈指数变化趋势，因此该模型不宜设置过长的预测周期。

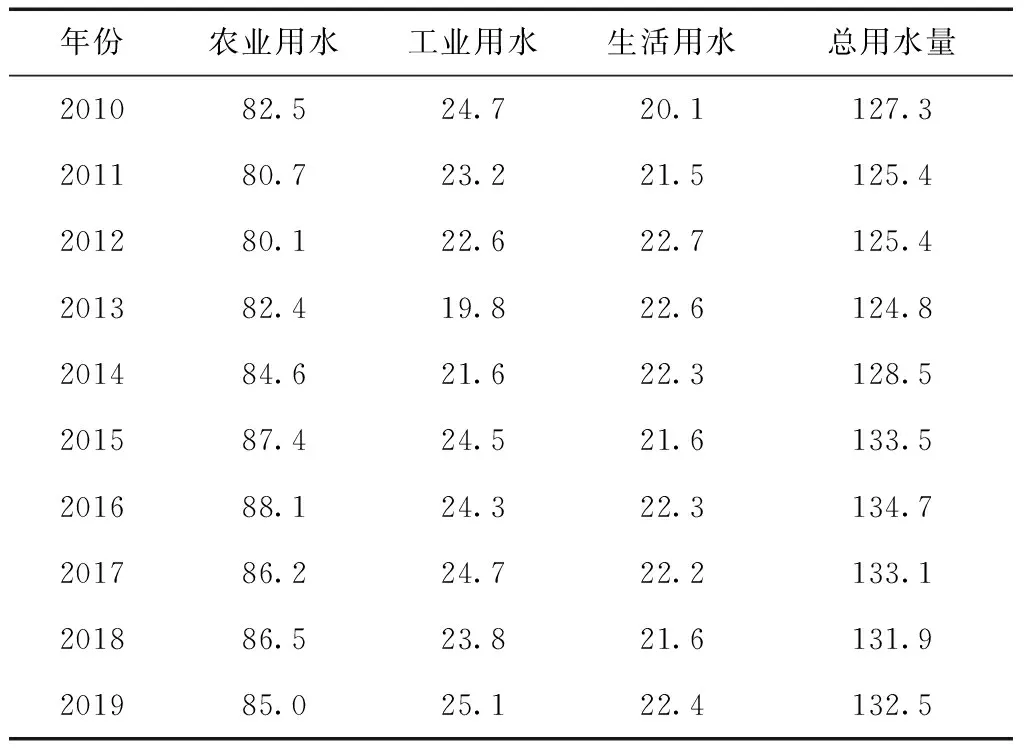
根据2020-2019历年用水量数据建立农业、工业、生活和总用水量灰色GM(1,1)模型，在此基础上预测分析2020-2028年用水量。统计整理2010-2019年历年用水量数据，见表2。

表2 2010-2019年历年用水量数据亿m3

年份农业用水工业用水生活用水总用水量201082.524.720.1127.3201180.723.221.5125.4201280.122.622.7125.4201382.419.822.6124.8201484.621.622.3128.5201587.424.521.6133.5201688.124.322.3134.7201786.224.722.2133.1201886.523.821.6131.9201985.025.122.4132.5

2.1 区域概况

辽宁省地处我国东北南部，东与韩国、日本隔海相望，隔鸭绿江与朝鲜相接，南临渤海、黄海，属于东北地区既沿边又沿海重要的多外开放门户。辽宁地区下辖沈阳、大连、抚顺、铁岭、朝阳、葫芦岛等14个地级市和2个省管县组成，总面积14.8万km2，狭长的海滨平原素有“辽西走廊”之称，地貌形态大致分为“六三一水三分田”。研究区为大陆性季风气候，年均气温为7.0℃-11.5℃，冬季少雨干暖，夏季气候凉爽，日照充足，年降水量600-1100mm。境内分布有饶阳河、大凌河、太子河、浑河、辽河等河流，各支流纵横交错、蜿蜒曲折，岛屿有大鹿岛、长兴岛、石城列岛及里长山列岛等266个，全省岛岸线长627km。由于复杂的气象条件和特殊的地理环境，降水量存在明显的季节性和区域性特征，每年的6-9月降雨较为集中且多暴雨或强降雨；空间尺度上，中部平原地区较高山低降水较少，与渤海相邻的东南部降水量充足，而西北部降水稀少且风沙干旱严重。该地区水资源利用以地下水为主，局部地区的地下水过度开采且水资源浪费严重；水资源边际效益低、可开发总量少、开采成本高；工矿产业及资源开发与工业用水基本匹配，境内水生态功能和水系统承载力呈下降趋势[7-11]。

2.2 建立模型

根据灰色系统理论建立农业、工业、生活和总用水量GM(1,1)预测模型，各行业用水量预测模型表达式如下：

1)结合灰色系统理论建立的总用水量预测模型为：

X(1)(t+1)=13023.15e0.002t-12937.4
X(0)(t+1)=X(1)(t+1)-X(1)(t)，t≥1
X(0)(1)=X(1)(1)=34.16

2)结合灰色系统理论建立的生活用水量预测模型为：

X(1)(t+1)=530.025e0.025t-522.305

X(0)(t+1)=X(1)(t+1)-X(1)(t)，t≥1

X(0)(1)=X(1)(1)=10.4

3)结合灰色系统理论建立的工业用水量预测模型为：

X(1)(t+1)=-116.268e-0.075t+124.745

X(0)(t+1)=X(1)(t+1)-X(1)(t)，t≥1

X(0)(1)=X(1)(1)=7.2

4)结合灰色系统理论建立的农业用水量预测模型为：

X(1)(t+1)=-500.186e-0.027t+515.710

X(0)(t+1)=X(1)(t+1)-X(1)(t)，t≥1

X(0)(1)=X(1)(1)=15.8

采用以上灰色GM(1,1)模型获取农业、工业、生活和总用水量预测拟合值，并确定各模型相对误差见表3。

表3灰色GM(1,1)模型预测值亿m3

年份农业用水相对误差工业用水相对误差生活用水相对误差总用水量相对误差201082.50 0.00%24.70 0.00%20.10 0.00%127.300.00 201180.18 -0.64%24.09 3.85%21.89 1.81%126.16-0.60 201280.06 -0.05%23.16 2.47%22.22 -2.10%125.44-0.03 201382.82 0.51%19.25 -2.76%22.62 0.08%124.690.09 201484.84 0.28%20.57 -4.75%22.29 -0.06%127.700.63 201587.32 -0.09%23.48 -4.18%21.38 -1.00%132.181.00 201687.61 -0.56%22.35 -8.01%22.79 2.18%132.751.47 201788.11 2.21%24.59 -0.44%22.17 -0.14%134.87-1.31 201886.45 -0.06%25.15 5.67%21.20 -1.84%132.80-0.68 201983.54 -1.72%27.42 9.24%22.63 1.03%133.59-0.82

2.3 模型的验证

采用后验差方法检验农业、工业、生活和总用水量的灰色GM(1,1)模型精度，结果发现各类主要用水和总用水量的小概率误差P和方差比C均呈良好效果，精度检测见表4。

表4 灰色GM(1,1)模型精度检验

根据表4检验结果可知，总用水量灰色GM(1,1)模型存在最大的方差比值C，检验结果为“合格”且模型精度相对较差，预测结果和区域实际情况存在偏差。通过分析原因发现，各种节水技术的推广与发展、第三产业状况、生活水平、经济发展以及人口变化等因素均可在一定程度上影响总用水量产生，研究期间呈波动增长趋势。较其它模型而言，农业用水灰色GM(1,1)模型存在最小的方差比值C，该模型的检验结果为“好”且检验精度最高。进一步分析原因可知，辽宁地区水资源系统对农业灌溉供给较为稳定，水利设施建设较为完善、成熟，因此可以比较准确的预测出未来用水变化情况，保证了目标年份用水预测的准确性和可靠性。

2.4 需水量预测

采用农业、工业、生活和总用水量的灰色GM(1,1)预测模型，预测分析辽宁地区2020-2028年农业、工业、生活和总需水量，见表5。

表5 2020-2028年用水量预测值亿m3

年份农业用水工业用水生活用水总用水量202085.2125.522.36133.07202185.8725.322.57133.74202285.9025.823.12134.82202386.0426.223.07135.31202486.3626.623.65136.61202586.2526.524.14136.89202687.0127.224.02138.23202787.4427.524.26139.20202887.3828.024.35139.73

根据表5可知，辽宁省总需水量2020-2028年呈缓慢增长趋势，该预测结果与辽宁地区水资源鬼狐目标保持较高的一致性。增长空间较大的为生活用水量，而农业和工业需水量则表现出下降趋势，该变化结果与区域发展战略及产业布局基本相符。

4 结 论

结合水资源预测的复杂性、不确定性和区域性特征，考虑2010-2019年辽宁身农业、工业、生活、总用水量历年统计资料和灰色系统理论，建立具有较好拟合度的GM(1,1)预测模型，可为各主要用水及总需水量的预测提供一种新的的技术手段。对2020-2028年辽宁省需水量利用建立的灰色GM(1,1)模型预测，结果发现各区域需水量呈缓慢增大趋势，其中增长空间较大的为生活用水量，而农业和工业需水量则表现出下降趋势。各行业需水量预测值与辽宁地区水资源发展战略、产业布局及总体规划目标保持较高一致性，能够基本体现辽宁地区的未来用水量变化特征。对城市需水量状况利用灰色GM(1,1)模型预测，可为区域水源管理规划和水资源持续利用提供科学指导。