腐蚀对风车联合作用下斜拉桥拉索疲劳可靠性的影响分析

李岩 ，杨婷婷 ，夏梁钟

（1.哈尔滨工业大学交通科学与工程学院，黑龙江哈尔滨150090；2.哈尔滨工业大学土木工程学院，黑龙江哈尔滨150090；3.广西交通设计集团有限公司，广西 南宁530000）

斜拉索作为斜拉桥的关键构件，运营期承受车辆和风荷载等反复作用，其疲劳问题一直广受关注.环境和人为因素的影响可造成拉索系统发生腐蚀，进而造成其抗疲劳性能退化[1-4].国内外有关拉索腐蚀和疲劳性能评价等问题已开展了一些研究工作.徐俊结合实际斜拉索检测数据，建立了钢丝锈蚀程度八等级分级标准[2]；徐阳通过人工加速腐蚀试验，利用腐蚀因子描述了高强钢丝均匀腐蚀与点腐蚀间的关系，建立了高强钢丝腐蚀退化的预测模型[3]；侯金生对某大桥换下的腐蚀拉索进行疲劳试验，建立了腐蚀拉索S-N曲线时变退化模型[5]；兰成明等研究提出钢丝疲劳寿命的多参数Weibull模型，分析了斜拉索疲劳寿命与其内部钢丝疲劳寿命及断丝率的关系[6]；Faber等指出平行钢丝拉索疲劳寿命服从Weibull分布，并根据贝叶斯理论更新了平行钢丝的疲劳寿命评估模型[7]；Matteo等从服役斜拉桥更换下的拉索中获取钢丝样本，进行力学性能测试来评估服役阶段索结构的可靠指标[8]；Cremona等基于Monte-Carlo法建立了拉索可靠性评估模型[9]；Maljaars等考虑拉索初始缺陷，基于断裂力学方法提出一种评估拉索抗力的概率模型，依托工程实例进行了斜拉索的疲劳失效分析[10]；Álvarez等对一座服役25年的多塔斜拉桥拉索退化过程进行分析，结果表明腐蚀可导致拉索疲劳寿命大幅下降[11].目前针对在役桥梁斜拉索的疲劳可靠性预测和评定研究中，腐蚀因素影响还少有考虑.不同腐蚀状况对运营斜拉桥拉索的疲劳可靠性影响规律尚不明晰，难以为在役桥梁斜拉索的疲劳评估和状态预测提供必要的依据和理论基础.

为此，本文在随机车辆-风-桥梁系统动力响应分析理论框架下，结合既有研究的人工加速腐蚀高强钢丝疲劳性能试验结果，建立了考虑腐蚀影响的运营环境下斜拉索疲劳可靠度分析方法.依托算例开展腐蚀对运营环境下斜拉桥拉索疲劳可靠性的影响研究，可为在役斜拉桥拉索的疲劳寿命评价和安全评估提供参考.

1 考虑腐蚀的拉索疲劳抗力模型

1.1 人工加速腐蚀高强钢丝的疲劳性能

依据拉索常用镀锌高强度钢丝试件的人工加速腐蚀试验结果[3，12]，通过对不同人工加速腐蚀时长的钢丝样本表观状况与腐蚀分级特征描述[2]的比对分析，得到试验样本钢丝腐蚀等级如下：1 d-腐蚀等级Ⅰ；7 d-腐蚀等级Ⅱ；10 d-腐蚀等级Ⅲ；30 d-腐蚀等级Ⅳ；60 d-腐蚀等级Ⅴ.选取腐蚀暴露时间为1 d、7 d、10 d、30 d和60 d的腐蚀钢丝进行4种应力水平（0.4～0.8 σu、0.3～0.6 σu、0.25～0.5 σu和 0.2～0.4 σu，σu=1 670 MPa为极限强度，应力比为0.5）的疲劳强度试验.该试验采用先对钢丝预腐蚀，后进行疲劳试验的拉索腐蚀疲劳常用试验方法，未考虑应力与腐蚀的交互作用.基于试验结果，拟合得到上述5种不同腐蚀程度钢丝的疲劳寿命曲线.

既有研究结果表明平行钢丝斜拉索的高强钢丝和拉索的S-N曲线斜率相同，且当概率保证率为99.7%时，拉索疲劳寿命大于钢丝疲劳寿命，设计疲劳寿命200万次的研究结果类似[3，6].同时，拉索疲劳寿命主要由组成拉索的一小部分疲劳寿命最短钢丝控制.考虑到实际运营环境中的拉索腐蚀并不是均匀发生的，一般按照腐蚀程度最为严重的部分钢丝状况确定等级[2].为此，本研究偏安全的基于前述腐蚀钢丝疲劳试验结果，将腐蚀钢丝与拉索的疲劳寿命曲线等效，得到不同腐蚀等级的拉索（对应不同加速腐蚀周期）的S-N曲线方程如下：

上述腐蚀和疲劳试验过程和相关数据可参考文献[13]，此不赘述.目前工程设计中对于斜拉索一般以考虑安全系数的设计荷载（如车辆活载等）下通过200万次等效加载循环作为评价其疲劳性能的标准.相关研究引用最为广泛的是美国后张法学会斜拉桥委员会基于大量试验数据给出的拉索疲劳设计准则，其中平行钢丝拉索200万次加载循环的疲劳应力幅设计值为144.8 MPa，并指出任何超过20.69 MPa的受拉应力幅应计入[14].同时，拉索疲劳试验研究受时间和条件等限制，对于循环次数远大于200万次的低应力幅疲劳试验很少开展.各国学者开展的斜拉桥拉索疲劳损伤相关研究，均以既有试验研究数据拟合得到S-N曲线，进行桥梁使用荷载下的疲劳寿命或可靠性分析[15-18].

1.2 加速腐蚀与实际服役的时间尺度转化

斜拉索内部高强钢丝受外界环境等因素影响发生腐蚀后，其腐蚀状况将随运营时间的增长不断恶化[6].时变腐蚀对拉索疲劳性能的影响，可通过对拉索S-N曲线进行时变更新来描述.本文以前述试验数据为基础，建立加速腐蚀时间与实际服役时间的关系，进而拟合得到拉索S-N曲线参数与实际服役时间之间的关系，建立时变腐蚀拉索S-N曲线退化模型.

由前述加速腐蚀试验数据，得到加速腐蚀条件下钢丝均匀腐蚀深度随时间变化规律如图1所示[13].

图1 均匀腐蚀深度随时间的变化规律Fig.1 Uniform corrosion depth variation with time

由图1可知，在人工加速腐蚀试验中，钢丝腐蚀速率的转折点将钢丝腐蚀分成了2个阶段：仅镀锌层腐蚀阶段和内部高强钢丝腐蚀阶段.2个阶段的转折点在第7天.拉索高强钢丝均匀腐蚀的2个阶段可用式（2）表示：

式中：ψ1和ψ2分别表示镀锌层和钢的腐蚀速率；γ1和γ2为模型参数；tc为腐蚀转折时间点；du，Zn（t）和du，Fe（t）分别表示高强钢丝镀锌层和内部钢丝的均匀腐蚀深度.各系数回归值如式（3）所示：

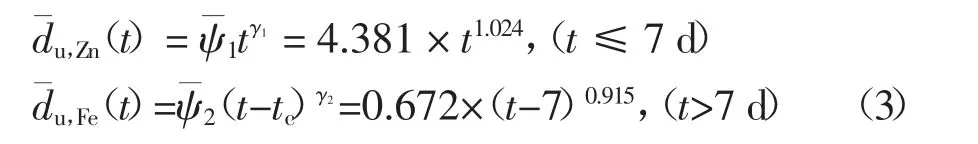
当人工加速腐蚀试验与实际服役环境腐蚀导致的均匀腐蚀深度相同时，可认为加速腐蚀钢丝与对应的实际服役环境腐蚀下钢丝的腐蚀程度相当.实际斜拉桥由于服役腐蚀环境差异，其斜拉索的腐蚀速率不同.通过均匀腐蚀深度等效原则，可建立人工加速腐蚀时间尺度与实际服役时间尺度的关系.现以南京三桥为例，按照以上等效原则，建立人工加速腐蚀与实际服役时间尺度的关系.该桥位于工业区，根据曹楚南等[19]对该区域自然环境下高强镀锌钢丝腐蚀试验的研究结果，发现高强钢丝24 μm厚度的镀锌层全部腐蚀消耗需3.9年.此时，钢丝处于第一腐蚀阶段，据此有如下换算：

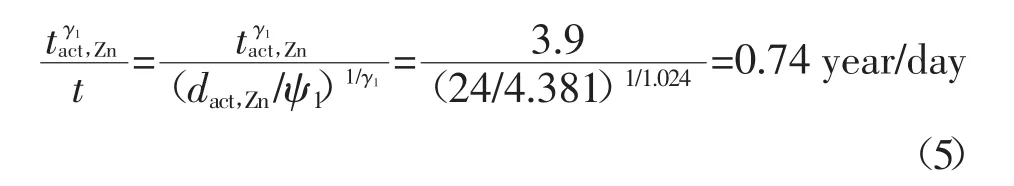
由此可知钢丝腐蚀阶段，盐雾试验条件下1 d相当于在该桥所在地区自然条件环境腐蚀0.74年的腐蚀程度.其中盐雾试验条件为：盐雾NaCl溶液浓度（5±0.5）%，pH 值 3.0～3.1，室内温度为（35±2）℃.

虽然当斜拉桥处于不同桥址环境中时，斜拉索受到环境腐蚀的影响程度不同，但采用均匀腐蚀深度等效原则建立人工加速腐蚀试验时间尺度与实际服役环境时间尺度的换算公式的方法具有通用性[20].

1.3 考虑时变腐蚀的拉索S-N曲线

研究以前述高强钢丝加速腐蚀试验结果为基础，建立拉索时变腐蚀的疲劳退化模型.

首先，为了便于采用公式（1），将拉索S-N曲线方程NSm=C写成对数形式：

式中：A=lg C，B=m，m和C是与材料性能及构件构造细节有关的常数.

根据高强钢丝加速腐蚀试件疲劳试验得到的S-N曲线方程（1），并将试验的时间尺度，按照方程（5）转化至实际环境服役时间尺度，通过最小二乘法拟合得到参数时变腐蚀拉索S-N曲线的参数A、B随时间变化关系，时变曲线如图2所示.

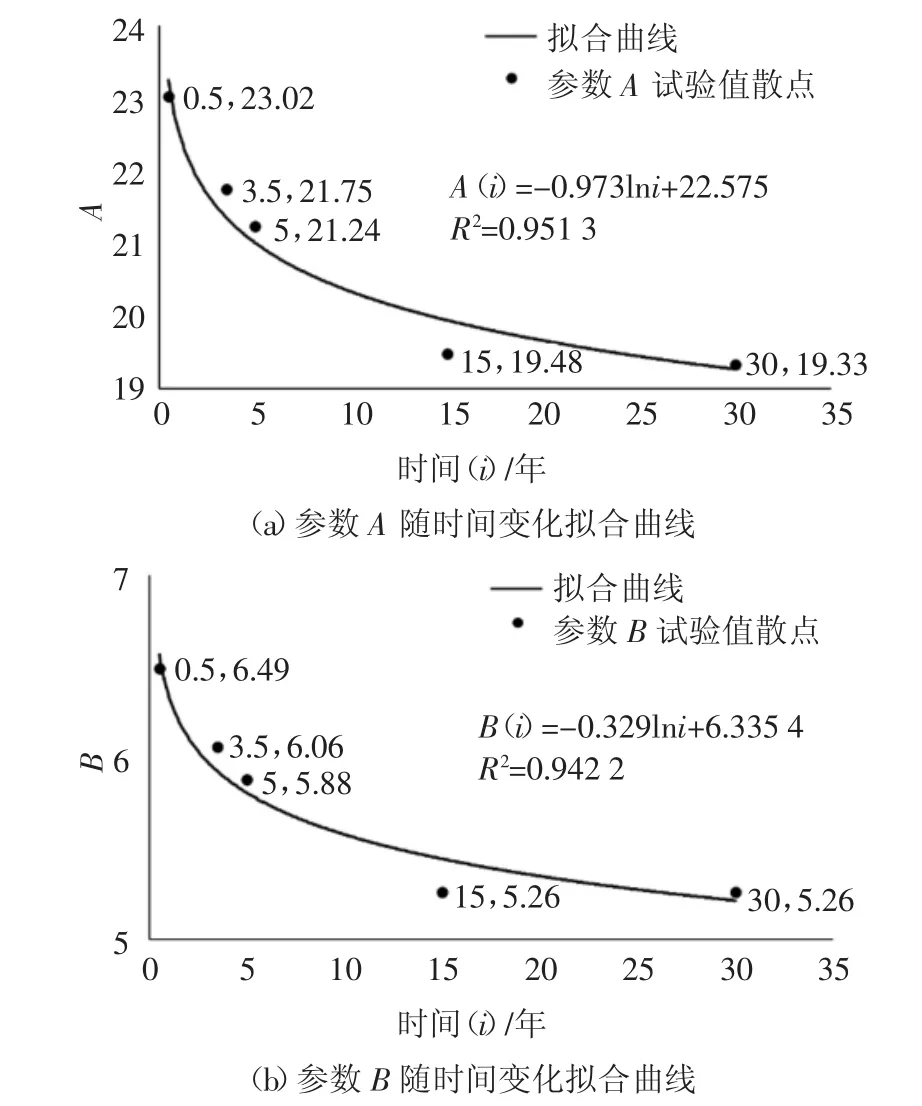
图2 时变腐蚀条件下拉索S-N方程参数时变曲线Fig.2 Time-varying parameters of S-N curves under different corrosion periods

由此得到时变腐蚀条件下拉索S-N曲线参数A、B的时变表达式：

其中i为桥梁服役时间长度（年）.据此得到桥梁服役期内考虑腐蚀的拉索时变S-N曲线为：

2 考虑腐蚀影响的斜拉索疲劳可靠性分析方法

2.1 考虑腐蚀影响的拉索疲劳可靠性分析模型

在随机荷载作用下拉索内部损伤逐渐累积，导致拉索疲劳破坏，采用线性疲劳累积损伤模型可以得到拉索的安全余量方程为：

式中：D（n）和Dc分别为累积损伤和临界损伤，均为随机变量.拉索的疲劳可靠度Ps可表示为：

2.1.1 腐蚀分级条件下拉索疲劳可靠性分析模型

按照Miner线性累积损伤准则，随机荷载下拉索的疲劳损伤可描述为：

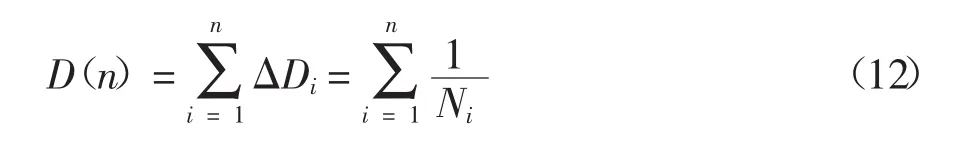
其中ΔDi是第i级应力幅造成的损伤.考虑到服役期内拉索承受连续变化的循环应力幅作用，将拉索SN方程代入式（12），可得：

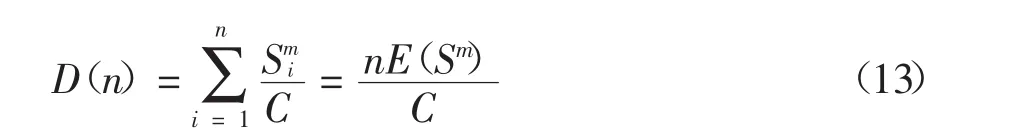
其中E（·）代表数学期望，则疲劳极限状态方程变为：

按照线性累积损伤等效原则，变幅应力对应的等效应力幅的计算公式如式（15）：

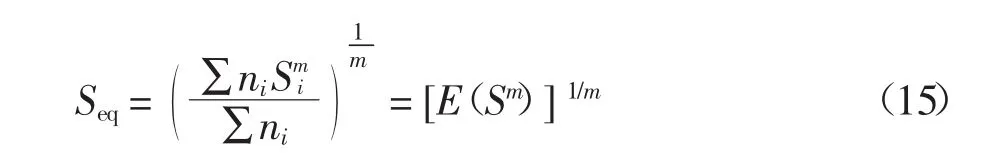
其中Seq为等效应力幅，其随机分布类型由统计获得.将式（15）代入式（14），疲劳极限状态方程变为：

其中材料性能参数C可通过不同腐蚀等级下的拉索S-N曲线获得，临界损伤Dc服从对数正态分布[21].通过应力谱的模拟计算以及Seq的统计分析来描述交通和风荷载的随机性.首先通过模拟计算得到多个典型时间块的拉索应力时程，经雨流法计数处理后获得应力幅及其循环次数；然后分析得到各时段的等效应力幅，并统计分析得到各典型时间段的等效应力幅；最后拟合得到等效应力幅的随机分布类型和参数.

2.1.2 腐蚀分级条件下拉索疲劳可靠性分析模型

将时变腐蚀拉索的S-N曲线方程（9）代入到拉索疲劳极限状态方程（16），可得运营年限为Ns时的拉索疲劳极限状态方程如下：

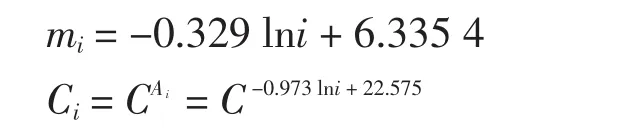
2.2 疲劳可靠度计算过程和步骤

图3给出了基于Monte-Carlo法考虑腐蚀的随机车辆与风载联合作用下的斜拉索疲劳可靠度计算过程，篇幅所限，详细步骤未予赘述，具体可见文献[22].在此仅对拉索等效应力幅的计算过程予以简要说明：1）按照交通调查确定车型、车重、车间距和横向位置随机分布模型，进行随机车辆模拟，获得典型时间块内随机交通荷载样本；2）按照桥址处风荷载统计数据和概率分布拟合结果确定极值风速、平均风速和风向服从的概率分布，开展风速、风向和脉动风时程样本模拟；3）基于数值模拟分析程序计算典型时间块内拉索的动力响应时程；4）考虑车辆和风荷载随机性，对各样本典型时间块拉索应力时程进行应力幅和循环次数统计.基于线性累积损伤等效准则，以循环次数为常量，由式（15）分别计算得到多个等效应力幅样本；5）对多个等效应力幅样本进行统计分析，获得其服从概率分布及参数.

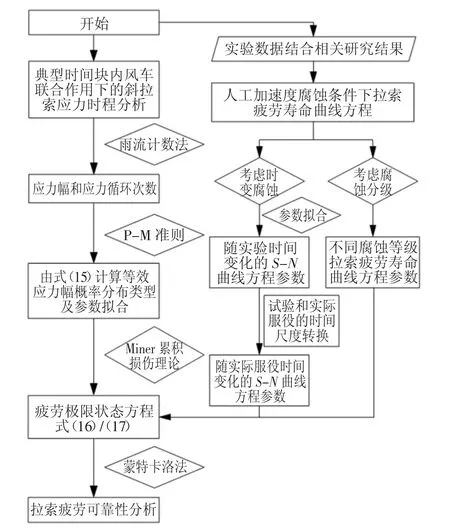
图3 考虑腐蚀影响的斜拉索疲劳可靠度分析流程Fig.3 Flow chart of fatigue reliability analysis for cable considering the corrosion

3 腐蚀因素对运营条件下斜拉索疲劳可靠性的影响分析

3.1 拉索应力谱分析

依托南京二桥南汊主桥作为工程背景开展研究，该桥共有80对斜拉索，桥型立面布置如图4所示.

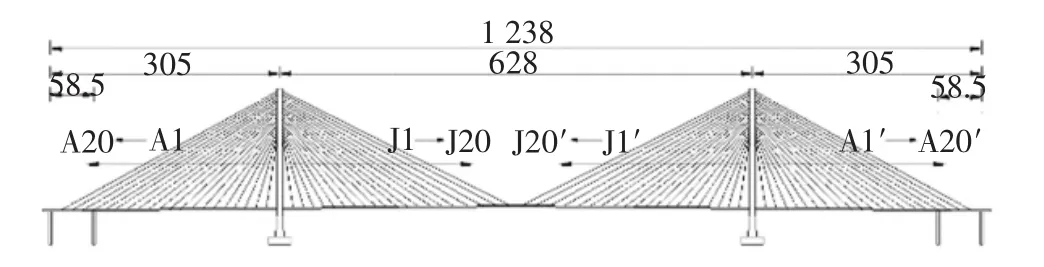
图4 桥梁立面布置（单位：mm）Fig.4 Bridge elevation（unit：mm）

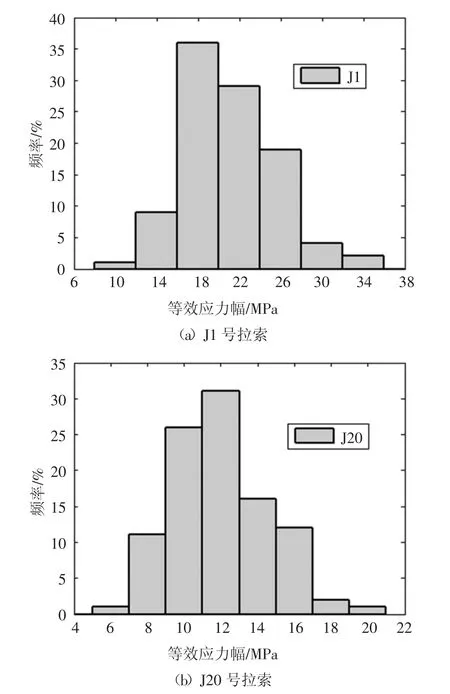
图5 拉索等效应力幅分布直方图Fig.5 Equivalent stress amplitude distributions of cables

大桥随机风载和交通荷载谱的模拟实现过程及相关结果详见文献[22].通过自行开发的大跨桥梁风车桥动力分析程序，对桥例进行了不同风速下随机车流与桥梁耦合振动响应分析.考虑交通量增长的随机车载和风载联合作用下的拉索应力谱计算、等效应力幅概率统计分析具体实现过程和结果详见文献[22].以大桥建成第一年为例，按照2.2节所述流程，计算得到J1和J20号拉索的等效应力幅最大值分别为34 MPa和20 MPa（如图5所示）.在此有必要对导致等效应力幅较小的原因进行解释：考虑典型时间块内的随机风载作用后，拉索实际变幅应力幅循环的次数较单独交通荷载作用情况发生了几何数量级水平的大幅度增加，且包含较大比例的低阶应力幅.本文等效应力幅按应力循环次数不变的方式计算得到，由此导致统计得到的等效应力幅幅值较小.拉索实际存在一定比例的大应力幅，如J20拉索最大应力幅可达165.8 MPa，篇幅所限，应力时程未列出，具体可参考文献[22].

3.2 疲劳分析参数的确定

根据式（16）（17）建立拉索的疲劳极限状态方程，采用Monte-Carlo法分析拉索疲劳可靠度.将可靠性分析中涉及的随机变量列于表1.拉索S-N曲线中的参数m和C为非随机变量，分别按照前述腐蚀分级和时变腐蚀模型表达式（1）（7）（8）确定，随交通量的增长，应力幅循环次数n也随之改变，等效应力幅的均值和方差由统计分析得到.

表1 随机变量Tab.1 Stochastic variable

3.3 考虑腐蚀分级的拉索疲劳可靠性分析

首先以运营10年为例，分析得到随机交通与风荷载联合作用下全桥拉索疲劳可靠度（如图6所示）.由图6可知拉索疲劳可靠度分布并不均匀，可靠度较低的拉索主要为江侧J5～J10和岸侧A5～A8范围（拉索编号见图4），最低为A6号拉索.为此后继考虑腐蚀影响的拉索疲劳可靠性分析以A6号拉索为对象进行.

图6 运营10年后全桥斜拉索疲劳可靠度Fig.6 Fatigue reliability of all the cables after 10 years

南京二桥与前述南京三桥所处环境基本相同，可认为前文已建立的人工加速腐蚀试验与实际服役环境时间尺度的换算公式（5）及参数适用于本桥.

据实际交通观测和交通量增长预测模型[23]，考虑过桥交通量的增长影响，以A6号拉索为例，基于前述分析方法得到其在不同腐蚀等级下的动态疲劳可靠度如图7所示（假定腐蚀等级I级与无腐蚀条件相当）.可见随服役时间增加，各腐蚀等级的拉索疲劳可靠指标均不断下降，且下降速度在前期（前25年内）明显大于后继使用期（25年到100年）.在桥梁运营初期，随腐蚀等级的恶化，拉索疲劳可靠指标下降速度变快.以V级腐蚀为例，使用期前25年内拉索动态疲劳可靠指标合计下降21.8%，下降速率为0.87%/年，为完好状况下降速率的1.42倍；使用期后75年，拉索可靠指标下降了11.3%，下降速率为0.15%/年，为完好状况下降速率的1.63倍.

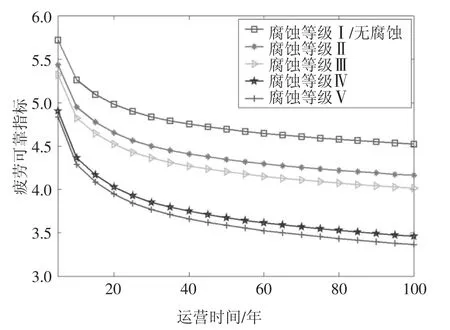
图7 不同腐蚀等级下A6拉索时变疲劳可靠度的比较Fig.7 Comparison of time varying fatigue reliability under different corrosion level for the cable A6

为进一步分析设计使用期内不同腐蚀等级下拉索的疲劳可靠指标差异情况，将不同腐蚀状况下A6号拉索动态疲劳可靠指标进行相邻等级差值处理，结果如图8所示.可见，腐蚀等级Ⅱ级和Ⅲ级、及Ⅳ级和Ⅴ级间的拉索疲劳可靠指标差值相对最小，变化范围在0.1～0.15之间.导致该现象的原因为Ⅱ级和Ⅲ级腐蚀时拉索内部高强钢丝都处于镀锌层腐蚀阶段；Ⅳ级和Ⅴ级则都处于拉索内部高强钢丝受腐蚀阶段.腐蚀等级Ⅰ级和Ⅱ级间的可靠指标差值变化范围在0.29～0.36间，该差值主要是由于Ⅱ级腐蚀时高强钢丝锌层开始腐蚀所致；腐蚀等级Ⅲ级与Ⅳ级的可靠指标差值处于0.41～0.55之间，相对变化最为显著，这是由于Ⅲ级与Ⅳ级正处在锌层腐蚀与高强钢丝腐蚀的过渡阶段，当内部高强钢丝开始腐蚀时导致了拉索的疲劳可靠指标明显降低.

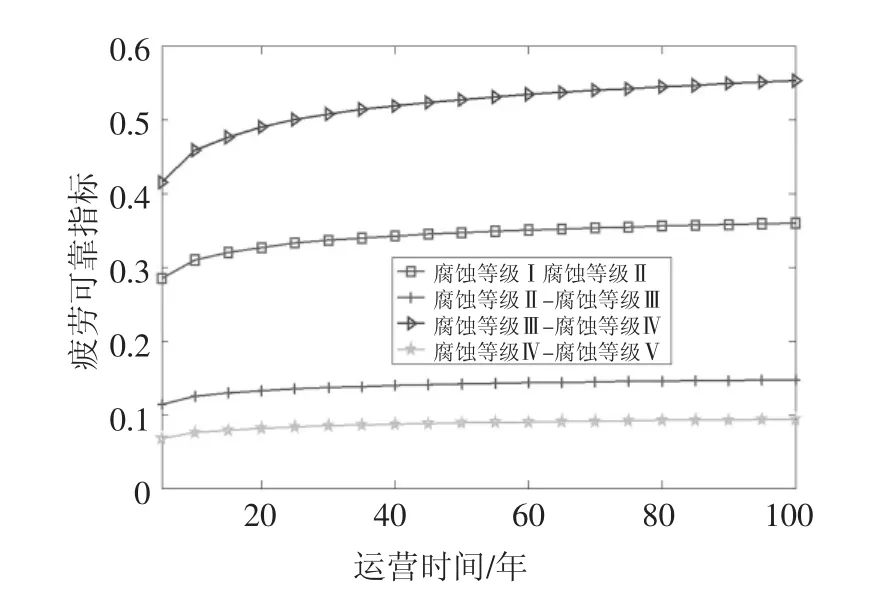
图8 相邻腐蚀等级间A6拉索时变疲劳可靠指标差值Fig.8 Change values analysis of fatigue reliability index between the adjacent corrosion levels for the cable A6

为考察腐蚀等级对全桥拉索疲劳可靠度的影响规律，以服役期10年为例进行了拉索疲劳可靠度分析，结果如图9所示.可见随腐蚀等级提高，全桥拉索的疲劳可靠指标均呈明显下降趋势，其中可靠指标最低的为A6号拉索，腐蚀Ⅴ级相对Ⅰ级条件下其可靠指标下降了19.6%.

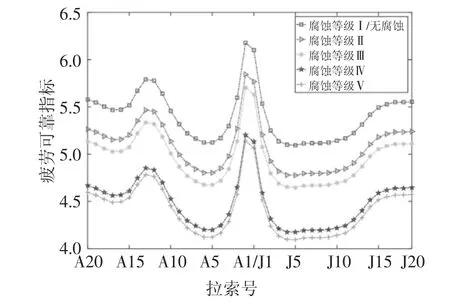
图9 不同腐蚀等级下全桥拉索疲劳可靠指标分布Fig.9 Fatigue reliability index of the cables under different corrosion levels

为进一步研究腐蚀等级对拉索疲劳寿命的影响，选取目标可靠指标为3.5[23]，进行了全桥拉索疲劳可靠寿命预测分析，结果如图10所示.

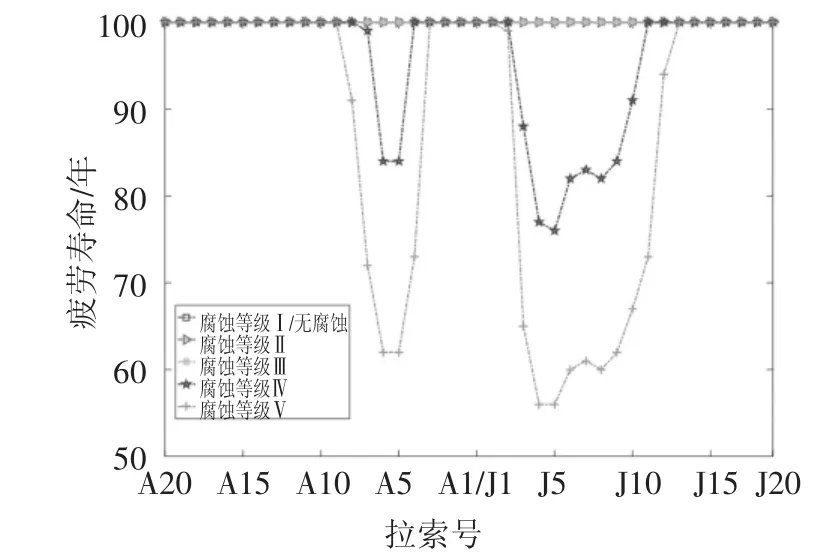
图10 不同腐蚀等级下全桥拉索疲劳寿命预测Fig.10 Fatigue reliability life of cables under different corrosion levels

由图10可知，腐蚀等级Ⅰ、Ⅱ和Ⅲ条件下，目标可靠指标全桥拉索疲劳寿命均可达到100年；当腐蚀等级达到Ⅳ级以上时，腐蚀对中等长度拉索疲劳寿命影响较大；当腐蚀程度达到Ⅳ级时，全桥拉索疲劳寿命较无腐蚀的降幅为1%～24%；腐蚀等级为Ⅴ级时，全桥拉索疲劳寿命降幅为1%～44%.

3.4 考虑时变腐蚀的拉索疲劳可靠性分析

实际斜拉桥拉索发生腐蚀后，腐蚀会由于环境和荷载等因素的影响逐步发展，其过程可通过前述建立的拉索时变腐蚀疲劳模型进行描述.为研究时变腐蚀对拉索疲劳可靠性的影响，针对桥例在时变腐蚀、不同腐蚀等级和无腐蚀条件下拉索的动态疲劳可靠指标进行分析，并以A6号拉索为例给出分析结果（如图11所示）.发现时变腐蚀影响下（假定腐蚀从桥梁通车运营开始），前25年内拉索的疲劳可靠指标下降了41.9%，降幅速率为1.68%/年，其疲劳可靠指标降幅及其速率分别为腐蚀Ⅰ级到Ⅴ级的2.74倍、2.46倍、2.35倍、1.98倍和1.43倍.服役期第25年至100年，时变腐蚀拉索的可靠指标下降了46.9%，降幅速率为0.63%/年，降幅及其速率分别为腐蚀I级到V级的6.80倍、5.90倍、5.54倍、4.33倍和4.14倍.

图11 时变腐蚀与不同腐蚀等级下A6拉索疲劳可靠度比较Fig.11 Comparison of fatigue reliabilities under time varying and different corrosion levels for the cable A6

综上所述，拉索腐蚀一旦发生，如不及时采取必要的维修和补救措施，则在时变腐蚀影响下拉索的疲劳可靠指标将迅速下降，其下降幅度和速度较仅考虑腐蚀分级更为明显，时变腐蚀导致的拉索损伤积累速率相比于腐蚀程度不变的情况增长更快，进而造成拉索疲劳可靠寿命急剧下降.因此在实际工程中及时在早期发现拉索腐蚀病害并进行及时处理，采取有效措施避免腐蚀恶化或有效减缓其发展，是保证拉索安全和延长其使用寿命的关键.

斜拉索运营期的维护质量也是显著影响拉索疲劳可靠寿命的重要因素.现以桥例拉索受到腐蚀影响的起始时间分别为运营10年、15年和20年后为例，分析时变腐蚀模型下腐蚀开始时间对拉索动态疲劳可靠性的影响.以A6号拉索为例，分析结果如图12所示.目标可靠指标为3.5条件下，腐蚀开始时间为运营10年、15年和20年的拉索疲劳可靠寿命分别为13年、18年、38年；腐蚀发生后仍可安全运营的时间分别为3年、5年、18年.可见，腐蚀发生时间越早，拉索的疲劳可靠性下降越快.

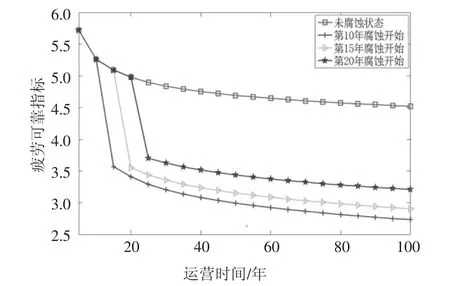
图12 腐蚀开始时间对A6拉索时变疲劳可靠指标的影响Fig.12 Influence of start time of corrosion on fatigue reliability index for the cable A6

因此，在既有桥梁的斜拉索腐蚀检测与寿命评估中，应考虑腐蚀开始时间的影响，以便更为合理地估计拉索的安全使用寿命，科学选择拉索的维护或更换处置方案，提高维护经济性.

5 结论

1）基于拉索高强钢丝的加速腐蚀试验和疲劳试验，并结合既有的相关研究结果，提出了考虑腐蚀的斜拉索疲劳抗力模型，建立了考虑腐蚀影响的斜拉索疲劳可靠度分析方法，可为在役斜拉桥的拉索疲劳寿命评估提供基础和借鉴.

2）拉索动态疲劳可靠指标的下降速率随腐蚀等级提高而增大，且运营初期下降速度远大于后期；腐蚀程度为Ⅰ级和Ⅱ级时，腐蚀对拉索疲劳可靠寿命的影响较小；当腐蚀等级达到Ⅲ级及以上时，对拉索疲劳寿命影响明显，尤其对靠近桥塔及辅助墩处拉索的影响最大，其中Ⅳ级和Ⅴ级腐蚀时，拉索疲劳寿命较无腐蚀状况的降幅最大分别达24%和44%.

3）相邻腐蚀等级下拉索动态疲劳可靠指标的变化程度分析表明：腐蚀Ⅱ级和Ⅲ级、Ⅳ级和Ⅴ级间的疲劳可靠指标变化幅度最小（0.1～0.15），腐蚀I级和Ⅱ级的可靠指标变化幅度较大（0.29～0.36），腐蚀Ⅲ级与Ⅳ级的可靠指标变化幅度最大（0.41～0.55）；相邻腐蚀等级处于不同的腐蚀阶段（锌层腐蚀阶段与高强钢丝内部腐蚀阶段）是导致其对应的拉索疲劳可靠指标产生显著变化的主要原因.

4）时变腐蚀影响下拉索的动态疲劳可靠指标下降迅速，其降幅和降速均明显大于仅考虑腐蚀分级的情况.时变腐蚀条件下运营前期（前25年）拉索疲劳可靠指标降幅为腐蚀Ⅰ级到Ⅴ级的2.74倍、2.46倍、2.35倍、1.98倍和1.43倍；运营后期（25年至100年）的疲劳可靠指标降幅为腐蚀Ⅰ级到Ⅴ级的6.80倍、5.90倍、5.54倍、4.33倍和4.14倍.

5）腐蚀发生的时间对拉索疲劳可靠性具有显著影响.发生时间越早，拉索的疲劳可靠寿命越短.建议在既有桥梁斜拉索的运营维护和检测评估时，既要关注腐蚀等级对拉索疲劳可靠性影响，也应考虑腐蚀开始时间的不利影响.