美联航事件中的机票超售问题研究
,
(湖南工业大学 理学院,湖南 株洲 412007)
1 研究背景
2017年发生的美联航事件引起各方关注,事件起因是美国由来已久的机票超售制度。超售制度起源于20世纪初的欧洲国家,是航空公司为了避免出现空位损失,在飞机起飞前售出大于飞机实际座位数的一种销售模式。在实际运营过程中,总有订座之后因为各种原因不能来登机和起飞前退票的旅客,这种现象称为No-show[1]。文献[2]提出即使是完全售空的航班,在航班起飞前都会有5%~15%的旅客No-show,而为了减少No-show 旅客带来的空座损失,航空公司会采取超售的方式使得利益达到最大化。所以早期学者们主要根据No-show 人数分布来研究最优 超 售 水 平。1958年,M.J.Beckmann等[1]将Noshow 旅客带来的总损失用泊松分布和伽马分布进行拟合,发现伽马分布与航空实际情况比较符合,并依此提出一个静态超售模型,文献[3]运用Bellman-Jacobi 方程对模型进行分析,并求解了分段超售限制的最优解,该模型得到了各大航空公司的认可,并进行试用。但这一模型也有不利的一面,当登机人数超过了飞机实际座位数时,就会造成有些买了票的旅客无法登机,这种旅客被称为DB(denied boarding)旅客,而因此产生的一系列费用称为DB 补偿[4],文献[4]重点研究DB 旅客对超售收益的影响,并提出在保证盈利情况下航班能承受的最大DB 率。在美联航事件中就是因为被DB 旅客拒绝放弃登机,其他乘客也没人愿意放弃登机,才导致了事件的发生。相对发达国家来说我国的超售制度引入较晚,相关的制度也不够完善。但是随着人们生活水平的提高,航运已经成为人们经常选择的交通方式,特别是在节假日时,通常会出现一票难求的现象。所以,为了保证航班最大限度地使用运力,让更多旅客享受便捷的航空服务,机票超售不可避免。因为大众对机票超售的认同感很低,还有一部分甚至不知道机票超售概念,所以由“机票超售”引起的投诉和诉讼也不少。我国在这方面的研究还很少,其中文献[5-6]建立了基于二项分布的超售模型,但都只讨论No-show 人数对总收益的影响,未考虑DB 人数对总收益的影响;文献[7]同时考虑了这两个因素,借助Matlab 软件采用枚举法对问题进行求解,求出不同条件下的最佳销售量与其对应的超售总成本,并通过分析得出No-show 人数和DB 人数对最佳销售量和超售总成本的影响。
本文从航班总收益和最佳超售水平的角度出发,综合考虑了No-show 人数和DB 人数对最佳销售量和超售总成本的影响,最后得出了与文献[7]一致的部分结论,同时利用Matlab 软件绘制了函数图像,更直观地呈现了在不同条件下航班总收益与订票水平的关系,并从航班收益最高点附近的图像走势中得出No-show 人数和DB 人数对航班总收益的影响,然后在结论的基础上给出有效建议,并通过实例加以验证,增加了模型的可靠性。
2 基于二项分布的航空机票超售模型的建立
2.1 模型的假设与符号说明
为了强化旅客No-show 人数分布对于航空机票超售量的影响作用,便于模型的构建,作出如下3个假设:
假设1由于旅客到达机场是相互独立的,所以假设旅客达到是离散的。
假设2不考虑多级票价的情况,即航班的座位具有无差异性。
假设3No-show 人数k服从二项分布。
为了便于模型的构建以及问题的理解与说明,作以下符号设定:
f,为航班的飞行总成本,不随旅客人数的变化而变化,是一个固定值,作为常数处理;N,为航班飞机所载额定旅客数,即实有座位量;n,为飞行中飞机所载旅客数;g,为旅客所购机票的票价;m,为航班起飞前订座人数;k,为航班起飞时,Noshow 旅客人数;b,为航班起飞时,处理一名被DB的旅客给航空公司所在成的平均损失费用;s,为本次飞行完成后,航空公司所得的利润;p,为一个订座的旅客到达的概率;q,为一个订座的旅客“Noshow”的概率;p(k),为k人“No-show”的概率。
2.2 预期收益模型的建立
根据以上假设以及符号说明可知:在某次航班飞行周期中,需要登机的旅客人数为m-k,航空公司的预期收益为
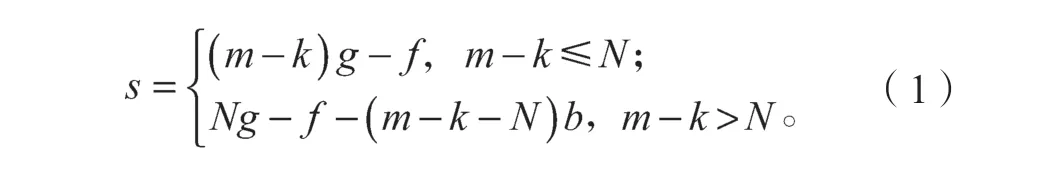
因为对于某一特定的航班来说,No-show 人数k是一个随机变量,所以航空公司的预期收益用预期收益的数学期望来表示,会更加适当和准确,它表示所有可能No-show 人数k值对应的情况下的预期收益乘以相对应的概率的和,记为,因此航班的预期收益为
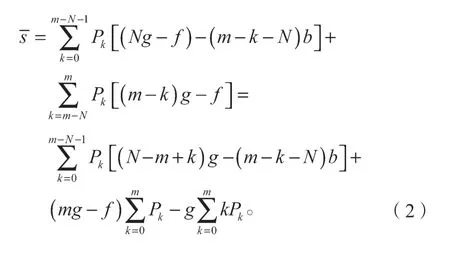
本模型的难点是如何确定Pk的值,需要考虑众多因素,对大量的数据进行分析,对航班的实时动态进行长时间的监控,才能确定Pk的值。为了便于问题的研究,假设旅客到达机场的概率是p,旅客被No-show的概率为q,又因为每个旅客到达机场是相互独立的事件,所以k服从二项分布,且

研究超售的任务是找一个最佳平衡点,使得航班的期望收益尽可能的大,而旅客被DB的人数尽可能的少,即最佳订票水平。所以在超售模型中,怎样正确评估航空公司对每个航班不同的DB,计算出航空公司所能承受的最大DB 旅客人数,是保证航班最大期望收益的关键。
设X为一次航班飞行周期中旅客被DB的人数,则可以算出至少z个旅客被DB的概率:
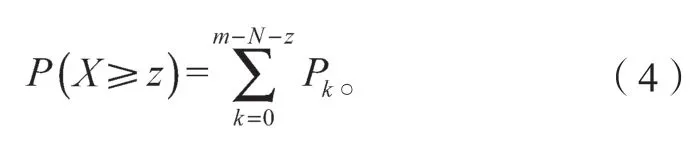
2.3 模型求解
在k服从二项分布的状态下,建立了航班的预期收益模型。因为且是k的期望值,用来表示,则可以简化模型(2),变为
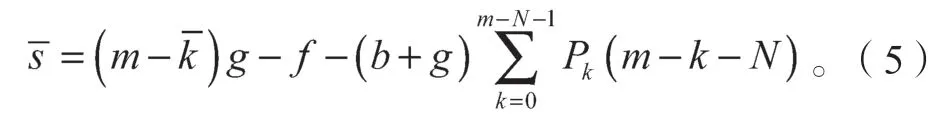
式中:f、g、b为不被航空公司短期因素影响的参数;N为不可变参数;k为外部不可控参数,不受航空公司控制;m为航空公司短期灵活可控参数。
则在某一特定情况下g、b、f、k、N是固定值,此时只随订票水平m的变化而变化。所以只要用Matlab 数学软件编制程序,输入任意g、b、f、k、N和订票水平m,就可以求出对应的。当取得最大值时,此时对应的m就是最优的超售水平。
又因为在一次飞行中,在载客率超过60%时,航空公司才能盈利,所以假设f=0.6Ng,且=qm,继续化简式(5)得:
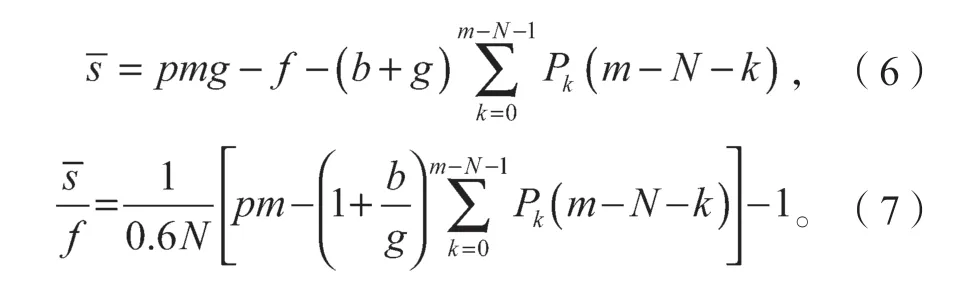
则此时最大期望收益变成了最大期望收益率的问题,且最大期望收益与处理一名DB 旅客的赔偿额和票价的比值b/g建立了函数关系。
3 模型分析
对式(7)用Matlab 软件编制计算机程序进行数值分析。以南方航空公司的波音B737-700为例,N=120,分以下两种情况讨论。
3.1 b 保持不变
取b/g=0.3,可得最大订票水平m的值随旅客的到达率p的变化曲线,如图1所示。
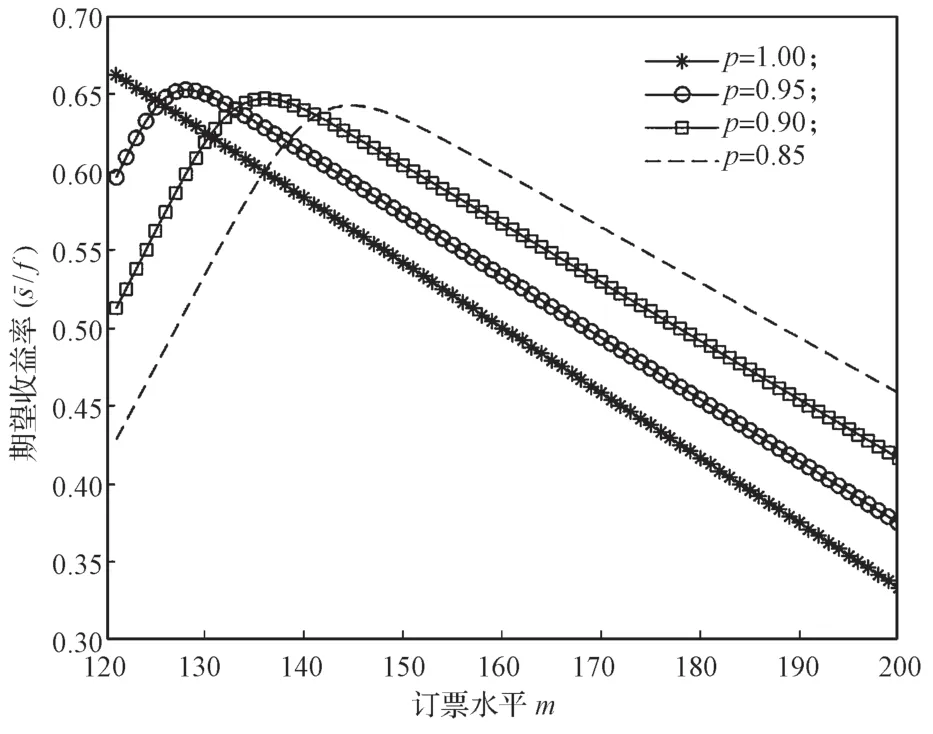
图1 不同p值下期望收益率/f 随订票水平m的变化情况Fig.1 Expected return /f changes with booking level m under different values of p
此时根据式(4)计算可得出,当获得最大期望收益时所对应的至少z个旅客被DB的概率,在本次模型中根据2017年本航班在每个飞行周期中被DB人数的众数来确定z的值,取z=3,则有:
当p=0.95,m=128时,P(X≥3)=0.378 4;
当p=0.90,m=136时,P(X≥3)=0.503 9;
当p=0.85,m=145时,P(X≥3)=0.579 5。
从图1中的曲线走势可以看出:
2)最佳订票水平m与旅客到达机场的概率p值成负相关,所以当旅客到达机场的概率p较低时,为了弥补因为No-show 带来的空位损失,就要提高超售水平,以保证航班的收益率;
3)最大期望收益率基本稳定,虽然随着旅客到达机场的概率p值的减小,最大期望收益率也在减小,但是收益率减少量与最优订票水平的上升量完全不成正比,这就说明了期望收益率受p值的影响较小,基本上是稳定的,也从侧面说明了采取超售的方式进行售票,可以在一定程度上保证航空公司的收益率,证明该方式是可行的;
4)至少有3 人被DB的概率与旅客到达机场的概率值成负相关,而旅客被DB的概率越大,航空公司进行DB 补偿的总金额就越大,航空公司的期望收益率就越小,所以,为了保证收益率,需要将P(X≥z)限制在某个范围内。
3.2 p 保持不变
取p=0.9,可得最大订票水平m随b/g变化的曲线,如图2所示。
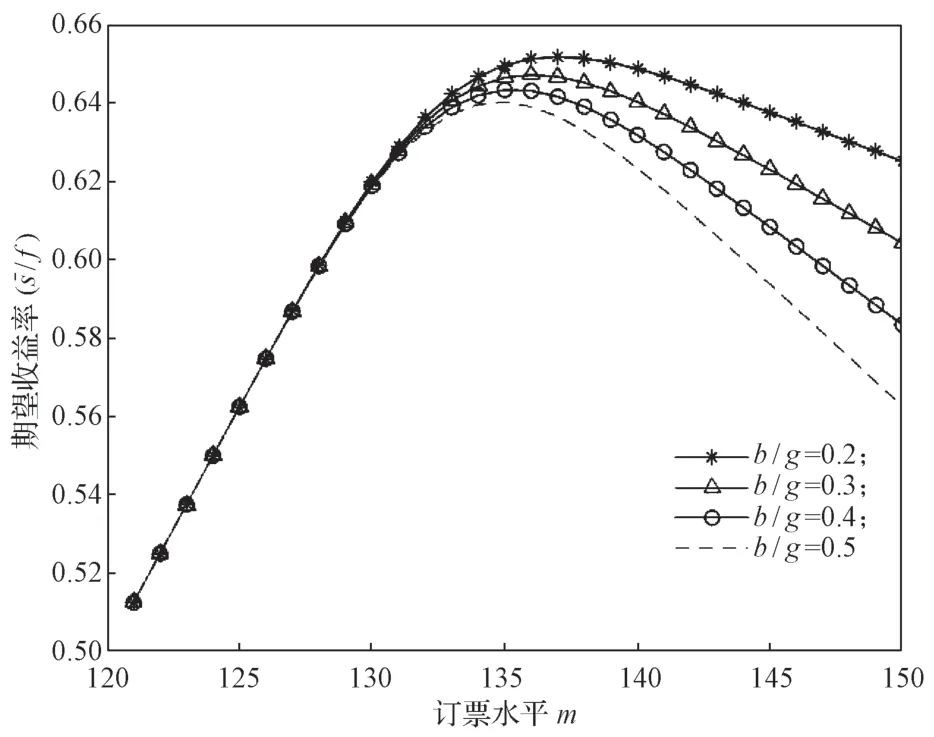
图2 不同b/g值下期望收益率/f 随订票水平m的变化情况Fig.2 Expected return /f changes with booking level m under different values of b/g
此时可根据式(4)计算得出,当获得最大期望收益时所对应的至少3个旅客被DB的概率分别如下:
当b/g=0.2,m=137时,P(X≥3)=0.604 0;
当b/g=0.3,m=136时,P(X≥3)=0.503 9;
当b/g=0.4,m=135时,P(X≥3)=0.400 9;
当b/g=0.5,m=135时,P(X≥3)=0.378 4。
从图2的曲线走势可以看出:
1)随着b/g值的增大,最大期望收益率减小,与之相对应的最大期望收益的订票水平m有所减少但是幅度比较小,这就说明最大期望收益率对于b/g的变化不敏感,结果与实际情况是相符合的,当处理一名DB的旅客的费用b很高时,航空公司一般会采取保守的超售政策,降低订票水平来规避DB的发生,减少因此而带来的损失;
2)至少3 人被DB的概率随着b/g值的增大而显著下降,直至不再发生变化变。这说明被DB的人数对b/g的变化非常敏感,所以确定合适的DB 补偿值b可以减少DB的概率,从而提高航空公司的预期收益率。
4 实例分析
选取广州-昆明航线,飞机型号为B737-300的航班进行实例分析,已知客容量N=120,机票价格g=1 000,DB 补偿额b=300。根据2017年1月—2017年12月中国民用航空局发表的旅客订票信息数据统计航班起飞时旅客登机状态分布,如表1所示(数据来源为http//www.caac.gov.cn)。
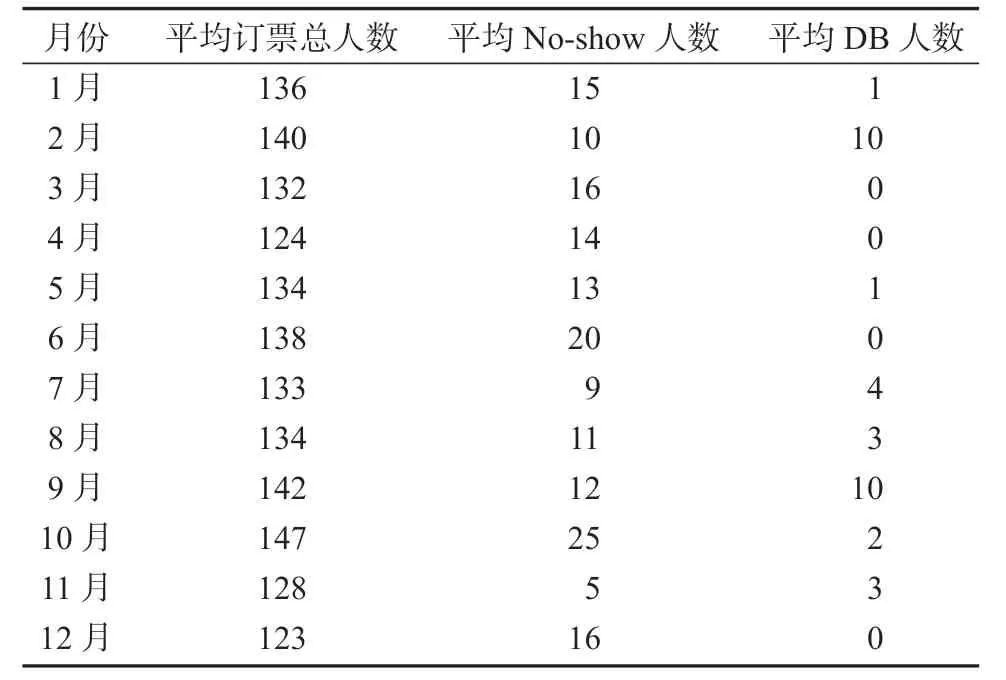
表1 航班起飞时旅客登机状态分布Table1 Passenger boarding status distribution at flight departure
根据航班起飞时旅客登机状态分布表中的数据,利用Matlab可得旅客在航班起飞前到达机场的概率p的均值为
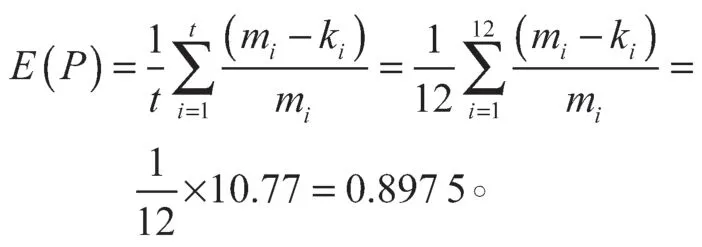
分别将N=120、g=1 000、b=300以及p=E(P)= 0.897 5 代入式(7)中,并利用Matlab 进行计算,得出航班在本次飞行中的最大期望收益率所对应的订票水平,如图3所示。
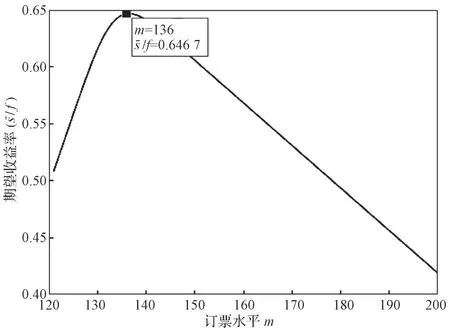
图3 实例结果图Fig.3 Case results chart
由图3可以看出,期望收益率随着订票水平的增加先增加后减少,在订票水平m=136时,期望收益率取得最大值。即航空公司在该航线上的最优订票水平为m=136。
虽然得出的结果136 略大于实际运营中的旅客的订票需求量134,但是这个结果仍然具有很大的现实意义以及较高的参考价值。第一,在不考虑多级票价的情况下,这个模型在一定程度上很大地降低了实际运营过程中存在的空座率和被DB 率,使更多的人能够成功出行的同时也提高了航空公司的收益;第二,根据实例中的条件,计算所得最大订票水平m所对应的收益率接近航班最大收益率;第三,这个结果为航空公司制定订票水平提供了量化依据。
综上所述,本模型与在实际运营过程中的拟合度较高,可以作为航空公司制定订票水平时的参考。
5 结语
本研究从No-show 旅客人数的分布入手,基于二项分布的航空机票超售模型,通过对模型的求解和分析,得到了航班的最优订票水平与旅客到达机场的概率以及处理DB 旅客的费用关系[8-10]。从仿真数值分析的结果可以看出,最大期望收益率的值基本稳定,这也说明了采用超售方式进行售票可以保证航空公司的稳定收益。从理论上来说模型具有一定的价值性。但是由于计算的复杂性,本研究暂时没有考虑多等级票价和旅客在订票周期中的订票状态对最优订票水平的影响,另外由于网上订票的普及性,人们订票越来越便捷的同时,退票也越来越迅速,所以如何对订票周期进行细分并建立动态多等级票价的最优订票水平是有待进一步研究的问题。

