Incompressible SPH simulation of solitary wave propagation on permeable beaches*
Chiaki Tsurudome,Dongfang Liang,Yuma Shimizu,Abbas Khayyer,Hitoshi Gotoh
1.Department of Engineering,University of Cambridge,Trumpington Street,Cambridge,UK
2.Graduate School of Engineering,Kyoto University, Kyoto, Japan
Abstract:Wave propagation on uniformly sloped beaches isa canonical coastal engineering topic that has been studied extensively in the past few decades.However,most of these studies treat beaches as solid boundaries even though they are often made of porous materials,such assediment and vegetation.Permeable beaches struck by tsunami-like waves have not been adequately investigated.It is expected that the degree of permeability playsa crucial role in mitigating the impact of the wave. This study examines solitary wave run-ups on sandy beaches using an incompressible smoothed particle hydrodynamics(ISPH)model.The permeability of the beach is considered to be directly related to the diameter of its constituent sand particles. To obtain a satisfactory pressure field, which cannot be achieved using the original ISPH algorithm, the source term of the pressure Poisson equation has been modified based on a higher-order source-term expression. Flowswithin the porousmedium are computed in the same framework asthoseoutside the porousmedium.In the current model,no transition zone is needed at the boundary of the porous structure.The wave-attenuation effect of the porous medium is discussed,with a particular focus on the relationship between the run-up height and grainsize.
Key words:Solitary wave,porosity,incompressible smoothed particle hydrodynamics(ISPH), run-up
Introduction
With populations and economic activities continuing to be concentrated in coastal areas,it is increasingly important to protect coastal infrastructure from wave impact and inundation during extreme events,which areexpected to occur more frequently.
Coastal hazards,such as hurricanes,typhoons,storm surges and tsunamis,are often accompanied by great run-up heights,leading to the inundation of the coastal areas.One of the most catastrophic recent events was the Sumatra Tsunami.An earthquake of Mw 9.3 struck Sumatra on 26 December 2004,which caused massive tsunamis[1]in the region.These tsunamishit Indonesia,Thailand, Malaysia, Myanmar,Bangladesh,India,Sri Lanka,Maldives and several African countries,and the total number of dead and missing was over 226 000.Another extraordinary event was Hurricane Katrina.In August 2005,extremely high waves and storm surge caused flooding and devastating loss of life throughout the southern part of Louisiana and Mississippi[2].Inundation was particularly severe in the coastal area of St Bernard Polder in New Orleans.
One of the possible natural solutions to mitigate these disasters is the coastal forest.The vegetation on the coast of Kuji,Japan,successfully attenuated the Tohoku Great Tsunami in 2011[3].When tsunami waves reach a coastline covered with a forest,they have to cross a soft barrier made of numerous trees.The flows passing through trees dissipate energy at a rapid rate.Hence, a narrow and tortuous flow path is the crucial mechanism for effective wave attenuation.A common engineering solution is to construct coastal dykes.Similar to the mechanism of the coastal forest,the main bodies of dykes are generally protected by porous materials,such as wave absorbing blocks placed in front of thedykes.
Wave run-up is a classic hydrodynamic problem.In the canonical configuration[4-10], a periodic or single wave propagates over a region of constant water depth and then climbs a plane beach of constant slope.In almost all past theoretical studies,the slope has been considered to be a solid boundary to the fluid flow.
In reality,however,most beaches are formed of sediment,which is a permeable material.Moreover,beachesare often covered with a vegetation layer.One way of modeling the influence of sediment grains and coastal vegetation is to add a friction term to the governing equations for the fluid motion.In rare situations,when the soil grains or concrete blocks are massive or the coastal forest is very sparse,these solid objects can be modelled directly using the discrete element method or traditional mesh-based method.
This paper aims to model permeable beaches as porous media in an incompressible smoothed particle hydrodynamics(ISPH)model.The numerical representation of porous media is not straightforward.The flow-governing equations must be modified, and the volume of smoothed particles should be allowed to change as they move into or out of the porous medium.We first give the numerical algorithm for our model,in particular the modifications to the existing ISPH framework.We then validate the newly established numerical model,before applying it to carry out a series of parametric studies to investigate the influence of the grainsize of the beach on the wave propagation and run-up height.The relationships between the run-up height and grainsize are summarised into a graph.
1.Two-phase ISPH model
1.1 Governing equations
In the ISPH method[11-16],the Navier-Stokes equations,including the continuity equation and the momentum equation,are solved.For flow in a porous medium,theextra flow resistanceforce isincluded.

where μis the dynamic viscosity coefficient,Kp is permeability,Nw is the porosity of the porous medium and Dc is the mean grain diameter of the porousmedium.
In a pure fluid region,the porosity value Nw is unity and thus the resistance force becomes zero,so the last term on the right-hand side of the momentum equation (2)vanishes.Then,Eq.(2)is reduced to the standard Navier-Stokesequations.
1.2 Overall computational algorithm
Figure 1 illustrates the overall computational procedure.

Fig.1 (Color online)Overall computational algorithm
1.3 Numerical treatments of the porous medium
The standard SPH discretisation is not repeated here.Only a few special numerical treatments concerning the flow in the porous medium are briefly introduced below.
Dummy particles are placed in the region occupied by the porous medium.These dummy particles are not involved in the solution of partial differential equations but are used only for the convenience of updating the permeability and density at each time step.The porosity of a smooth particle varies between unity in the pure-fluid region and a value smaller than 1 in the porous region.With the help of dummy particles,porosity gradually changes over a distance of two times the smoothing length at the interface between the pure-fluid region and the porous medium region,but no transition zone needsto be explicitly specified.
The density of a fluid particle inside the porous region should be lower than that of a particle outside the region,considering the existence of the solid skeleton that forms the porous structure.As the fluid particle’s mass does not change when it moves into and out of the porous region,the apparent volume of the fluid particle will change according to the apparent density.Theapparentdensity conceptusedhereis similarto thatused byRen etal.[14]andAkbari[17],in which the density and volume of a smooth particle j vary with the porosity as follows:

where ρwrepresents the density of a particle in the pure-fluid region,and m is the mass of a smooth particle.According to the smooth particle interpolation algorithm,a variable at position i can be approximated as

where φcan be any variable,such as pressure or velocity,and Wijis the value of the kernel function between particles i and j. It can be seen that the weight of the interpolation is increased in the porous medium region,as the fluid particles there have a smaller density and a larger volume.Hence,the more sparsely distributed water particles in the porous medium region,as compared to the smoothing particle distribution in the pure-fluid region,still satisfy the consistency condition of the smoothing interpolation.
1.4 Modified pressure poisson equation
In ISPH,the time increment from t to t +1is divided into two steps,i.e.,the prediction step t*and the correction step t**,to enforce the condition of incompressibility.The discrete form of the mass conservation equation is

Combining them yields

This is the pressure Poisson equation (PPE),and the right-hand side is referred to as the standard source term in this paper.Although the standard source term has been widely used in ISPH simulations,many have pointed out that the calculated density of the particle i cannot maintain exactly the same value asρ0due to the numerical errors in the SPH discretisation.This canresultina severefluctuationofthepressure field.Khayyer etal.[11,18]proposed anewapproach,called the higher-order source (HS)scheme,to eliminate numerical errors and obtain a more accurate pressure field.
Based on the SPH formulation,the density of the target particle i can be calculated by

The time derivative can be written as

Thus,the PPE can be modified as

Although the smooth pressure field can be obtained through the HS scheme,the fluid volume cannot be exactly conserved,and thus the calculation becomes unstable if the computational time becomes long.To overcome the weakness of this approach,the hybrid source term was developed[12-13,19].The modified PPE can be written as

whereθisa combination ratio.
1.5 Generation of solitary waves
A numerical wave paddle is used to generate solitary waves in some of the case studies to be discussed below. Goring’s[20]theory is used to specify the paddle’smotion to generate solitary waves.

where ξis the horizontal position of the wave paddle,βis the outskirts decay coefficient and c isthe wave speed.

2.Model verific a tio ns
2.1 Dam-break flood waveimpact on a porousblock
To validate this ISPH model,the numerical results for a dam-break flow passing through a porous blockhavebeencompared with the experimental data obtained byLiuet al.[21].
As sketched in Fig.2,the water tank used in the experiment was 0.892 m long,0.440 m wide,and 0.580 m high.A 0.037 m high,0.290 m long porous block was placed in the section from x =0.300 m to x =0.590 m.A gate was built 0.020n m away from the front (left)side of the porousdam to create a water reservoir with a water depth of 0.250 m. The porous block was confined to the initial region to ensure that the porousmedium did not move.

Fig.2 (Color online)Sideview of theinitial water level and the position of the porous dam
This is a vertical two-dimensional problem.The dimensions of the simulation are illustrated in Fig.2.The porous dam is made of crushed rocks.The equivalent mean grain diameter is 0.0159 m and the initial porosity is 0.49.Figure 3 compares the numerical results and experimental data for free-surface profiles during the period when the flow passed through the porous dam.It can be seen from the comparison that the predicted wave shapes by the two-phase ISPH model,indicated by the distribution of smoothing particles that are coloured according to pressure,agree well with the experimental data,indicated by the black circles.

Fig.3 (Color online) Comparison of free-surface profiles during flood wave interaction with a porous block
2.2 Solitary wave run-up on a solid beach
There have been numerous experimental and analytical studies of the problem of the solitary wave run-up on uniform solid slopes.In the problem setup,a uniform slope of angle βrepresents an idealised beach connecting the flat offshore region and the land.The symbol h is the undisturbed water depth in the flat region,ηis the water surface position above the still water level,and H is the amplitude of the incident wave.The run-up height,R,is defined as the maximum vertical elevation above the still-water level reached by water on the slope.During shoaling from deep to shallow waters,the asymmetry of the wave profiles increases,and the wave height grows.Wave breaking may occur,if the incident waves are high and the slope isgentle.
For non-breaking solitary waves and N-waves,
analytical solutions havebeen developed todescribe theirrun-upprocess.Synolakis[4-5]derivedthe first run-up formula for incoming solitary waves.Numerous empirical formulae have been proposed for the prediction of breaking wave run-up heights.
To validate our computational method, the numerical model has been applied to Synolakis’s[4-5]laboratory datasets for solitary waves with different degrees of non-linearity, propagating up an idealised plane beach. The beach has a uniform slope of 1 in 19.85. Apart from measuring the maximum runup height, Synolakis’s[4-5] experiments also quantitatively visualised the wave profiles using still photographs of the water surface. In one verification example, the water depth is 0.21 m, and the wave amplitude-todepth ratio is 0.28. The computational domain is 10 m long in total, consisting of a 2-m long flatbed channel and an 8-m long sloping beach. The initial particle spacing and time step are 0.005 m and 0.00025 s,respectively.
A sequence of the measured and predicted water surface profilesasthe solitary wave ran up the slope is shown in Fig.4.The thick black line represents the solid beach.The thin black lines represent the numerical predictions,while the blue symbols represent the laboratory measurements.In Fig.4,the horizontal length and the elevation have been normalised with the undisturbed water depth,while the three times,corresponding to the three snapshots,have been normalised by the undisturbed water depth and gravitational acceleration.Figure 4 shows that the present simulation accurately captures the wave transformation over the slope,as well as the advancing and retreating of the shoreline.As the solitary wave climbed up the slope,its length shortened;its front steepened,and its amplitude grew.In this example,the solitary wave breaks when the non-dimensional time is30.1.
Synolakis[4]proposed the relationship between the run-up height and wave height of a non-breaking solitary wave asfollows

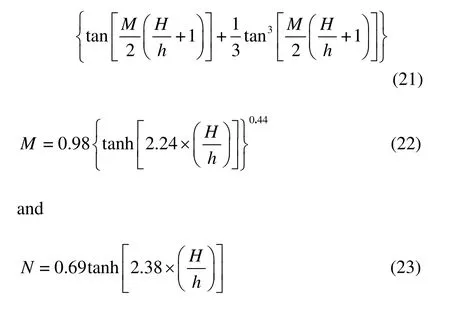

Fig.4 (Color online)Evolution of the surface profile as the solitary wave propagates on a solid beach
Several combinations of the undisturbed water depth and wave height were considered. Figure 5 shows that our predictions of the run-up height on a solid beach agree well with the analytical results.Figure 5 assembles a number of analytical, empirical and numerical results available for the run-up height on the slope. The current predictions are in close agreement with the nonlinear theories by Synolakis[4],for both non-breaking and breaking waves.
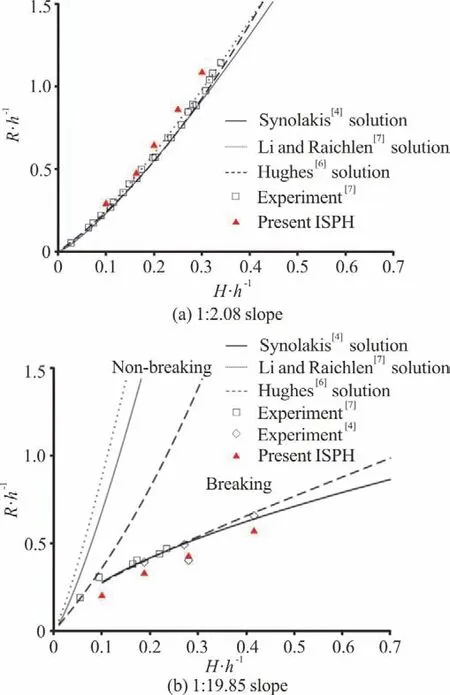
Fig.5 (Color online)Run-up height versuswave height
3.Solitary wave run-up on porous beaches
The present model is then applied to the simulation of solitary wave propagation over permeable beaches to investigate the relationship between the run-up height and the grainsize of the porous medium.A schematic diagram of the computational domain is shown in Fig.6.The 1:2.08 sloped porous beach is placed at x =2.07 m .Its porosity is fixed at 0.49,but the mean grainsize is varied from 0.0002 m to 0.2000 m.Solitary waves with H / h=0.163 and H / h=0.25 are generated at the inlet.The highest point at the water-porous boundary is defined as the run-up height.
Figures 7 and 8 show examples of wave propagation over porous beaches with grainsize 0.25 mm and 1.00 mm,respectively.The generated wave is H / h=0.163.Thanks to the hybrid source term of the PPE,the predicted pressure field is free of numerical oscillations.The wave cannot propagate through the porous beach during run-up when the grainsize is 0.25 mm,whereas apparent penetration is observed with a grainsize of 1.00 mm.

Fig.6 (Color online)Initial setup of porous beach run-up

Fig.7 (Color online)Wave profile evolution on a porous beach,Dc=0.25 mm
All results are summarised in Fig.9.When a porous medium consists of very fine materials,the movement of fluid in the medium is limited.The run-up height isseen to converge to around 0.36 in the case of H / h=0.163 at very small grainsizes.Since the normalised run-up height on a solid slope is 0.445,the wave mitigation effect due to the porous medium can be estimated to be around 19%when the grainsize is 0.0002 m.Similarly,in the case of H / h=0.25 the mitigation effect is only around 5%when the grainsize is very small.If the grainsize is large,however,fluid particles can effectively propagate into the beach, so the run-up height is lowered.For example,when the grainsize is 0.2000 m and the wave height H/h= 0.163,the normalised run-up height isonly 0.269.

Fig.8 (Color online) Wave profileevolution on a porous beach,Dc=1.00 mm

Fig.9 (Color online)Dependence of the runup height on grainsize
4.Conclusions
An ISPH model for simulating fluid interaction with a porous medium is presented,which does not require an explicit transition zone at the interface.The present model showed good agreement with experimental results of the porous dam-breaking,and with analytical solutions and experimental measurements of solitary wave run-up heights on uniformly sloped beaches.Satisfactory pressure fields were also obtained thanksto a modified PPE source term.
The present model was used to simulate the solitary wave propagation and run-up on permeable beaches,and the effect of the sediment particle size was examined in detail.The results indicate that the run-up height converges to constant values for cases with either extremely small grainsizes(smaller than 0.0002 m)or extremely large grainsizes(larger than 0.1000 m).Between these values,the run-up height decreases with the grainsize.Further simulations and analyses need to be conducted with a wider set of parameters,involving more wave heights,slope angles and other physical properties of porous beaches.
AcknowledgementsThis work was supported by the Royal Academy of Engineering UK-China Urban Flooding Research Impact Programme (Grant No.UUFRIP100051),the Ministry of Education and State Administration of Foreign Experts Affairs 111 Project (Grant No.B17015)and the Cambridge Tier-2 system operated by the University of Cambridge Research Computing Service (http://www.hpc.cam.ac.uk)funded by EPSRCTier-2 capital (Grant No.EP/P020259/1).
- 水动力学研究与进展 B辑的其它文章
- Development and application of a new random walk model to simulate the transport of degradablepollutants*
- Some notes on numerical simulation of the turbulent cavitating flow with a dynamic cubic nonlinear sub-grid scalemodel in OpenFOAM*
- Predictions of bulk velocity for open channel flow through submerged vegetation*
- On solitary wave in nonuniform shear currents *
- Fission law of solitary waves propagating over sharply variable topography *
- A TensorFlow-based new high-performance computational framework for CFD *

