GRAPES全球/区域集合预报系统10年 发展回顾及展望
陈静 李晓莉
(中国气象局数值预报中心,北京 100081)
0 GRAPES全球和区域集合预报发展历程
数值预报是当代天气预报的基础,但由于为数值模式提供初值的观测资料和同化方法具有误差,造成模式初值不可避免地存在误差,而非线性大气运动的复杂性和混沌特性,导致预报结果对初值误差非常敏感,由此初值获得的数值模式解仅是真实大气的一个可能解,单一数值预报结果存在不确定性[1]。而集合预报技术则是通过一定的数学处理方法生成多个略有差异的初值或者略有差异的模式,获得多个数值模式解,进而通过计算大气运动状态概率密度函数来定量估计单一确定性数值预报的不确定性。近20年来,利用集合预报描述单一确定性数值预报的不确定性,在各大业务数值预报中心获得广泛应用,与资料同化、动力框架、物理过程一起构成了当代数值预报技术的四个发展方向,成为数值预报业务核心系统[1]。
当前集合预报系统主要有三种:全球中期集合预报、区域中尺度短期集合预报和对流尺度集合预报,它们重点解决不同时空尺度的预报问题。全球中期天气集合预报(Global Medium-range Ensemble Prediction system,GEPS,预报时间为3~15 d)通常设计用于3~15 d的中期天气预报,水平分辨率通常在10~50 km ,是各大数值预报中心主要业务组成部分。区域集合预报系统(Regional Ensemble Prediction System,REPS)主要采用较小范围的区域模式,具有较全球模式更高的分辨率,通常在5~30 km,主要着眼于1~3 d的短期天气预报,因此可以用于预报天气系统中的一些局部细节,还能够更好判断一些强天气系统可预报性;通常区域集合预报系统需要从全球集合预报系统中获得侧边界条件(天气系统从有限区域范围以外移入有限区域内的边界)。对流尺度集合预报系统(Convective-Scale Ensemble,CSE )主要采用1~3 km对流尺度模式,主要目的提供对流运动细节的预报不确定性,预报时间通常是0~36 h,1~3 km对流尺度的区域集合预报在欧美发达国家已经成为核心业务,为提高强对流天气预报预警能力提供基础。
中国气象局国家气象中心早在20世纪90年代开始发展全球集合预报系统[2],1996年建立了基于时间滞后方法的T63L16全球集合预报,集合预报成员12个,预报时效10~13 d,1999年升级为基于奇异向量方法的T106L19全球集合预报[3],集合预报成员32个,预报时效10 d。2007年建立了基于增长模繁殖法的T213高分辨率数值集合预报系统[4],集合预报成员15个,预报时效10 d,2014年,将T213集合预报升级为T639集合预报系统,在集合预报成员中增加了随机物理过程倾向项扰动方案[5]。中国气象局区域集合预报的发展始于2006年,在世界气象组织(World Meteorological Organization,WMO)北京奥运会研究示范项目[6]支持下,国家气象中心基于美国WRF模式,采用增长模繁殖法建立中国区域集合预报系统[7],2010年11月15日实现业务化运行,模式不确定性采用多物理过程组合,系统水平分辨率15 km,侧边界来自T213全球中期集合预报系统,15个集合预报样本,每天运行4次。
GRAPES模式是中国气象局自主研发的新一代数值天气预报模式[8]。GRAPES集合预报技术发展始于区域集合预报研究,2005年,同样在WMO北京奥运会研究示范项目持下,中国气象科学研究院采用增长模繁殖法建立多初值多物理GRAPES区域集合预报系统[9],随后应用集合变换卡尔曼滤波初值扰动方法开展GRAPES区域集合预报试验[10]。2007年以来,通过中国气象局公益性行业专项“面向TIGGE的集合预报关键应用技术研究”(GYHY200706001)、“基于多模式集合预报的交互式应用技术研究”(GYHY200906007)、“GRAPES区域集合预报多尺度混合扰动关键技术研究”(GYHY201506005)以及中国气象局GRAPES专项经费支持,发展集合变换卡尔曼滤波(Ensemble Transform Kalman Filter,ETKF)初值扰动技术[11-19],研发与中国气象局全球集合预报系统数据耦合的GRAPES区域集合预报统,2014年基于集合变换卡尔曼滤波初值扰动技术的中国区域集合预报系统(GRAPES Regional Ensemble Prediction System,GRAPES-REPS)v1.0版本替代WRF区域集合预报系统,成为国家气象中心业务化区域集合预报系统,该系统水平分辨率15 km,集合预报成员15个;2015年该系统初值扰动技术更新为多尺度混合初值扰动方法[20],中尺度初值扰动信息来自GRAPES区域集合预报系统的集合变换卡尔曼滤波方法,大尺度初值扰动信息来自T639全球集合预报系统的增长模繁殖方法,GRAPES-REPS区域集合预报系统升级为v2.0版本,2019年9月,随着基于奇异向量初值扰动方法的GRAPES全球中期集合预报业务化运行,GRAPES区域集合预报的侧边界扰动来源由T639全球集合预报更新为GRAPES全球集合预报系统,同时初值扰动技术和模式扰动技术均实现业务更新,业务系统升级为v3.0版本[21]。
GRAPES全球集合预报的研究始于2008年,最初采用全球集合变换卡尔曼滤波方法建立GRAPES全球集合预报[22],随着GRAPES全球四维变分同化技术的发展,在中国气象局公益行业专项“GRAPES全球模式集合预报奇异向量初值扰动方法研究”(GYHY201006015)以及中国气象局GRAPES专项经费支持下,国家气象中心开始组织发展基于奇异向量初值扰动技术的GRAPES全球集合预报系统[23-27],经过近10年的研究开发,基于奇异向量初值扰动方法的GRAPES全球中期集合预报于2018年12月实现业务运行,替代了T639全球集合预报系统,国家气象中心由此建立了一套完整的GRAPES数值预报业务体系[28]。
在代表GRAPES模式的不确定性方面,研究人员在国家气象中心T213和T639全球中期集合预报模式不确定性扰动研究基础上,利用GRAPES区域集合预报和全球集合预报开展了多种模式扰动方法研究,如多物理过程组合方法(Multi-Physics,MP)[21],随机物理过程倾向扰动方法(Stochastically Perturbed Parameterization Tendencies,SPPT)[29],随机动能后向散射方法(Stochastic Kinetic Energy Backscatter,SKEB)[30];随机参数扰动方法(Stochastically Perturbed Parameters,SPP)[31]。SPPT方案分别于2015年和2018年在GRAPES-REPS区域集合预报v2.0版本和GRAPES-GEPS v1.0版本中实现业务应用[21,28],SEKB方案于2018年在GRAPES-GEPS全球集合预报v1.0版本中实现业务应用[28]。
2019年,GRAPES全球集合预报系统v1.0和GRAPES区域集合预报系统v3.0实现一体化运行。与单一确定性预报业务系统相比,集合预报业务系统组成更复杂,系统更庞大,不仅需要研究代表GRAPES模式初值和模式不确定性的初值扰动方法和模式扰动方法,还需要进行集合预报系统后处理和产品开发。受篇幅限制,本文将侧重介绍在GRAPES-GEPS v1.0业务版本和GRAPES-REPSv3.0业务版本中应用的初值扰动技术、模式扰动技术、业务系统参数和预报效果,并分析存在的问题,展望未来发展。
1 GRAPES全球模式奇异向量初值扰动技术
集合预报的核心问题是如何产生代表分析误差概率分布的初值样本集合。奇异向量法(Singular Vectors,SVs)是国际上常用的集合预报初值扰动方法,其基本原理是利用非线性动力学理论中的有限时间不稳定理论,计算切线性模式的奇异值和奇异向量,利用最大奇异值对应的奇异向量就是增长最快的扰动原理,获得一系列的初值扰动。奇异向量初值扰动方法首先成功应用于欧洲中期天气预报中心(ECMWF)集合预报系统[32],随后在主流数值预报中心全球集合预报业务中获得了较广泛应用。GRAPES全球四维变分系统发展的切线性和伴随模式为GRAPES全球集合预报SVs扰动技术的研究和发展提供了条件。通过构建适合GRAEPS模式特点的SVs求解计算所需的总能量模,开发SVs并行计算,最终建立了基于奇异向量初值扰动技术的GRAPES全球集合预报系统[28]。
1.1 奇异向量数学计算方案
GRAPES全球集合预报奇异向量初值扰动技术包括计算奇异向量和构建初值扰动结构的数学处理方案两大部分。计算奇异向量的数学处理方案由全球热带外地区和热带气旋奇异向量计算两部分组成,具体的数学处理方案简述如下。
1.1.1 热带外奇异向量计算方案
GRAPES全球奇异向量求解可归结为演化扰动向量Xt模与初始扰动向量X0模之间比值的最大化问题[25],如公式(1):

其中:L是GRAPES四维变分同化系统中的切线性模式(Tangent Linear Model,TLM),LT是伴随模式(Adjonint model,ADM),E是衡量扰动大小权重模,x表示奇异向量,λ为对应的奇异值。P是投影算子,其作用是将目标区之外奇异向量扰动设置为零。由式(1)可见,影响奇异向量结构的因素有三点:1)奇异向量扰动大小权重模E的定义;2)切线性模式 L及伴随模式LT的特点,主要为线性化物理过程参数化方案的使用;3)切线性模式L向前及伴随模式LT向后的积分时间长度(最优化时间间隔)。
GRAPES全球奇异向量采用总能量定义权重模[26],设GRAPES全球TLM和ADM的预报量-水平风分量(u, v),扰动位温(),扰动无量纲气压()对应的扰动量(可表示为:,总能量模E的计算如下:
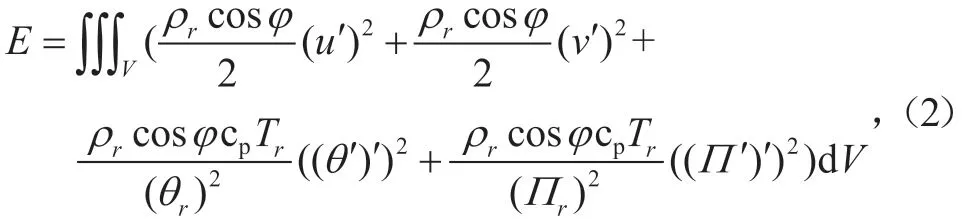
式中:前面两项之和为扰动动能(kinetic energy,KE)模,后两项之和表示扰动位能(potential energy,PE)模,其中第三项和第四项分别表示位能中扰动位温和扰动无量纲气压分量的贡献,为地形追随坐标,λ和φ分别代表模式球面坐标系中的经度和纬度,cp为干空气的定压比热。Tr,θr,Пr及ρr分别表示参考温度、参考位温、参考无量纲气压及参考密度,其计算公式分别,,式中,Rd为干空气气体常数,ρr为标准大气,Tr为参考温度,g为重力加速度。
表1是GRAPES全球奇异向量计算参数配置,GRAPES全球切线性模式L及伴随模式LT水平分辨率为2.5°×2.5°,垂直60层,且在切线性模式及伴随模式采用了线性化边界层方案(Planetary Boundary Layer,PBL)和线性化阻塞流拖曳方案(Mountain Blocking,MB)。GRAPES全球奇异向量的求解采用Lanczos迭代算法,在迭代过程中需多次积分切线性模式L及伴随模式LT。热带外奇异向量计算目标区分别为北半球中高纬度(30°—80°N)区域、南半球中高纬度(80°—30°S)区域,计算精度为0.001,通常迭代50次可以获得30个奇异向量;此外,还利用48 h前的初始奇异向量经过48 h的线性演化,得到与初始奇异向量同时次的演化奇异向量。

表1 GRAPES全球奇异向量计算参数配置 Tabel 1 Configuration of SVs scheme in GRAPES-GEPS
1.1.2 热带气旋奇异向量计算方案
副热带SVs和演化SVs在热带地区几乎为零,不能反映热带气旋(Tropic Cyclone,TC)的初始不确定性,造成TC集合预报技巧较低。考虑热带气旋系统的特殊性,在GRAPES全球集合预报中发展了热带气旋奇异向量计算方案[33],即如果有热带气旋生成,则以热带气旋为中心10个经纬度区域为目标区计算奇异向量,最多可以计算6个热带气旋奇异向量。
从表1 可见,加上热带外的南北半球区域,GRAPES奇异向量计算目标区域有三个,不仅生成了能体现南北半球中高纬度大气的斜压不稳定扰动发展的奇异向量,还在有热带气旋时生成考虑热带气旋发展的奇异向量。
1.1.3 奇异向量结构特征
图1是2013年5月8日00UTC北半球第1奇异向量扰动分布中比较显著的局地奇异向量扰动[25],可见初始时刻位温扰动表现出随高度向西倾斜的特征,体现了大气对流层中下层常存在的、有利于天气系统发展的斜压结构。在最后演化时刻的位温扰动分布尺度变大,垂直结构演变成了随高度无明显倾斜的正压结构特征,扰动量值分布上也呈现出上传和下传的特征。此外,初始时刻和最后演化时刻奇异向量扰动能量模
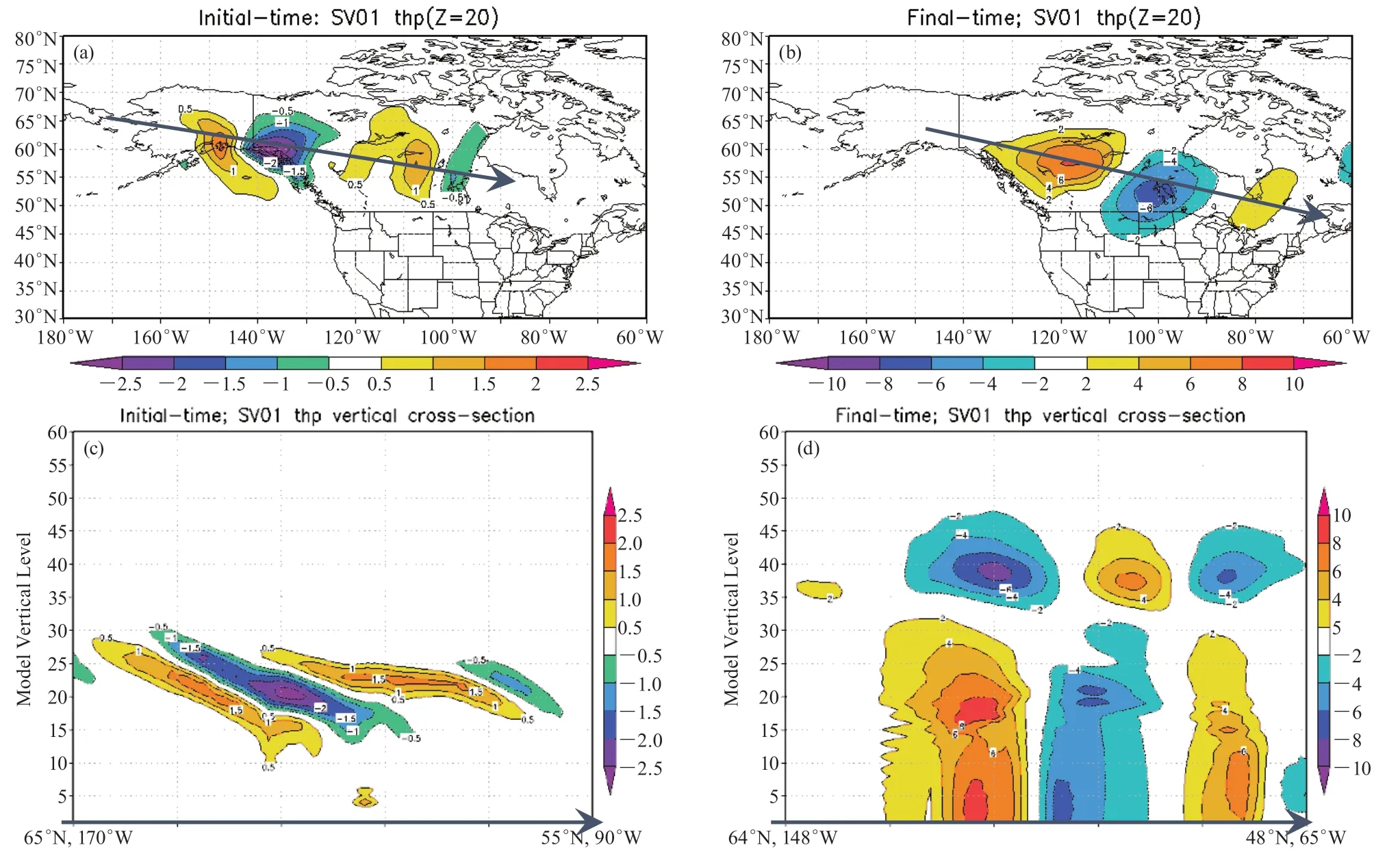
图1 北半球第1SV位温扰动(放大1000倍,单位:℃)在模式第20层的水平结构(a,b)及沿着箭头所示的径向垂直剖面(c,d)(a,c)初始时刻;(b,d)最后演化时刻[24] Fig. 1 Horizontal structure at model level 20 (a, b) and vertical cross-section (along arrows shown (c, d) of potential temperature perturbation(multiplying by 1000, unit: ℃)of 1st SV over NH at initial time (a, c) and final evolved time (b, d) [24]
垂直结构显示(图略),GRAPES奇异向量扰动能量的线性演变较好地体现了大气对流层中斜压不稳定及其能量垂直传播特征和升尺度的能量转移特征,体现天气尺度的大气斜压不稳定能量及演变。
1.2 基于奇异向量的集合预报初值扰动构建
基于上述计算产生的北半球初始奇异向量和演化奇异向量、南半球初始奇异向量和演化奇异向量、热带气旋初始奇异向量,采用高斯取样技术构造GRAPES全球集合预报初值扰动场[26,33]。
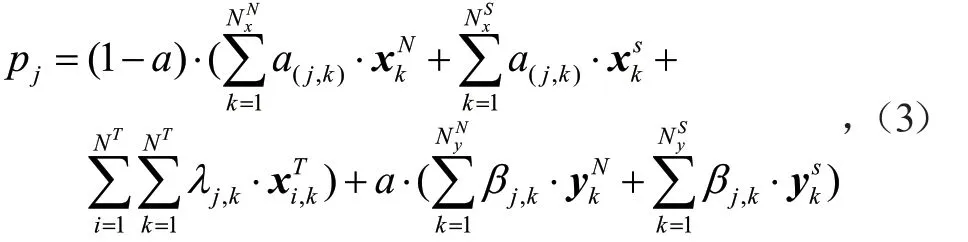
其中,pj是第j个初值扰动,a是演化奇异向量的权重,是第k个北半球初始奇异向量,是第k个北半球演化奇异向量,代表北半球初始奇异向量的个数,代表北半球演化奇异向量的个数,是第k个南半球初始奇异向量,是第k个南半球演化奇异向量,代表南半球初始奇异向量的个数,代表南半球演化奇异向量的个数。,其中γ是可调经验系数,可以控制初值扰动振幅,是SV或演化SV的尺度化放大因子,可通过式(4)计算得到:
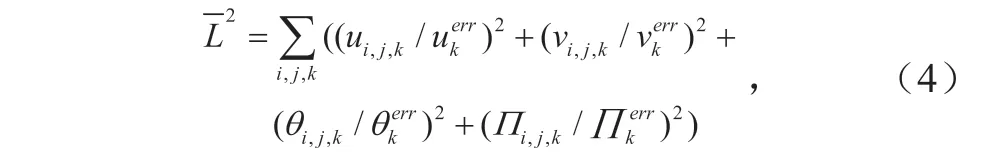
式中:i,j,k分别对应模式网格经度、纬度和垂直层数变量,ui,j,k是SV或演化SV的纬向风扰动分量,vi,j,k是SV或演化SV的经向风扰动分量,θi,j,k是SV或演化SV的扰动位温扰动分量,Пi,j,k是SV或演化SV的扰动Exner气压扰动分量,是纬向风标准差,是经向风标准差,是扰动位温标准差,是扰动Exner 气压标准差。通过大量参数敏感性试验,GRAPESGEPS v1.0初值扰动计算方案,通过敏感性试验确定可调参数α=0.1,γ=0.06。
2 GRAPES区域集合预报初值扰动技术
区域集合预报中普遍采用两种初值扰动构造方法,一种是采用全球集合预报初值扰动动力降尺度产生,另一种是采用在全集合预报中应用较成熟的初值扰动方法(如BGM,SVs,ETKF等初值扰动方法)产生。对于降尺度方法而言,由于全球集合的分辨率有限,动力降尺度产生的扰动信息缺乏小尺度不确定性信息,而这些小尺度不确定性信息对于局地性强天气过程很重要。GRAPES区域集合预报业务系统采用了集合变换卡尔曼滤波(ETKF)方法单独构造扰动初值。
2.1 集合变换卡尔曼滤波(ETKF)初值扰动方法
2.1.1 ETKF 初值扰动数学处理方案
集合变换卡尔曼滤波(ETKF)初值扰动方法是基于卡尔曼滤波理论发展而来,由集合预报扰动方差和观测误差方差快速估计分析误差的一种初值扰动技术[34]。在GRAPES区域集合预报系统中,将预报扰动向量更新为分析扰动,利用变换矩阵T来建立预报扰动和分析扰动的关系,如公式(5),即通过变换矩阵T对当前时刻预报扰动向量进行线性组合,构造当前时刻的分析扰动[12-13]

ETKF初值扰动方法的核心是如何获得变换矩阵T,在GRAPES区域集合预报ETKF方案中,采用Wang等[34]方法,假设预报扰动Xf的协方差能够代表预报误差协方差Pf,定义,则T的表达式为:


其中,di为第i时刻被R-1/2标准化的更新向量(innovation),N为观测数目,λi为式(6)中Γ的对角元素,αi将对集合扰动方差进行调整,使预报扰动方差与控制预报误差方差在全球观测空间中保持一致。
同时,为了使集合扰动成员相对于集合平均中心化,采用球面单形中心化方案[34],即得ETKF的初值扰动的最终表达式:

2.1.2 ETKF 初值扰动结构特征
ETKF方法的一个重要特征是能够吸收观测信息,对扰动进行调整。GRAPES区域集合预报采用模拟观测资料[18]的方法,将全球背景分析场插值到观测空间作为模拟观测资料。图2是观测空间水平分布以及连续40 d垂直平均的U分量风扰动绝对值的分布。可以看出高原地区以及西太平洋海洋地区的观测较为稀疏,因此这些地区初始分析场的不确定性较大,青藏高原地区以及西太平洋海洋地区扰动量级较大,最大值可达4 m/s,而在观测分布较密集的中国大陆东部地区,扰动量级较小。
在GRAPES区域集合预报业务系统v3.0版本中,因侧边界扰动来自GRAPES全球非静力模式,为保障业务系统积分稳定性,ETKF投影矩阵的计算变量为动量场变量(u,v),放大因子计算变量为动量场变量(u,v)和比湿变量q,ETKF初值扰动计算采用6 h循环扰动计算方案,每天运行4次,分别为00Z、06Z、12Z、18Z,其中00Z与12Z均作84 h预报,06Z与18Z只做6 h预报,为ETKF循环提供6 h预报扰动场。
2.2 基于ETKE 的多尺度混合初值扰动方法
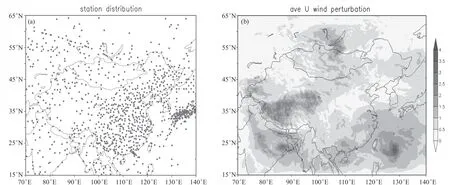
图2 观测站点及初始扰动水平分布[14] (a)观测站点分布图(黑点为测站位置);(b)40 d垂直平均的U分量风初值扰动(单位:m/s) Fig. 2 Horizontal distribution of observation stations and initial perturbation (unit: m/s) [14] distribution of observation stations (10cations of observation stations shown as black dots); (b) 40 d vertically averaged horizontal distribution of U wind perturbation
业务实践表明,全球集合预报动力降尺度的区域集合预报扰动结构可以产生更多的大尺度不确定性信息。在GRAPES区域集合预报v2.0版本中,应用了多尺度混合初值扰动技术(Multi-Scale Blending,MSB)[20]。该方法的原理是基于区域和全球集合预报初值扰动结构共同构建多尺度混合初值扰动场,其中“小尺度”扰动来源于区域集合预报ETKF生成的初值扰动,“大尺度”扰动来源于国家气象中心T639全球集合降尺度扰动。通过一个数字滤波器2D-DCT[35]对全球集合预报和区域集合预报的扰动结构进行滤波,需要注意的是,对不同层次或者不同变量,滤波器的临界波长不同(如表2所示),还采用2D-DCT反变换重构来自全球集合预报的大尺度扰动和来自区域集合预报的小尺度扰动结构。该方法于2015年应用于GRAPES区域集合预报业务化系统v2.0版本中。
2.3 区域集合预报台风涡旋条件性重定位方案
通过对GRAPES-REPS台风路径集合预报的诊断分析发现,虽然部分集合成员的台风涡旋中心初始定位经过扰动后比较合理,台风涡旋中心围绕着台风观测位置,但扰动后的某些集合成员台风涡旋中心远离观测位置,夸大了台风涡旋中心初始定位的不确定性,影响了台风路径集合概率预报的整体性能,因此发展了台风涡旋中心条件性重定位方案[36]。通过分析2009—2018年中国气象局和日本气象厅最佳台风涡旋中心定位差异,发现10年中年平均值最大为17.18 km(2009年),最小为12.44 km(2010年),结合集合预报模式分辨率,确定了以15 km为临界阈值,判别是否对集合预报成员台风涡旋中心进行重定位处理,即如果集合成员初值场中台风涡旋中心与最佳路径距离差值大于15 km,则判断该集合成员初始场中台风涡旋中心定位超出分析不确定性范围,需要对该成员进行涡旋条件性定位处理,否则认为该集合成员台风涡旋中心不确定性在分析误差范围之内,不进行涡旋重定位处理。重定位方法采用美国地球流体动力试验室(Geophysical Fluid Dynamics Laboratory,GFDL)发展的台风涡旋分离技术[37],对需要进行重定位的台风集合预报成员进行台风初始场与台风涡旋的分离,将分离出的台风部分通过插值平移至观测位置。

表2 GRAPES-REPS和T639-GEPS初值扰动能量谱曲线的交叉尺度[20] Table 2 Intersection scales of the IC perturbation power spectra for GRAPES-REPS and T639-GEPS [20]
3 GRAPES模式随机物理扰动方法
仅使用初值扰动的集合预报系统存在集合成员不够发散、集合预报系统可靠性不足的缺陷[28],因而有必要在GRAPES-GEPS系统中引入模式扰动技术,以表征由于模式误差或模式本身缺陷而造成的不确定性。下面简要介绍应用于GRAPES全球和区域集合预报业务系统的SPPT和SKEB模式扰动方案。
3.1 随机物理过程倾向项扰动方案(SPPT)
随机物理过程倾向项扰动方案(SPPT)的基本思想是对模式物理过程参数化产生的总净倾向项进行随机扰动,以体现模式物理过程参数化所造成的随机误差[39]。根据数值预报积分计算过程,模式积分倾向项可分解为非参数化过程(动力过程)积分倾向项和参数化物理过程积分倾向项,则应用SPPT方案扰动后的模式积分倾向项可表示为:
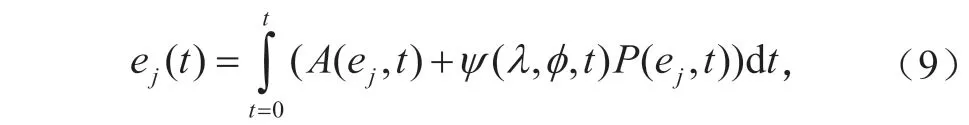
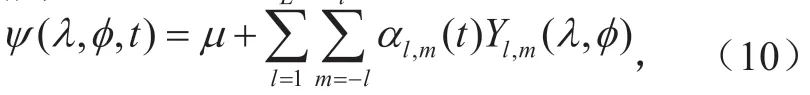
其中:μ为随机场的平均值;λ,φ,t分别表示模式格点经度、纬度和时间;Yl,m为球谐函数;L为随机场的水平截断尺度;l和m分别为水平方向总波数、纬向波数;为随机场谱系数。随机场谱系数在时间维的相关变化特征是通过一阶Markov链随机过程(也称一阶自回归随机过程)来实现[29]。在GRAPES全球/区域集合预报中,均只对位温、水平风分量和湿度预报变量的净倾向项进行扰动。
考虑到全球模式和区域模式积分时间和预报对象不同,SPPT方案在GRAPES全球集合预报和区域集合预报的参数设置有差异。在GRAPES-REPS区域集合预报系统v2.0和v3.0版本中,SPPT扰动幅度取值范围为[0.2,1.8],扰动场均值为1,失相关时间尺度为6 h,最大波数24。在GRAPES全球集合预报中,为了运行稳定性,将随机型函数的扰动幅度取值范围设置为[0.7,1.3],在近地面层和大气层顶处引入倾向扰动垂直廓线,对近地面层和大气层顶附近的物理倾向不进行扰动或者进行较小幅度的扰动。结果表明,在GRAPES全球集合预报系统中引入SPPT方案能显著改进中高纬地区及热带地区的位势高度、温度及风场预报的离散度,特别是对全球集合预报热带地区效果改进更为显著[26,28]。
3.2 动能后向散射随机扰动方案(SKEB)
SKEB方案主要目的是代表模式中次网格尺度能量升尺度转换的随机过程和不确定性[40]。GRAPES全球集合预报的SKEB方案是通过一定时空相关特征的随机型以及局地动能耗散率来构造随机流函数强迫的方式对上述过度耗散的能量进行补偿随机流函数强迫定义如下[30]:



在GRAPES-GEPS v1.0系统中,SKEB方案ψ随机型最小截断波数Lmin为10、最大截断波数Lmax为80、失相关时间尺度τ为6 h、均值μ为0,标准差σ为0.27、最小值ψmin为-0.8、最大值ψmax为0.8。
4 GRAPES全球和区域集合预报业务系统及预报性能
4.1 GRAPES 全球集合预报业务系统
表3是GRAPES-GEPS全球集合预报系统与T639全球集合预报参数设置对比。与T639全球集合预报系统相比,GRAPES-GEPS全球集合预报系统主要的变化包括:初值扰动方法从BGM方法改变为奇异向量方法,模式扰动方法从SPPT改变为SPPT和SKEB方法,台风涡旋处理方法从涡旋重定位和强度调整及时改变为热带气旋奇异向量扰动方法,控制预报初值采用动力升尺度方法[27],集合预报成员数从15个增加为31个。
一般将500 hPa位势高度场距平相关系数(ACC)达到0.6的天数作为可用预报时效。表4是春(2018年 4月)、夏(2017年8月)、秋(2016年10月)和冬(2017年 12月)4个季节代表月逐日12 UTC预报试验可用预报天数对比,可见,与T639-GEPS相比,GRAPES-GEPS的可用预报时效明显增加,北半球、南半球和东亚区域分别增加了0.3 d、0.8 d和0.5 d,GRAPES-GEPS系统预报效果整体优于T639-GEPS系统,尤其是在南半球地区,这种优势更加明显。
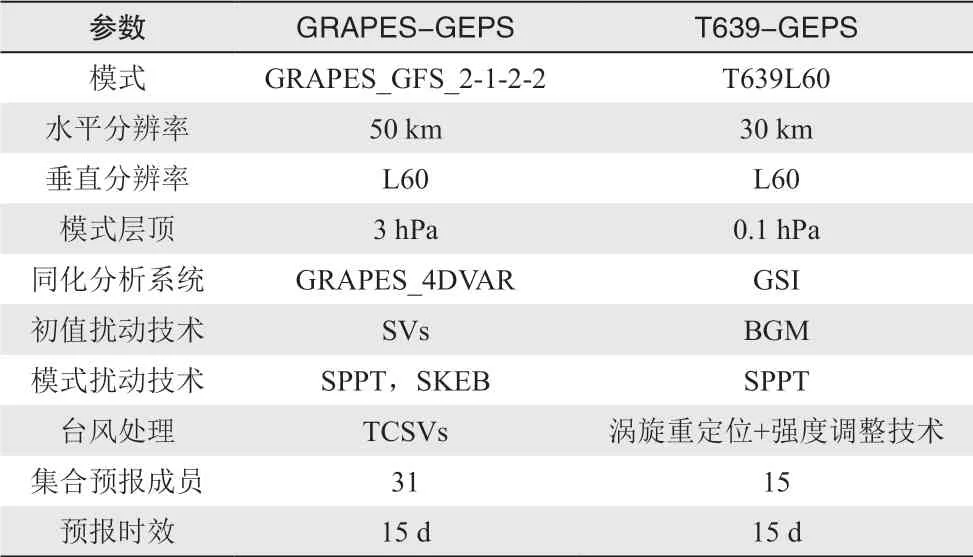
表3 GRAPES-GEPS和 T639-GEPS模式系统参数对比 Table 3 Comparison of Configuration of GRAPES-GEPS and T639-GEPS

表4 GRAPES-GEPS和T639-GEPS集合预报系统可用预报时效(单位:d)[28] Table 4 Available forecast time (days) of the GRAPES-GEPS and T639-GEPS ensemble forecast system (unit: d) [28]
4.2 GRAPES 区域集合预报业务系统
基于GRAPES区域集合预报初值扰动、模式扰动技术研究基础及GRAPES-3km模式云分析技术,开发了以GRAPES全球集合预报为侧边界条件扰动的0.1°水平分辨率GRAPES-REPS区域集合预报系统v3.0版本,2019年9月实现业务化运行。GRAPES-REPS区域集合预报系统v3.0参数配置如表5所示,与GRAPESREPS v2.0相比,主要变化包括:1)集合预报模式水平分辨率由0.15°升级为0.1°;2)初值扰动方法由多尺度混合更新为ETKF初值扰动方案;3)采用了台风涡旋条件性重定位方案;4)模式物理过程扰动方案由GRAPES-REPS v2.0的多物理过程组合+SPPT方案更新为单一物理过程+SPPT方案(详见表6);5)侧边界扰动来自GRAPES-GEPS全球集合预报;6)每个集合成员增加云分析方案,可同化雷达和卫星资料。
图3是2019年7月1日—9月30日GRAPES-REPS v3.0区域集合预报系统与ECMWF全球集合预报系统12 h累积降水的AROC评分对比图。从图可见,GRAPES区域集合预报的小雨、大雨、暴雨前36~48 h预报优于ECMWF全球集合预报,尤其是暴雨各时效均优于ECMWF集合预报,究其原因,可能是在GRAPESREPS v3.0引入云分析方案后同化了雷达资料,36~48 h降水预报较好,而暴雨预报具有优势,可能与GRAPES-REPS模式分辨率较高有关。但GRAPESREPS v3.0中雨预报明显弱于ECMWF集合预报,可能是ECMWF模式对天气尺度系统具有更好的预报能力,雨区或者雨带预报优于GRAPES-REPS。 体现了高分辨率区域集合预报描述强降水预报不确定性的优势。

表5 GRAPES区域集合预报业务系统v3.0及v2.0参数对比 Table 5 Comparison of configuration of GRAPES-REPS v3.0 and v2.0
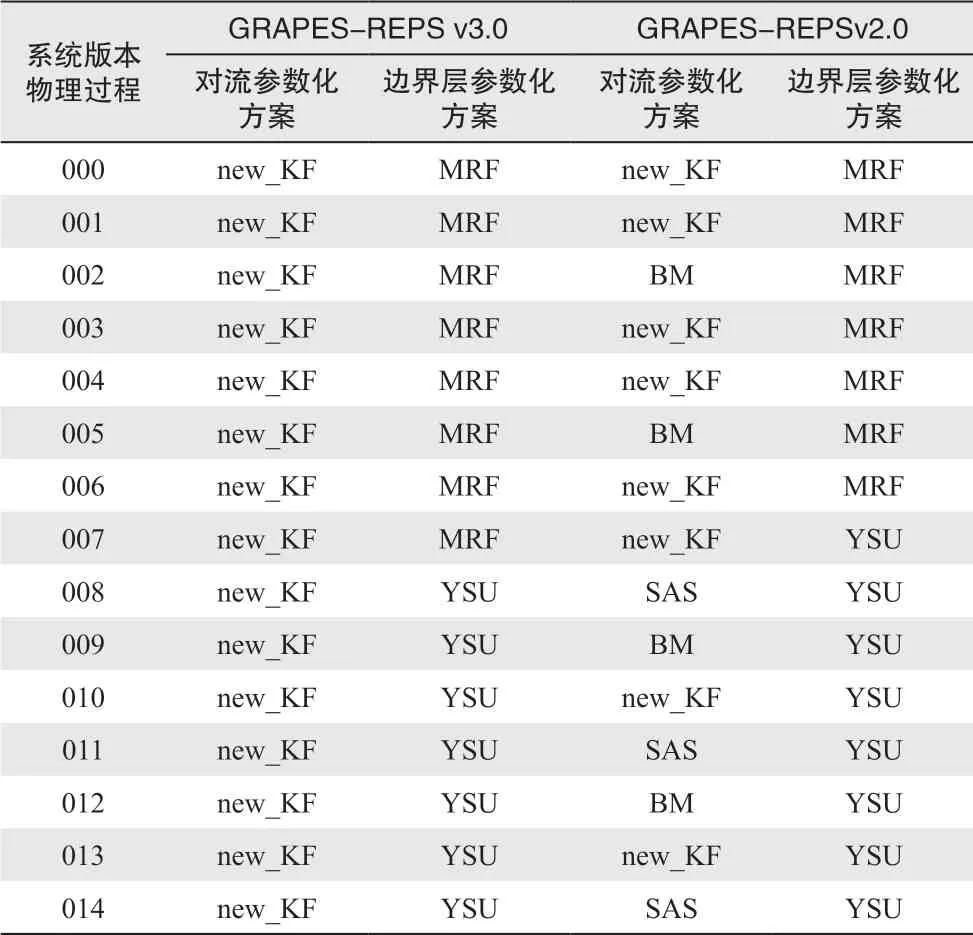
表6 GRAPES区域集合预报业务系统v3.0及v2.0物理过程参数化方案对比 Table 6 Comparison of physics parameterization schemes of GRAPES-REPS v3.0 and v2.0
5 总结及讨论
集合预报是当代数值预报的核心业务系统,本文较系统地概述了中国气象局GRAPES全球/区域集合预报系统发展历程与核心技术方法,回顾了GRAPES全球集合预报奇异向量初值扰动方法、GRAPES区域集合预报集合变换初值扰动方法和多尺度混合初值扰动方法、描述GRAPES全球/区域集合预报模式不确定性的随机物理过程倾向项扰动方法和动能后向散射随机补偿方法研究成果,介绍了GRAPES全球/区域集合预报系统构建参数设置和预报性能,总结如下:

图3 GRAPES-REPS v3.0区域集合预报系统(蓝色),ECMWF全球集合预报系统(红色)12 h累积降水AROC评分 (a)小雨,(b)中雨,(c)大雨,(d)暴雨 (统计时段为2019年7月1日—9月30日,每日两个起报时次:00 UTC和12 UTC,共计64时次) Fig. 3 Comparison of the probabilistic precipitation forecast skills of the GRAPES-REPS v3.0 and ECMWF in terms of AROC (a) >0.1 mm, (b) > 5 mm, (c) >15 mm, (d) >30 mm (The 64 forecasts from 00:00 UTC 1 July 2019 to 12:00 UTC, 30 September 2019 totally are verified)
1) 在代表GRAPES全球集合预报初值不确定方面,发展了GRAPES全球集合预报奇异向量初值扰动技术,构建了热带外中高纬度奇异向量计算方案和热带气旋奇异计算方案。基于高斯分布线性组合奇异向量,构建集合预报初值扰动三维结构,并在初值扰动构造中引入演化奇异向量,使得初始扰动场包括更稳定和较大尺度的扰动信息。
2)在代表GRAPES区域集合预报初值不确定方面,发展了GRAPES区域集合预报集合变换卡尔曼滤波初值扰动方法和多尺度混合初值扰动方法,发展了区域集合预报台风涡旋条件重定位方案,提升中尺度天气系统和台风中心定位初始不确定性的合理性。
3)在代表GRAPES模式不确定性方面,基于一阶马尔科夫链随机过程,开发了GRAPES随机物理过程倾向项扰动方案SPPT和随机动能后向散射补偿方案SKEB,考虑到全球模式和区域模式积分时间和预报对象不同,确定了业务化应用的全球集合预报和区域集合预报的参数值。
4)2018年11月28日,GRAPES全球集合预报系统(GRAPES-GEPS v1.0)实现业务运行,预报效果优于T639全球集合预报系统,北半球、南半球和东亚区域分别增加了0.3 d、0.8 d和0.5 d。2019年9月,基于GRAPES全球模式为侧边界条件扰动场的0.1°水平分辨率的GRAPES区域集合预报系统(GRAPES-REPS v3.0)实现业务运行,该系统侧边界扰动不确定性由T639全球集合预报更新为GRAPES-GEPS全球集合预报,2019年主汛期检验表明,48 h预报时效的降水AROC评分优于ECMWF全球集合预报降水。
尽管GRAPES全球/区域集合预报取得了进步,但仍然存在诸多问题,对这些问题进行初步分析,主要包括:
1)GRAPES-GEPS和GRAPES-REPS的集合预报在预报后期存在离散度-技巧关系不足的问题,离散度低于均方根误差,其中一个可能原因是模式存在较强的系统性偏差[41-43],这导致预报存在较大的均方根误差,需要对此进行深入的诊断分析,认识产生离散度-技巧关系不足的原因,更好地改进离散度-技巧关系不足。
2)造成GRAPES-GEPS和GRAPES-REPS的离散度-技巧关系不足的另一个可能原因是模式随机物理过程随机型函数对不同尺度模式物理过程的随机性代表性不足,当前代表GRAPES模式不确定性的随机物理扰动方法的随机型函数采用的是单一尺度随机型函数,而天气过程是多尺度系统相互作用影响所致,需要增加扰动幅度和多尺度随机信息。
3)在代表初值不确定性方面,当前的GRAPES全球集合预报和区域集合预报与资料同化结合不够紧密,GRAPES全球/区域集合预报的SVs和ETKF初值扰动方法主要是寻找在大气相空间中增长最快的扰动,但对观测误差结构考虑不足,特别是对代表中小尺度信息观测资料的不确定性描述不足。
4)GRAPES全球集合预报在热带外地区的奇异向量采用干物理过程切线性模式,不能很好地代表湿物理过程误差增长特征,加之GRAPES全球和区域集合预报分别采用奇异向量初值扰动方法和集合变换初值扰动方法,增加发展成本,不利于在GRAPES初值扰动方面开展深入工作。
6 未来展望
未来GRAPES全球/区域集合预报未来将重点关注如下四个方面:
1)发展GRAPES无缝隙集合预报(Seamless ensemble)。无缝隙集合预报包括了两方面含义:一方面,各数值预报中心从对流尺度短临数值预报、全球中期数值预报、延伸期和气候预测模式均采用集合预报技术,构建从短时临近、中期和延伸期的GRAPES无时空缝隙集合预报;另一方面,集合预报系统与高分辨率模式采用统一分辨率并与资料同化系统耦合发展,集合预报为同化系统提供“流依赖”的背景误差协方差,同化系统为集合预报提供初值不确定信息和扰动场,构建无缝隙数值预报模式体系。ECMWF计划2020年将18 km分辨率全球集合预报和9 km分辨率高分辨率模式统一为9 km全球集合预报系统,采用集合变分资料同化方法(EDA)来估计“流依赖”背景误差协方差和初值扰动,美国环境预报中心(NCEP)发展了集合卡尔曼变分同化系统。GRAPES全球/区域集合预报技术与同化系统耦合发展也将成为必然选择。
2)发展GRAPES对流尺度集合预报技术。国际集合预报业务系统正走向对流尺度。一是为满足局地强对流突发灾害预报预警需求的百米—千米级有限区域集合预报在西方发达国家已经成为核心业务,如美国的超级对流集合系统(CLUE:Community Leveraged Unified Ensemble),英国的MOGREPSUK(2.2 km,12个成员)、德国的COSMODE-EPS (2.8 km,20个成员)和法国气象局的AROME-EPS (2.5 km,12个成员)等,二是全球集合预报系统对流尺度化也是未来发展趋势,ECMWF宣称2025年战略目标是建立5 km水平网格距的全球中期确定性和集合预报一体化系统。GRAPES区域集合预报将更侧重于描述对流系统的不确定性。
3)发展GRAPES多尺度随机物理扰动方法。集合预报技术更加关注数值预报模式的随机误差代表性,强调发展适用于不同时空尺度集合预报和同化分析的多尺度随机扰动技术,尤其是热带地区,如何预报和模拟热带对流系统的不确定性,必须改善GRAPES物理过程扰动方法、海气耦合及相互作用的不确定性。
4)发展集合预报误差诊断包,检查离散度-技巧比率的空间分布,以及点对点的误差-离散度关系散点图,进一步理解分析具体系统性误差结构,方便集合预报系统的离散度-技巧比率改进方法及模式随机物理扰动方案调试。
最后需要说明的是,对于GRAPES全球/区域集合预报研究及应用方面的问题和未来展望,是作者在GRAPES全球/区域集合预报研究开发和业务应用过程中的浅薄体会和一孔之见。同时,受篇幅限制,GRAPES全球/区域集合预报尚有许多重要方面,如随机参数扰动、概率预报后处理等未有涉及。
 Advances in Meteorological Science and Technology2020年2期
Advances in Meteorological Science and Technology2020年2期
- Advances in Meteorological Science and Technology的其它文章
- 主编语
- 气象部门政府购买人才服务需求探讨
- 新时代气象科普工作的定位与可持续发展路径研究
- 浅析气象继续教育教案的编写
- 冠层垂直变化的高分辨率激光观测
- AMS词汇
