在多维空间讨论利息
——对建构“经济学统一场”的场方程的思考
陈 勇 勤
(中国人民大学 经济学院,北京 100872)
古希腊的亚里士多德在“被视为一本经济学”的《政治学》中写道,“钱贷”或“放债”是“从作为交易的中介的钱币身上取得私利。为了交易方便人们使用货币,而钱商竟然强使金钱增殖。这显示了希腊人常说的‘子息’这个用词的真意……本钱诞生子钱,所谓‘利息’正是‘钱币所生的钱币’。由此我们可以认识到,在致富的各种方法中,钱贷确实是最不合乎自然的”[1]10,13。英国学者配第在1690年出版的《政治算术》一书中提道:“贷款的利息,在50年前每百磅为10磅,40年前降为8磅,现在则跌至6磅。但是,利息的降低却不是任何为这个目的而制定的法律所造成的,现在只要有有利的担保,便能借到利息更低的贷款,因为利息的自然降低是由于货币增加的结果。”[2]74配第把利息看作货币的租金。同时期另一位英国学者诺思把利息看作资本的租金,认为利息高低取决于借贷资本的供求量。18世纪英国学者中,马西认为利息取决于利润,休谟认为利息率高低与货币数量无关,斯图亚特认为利息率差异会影响金银在国际间的流动。同时期法国学者杜尔哥从“有息借贷只是一种商业交易”角度认为,利息高低取决于有关双方自由协议。18—19世纪英国经济学家中,斯密和李嘉图对利息论述都不多,但一致认为利息率取决于利润率。在18世纪意大利学者加里阿尼的利息即“贴水”基础上,19世纪后期奥地利经济学家庞巴维克提出“时差利息论”。
如果说开创微观经济学的19世纪末20世纪初英国经济学家马歇尔并未特别关注利息(“古典学派的利息率理论……它是哺育我们所有这些人的,而且直到最近我们还无保留地予以承认的经济思想……在马歇尔的《经济学原理》里,找不到像以上那样直截了当的说法。”[3]161-162),那么开创宏观经济学的20世纪前期英国经济学家凯恩斯则表现出对利息非常重视。我们的讨论就从这里开始。
一、利息率与储蓄量、投资量
凯恩斯的名著《就业、利息和货币通论》在1936年出版,书名中就醒目地直接点出“利息”。在第十四章“古典学派的利息率理论”里,凯恩斯谈道:
古典学派的传统把利息率当作一个使投资的需求与储蓄的意愿彼此达到均衡的因素。投资代表对投入资源的需求,储蓄代表可投入资源的供给,利息率则是能使这二者相等的可投入资源的“价格”。正像商品的价格一样,它决定于对它的需求与对它的供给相等之点。利息率也必然会在市场力量的作用下使投资量与储蓄量相等之点。[3]161
不同于相信储蓄和投资实际上是能够不相等的新古典学派,古典学派则接受了二者相等的观点……一致之处,可以概括为古典学派会接受而我也不会反对的一个命题,即:假设收入水平是既定的,那么,我们可以推断说,现行的利息率必须处于一点,在该点,相应于不同利息率的资本需求曲线与相应于不同利息率的既定收入的储蓄量曲线相交。[3]164
但是,正是在这点上,确定的错误的东西就慢慢进入到古典学派的理论中了……古典学派的理论不仅忽视了收入水平变化的影响,而且还包含有条理上的错误。[3]164-165
古典派的利息率理论似乎假定:如果资本需求曲线移动,或者体现利息率对既定收入中储蓄量的关系的曲线移动,或者这两条曲线同时移动,则新的利息率就由这两条曲线的交点的新的位置来决定。但是,这是一个荒谬的理论,因为该理论所假定的收入不变和它关于两条曲线能够相互独立地移动的假设是矛盾的……这种假设顶多只能适用于与长期均衡有关的情况,而不能形成短期理论的基础;甚至在长期中,也没有理由认为,这种假设能够成立。真实情况是:古典学派理论并没有想到收入水平的变化所起的作用,或者没有意识到收入水平实际上是投资量的函数的可能性。[3]165-166
古典学派理论所使用的函数:投资量对利息率的变动的反应与既定收入下的储蓄量对利息率的变动的反应,都不能为利息率理论提供所需要的材料。但是,它们能够被用来告诉我们:在既定的……利息率条件下,收入水平将如何;或者换另一种说法,即:如果收入被保持在一个既定的水平……利息率将如何。
古典学派的错误来源于把利息率当作等待的报酬,而不是把它看成不贮藏货币的报酬。[3]167
传统的分析是错误的,因为它未能把经济体系的自变量正确地隔离出来。储蓄和投资是由经济制度所决定的因素,而不是决定经济制度的因素。它们是经济制度的决定因素所导致的后果。这些因素是:消费倾向,资本边际效率表和利息率。这三个因素本身的确是复杂的,而且每一个因素都会由于其他两个因素的未来的变化而受到影响……它们仍然是自变量。传统的分析知道储蓄取决于收入,但却忽略了收入取决于投资的事实。其形式是:当投资改变了,收入必然改变,改变的程度是能使储蓄的变化等于投资的变化。
重要的结论是:新投资的产量将会推进到一点,在该点,资本的边际效率将等于利息率;而资本边际效率表告诉我们的不是利息率如何,而是在既定利息率条件下,新投资的产量将被推进到那一点。
这里所讨论的问题具有最基本的理论意义和头等的实践重要性,因为经济学家们赖以对实际问题提出建议的经济学原理,总是设想:假定其他条件不变,消费减少,利息率会趋于下降;投资增加,利息率会上升。但是,如果上述二者所决定的不是利息率,而是就业总量,那么,我们对经济体系运行机制的看法将会有深刻的变化。因为在其他条件不变的情况下,如果把消费愿望的减退不当做增加投资的因素,而当做减少就业量的因素,这就代表着对消费愿望减退的看法有着很大的分歧。[3]169-170
凯恩斯提醒学界同行们注意,投资与消费的反比关系,既有可能决定利息率,又有可能决定就业量。这正是《就业、利息和货币通论》的书名中也醒目地直接点出“就业”的原因之所在。
二、多个变量与多维空间
二元及二元以上的函数统称为多元函数,但二维被单称为平面,而三维及三维以上的空间统称为多维空间。
三元函数对应于三维空间。以此类推,n+2元函数对应于n+2维空间。
空间解析几何中,如果把曲面看成是满足某些条件的空间动点的轨迹,那么在空间直角坐标系下,可以建立空间曲面与包含3个变量的三元方程F(x,y,z)=0的对应关系,也可以建立空间曲面与包含多个变量(大于3个变量)的多元方程F(x,y,z,t,…)=0的对应关系。
如果把曲面看成是满足某种条件的空间动曲线的轨迹,那么上述对应关系也成立。
理论物理学在试图“统一所有已知的物理现象”方面提出了超空间理论或Kaluza-Klein理论、超引力理论、超弦理论,都是针对高维空间的假说。
三、利息的三个近似理论与数学方法
美国经济学家费雪在1930年出版的《利息理论》一书中,给出利息的三个近似理论和相关的数学方法。利息的第一近似理论“假设每个人的收入川流已先预知,除非经由借贷不可改变”[4]88。“没有借贷,因而也不会有市场利率……能够互相交换其收入川流时……无数的时间偏好率或不耐率立即趋向于一个共同的百分率,在交易不带有风险的假定下,事实上某种一律的市场利率将会建立起来。”[4]203对“第一近似理论的几何说明”是,“如果我们把利率问题用图形的方法来表示,则利率的决定可归结为一个简单的几何问题,正如同价格问题可用供给与需求曲线来表示一样”[4]204。对“第一近似理论的公式说明”是,从代数角度,用方程式来表明构成第一近似理论的若干原理,“方程式的解也就是利息问题的解”[4]253。
利息的第二近似理论“假设收入可通过借贷和其他方法进行变更”[4]110。对“第二近似理论的几何说明”是,要特别关注图形中的“投资机会线”[4]231-232。对“第二近似理论的公式说明”是,从代数角度,用方程式“来表明构成第二近似理论的六条原理”[4]266。“公式法的价值,特别是在于确切表明方程式的数目与未知数的数目相等,不用公式法,则决定变数的问题是不能完全解决的。”[4]275
利息的第三近似理论“假设收入不确定”[4]179。然而,第三近似理论“不适于数学表述”。费雪阐述了他的观点:
像利率这样一个受偶然性支配的东西,如果想把决定利率的规律,很有效地、很完整地用数学公式表示出来……这样的公式……不会有多大价值。
在科学中,最有用的公式是应用于最简单情形中的公式。
科学的决定绝不可能百分之百地正确。充其量,科学只能决定在假设的情形下所将要发生的事情。它绝不能准确地说明实际情形中正在或将要发生的事情。
我们必须放弃想完整地表述真正决定利率的各种影响的企图,这是没有用的工作。
搅乱的原因就不能这样单纯合理地予以表述。其中有些可根据经验来进行研究……它们关系到统计学而非纯粹经济学。(这反映出)在经济学中,合理的与经验的规律……我们也可将……利率的实际动向看作是……合理规律与经验上……政策连同无数其他制度的、历史的、法律的与实际的因素所产生搅乱的复合物。
唯一特别重要的搅乱影响是关于不稳定的货币本位……但关于这一影响,理论与实际就大不相同了。不稳定货币的搅乱往往引起那些决定利率的基本力量的反常作用。
经验问题的解决代表应用科学的最高理想。但在达到这一阶段前,合理的科学与经验的科学间仍有很大的距离,而且两者须用多少有些不同的方法来研究。今天经济科学在大多数问题上就是这种情形。[4]279-285
费雪的利息论从研究方法上推动了经济学的发展。在凯恩斯的评论中,他认为,“虽然费雪教授在他的《利息理论》一书中没有使用过‘资本边际效率’这个名词,但他对它称之为‘超过成本的报酬率’下过定义。他的定义……在意义上和目的上和我使用‘资本边际效率’这个名词是完全一样的”[3]128-129。
凯恩斯又指出:“费雪教授原先称为‘增值与利息’理论……这个理论区分了货币利息率与实际利息率,经过货币价值矫正之后,后者等于前者……如果利息率随着资本边际效率的提高而同时相应地上升,那么,就不会有来自预期价格上升的刺激作用。因为对产量的刺激取决于既定资本存量的边际效率对利息率的相对地提高。诚然,费雪教授的理论最好用‘实际利息率’这个概念来重写。实际利息率应该定义为:由于货币未来价值预期的变化而导致的需要加以管理的利息率。管理的目的在于:使这种预期的货币价值的变化不致对现行产量产生任何影响。”[3]129-130
四、利息现象与货币学说
共25卷的《凯恩斯全集》是英国皇家经济学会为纪念凯恩斯而出版的。第7卷的编者在“绪言”中提道:“《通论》的起源在于凯恩斯对他的《货币论》不满”;剑桥大学经济学者的一次聚会讨论,“为《货币论》和《通论》之间演变的最初阶段提供了一定基础”;“最初指示凯恩斯在《货币论》和《通论》之间思想方向的重要出版物出现在1933年”[3]2。这正是《就业、利息和货币通论》的书名中又醒目地直接点出“货币”的原因之所在。
考察“利息和货币的主要性质”,凯恩斯说:“利息率不过是一定数量的货币”[3]206,“货币又是一个追求购买力的无底洞”[3]215。
旨在求解“哈恩难题”的新货币经济学,是货币系统由技术创新到制度创新再到理论创新这一发展路径的产物。仅就“货币数量的扰动性”而言,由于以电子资金转账为特征的无纸化货币使得银行存款“份额”的数量与“计价单位”的数量正在走向分离,所以,在这个机制下,银行存款份额数量——货币数量对经济体系均衡的影响不再重要。即便如此,对“货币数量是利息率的函数”问题的研究不会结束。
五、利息率与汇率
Mundell-Fleming模型是考察价格不变和资本完全自由流动时利息率、汇率、国际收支与国民收入的关系。这个模型包含商品市场均衡式、货币市场均衡式、国际收支平衡式,三者分别写作:
Y=C(Y-T)+I(r)+G+NX(e,Y)
B(e,Y)+K(r)=0
其中,r表示国内利息率,e表示汇率。Mundell-Fleming模型说明,均衡利息率不仅取决于国内产品供求和货币供求,而且取决于汇率和国际收支。
六、利息率与利润率、价格
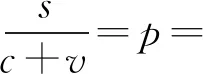
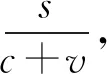
当“货币均衡与一般均衡”成为论题时,瑞典经济学家米尔达尔认为,“货币均衡”与“市场利息率和自然利息率之间的关系”[7]48有关。在“净收益是收益减去成本,收益率是净收益除以收益”[7]60的前提下,米尔达尔说:“货币均衡的第一个条件是实际资本的收益率”,“利息率等于现有实际资本的收益率”[7]25。“在信用市场中,货币利息等于在一单位时期内支配一单位资本的成本。”[7]25
费雪对“利息率与价格”的论证。关于利息率与物价变动,费雪说:“在经济学中,没有别的问题比物价水平与利率关系的问题争论得更热烈了。”[4]351并且认为,“物价水平的预期变动确对货币利率有一定的影响”[4]351。关于利息率与物价变动率,费雪通过对数据的分析研究,指出:“至少在长时期内利率是跟随着物价变动的。”[4]374关于短期利率与物价,费雪说:“物价与利息的变动似乎是受一个规律支配的,而不是像过去认为的那样,短期和长期的变动是受两个对抗的规律所支配。”[4]378关于利息率与物价指数,费雪通过对数据的分析研究,指出“在各长时期内,高或低的利率跟随着高或低的物价跑”;“短期利率与季度指数的比较,没有得到显著的结果”[4]380。
如果说在一定程度上成本决定价格,那么费雪认为“利息作为成本”自然会引起我们注意。费雪指出:“必须用成本才能充分说明利息现象。”[4]430
瑞典经济学家林达尔讨论了“利息率和物价水平”。他说,“货币管理机构对物价水平施加影响所使用的最重要手段,乃是对银行放款和存款厘定利息率”[8]132;“利息率作为保持稳定的物价水平的工具”[8]165,“利息率作为调整物价使其和生产力成反比例的工具”[8]184。
七、利息率与金融制度
我们知道,金融制度的变化会通过改变持币成本而影响人们的持币行为。而且,刻画这种变动的变量是利息率。
林达尔说:“利息率政策可能包括两个方面:调整一般利息率,把它提高或把它降低;对各种存款放款厘定有差别的利息率。”[8]132
对于“利息率与银行准备”,费雪说:“在正常的情形下,银行对利率所起的作用,只不过是传播收入川流的影响。假如我们能够科学地调节银行准备的根本来源,即世界上对货币黄金的供给,则实际情形基本上也就是这样的。如果世界黄金供给能加以调节,使得那些黄金的购买力从而货币单位的购买力能保持不变的话,我们就能依靠银行适当地,即或是不自觉地,调节利率使之适合于一国的收入情况。”[4]397-400但“不幸的是,我们还没有这样科学的通货制度,我们仍然遭受金融市场上每次风波的袭击”[4]397-398。
关于“制度对利息率的影响”,费雪说:“如果我们一开始时便假定,在货币或信用经济中对货币借贷所确定的市场利率,是唯一存在的利率,我们就面临一个问题,需要说明为什么会有这样的利率存在。制度本身不能说明它……制度与习俗是人们创造出来的……制度不能使人们的言行有所异于人。人所建立的和运用的制度,只不过是人所设计的一些工具,用来为他取得更容易、更丰富的满足罢了……法律、黄金移动、证券交易所投机、银行惯例与政策、政府财政、公司实务、投资信托以及许多其他因素对所谓金融市场都发生一定的影响,而利率就是由金融市场决定的。”[4]434-435
八、利息与超空间场和数学工具
如果说理论物理学有一个“爱因斯坦梦寐以求的‘物理学圣杯’统一场论”,那么理论经济学或许也有一个“‘经济学圣杯’统一场论”。当然,经济学的“场”指经济社会中可数字化的力的集合。这个“场”以人为中心,人又以“群”存在。多样化、有思维的人力,多样化、可使用的物力,次序性、可计量的时间,三者是“经济学统一场”的基本元素。
场论是物理学的语言,由19世纪英国科学家法拉第首先引入。“简单地说,场就是定义在空间每一点的数字的集合。这些数字完整地描述了所对应空间各点的力。”[9]29也可以说,“自然界所有的力都能被表述为场的形式”[9]29。
我们构思的“经济学统一场”,它所针对的是“五维空间的经济社会”。其中,有四维是客观存在的,有一维是根据自然界的客观存在而科学设定的。客观存在的四维中,有两维是各自可以独立存在的,有一维是具有“由内向外”因素从而非独立存在的,有一维是具有“由外向内”因素从而非独立存在的。此外,科学设定的一维也是可以独立存在的。
对应于我们假设的“五维空间的经济社会”,具体还有:四维常时空,五维超时空。不过要注意,这里的“四维”不是前面说的“客观存在的四维”,而是“常时空的四维”,它包括“各自可以独立存在的两维”“具有‘由内向外’因素从而非独立存在的一维”“科学设定的一维”。显然,在这一基础上,“超时空的五维”就是“常时空的四维”加上“具有‘由外向内’因素从而非独立存在的一维”。
“事实上,由于进化的原因,我们不可能目睹更高的维数。我们的大脑已经进化到能在三维之中处理大量的紧急事件……遗憾的是,人类并没有需要把握在四个空间维度中运动的生存压力。”[9]13对此,正如一位美国物理学家所言,由于“不能形象化地描述高维空间”,所以只能“退到了数学方程的世界中”,这表明“我们充其量只能利用数学技巧来一睹高维客体的影子”[9]13。
如果说“自然规律在高维空间表述时会变得更为简单和优美”,“统一自然规律的关键步骤是增加时空的维数,从而能合理安排越来越多的力”,“在更高维中,我们有足够的‘空间’来统一所有已知的物理力”;那么也可以设想,经济社会的客观规律“在高维空间表述时会变得更为简单和优美”,“统一”经济社会的客观规律的“关键步骤是增加时空的维数,从而能合理安排越来越多的力”,“在更高维中,我们有足够的‘空间’来统一所有已知”的经济力[9]14。
“高维空间的发现最早开始于数学家黎曼。黎曼预料到科学在下一个世纪的发展,首先陈述了他的见解:大自然在高维空间几何学中找到它的天然归宿。”[9]1可以说,“黎曼工作的核心是使物理定律在高维空间的简化得以实现”[9]1。黎曼在1854年发表的《论奠定几何学基础的假说》一文中提出:“建立多维量的概念”,“建立n维流形的概念”,对应“曲率”并“用曲面来几何地描述”“n维流形中的度量关系”[10]243-253。
“对于黎曼而言,‘力’是几何的结果。”同时,“黎曼推断,电、磁和引力皆由我们的三维宇宙在看不见的第四维中起皱所致。因此,‘力’本身并不存在,它只是几何畸变引起的明显结果。通过引进第四个空间维,黎曼意外地发现自然规律在高维空间中表述时显得简单了……他就着手研究能够表述这种思想的数学语言”[9]43。进一步,“黎曼的思想是在空间的每一点引进一组数,这组数将描述空间在这一点被挠曲或弯曲的程度”;“黎曼发现,在四维空间,人们需要在每一点引进一组10个数来描述它的性质。无论这个空间被弄皱或扭曲成什么样子,在每一点的一组10个数已足以表达该空间的所有信息……这个数组被称为黎曼度规张量”;“黎曼的度规张量使他建立了一种强有力的工具来描述具有任意曲率的任何维空间。他惊奇地发现,所有这些空间都能明确定义,而且也很自洽”[9]43。有待后人来完成的一个问题是,如何知道“为了产生引力,宇宙将被怎样弄皱”,如何计算“为描述各种力而必须使空间褶皱多少”。总之,“黎曼运用几何学即‘褶皱的超空间’来解释‘力’的本质”,“利用法拉第的场概念或黎曼的度规张量去寻求超空间所遵循的场方程”[9]43。
对于经济学来说,同样负有“寻求超空间所遵循的场方程”这一任务。至于利息,它不过是“经济社会超空间场”中一个力当中的一个分量(分力)而已。尽管“利息在经济学中的地位”已被明确为:“利息在价值与价格理论中以及在分配理论中都起着重要的作用。在财富、财产与服务的价值(或价格)决定中,利率是根本不可缺少的。”[4]289
有两个我们并不陌生的场方程。其中的一个,即:
另一个,即:
这是物理学的场方程。我们注意到它,是因为对我们建构“经济学统一场”的场方程,或许有一定的启示作用。

