基于线性自抗扰控制的高频真空感应炉温度控制

付 莹，李冰玉，郭继宁，2

（1.渤海大学，辽宁锦州 121013;2.东北林业大学，黑龙江哈尔滨 150040）

1 背景

真空感应炉是在真空条件下，利用电磁感应在金属导体内产生涡流加热炉料进行熔炼，并用下连铸机构拉铸金属的现代化设备。随着航天航空、原子能、军工等尖端科学技术的迅速发展，真空冶金技术在稀有金属、钢和特种合金的冶炼方面的应用日益广泛，且自动化水平越来越高。在实际生产过程中，炉体温度、炉内压强、真空度等因素对产品性能都有不同程度的影响，其中温度是真空冶金中重要的参数之一。为了使生产效率尽可能的提高，就必须对生产过程中出现的温度进行有效的控制，使真空感应炉内的温度保持在金属熔点之上并达到电热效率最大化。由于温度升高对物料电阻率的影响以及物料本身产生的热辐射等现象都对系统温度控制精度有一定的影响，且反应过程难以预测，这使真空感应炉具有很强的非线性、时滞特性以及不确定性[1，2]。对于具有大时滞、非线性、不确定性的复杂系统很难建立起精确的数学模型，限制了现有的控制理论在实际工程中的应用。许多专家学者将复合PID 控制方法应用到系统中。路桂明用模糊PID 的方法控制电锅炉内的温度，使系统的调节时间缩短、稳态误差变小，但模糊PID 控制算法不够完善，不能很好的运用于实际工程中[3]。滕宁宁采用Smith 预估器和模糊PID 控制相结合的方法对电加热炉的时滞问题进行补偿，使系统具有较强的鲁棒性和抗干扰能力，但并没有具体的设备进行实验，所设计的控制系统会存在一些问题，有待改进[4]。李英顺提出了一种基于遗传算法的PID 控制方法对真空感应炉的温度进行控制，利用遗传算法获取最优的PID 控制参数，但仍然是一种基于模型的控制算法，不能从根本上解决系统模型不确定性的问题[5]。韩京清先生在经典PID“基于误差消除误差”的理论基础上创立自抗扰控制理论[6]。自抗扰控制器（Active Disturbance Rejection Controller,ADRC）可以将被控对象中出现的各种不确定因素归结为总扰动，利用扩张状态观测器对系统进行实时估计，并将系统补偿为串联积分器标称模型的基本形式[7]。近年来，自抗扰控制影响力与日俱增，在工程领域也得到了广泛应用。自抗扰控制器由非线性状态误差反馈（Nonlinear State Error Feedback）、扩张状态观测器（Extended State Observer）和微分跟踪器（Tracking Differentiator）三个部分组成[8]。其中扩张状态观测器以及误差反馈控制都是以非线性函数呈现的，理论分析具有较大难度，待整定参数较多，不利于实际应用。对此高志强教授将以上两个环节进行线性处理，提出了线性自抗扰控制器（Linear Active disturbance rejection controller,LADRC），并利用带宽来确定控制器的参数，使系统更加适合实际应用[9，10]。

本文针对真空感应炉的温度控制问题，设计了线性自抗扰控制器。运用劳斯判据证明了系统的稳定性，并用双轨迹法分析了控制系统的稳定域，使观测器能更好的估计总扰动。最后，用MATLAB 仿真实验证明了系统的鲁棒性和抗干扰能力。

2 真空感应炉工艺

真空感应炉是一种将金属置于真空环境中利用高温加热进行冶炼及提纯的熔炼设备[11]。不同金属元素的挥发温度不同，因此熔炼的温度直接影响着合金的成分。经过真空感应炉热处理的金属材料可提高韧性、耐腐蚀性等多种性能。真空感应炉分为电源输入系统、真空系统以及炉体三个部分。真空条件下的碳元素具有很强的脱氧能力，这就避免了使用金属脱氧剂进行脱氧产生的污染问题。真空感应炉中的坩埚封闭在真空室中，利用高频电源通过感应线圈并在感应线圈内部产生交变磁场，线圈内部的被加热物料的表面就会产生涡流，以达到对物料加热的效果。感应加热的过程分为电磁感应过程和热传导过程。其中电磁感应过程是主要的加热方式。热传导过程中所需要的能量实际上是由电磁感应过程中所产生的涡流功率提供的[12]。

感应加热原理图和高频真空感应炉实物图如下所示。

图1 感应加热原理图

图2 高频真空感应炉实物图

2.1 真空感应炉控制系统模型

真空感应炉在控制熔炼的过程中，控制对象为感应炉，执行机构是高频电源，用热电偶测温的方法来测量坩埚内温度。控制系统的输入输出值均为温度。其控制系统结构图如图3 所示。由于系统的时滞性、非线性以及不确定性，很难建立精确的数学模型。在实际工程中，基于其“温度飞升”曲线，可以将感应炉近似看作是带有纯滞后环节的一阶系统[13]，其传递函数为：

图3 真空感应炉的温度控制结构图

式中 G（s）——传递函数；

K——控制对象的静态增益；

T——控制对象的时间常数；

τ——为控制对象的纯滞后时间；

s——频域变量。

2.2 一阶时滞系统的模型辨识

本实验在真空感应热处理炉上进行了数据采集，当频率为5141Hz 时，每间隔30s 记录一次温度的变化情况。将采集到的数据，用最小二乘法进行模型参数辨识，拟合度达到93.93%，拟合结果如图4 所示。

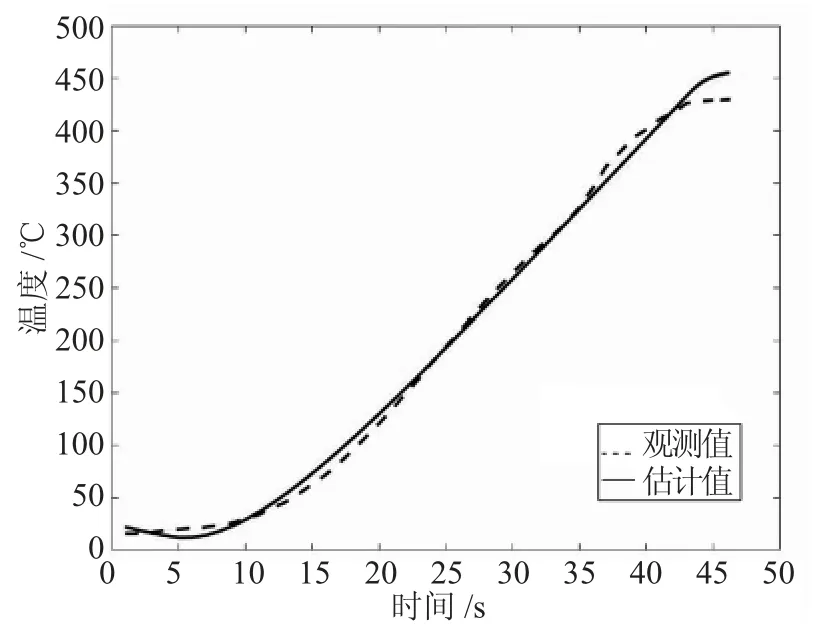
图4 系统模型辨识

3 线性自抗扰控制系统

线性自抗扰控制是在自抗扰控制的基础上，将自抗扰控制的主要环节进行线性化处理后得到的。LADRC 具有结构简单、易于分析和待整定参数较少的优点。LADRC 的核心环节为线性扩张状态观测器（LESO），是用来对系统总扰动进行实时估计并在线补偿。如图5 所示，为一阶线性自抗扰控制的结构框图。

对于具有时滞系统的线性自抗扰控制，先将式(1)中的时滞环节近似为1[8，14]，不含时滞的一阶被控对象可用微分方程表示为：

图5 一阶线性自抗扰结构框图

式中 y（t）、u（t）——系统的输入量和输出量

d——由于物料加热产生的辐射损失[12]；

f（·）——系统的总扰动；

b——系统的时滞增益[14]。

当b 和b0近似相等时，原系统有可以简化为式（3）所示的串联积分的形式：

其中一阶自抗扰中的虚拟控制量u0可选择为比例控制，即

无时滞系统的一阶惯性环节,可表示为：

若将惯性环节转化为状态方程,可表示为：

式中 x1——被控系统温度；

x2——加热过程中由于物料产生的热辐射而导致的辐射损失。

为了方便分析，式（6）也可以用矩阵形式表示为：

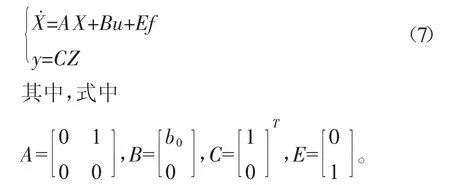
可将相应的二阶线性扩张状态观测器（LESO）设计为式（7），用来估计被控系统的总扰动：

L=［β1β2］T——LESO 的观测器增益；

b0——时滞增益b 的估计值。

可将线性误差反馈控制率（LSEF）设计为：

综上所述，线性自抗扰的可调参数有kp，ω0和b0。而且不需要知道扰动和被控对象的精确模型，很大程度上减少了控制系统中参数调节的时间。用带宽法对以上参数进行整定[15，16]，则L=[2ω0ω02]，kp=ωc，ωc是控制器带宽，根据观测器设计的经验公式ω0=3ωc～5ωc[17]。故只需要对ωc进行选取。根据试凑法，当ω0=3ωc时，被控系统动态性能最佳。

4 稳定性分析

在实验室真空感应热处理炉收集数据，并用MATLAB 进行系统辨识，得到控制对象的一阶时滞系统的数学模型为：

为了方便稳定性分析，将图4 转化为传递函数的形式，如图6 所示：

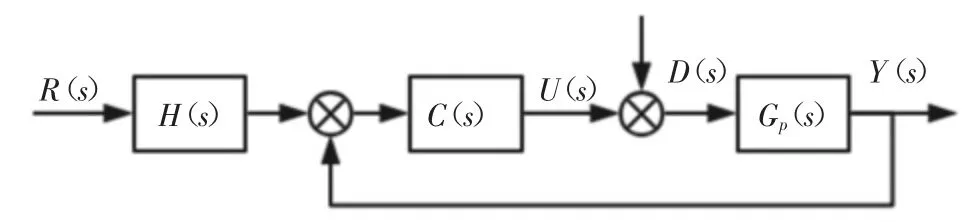
图6 一阶线性自抗扰传递函数框图

其中R（s）是参考信号，Y（s）是输出信号，D（s）是扰动信号，U（s）是控制量信号，Gp（s）是被控对象模型，H（s）和C（s）为控制器的待定项。由图5可知：

将式（4）代入式（9）做拉式变换，再对式（8）做拉式变换，可得控制器参数H（s）和C（s）分别为：

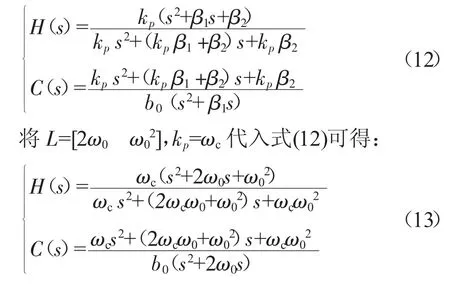
可得系统的闭环传递函数为：

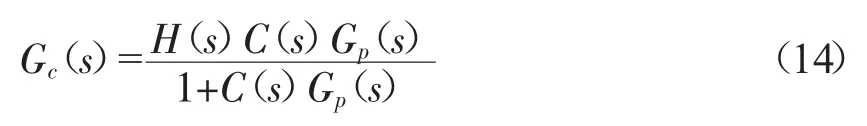
将ωc代入式（14）可得系统的特征方程为：

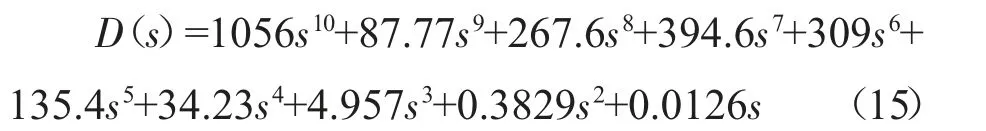
由劳斯稳定判据可得劳斯表，如表1 所示。

表1 劳斯表

由劳斯判据可知，劳斯表中左端第一列元素全为正[18]，则可判定系统是稳定的。

5 仿真分析

5.1 稳定域边界分析

对于一阶时滞系统，可用双轨迹法对参数稳定域进行分析[17]。对于一阶时滞系统的一阶线性自抗扰控制的稳定域分析定理如下：当对象参数中的稳态增益K、时间常数T1、滞后时间τ、以及观测器带宽和控制器带宽之比k 给定时，系统满足存在一个正实根，且开环传递函数无右半平面极点时，若满足则系统是稳定的，且稳定域为θ={ωc｜ξ1-ξ2＞0，τ，T1，K，k}。

式中 ξ1、ξ2——L（jωi）和-ejωτ在交点处的相；

ωi——-ejωτ的交点频率。

可得到如下方程：

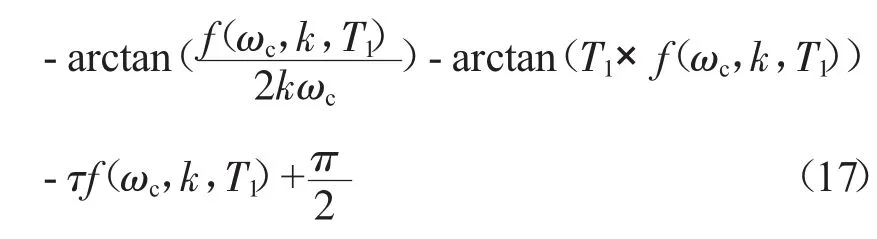
当其他参数给定时，可从式（13）看出方程的未知量只与ωc有关，稳定域为θ＝（0，ωc*）。从式（10）可知K=13.5，T1=6.5，τ=3.1，取k=5。由式（11）可得ωc*=0.3。观察ωc在稳定域内的单位阶跃响应。

图7 可以看出，输入为阶跃响应时，ωc只要选取（0，0.3）的范围内都能保证系统稳定。当ωc=0.1时系统的调节时间超过了350 秒；当ωc=0.2 时在100s 左右到达稳定状态；当ωc=0.27 时系统稳定到了1.04 左右；故选取ωc=0.25 时，系统调节时间短，响应速度更快。

图7 ωc 的选取

5.2 跟踪性能分析

用Z-N 法对PID 控制器进行参数整定，选定LADRC 中的参数为ωc=0.25，在此条件下比较PID控制和LADRC 控制的鲁棒性。在系统运行300s时加入脉冲扰动模拟由于加热产生的热辐射而导致的辐射损失，比较两种控制下的抗干扰能力。由图8 可知，LADRC 相较与PID 控制有更快的调节时间。如图9 所示当系统存在扰动时，LADRC 中有LESO 对系统的状态进行实时估计补偿。如图10 所示，扩张状态的估计值接近观测值，表示线性自抗扰控制器对包含扰动在内的扩张状态进行了有效的估计，使系统的抗干扰能力更强。仿真结果表明，LADRC 系统比PID 系统有更强的鲁棒性。

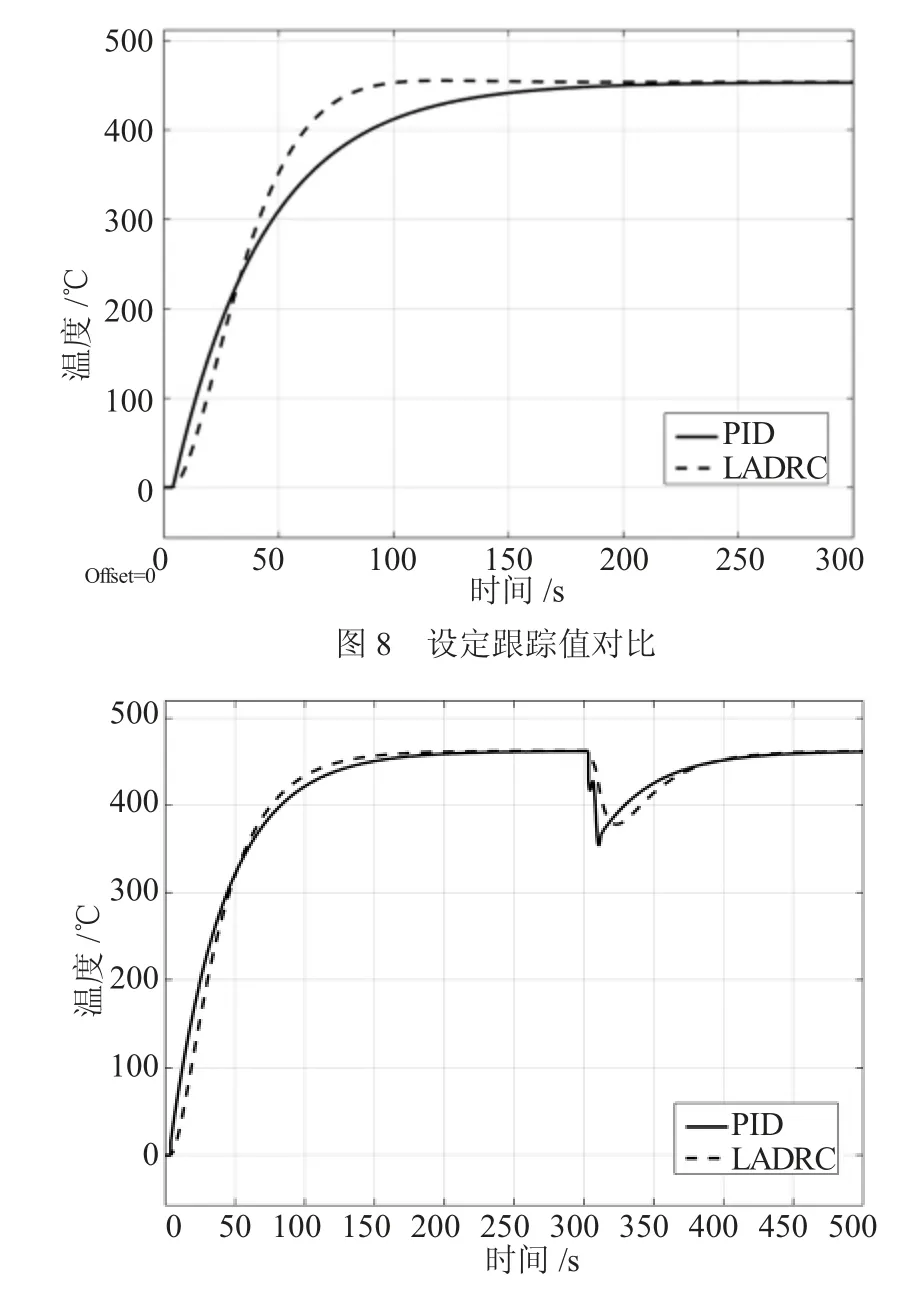
图9 抗干扰能力分析

图10 扩张状态曲线

6 结论

通过对实验平台的数据采集，利用MATLAB进行系统辨识，得到了真空感应炉的一阶时滞模型。对于模型中出现的时滞性、不确定性，提出了真空感应炉的线性自抗扰控制。同时用双轨迹法确定了稳定域边界，并用劳斯判据确定了系统的稳定性。在SIMULINK 仿真实验中，分别进行了设定值跟踪实验，以及抗干扰实验。实验结果表明:LDARC 比PID 控制抗干扰能力更强，鲁棒性更强。由于LADRC 中的扩张状态观测器能对系统的状态以及扰动等不确定因素进行实时估计并补偿；并且LADRC 中需要整定的参数只有ωc，这使LADRC 更利于实际的工程应用。