基于ORB算法和改进KNN-RANSAC算法的无人机遥感影像拼接

朱军桃,龚朝飞,赵苗兴,王 雷,冯立朋

(1.桂林理工大学 a.测绘地理信息学院;b.广西空间信息与测绘重点实验室,广西 桂林 541006; 2.南方测绘科技股份有限公司,广州 510700)

无人机遥感是一种新型的遥感技术手段,具有机动性高、作业速度快、成本低及分辨率高等优势。 无人机遥感影像的拼接技术广泛应用于航海、军事、农业等领域,其功能是将若干张遥感影像通过提取、匹配、拼接等过程生成一幅视野宽广的场景影像[1]。 常见的拼接算法有变换域法、灰度法、特征点法。 特征点法对光照条件、旋转等变化呈现出良好的鲁棒性,具有更高的可靠性,所以是目前影像拼接的主流方向[2]。 特征点提取算法主要有ORB算法[3-4]、SIFT算法[5]、SURF[6]算法等。

本文先用ORB算法提取特征点， 再运用改进的KNN-RANSAC算法进行特征匹配,该方法主要通过三方面来改进: 一是以块为单位进行匹配点的选取; 二是快速删除不合理的单应性矩阵,减少内点的检测时间; 三是通过最小化代价函数迭代优化单应性矩阵， 最后用改进的加权平均算法对图像进行融合从而完成影像的无缝拼接,得到全景影像。

1 ORB算法

ORB特征点检测算法是Rublee等[7]于2011年在ICCV上提出的,该特征点检测算法是基于FAST算法和BRIEF算法提出的一种新算法，可应用于特征点的提取,其提取效率其计算速度比 SIFT 快两个数量级，匹配性能也不比SURF逊色。

1.1 FAST算法

FAST检测算法由Rosten等[8]提出,该算法只是一种特征点检测算法,无法实现特征描述处理。FAST算法进行特征点检测的主要步骤如下[9-10]:假定点q是图像I中的一个像素点,该点的像素值记为Iq,同时设置一个像素强度阈值T，如果在圆中存在n个连续的像素,这些像素比候选像素Iq的强度加上阈值T更亮(图1)；或者比Iq减去阈值T要暗,则认为q是一个角点(特征点)。

图1 FAST角点检测Fig.1 Corner detection of FAST algorithm

FAST检测算法由于高效的检测效率而被广泛使用，但是FAST算法检测出来的特征点没有方向。这时引进强度质心算法,其基本思想是: 假设某个角点的强度偏离其质心,把这个偏离的距离用一个向量表示为

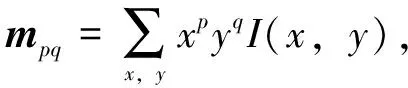
(1)

式中：(x，y)为图像中的像素点的坐标，I(x，y)为该点的强度值，强度质心可表示为

C=(m10/m00,m01/m00),

(2)

式中:m10/m00为X轴方向的质心;m01/m00为Y轴方向的质心。 这样可以把从特征点O到强度质心C两点之间的距离组成一个向量OC,该向量的方向便可作为FAST特征点的方向:

α=arctan 2(m01/m10),

(3)

即得到FAST检测算法oFAST。

1.2 BRIEF算法

BRIEF算法是一种基于二进制字符串的描述符,计算起来简单快捷。它先将图像进行平滑处理,然后测试并创建位向量[11-12]。

在一块大小为S×S的像素块上，运用ORB算法选定一个图像片段p，定义一个二进制检测τ

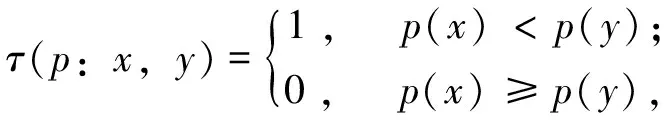
(4)

式中:x、y是图像片段p中的任意两个像素点；p(x)、p(y)是经过平滑处理的图像片段p在点(x，y)处的灰度强度值。在图像片段p中选择n个点对(x，y)，用BRIEF特征描述符定义一个包含nd维的二进制测试集

(5)

在BRIEF算法中,为了协调算法的运行速度、存储效率和识别率,nd值在BRIEF算法中一般取256。为了使上述算法生成的特征描述符具有旋转不变性,通过FAST特征点检测的特征点的方向确定BRIEF特征描述符的方向,并将其记为rBRIEF[13]:对于任何在点(xi,yi)处的特征集,其n维二进制测试后得到一个2×n维的矩阵

(6)

记由1.1节角点方向α=arctan 2(m01/m10)得到作为旋转矩阵Rα

(7)

Sα=Rα·S。

(8)

最终得到了改进的BRIEF特征描述符rBRIEF

gn(p,α):=fn(p)|(xi,yi)∈Sα。

(9)

综上,ORB算法是将有方向的FAST检测算法oFAST和rBRIEF特征描述符结合而成的一种新的特征点检测算法。

2 特征点的匹配

2.1 基于KNN(K-Nearest-Neighbor)算法的粗匹配

KNN算法又叫K最近邻算法，是进行数据分类的一种较为简单的算法,该算法的核心思想是倘若一个样本在特征空间K个最相邻的样本中的大多数样本都属于某一个类别,那么该样本也将同样属于该类别。 简单来讲，该算法的分类原则为少数服从多数的原则。

从图2可知,有两个不同类型的样本数据： 一类样本是正方形,另一类样本是三角形。 位于中心的圆形即是待分类的数据。 当K=3时,样本空间位于实线圆内,此时离圆点最近的是2个三角形和1个正方形,由于三角形数量多于正方形,此时将该圆点归到三角形一类; 当K=5时,样本空间延伸到虚线圆内,离圆点最近的有3个正方形和2个三角形,此时正方形占多数,故此时将圆形划分到正方形一类数据中[14]。

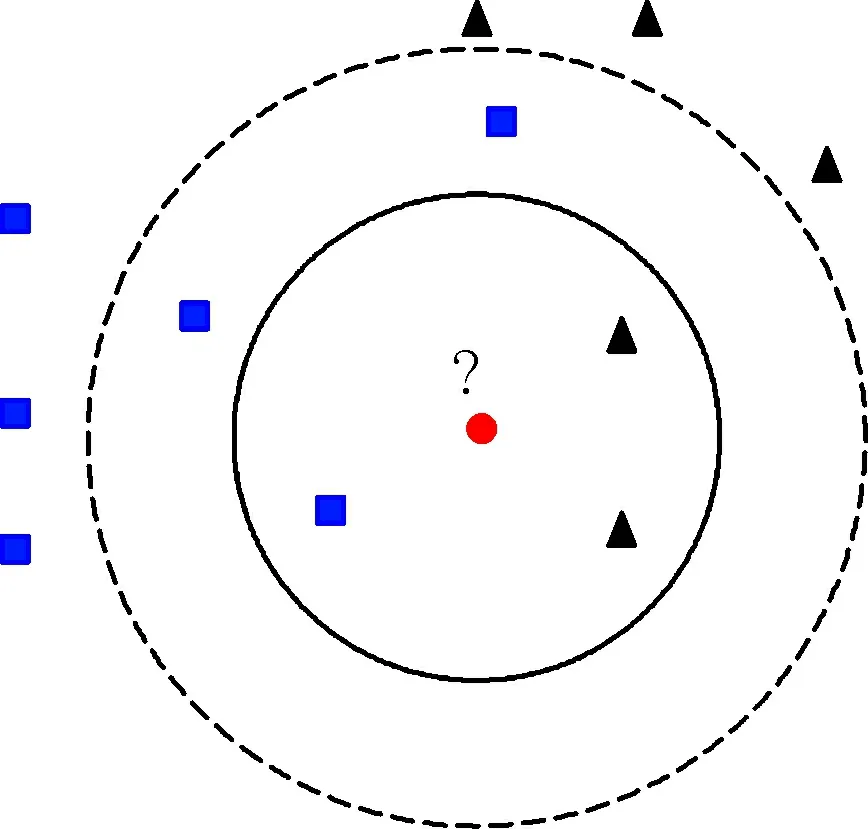
图2 KNN算法简化图Fig.2 Simplified sketch of KNN algorithm

为了提升KNN算法的匹配速度,一般都会选用合适的搜索方法。 常用的搜索算法有KD树搜索算法和LSH算法。 其中KD树搜索算法主要应用于高维空间关键数据的搜索处理[15-16],而LSH算法是为了解决局部敏感问题。 本文选用KD树搜索算法用于影像的粗匹配。

2.2 改进的RANSAC算法

2.2.1 以块为单位进行匹配点的选取 随机选择4块,再从每块中随机选择1个点，这样的选取方式可以消除因点之间的距离太近而对参数精度产生的影响[17]。具体地，先计算出待配准图像中匹配点坐标的最大值和最小值,然后将待配准图像中包含匹配点的区域平均分成3×3块,如图3所示。为了处理好匹配点的选择不公平问题,采用随机块的选取,选取方法如图4所示。

图3 匹配点分块示意图Fig.3 Schematic diagram block diagram of matching points

图4 随机块选取方法示意图Fig.4 Schetch of random block selection method

假设目标图像一共被分为M块,那么区间[0,1]被分成M个间隔,每个间隔的宽度d为

(10)

式中:ni为第i块的匹配点数目。 在实际问题中进行块的随机提取时,如果生成一个[0,1] 均匀分布随机数并落在第i个区间上,那么第i块即被选中。

2.2.2 快速删除不合理的单应性矩阵 在估计出初始单应矩阵之后,随机从剩余匹配点对中选取一对匹配点,检验这对匹配点是否适合该单应性矩阵:如果适合,则继续执行下一步操作;否则,剔除该单应矩阵,重新选取匹配点对进行估计，以减少内点的检测时间。

2.2.3 利用L-M非线性优化方法算法 针对内点集中的匹配点对Mi(x,y)和Ni(x′,y′),点Ni(x′,y′)通过单应性矩阵H投影变换后得到的点的坐标记为Ni′(u,v)，那么投影变换前后的误差指标函数为

(11)

式中:ei表示当前误差,n表示内点的数量。

假定Hk为第k次迭代求出的单应性矩阵,更新后的单应性矩阵为

Hk+1=Hk+ΔH,

(12)

ΔH=[JT(H)J(H)+λI]-1JT(H)e(H)，

(13)

式中:e(H)表示误差指标函数中的ei(H)；I表示单位矩阵；J(H)为雅可比矩阵； 参数λ(λ>0)是一个比例系数(当λ较大时,L-M算法近似于梯度下降算法；当λ较小时,L-M算法近似于高斯牛顿算法)。 每迭代成功一步,参数λ就会相应地减小,当误差指标函数与最小值接近时,此时的算法计算速度也最快,同时该时刻的单应性矩阵的精度也最高。

2.2.4 改进后的 RANSAC算法 ①从初始匹配点对集合U中,按照图3、图4的分块方法及公式随机选取4个点对作为一个内点集合，并将其记为Ui; ②用线性方程组的方法解算出初始单应性矩阵Hi; ③从U-Ui中随机地选取1对匹配点,若该点对能够通过单应性矩阵Hi(投影误差小于给定的阈值)检验,则将该点对加入集合Ui中,否则舍弃单应性矩阵Hi,返回到步骤②重新选择样本进行初始单应矩阵的估计; ④使用单应性矩阵Hi去检验集合U-Ui中所有的匹配点对,如果某个点对的投影误差小于给定的阈值,便可将其加入集合Ui中去; ⑤若集合Ui中的内点数量小于阈值T,那么返回到步骤③重新选择样本进行初始单应矩阵的估计,否则利用Ui对单应性矩阵Hi进行重新估计,并且通过投影误差来对单应性矩阵Hi进行评估; ⑥如此迭代反复步骤②～⑤k次,最终找出最优单应矩阵Hi及与之相对应的集合Ui,并使用集合Ui估计单应矩阵H; ⑦通过单应性矩阵H计算出集合Ui中每个点对的投影误差ei(H)以及误差指标函数E(H); ⑧计算单应性矩阵H各分量相对于ei(H)的偏导数与J(H),从而求得H的增量ΔH; ⑨如果E(Hk)小于给定的阈值,则可终止运算,此时得到单应性矩阵H即为迭代优化后的最优单应性矩阵H; ⑩如果E(Hk+1)小于E(Hk),但是大于给定的阈值,则减小参数λ的值,返回到步骤⑧； 否则， 使参数λ的值变大,返回到步骤⑨。

3 实验与结果分析

3.1 特征点检测算法实验

对特征点提取算法进行具体的实验分析,图5、图6是两组遥感影像图,通过不同区域的划分来进行对比实验。在特征点提取方面,主要用SIFT算法与本文算法进行对比。以图5为例,提取结果见图7、图8。

从实验结果可以看出,SIFT提取到的特征点远多于本文算法,但是实际匹配数很接近(表1)。这说明本文所选取的ORB特征点提取算法能达到实验效果,由于ORB算法是选用的FAST快速角点检测,所需时间远低于SIFT特征点提取算法,其处理速度约是SIFT的38倍,在实用性方面也高于SIFT算法。

3.2 影像匹配结果

针对改进KNN-RANSAC算法进行影像的特征匹配实验,并与传统KNN-RANSAC算法进行对比。 以图6为例,分别进行ORB-改进的KNN-RANSAC特征匹配、SIFT-KNN-RANSAC特征匹配、ORB-KNN-RANSAC特征匹配,如图9所示。

图5 实验用图(第一组)Fig.5 Maps of experiment group 1

图6 实验用图(第二组)Fig.6 Maps of experiment group 2

图7 SIFT特征点提取结果Fig.7 Feature points extraction results of SIFT algorithm

图8 本文特征点提取结果Fig.8 Feature points extraction results of algorithm in this paper

图9 不同改进算法的KNN-RANSAC特征匹配图像Fig.9 KNN-RANSAC feature matching of different improved algorithms

表1 不同算法的性能对比Table 1 Performance comparison of different algorithms

由匹配对连线结果可以看出,不同匹配方法所完成的匹配对数差异不大。 本文采用改进的KNN-RANSAC算法滤除误匹配点之后,直接显示匹配结果,极大地降低了匹配时间且能达到更高的匹配率,详见表2。

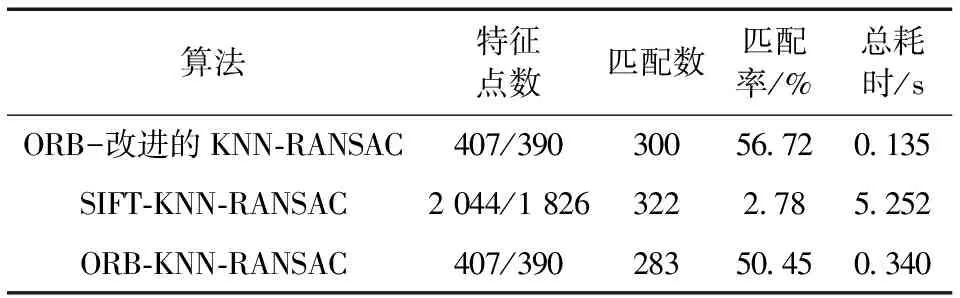
表2 不同算法的特征匹配Table 2 Feature matching of different algorithms

注: 匹配率=匹配个数2/两幅图特征点数之积。

3.3 影像融合拼接结果

对特征匹配后的影像进行融合拼接。 以图5为例得出3种特征匹配的融合结果,其中图10a—d分别为ORB-改进的KNN-RANSAC、SIFT-KNN-RANSAC、ORB-KNN-RANSAC、ORB-改进的KNN-RANSAC特征匹配改进加权融合结果图,可以看出配准后的影像直接拼接会出现重影、错位等现象。

本文采用改进加权平均算法对图像进行融合处理,实验表明该方法能有效消除重影、错位等现象,最终拼接结果如图10d、图11、图12所示。

4 结 论

本文提出的影像匹配算法,先用ORB算法提取特征点,再用改进的KNN-RANSAC算法来快速删除误匹配点以及进行特征点匹配,最后对影像进行改进加权融合。

实验结果表明，本文算法对于SIFT算法在保证精度的前提下匹配速度有很大的提高,同时改进的KNN-RANSAC算法在匹配速度上明显优于传统方法,从而证明了本文算法的优越性。

图10 图像融合对比Fig.10 Comparison of image fusion

图11 三幅影像拼接结果Fig.11 Mosaic results of three images

图12 十幅影像拼接结果Fig.12 Mosaic results of ten images