空间误差模型的变量选择

刘宣， 马海强， 邓胜伶

( 1.阳光学院 基础教研部， 福建 福州 350015； 2.江西财经大学 统计学院， 江西 南昌 330013 )

空间计量模型是一种描述地理单元间空间相依关系的模型，因其具有简单、直观和易解释等特点而被广泛应用于经济、管理、能源和交通等领域.空间计量模型的已有研究主要集中在参数估计和假设检验两个方面[1-7].近年来，随着高维数据的出现，空间计量模型的变量选择问题引起了学者们的关注，例如：文献[8]采用自适应LASSO (least absolute shrinkage and selection operator)方法对空间自回归模型的变量选择问题进行了研究，文献[9-10]探讨了空间自回归模型变量选择的大样本渐进性质.受以上文献的启发，本文采用SCAD (smoothly clipped absolute deviation)惩罚方法对空间误差模型的变量选择问题进行研究，拟获得该问题的惩罚估计量的理论性质.

1 模型及假设

考虑空间误差模型

Yn=Xnβ+Un,Un=ρWnUn+Vn.

(1)

其中：Yn是n维向量；Xn是n×k阶设计矩阵；β是k维的回归系数；ρ是空间自相关系数，满足|ρ|<1；Wn是n阶空间权重矩阵；Vn是独立同分布的n维误差向量.

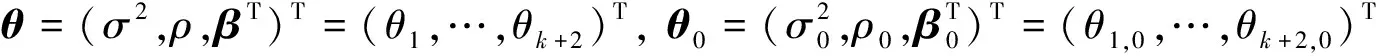
为证明估计量的大样本性质，本文给出以下正则条件：

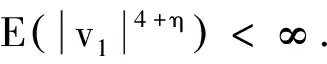
条件2 对任意的n，Xn的元素一致有界.

条件3Wn的主对角元素为0， 每一行(列)元素的绝对值之和一致有界.

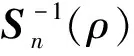
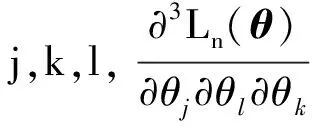
2 变量选择的方法及其证明

2.1 惩罚方法

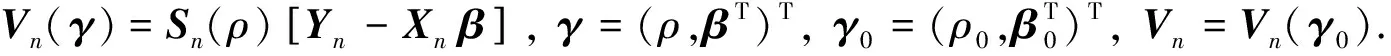
(2)

其中Ln(θ)表示拟似然函数.基于SCAD惩罚函数在经典线性模型下的优良表现[11]，本文采用惩罚对数拟似然函数的方法选择变量，并构造如下损失函数：

(3)

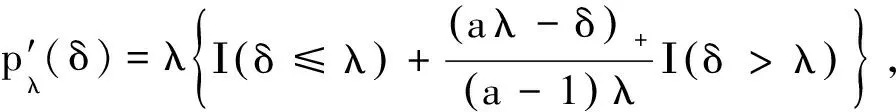
注1将式(3)所得的估计称为惩罚对数拟似然估计.为方便起见，后续简称其为惩罚似然估计.

注2由于损失函数(3)为非凸函数，因此需采用数值迭代的算法对其优化.具体迭代过程为：首先给出空间回归系数ρ的初始值(如极大似然估计值)；然后将模型(1)转换成线性模型，再采用LQA算法得到回归系数β的惩罚估计值；最后把所得估计值代入损失函数将其转化成一元函数的优化问题，并以此获得ρ的惩罚估计值.按上述方法迭代循环到相邻两次估计值的绝对偏差小于给定的精度为止，所得结果即为所求估计值.迭代过程中，调节参数λn的选择采用普通BIC准则.

2.2 大样本性质

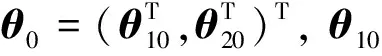
引理1若满足条件1—条件6，则有

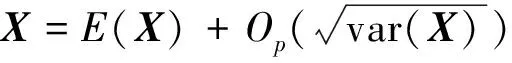
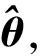
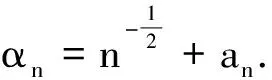
(4)

成立即可.由于pλn(0)=0， 所以

Dn(u)=Qn(θ0+αnu)-Qn(θ0)=

上述不等式右边按泰勒公式展开，有

再由引理1及相关假设条件，可得

由以上可知，存在足够大的常数C使A1和A3的值不超过A2的值，由此可推出结论(4)成立，证毕.

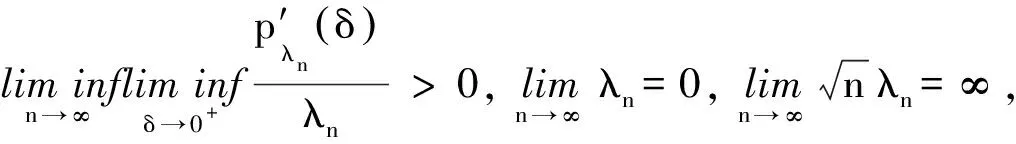
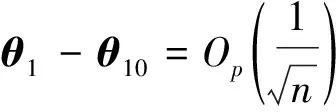
其中θ*位于θ和θ0之间.根据引理1及条件6，对j=s+1,…,d, 有

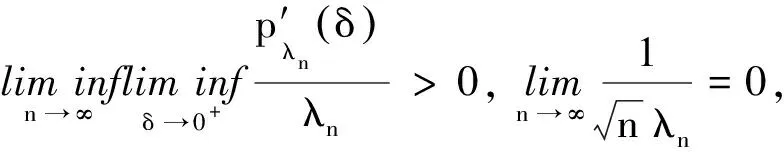
为方便描述以下定理，令：

Σ=diag{0,p″λn(|θ2,0|),p″λn(|θ3,0|),…,p″λn(|θs,0|)}，

b={0,p′λn(|θ2,0|)sgn(θ2,0),p′λn(|θ3,0|)sgn(θ3,0),…,p′λn(|θs,0|)sgn(θs,0)}.

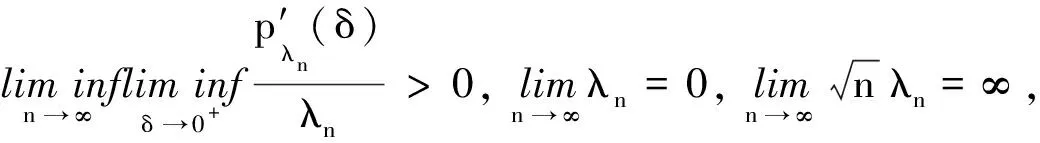
证明由定理2知(i)成立.下面证(ii).对j=2,…,s, 有

根据取得极值的必要条件，有

进而可得

(5)

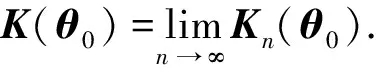
从定理1—定理3可知，由最小化损失函数(3)不仅可以得到未知参数的相合估计，还可以把零系数压缩为零从而可去掉不显著的相应变量，实现变量选择.

3 蒙特卡洛模拟

数据基于模型(1)产生.其中：协变量Xn来自满足均值为0、协方差阵为(0.5|i -j|)8×8的8维正态分布； 回归系数β取{3,2,0,0,0,1,0,0}; 空间自回归系数ρ取{0,0.3,0.7}; 空间权重矩阵为rook矩阵(边相邻的单元设为1， 否则设为0);Vn～N(0,σ2In)，σ=1,2.

用C表示100次模拟估计中零系数出现的平均数，用I表示100次模拟估计中非零系数出现的平均数，用误差平方和的中位数(MSE)反映估计的精度，惩罚函数中的调节参数a=3.7，λ的选取采用BIC准则.用“Spatial error model”表示本文方法空间误差模型下模拟的结果，“Linear model”表示忽视空间效应直接利用传统SCAD惩罚方法所产生的结果.

由表1和表2中的C值和I值可看出，随着样本量的增加，零系数的正确识别率越来越高，非零系数的错误识别率迅速降为0.该结果和惩罚估计量的理论性质一致.由表1和表2中的MSE值可以看出，惩罚估计量随样本量的增加其精度得到显著改善.由表1和表2中的“Linear model”栏可以看出，若忽略原本存在的空间效应而直接使用线性模型下相应的变量选择方法会大幅增加误差，因此空间效应不可忽视.

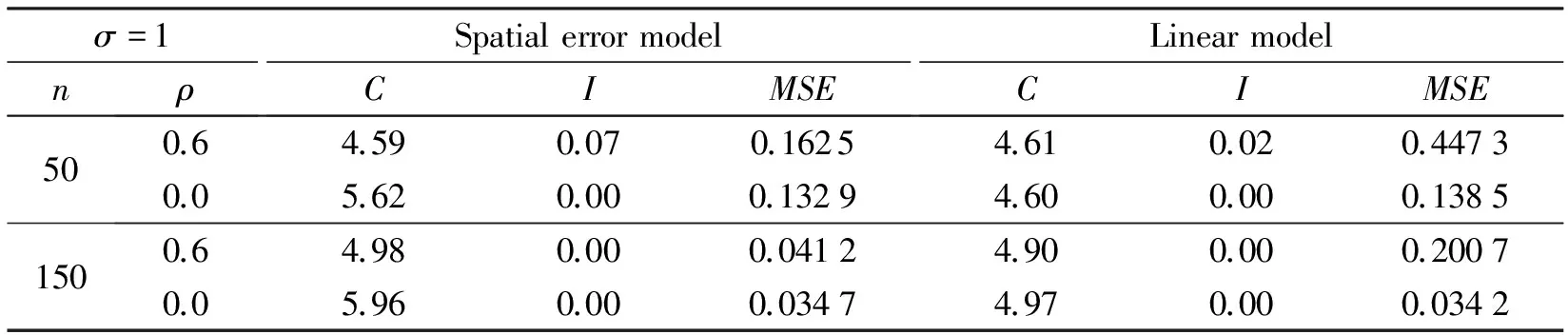
表1 σ =1时变量选择的模拟结果

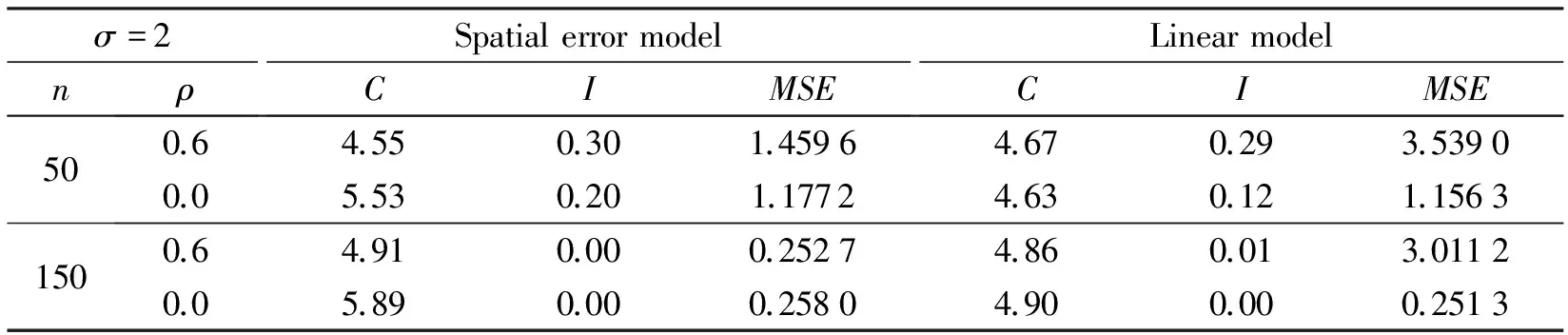
表2 σ =2时变量选择的模拟结果