基于联系数广义有序加权平均算子的三角模糊数多属性决策方法
袁宏俊, 卢敏欣, 江立辉
( 1.安徽财经大学 统计与应用数学学院, 安徽 蚌埠 233030;2.东北财经大学 统计学院, 辽宁 大连 116025; 3.安徽财经大学 金融学院, 安徽 蚌埠 233030;4.合肥学院 人工智能与大数据学院, 安徽 合肥 230601 )
0 引言
多属性决策是指决策者根据已知方案的多个不同属性值(决策信息),然后运用一定的决策方法对所得的决策信息进行评价和择优.多属性决策问题普遍存在于社会生活的诸多领域,但由于实际问题的复杂化和人们认识事物的局限性,在实际决策过程中往往出现具有模糊现象的评价问题,因此有必要开展模糊信息的多属性决策方法的研究.目前,国内外学者对三角模糊数多属性决策问题进行了广泛研究,并取得了许多研究成果[1-15].例如:徐泽水[3]针对决策者的方案偏好和属性权重信息不完全的情况,提出了一种基于相似度的三角模糊数型多属性决策方法.樊治平等[4]提出了一个确定三角模糊数多指标信息的最优划分和最优聚类中心的定理,并给出了三角模糊数信息的FCM聚类算法.黄智力等[5]针对属性权重未知的三角模糊数,利用合作博弈中的极大极小算法提出了一种基于比较可能度关系的三角模糊数多属性决策方法.卫贵武等[6]针对决策者的方案偏好和属性权重信息不完全的情况,提出了一种基于灰色关联分析GRA的三角模糊数多属性决策方法.刘秀梅等[7]针对属性值和属性权重都是三角模糊数的情况,提出了一种基于联系数的三角模糊数多属性决策方法.和媛媛等[8]在三角模糊数多属性决策中,讨论了不同三角模糊数距离测度对模糊TOPSIS决策结果的影响.胡凌云等[9]针对属性值和属性权重都是三角模糊数的情况,依据传统的TOPSIS思想提出了一种基于联系数距离的三角模糊数多属性决策方法.陈雪等[10]针对属性权重未知的三角模糊数,利用合作博弈中的可能度最大化算法提出了一种基于相对相似度关系的三角模糊数多属性决策方法.江文奇[11]针对属性值和属性权重都是三角模糊数的情况,提出了一种基于三角模糊数型VIKOR(FVIKOR)的多属性决策方法.刘秀梅等[12]针对属性权重完全未知的情况,用“均值+偏差”将三角模糊数属性值转换成联系数属性值,然后利用联系数中i的不同取值和概率统计原理来确定三角模糊数的多属性决策.刘红彬等[13]提出了一种三角模糊数Tr -PA算子和三角模糊数Tr -POWA算子,并将它们应用于三角模糊数的多属性群决策问题中.张市芳[14]依据传统的TOPSIS思想,提出了一种基于斜投影技术的三角模糊多属性决策方法.林友谅等[15]利用多种决策方法进行信息集结,提出了一种基于有序加权平均(OWA)算子的三角模糊数多属性组合决策方法.受上述文献的启发,本文针对属性值和属性权重都是三角模糊数的多属性决策问题,采用等价转换的思想将属性值和属性权重的三角模糊数转换成二元联系数;在有序加权平均算子的基础上,利用广义平均数的方法将二元联系数作为信息集成的数据对象,构建一种新型的联系数广义有序加权平均(CNGOWA)算子,并提出一种基于CNGOWA算子的三角模糊数多属性决策方法.
1 三角模糊数和联系数的基本概念
定义1[3]若实数满足aL≤aM≤aU, 称Y=[aL,aM,aU]为三角模糊数,其中aL是三角模糊数的下界,aU是三角模糊数的上界,aM是三角模糊数的中值(即内部最大可能性的数).三角模糊数的隶属函数可表示为
当aL≥0, 称Y=[aL,aM,aU]为非负三角模糊数;当三角模糊数的下界aL、上界aU和中值aM满足aM-aL=aU-aM时,称Y=[aL,aM,aU]为对称三角模糊数;当aL=aM=aU时,三角模糊数退化为普通实数.

2 三角模糊数转换成联系数
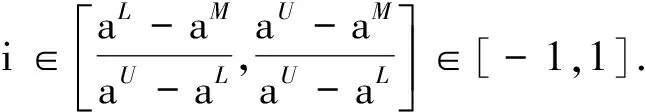
利用定义3即可将三角模糊数的多属性决策问题转化成二元联系数的多属性决策问题.
3 联系数的运算规则和联系数的比较
定义4设二元联系数u1=a1+b1i,u2=a2+b2i, 其中i∈[-1,1], 并定义相应的运算为:
1)u1⊕u2=(a1+a2)+(b1+b2)i;
2)u1⊗u2=a1a2+(a1b2+a2b1+b1b2)i;
3)ku1=(ka1)+(kb1)i;
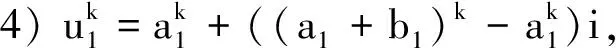
根据定义4,二元联系数可以很便利地进行相关运算.此外,运用以下定义5和定义6还可以从“均值-方差”的角度度量不同二元联系数的大小,并比较大小和排序.
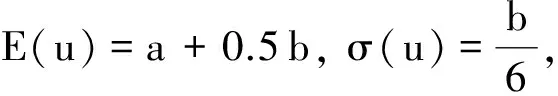
定义6[17]设二元联系数u1=a1+b1i,u2=a2+b2i,a1,a2,b1,b2∈R+, 若:
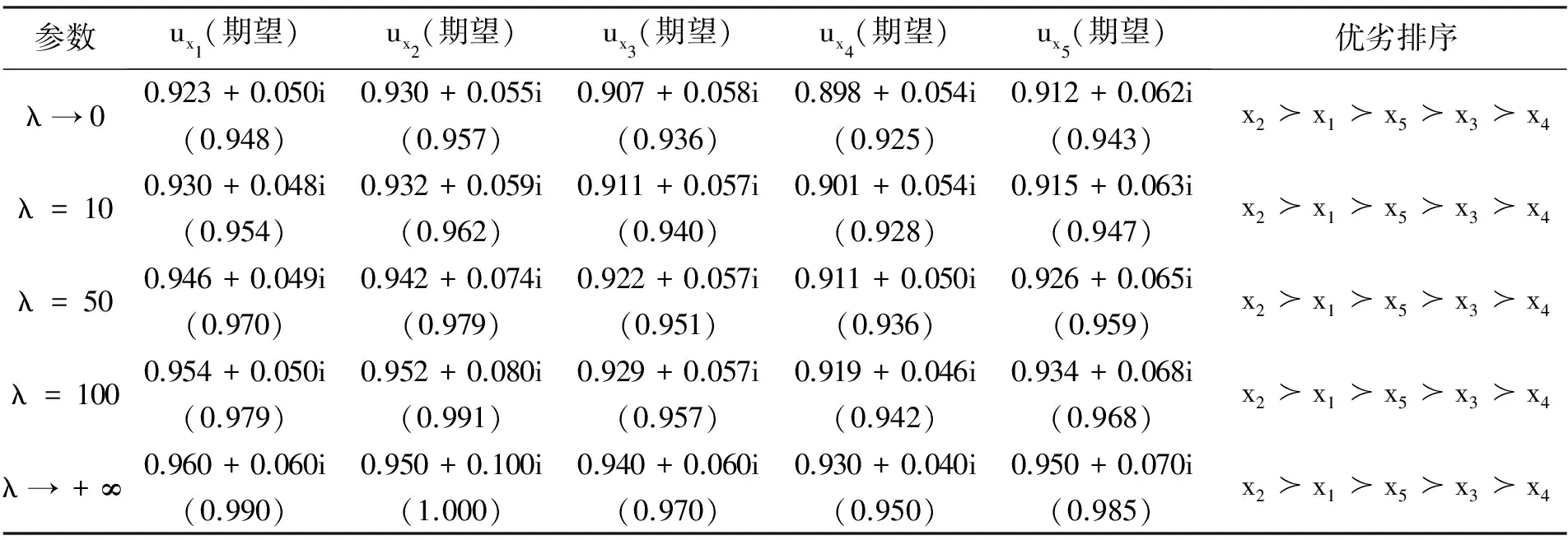
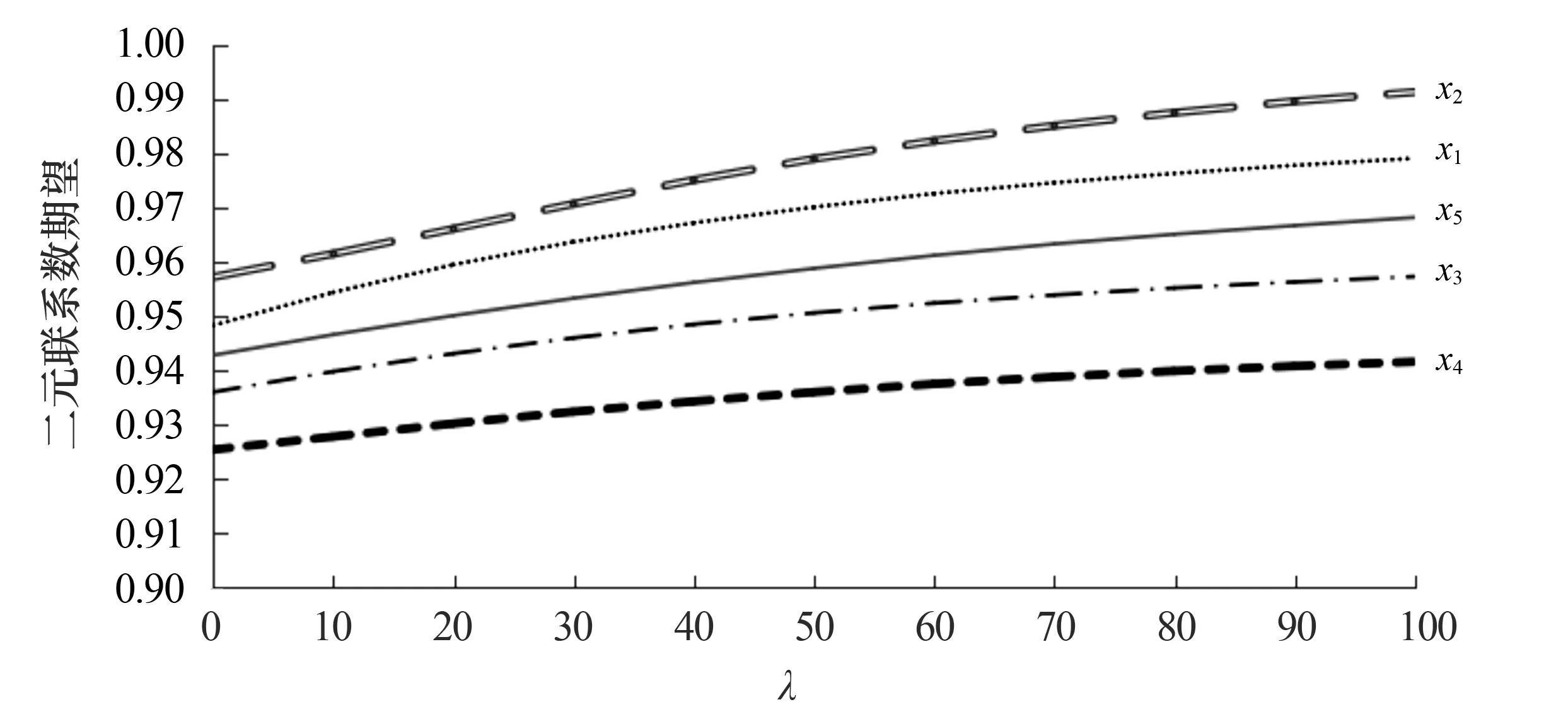
1)E(u1) 2)E(u1)=E(u2), 则有: ①当σ(u1)<σ(u2)时,u1 在定义7中,当参数λ取不同数值时,可以得到以下不同的联系数信息集成算子: ① 当λ=1时,CNGOWA算子即为联系数有序加权算术平均(CNOWA)算子: CNOWA(u1,u2,…,un)=(w1v1)⊕(w2v2)⊕…⊕(wnvn); ②当λ→0时,CNGOWA算子即为联系数有序加权几何平均(CNOWGA)算子: ③当λ→ +∞时,CNGOWA算子即为联系数有序最大化(CNOM)算子: CNOM(u1,u2,…,un)=max{u1,u2,…,un}=v1. CNGOWA算子满足下列性质: 性质2(幂等性) 若二元联系数数组u1,u2,…,un满足ui=u,∀i=1,2,…,n, 则有CNGOWA(u1,u2,…,un)=u. 性质3(有界性) 若u1,u2,…,un是二元联系数数组,则有min{u1,u2,…,un}≤CNGOWA(u1,u2,…,un)≤max{u1,u2,…,un}. 性质4(置换不变性) 若二元联系数数组u′1,u′2,…,u′n是u1,u2,…,un的任意一个置换,则有CNGOWA(u′1,u′2,…,u′n)=CNGOWA(u1,u2,…,un). 步骤3 利用CNGOWA算子集成二元联系数属性值的信息.利用定义7中的CNGOWA算子,将二元联系数属性值us k(us k=as k+bs ki)和实数权重wk进行信息集成,由此得出每一种方案的CNGOWA算子的综合二元联系数决策值us,us=as+bsi,s=1,2,…,m. 步骤4 确定方案的优劣排序和最优方案.利用定义6的二元联系数期望和二元联系数方差,对CNGOWA算子的综合二元联系数决策值us的大小进行判定,并给出其对应方案的优劣排序.如果原属性值是效益型指标,则CNGOWA算子的综合二元联系数决策值中的最大值所对应的方案是最优的;如果原属性值是成本型指标,则CNGOWA算子的综合二元联系数决策值中的最小值所对应的方案是最优的. 为了验证文中提出的基于CNGOWA算子的三角模糊数多属性决策方法的有效性和可行性,采用文献[5,7,10]中的实例数据进行验证. 实例1某单位考核选拔干部时,选取思想品德d1、 工作态度d2、 工作作风d3、 文化水平d4、 领导能力d5、 开拓能力d6等6个属性作为评价指标.各指标对应的属性权重为三角模糊数数据,分别为W1= [0.10, 0.15, 0.20],W2=[0.05, 0.10, 0.15],W3=[0.20, 0.25, 0.30],W4=[0.05, 0.10, 0.15],W5= [0.15, 0.20, 0.25],W6=[0.10, 0.15, 0.20].现有5名候选人x1,x2,x3,x4,x5参加竞选,由群众推荐评议.评议按照所给的属性评价指标打分,候选人在某属性指标上获得的分值越大,表明候选人在该属性指标上越优秀.由于群众对每个候选人的属性评价指标打分不同,因此需对分数进行统计处理后再用三角模糊数数据表示属性评价指标值,结果见表1.根据表1试确定所有候选人的优劣排序和最优候选人. 表1 5位候选人的属性评价值(三角模糊数的数据形式) 步骤1 利用定义3, 将表1中5位候选人的三角模糊数属性评价值转换成二元联系数属性评价值,结果见表2. 表2 5位候选人的属性评价值(二元联系数的数据形式) 步骤2 将三角模糊数属性权重转换成CNGOWA算子中的实数权重.首先将三角模糊数属性权重转换成二元联系数属性权重,分别为: W′1=0.15+0.10i,W′2=0.10+0.10i,W′3=0.25+0.10i, W′4=0.10+0.10i,W′5=0.20+0.10i,W′6=0.15+0.10i. 然后利用定义5计算出二元联系数属性权重的期望,分别为: E(W′1)=0.20,E(W′2)=0.15,E(W′3)=0.30,E(W′4)=0.15,E(W′5)=0.25,E(W′6)=0.20. w1=0.16,w2=0.12,w3=0.24,w4=0.12,w5=0.20,w6=0.16. 步骤3 利用CNGOWA算子对二元联系数属性值的信息进行集成.将步骤1中的二元联系数属性值和步骤2中的实数权重代入定义7中的CNGOWA算子表达式,可得到每一个候选人的CNGOWA算子的综合二元联系数决策值: 步骤4 确定5名候选人的优劣排序和最优候选人.在上述CNGOWA算子的综合二元联系数决策值中,参数λ(λ∈(0,+∞))有无穷多种取值,但为了计算简便随机选取5种代表性参数(λ→0,λ=10,λ=50,λ=100,λ→ +∞), 并分别计算5位候选人在每种具体参数下的综合二元联系数决策值.由于原三角模糊数属性值都是数值越大越好的效益型指标,因此可根据定义5和定义6对5名候选人的综合二元联系数决策值的大小进行判定.判定时按照数值越大候选人排序越靠前的原则进行优劣排序,其中综合二元联系数决策值最大的候选人就是最优候选人.5种参数下5名候选人的综合二元联系数决策值和优劣排序见表3. 表3 5名候选人的综合二元联系数决策值及其优劣排序 由表3可知,5种参数下5位候选人的综合二元联系数决策值的优劣排序均为x2,x1,x5,x3,x4, 由此可以判定x2是最优候选人.该排序结果与文献[5]、文献[7]和文献[10]中的结果一致. 在实例分析中,本文仅选取了5个代表性参数对5位候选人的综合二元联系数决策值进行了优劣排序的研究.为验证本文方法在取其他参数时的灵敏度和稳定性,本文在参数λ∈(0,100]范围内对5位候选人的综合二元联系数决策值以及生成的优劣排序结果进行了考察,结果如图1所示.由图1可以看出,5位候选人的综合二元联系数决策值期望在λ∈(0,100]内都是单调递增曲线,且各曲线的上下位置关系未发生改变.另外,在同一参数下5位候选人的综合二元联系数期望值都是候选人x2最大,其次依次为x1,x5,x3,x4.该结果与实例分析所得结果一致,表明本文方法稳定、可靠. 图1 5位候选人的综合二元联系数的期望变化 研究表明,本文提出的基于CNGOWA算子的三角模糊数多属性决策方法计算简单,在参数λ∈(0,100]范围内稳定性好,且5位候选人的排序结果与文献[5]、文献[7]和文献[10]中的方法结果一致,表明本文提出的方法是一种合理有效的三角模糊数的多属性决策方法.研究中,本文只针对三角模糊数的模糊数据进行了分析,今后我们将探讨CNGOWA算子应用于其他模糊数据中的情形,如区间数、梯形模糊数、直觉模糊数、语言变量等,以此构建基于CNGOWA算子的模糊数据的多属性决策方法.4 联系数广义有序加权平均(CNGOWA)算子的概念及其性质

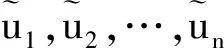
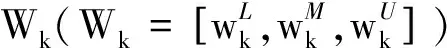
5 基于CNGOWA算子的三角模糊数多属性决策方法
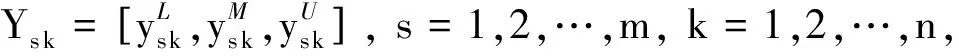
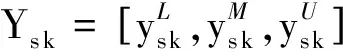
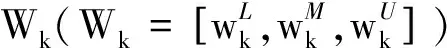
6 实例分析


7 方法的灵敏度和稳定性分析
8 结论

