基于改进的全变分图像去噪算法研究
谈晶圩,杨 敏
(南京邮电大学 自动化学院、人工智能学院,江苏 南京 210023)
图像去噪[1]是图像处理中的基本问题,其中全变分正则化模型[2]是应用最普遍的去噪模型,能很好地保护图像边缘信息,但容易产生梯阶效应。研究者在模型和数值计算上对全变分模型进行改进,如广义全变分[3]、交叠组稀疏全变分[4]、分数阶全变分[5]等,这些方法在定义梯度时只局限于垂直和水平方向,忽略了图像许多结构特征,在图像复原时纹理结构容易丢失,Chambolle等[6]在有限差分基础上提出了迎风有限差分,从更多方向上定义梯度。
本文针对全变分模型梯阶效应明显的问题,受文献[7]的启发,在经典的全变分去噪模型的基础上,将迎风差分引入全变分正则项中,将迎风全变分代替传统全变分去噪模型中的各向异性全变分部分,利用迎风有限差分定义梯度,更充分地考虑邻域梯度信息,从而改善去噪性能,减少伪影,提高提取边缘能力。在模型计算时采用原偶混合梯度算法[8]迭代优化求解,基于对偶理论,将全变分模型转化为对偶求解,既改善了去噪效果,同时保持图像边缘。
这种全变分模型在结构上与具有鞍点结构的优化模型可建立对应关系,所以采用能有效求解鞍点问题的原偶混合梯度算法来求解新模型,这种数值求解算法收敛速度快,效果好。应用对偶理论将原问题转成鞍点问题来求解,分开求解原始变量和对偶变量,每步的计算量较其他算法较少,降低了计算难度。本文算法与一些优化求解算法,如拉格朗日乘子法[9]、投影法[10]、Bregman分裂迭代算法[11]和交替近端梯度法(APGM)[12]等相比,结构较为简单。因为这些优化算法均需做梯度的复合运算,而本文采用的基于预解式的原始对偶算法只需做单一的梯度运算,迭代复杂度较低。虽然ADM[13]方法是求解全变分图像复原的有效算法,一般用于有约束凸优化问题。但是,对于大型数据或者求解高维最小化问题时,原偶混合梯度算法更为简单、有效。
1 全变分新定义
数字图像中,更多的使用差分来近似导数。文献[14]使用向后差分法,把图像看作二维离散函数,最简单的x和y方向梯度近似表达式如下
图像的梯度表示为
梯度的方向是图像函数u(x,y)变化最快的方向,在图像边缘处一定有较大的梯度值,相反,图像中较平滑的部分灰度值变化较小,则相应的梯度也较小。
经典的图像梯度计算方法考虑图像的每个像素在它周围邻域内的灰度变化,利用相邻边缘的一阶或二阶导数变化规律,对原始图像中像素某个邻域进行梯度计算。
通常使用全变分正则项为各向同性,其离散定义为
传统全变分去噪模型中正则项是各向异性扩散项,边缘容易出现伪影,梯阶效应明显。梯阶效应使得图像的光滑区域趋于分片常值,伪边缘的出现严重影响图像的视觉效果。
各向同性全变分是离散全变分定义的一个有缺陷的定义,它的最小化倾向于水平和垂直结构,只考虑两个方向0°和-90°的梯度信息作为正则项约束,容易产生梯阶效应。在图像复原过程中,图像边缘的倾斜结构使全变分值也变得更大。传统全变分正则项梯度方向信息选取示意图如图1所示。
基于图像各向同性全变分的旋转不变性,即经过任意旋转后,图像各向同性全变分的值不改变,使得在图像处理的过程中找不到一个特定方向使图像各向同性全变分值最小,导致图像纹理不能够有效提取。
用迎风全变分来定义更具有各向同性的全变分模型
其中,u+表示max(u,0),迎风全变分相对于各向同性是更具各向同性的,并且容易产生尖锐的倾斜边缘,有利于减少边缘伪影。相对于上述传统方法只考虑0°和90°方向,新定义的全变分将方向0°,90°,180°,-90°的梯度作为正则项约束,更充分考虑像素点的邻域梯度。在图像处理中,它能去除浅色背景下的小而暗的噪声点。既能发挥各向同性的特征,同时具有较好的图像边缘提取效果,提高图像去噪效果。迎风全变分正则项梯度方向信息选取示意图如图2所示。
2 基于原偶混合梯度算法的模型求解
2.1 全变分模型
全变分去噪模型的无约束优化形式为其中,X表示有限维向量空间,‖·‖v表示欧几里得范数,表示梯度算子,λ表示正则化参数,u表示去噪后图像,g表示观测图像。式中第一项为正则项,代表原始图像的先验信息,第二项为保真项,用于保证去噪后图像与观测图像的相似性。正则化参数用来平衡模型中正则项与保真项,当取最优值时,才能使恢复图像效果最佳。
图像去噪是一个从噪声图像中复原清晰图像的逆问题,在去噪方法中,变分方法将逆问题建模为能量泛函的优化问题。
能量泛函的梯度下降方程为
初始值设置u=g,通过梯度下降法对图像进行反复迭代计算直到得到一个最优解,从而获得复原图像u。
2.2 原偶恢复模型
图像恢复模型是求取正则化函数的极小化,作为图像复原的结果。
式(5)中变分项是凸的、不可微、非光滑的,使得求解具有一定复杂度。原始对偶算法是近几年提出的最优化算法,因其高效的迭代方式备受关注,被广泛应用于图像处理领域。首先定义参数
一般鞍点问题即原始对偶模型表示为
一般优化问题表示为
式(8)相应的对偶问题表示为
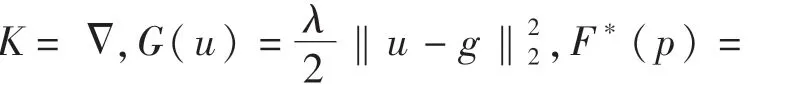
新定义的全变分图像恢复模型可与原始对偶问题建立对应关系,并采用原偶混合梯度算法进行求解。
原始模型
根据式(7),原始对偶公式为
其中,p∈Y是对偶变量,给定凸集P是对偶空间
其中,‖p‖∞表示离散无穷范数
集合P是点状球L2上的点,函数δP是集合P的指示函数,是恢复模型正则项的拓扑对偶,定义为
原始全变分问题(7)和原始对偶全变分问题(8)可以等价于对偶全变分问题
2.3 原偶混合梯度算法求解
基于预解式的原偶混合梯度算法的计算方法还需详细描述预解算子(I+∂F*)-1和(I+τ∂G)-1。
首先,令原始变量x固定,求解对偶变量y,可得y的预解式
然后,令对偶变量y固定,求解原始变量x,可得x的预解式
当函数F*和G至少有一个为凸函数时算法如下。
原偶混合梯度算法
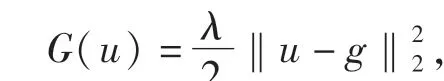
对偶变量为
3 实验结果与分析
为了验证本文算法的有效性,与相关文献算法进行比较,考虑如下具有约束的迎风差分全变分范数正则模型
测试图像如图3所示,是标准的Lena(512×512),Barara(512×512),Beth(256×256),Soccer(512×480),Dollar(512×512),Girl(768×512)图像。如图4(a)所示为加入0.3的高斯噪声的图像。
实验均在Lenovo Y7000笔记本进行,处理器为Inter(R)Core(TM)i5-8300H CPU@2.30 GHz和8 GB内存,操作系统为Windows1064位,同时仿真软件为Matlab(2018)。过去已经有证明各项同性全变分模型比各向异性模型复原效果好[15]。在本文实验中使用对比的方法如下:
(1)全变分原始对偶去噪(TV-PD);
(2)迎风全变分交替近端梯度(TVu-APGM);
(3)全变分交替近端梯度(TV-APGM);
(4)全变分Bregman(TV-Bregman)
(5)本文迎风全变分原始对偶去噪;
为了评价算法的性能,使用峰值信噪比PSNR,结构相似性SSIM 和算法迭代时间作为相应评价指标。
峰值信噪比PSNR是基于误差敏感的图像质量评价。给定一个大小m×n的干净图像I和噪声图像K,均方误差(MSE)定义为:
PSNR的值越大,失真越小。
SSIM(structural similarity)结构相似性,SSIM取值范围为[0,1],值越大,表示图像失真越小。
如表1所示,在Lena图像去噪算法对比中,迭代次数为500,4种不同的方法设置不同的参数λ,选取最优去噪效果作比较,相关对比数据见表1。
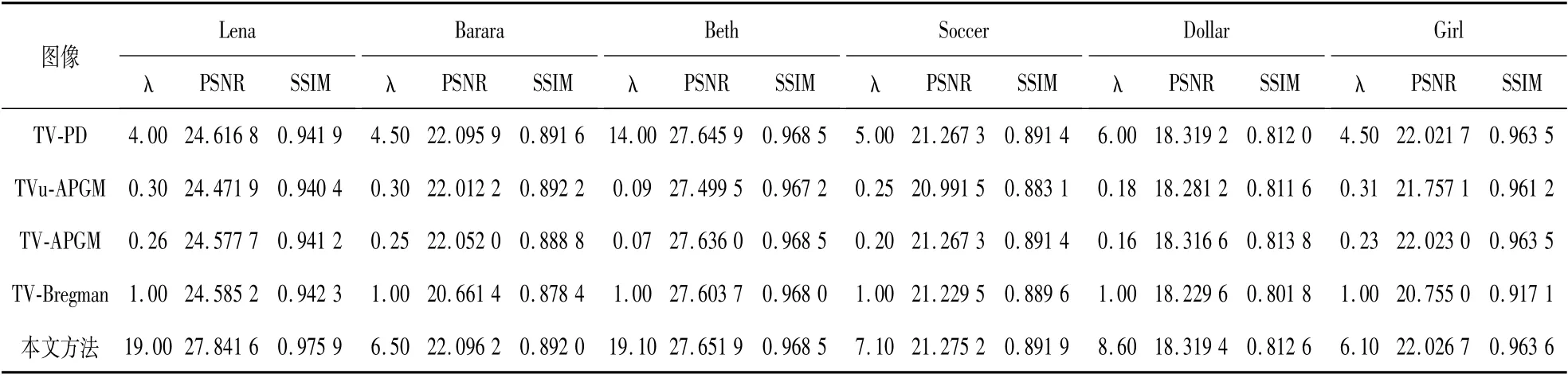
表1 图像去噪算法对比
如表1所示,4种方法的去噪效果不尽相同,本文提出的模型对图像恢复时的PSNR值均高于其他几种方法,SSIM 值也基本高于其他几种方法,说明在噪声的情况下,本文方法具有较好的去噪效果。在测试图片Lena上,初始值λ设置为19,本文方法的PSNR,SSIM在4种方法中数值最高,去噪效果和纹理信息的提取也相对较好。综上6张图片的各项评价指标的数值对比,本文方法数值效果值最优。
如表2所示,基于六张测试图像的PSNR和SSIM两个图像质量指标平均值显示,本文算法的峰值信噪比是最高的,在图像效果上有明显的提升。
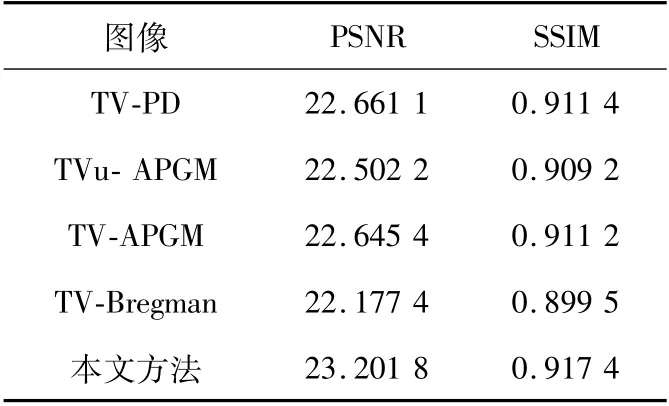
表2 各算法评价指标数值平均值对比
4 结束语
本文在全变分去噪模型基础上,对正则化项进行新定义,更多考虑边缘信息,提高了边缘结构的提取效果,并利用原偶混合梯度算法求解。相比ADM算法,子问题求解难度减小。仿真实验结果表明:在信噪比、图像一致性方面,本文方法都有所提升。但是本文算法计算时间较长,在后续的研究中,针对迭代时间过长的问题,研究如何提高优化算法的运行效率和提升图像复原效果。

