多核服务器边缘计算系统中任务卸载调度和功率分配的研究

凌雪延，王 鸿，宋荣方，2

(1.南京邮电大学 通信与信息工程学院，江苏 南京 210003 2.南京邮电大学 江苏省通信与网络技术工程研究中心，江苏 南京 210003)

近些年来，智能移动设备快速发展，交互式游戏、人脸识别、自然语言处理和3D建模等越来越多的计算密集型应用也随之出现。然而智能移动设备处理能力有限，且电池具有一定的使用寿命，如果完全在本地执行所有计算任务，必然耗时耗能，用户也无法获得良好的应用体验。为了使计算资源有限的移动设备能够运行这些计算密集型应用，同时获得良好的用户体验，移动边缘计算（Mobile Edge Computing，MEC）孕育而生［1］。在云计算中，服务器与移动用户之间的距离过于遥远，使得移动网络的核心网负载增大，同时会引发较大的网络时延。与传统云计算不同的是，MEC通过将小型的计算和存储中心，即边缘服务器，部署在靠近用户的地方，从而大幅减轻了云计算中核心网的负载和缩短了任务卸载的时延［2］。因此将计算密集型的任务从移动设备端卸载至边缘服务器可以大幅改善设备的能耗和执行时延。

MEC卸载技术常见的服务质量衡量指标有时延、能耗以及时延和能耗之间的权衡［2］，优化的方向通常要考虑移动设备和边缘服务器之间的通信和计算资源的联合分配。目前，已有大量的文献对MEC卸载技术进行了研究，从用户数量、卸载任务方式、边缘服务器处理能力三个角度，可以把这些文献分为单用户MEC系统和多用户MEC系统、完全卸载和部分卸载MEC系统、异构服务器（单核或多核）和同构服务器（单核或多核）MEC系统。在单用户单核边缘服务器MEC系统中，文献［3］对移动设备具有多个独立可卸载的计算任务的卸载调度和时延能耗的权衡问题进行了研究。基于流水车间调度模型对任务卸载调度进行建模，利用交替最小化优化方法优化系统时延能耗的加权和。文献［4］利用李雅普诺夫优化方法，对多用户多核服务器部分卸载MEC系统的时延和能耗的权衡关系进行了研究。文献［5］基于M/G/1的排队模型对单用户异构服务器部分卸载MEC系统进行建模，利用二分法搜索等一系列高效的数值方法分别对系统的平均响应时间、平均能耗和代价性能比进行了优化。

受文献［3，5］启发，同时鉴于目前对具有多核处理器的边缘服务器的MEC系统的任务卸载调度研究较少，因此本文研究的是单用户多核服务器的MEC系统。系统在用户侧具有多个独立可卸载的计算任务，在传输功率受限条件下，每个任务的传输时延和在服务器上的执行时延都是可获得的，此时系统时延与每个任务的传输时延和在服务器上的执行时延耦合在一起，若不采用合理的任务卸载顺序，必然会引起系统时延的恶化。首先，为了获得合理的任务卸载调度流程，本文基于混合流水车间调度（Hybrid Flow-shop Scheduling Problem，HFSP）模型［6］对该系统的任务卸载调度进行建模；其次，以最小化系统时延和能耗的加权和为目标，采用遗传算法对优化问题进行求解。通过仿真，获得了合理的任务卸载流程，对系统时延和卸载任务数量之间的关系以及系统能耗和系统时延之间的关系分别进行了分析。

1 系统模型和问题建模

本节首先提出了计算任务模型、系统时延模型和系统能耗模型，接着对联合任务卸载调度和功率分配的问题建模，最后最小化系统时延和能耗的加权和。

1.1 系统模型

本文研究的是单用户多核服务器的MEC系统，如图1所示该系统有一个用户和具有多核处理能力的MEC服务器，用户侧有多个独立可卸载的计算任务，并且这些任务可并行地卸载和执行。MEC服务器是运营商部署在无线接入点附近的小型数据中心，因此其可通过无线信道与移动设备连接，执行移动设备卸载的计算任务。

1.1.1 任务卸载模型

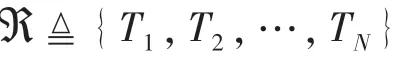
1.1.2 边缘服务器执行模型

为了将计算任务卸载到MEC服务器上执行，需要先将任务传送至MEC服务器。将N个计算任务的卸载调度决策定义为σ≜｛σ1，σ2，…，σN｝，表示这N个计算任务的卸载调度顺序，即Tσi表示该任务将于第i次卸载到MEC服务器上。其中σ应满足σi∈｛1，2，…，N｝，且σi≠σj，i≠j，∀i，j=1，2，…，N。同时，移动设备配备一根天线，一次仅能发送一个任务，对于多天线的场景将在以后的研究中进一步考虑。因此，任务Ti的传输速率如下

其中，Pi是任务Ti的传输功率，其为传输功率向量P的一个分量，g0是路径损耗常数，θ是路径损耗指数，取值范围一般为2～4［8］，L0是参考距离，L是移动设备和MEC服务器间的距离，ω是系统带宽，N0是MEC服务器接收端的噪声功率谱密度。

MEC服务器具有M核处理器，并且具有相同的处理能力，将其主频记为fser。假设每个核按照先到先服务的方式独立地完成一个任务，并且在空闲时才能处理下一个任务，则M核处理器最多可同时处理M个任务。假设MEC服务器配备有容量无限大的任务缓冲区来存储尚未执行的任务。因此每个核上任务的执行顺序，不仅和任务的卸载顺序、传输时间有关，也和任务在服务器上的执行时间有关。

1.1.3 系统时延和能耗模型

混合流水车间调度解决的问题是确定并行机器的分配情况以及同一台机器上工件的加工顺序，使得系统加工时间最小化，其模型如图2所示。n个工件在包含m个阶段的流水线上进行加工，每个工件依次通过每个阶段，每个阶段的机器数为c_m，每个阶段至少有一台加工机器并且至少有一个阶段包含多台并行机器［9］。并且模型满足以下假设：（1）同一阶段中所有机器都相同；（2）每个工件可以在某阶段的任意一台机器上进行加工；（3）任意时刻每个工件至多在一台机器上加工；（4）每台机器某时刻只能加工一个工件；（5）工件的加工过程不允许中断；（6）每一台机器都有一个无限大的空间存储等待加工的工件［9］。

在单用户多核服务器MEC系统中，可以将计算任务看成是待加工的工件，每个计算任务都需要经过本地传输和服务器执行两道工序，有序地卸载到MEC服务器上执行。工序一只有移动设备的发射机这一台机器；在工序二中，MEC服务器具有M个计算能力相同的处理器，即有M台机器。因此可以用混合流水车间调度模型对单用户多核服务器MEC系统的任务卸载调度进行建模。

给定任务卸载决策σ和传输功率向量P，当任务Tσj卸载到MEC服务器上执行时，系统时延由三部分组成，即任务上传到服务器的时间t（1，σj）、任务在服务器执行的时间t（2，σj）和任务结果反馈到移动设备的时间，通常计算任务执行结果的数据量很小，因此可忽略结果的反馈时间。

其中，式（2）和式（3）分别表示任务在第一道工序和第二道工序上的加工时间。

任务Tσj卸载到MEC服务器上执行时，首先加工第一道工序，在空闲机器上按σ特定任务顺序依次处理；接着加工第二道工序，按照先完工先加工的原则，在空闲机器上优先加工当前可用任务（已在上一道工序完成的任务），以此类推直到最后一个任务在最后一个工序完工［10］。任务完工时延的递推过程如下：

其中，ik表示第k道工序的某台机器，σj表示卸载决策中的第j个任务。式（4）表示第一个任务在第一道工序的完工时间等于其在第一道工序的加工时间；式（5）表示第j个任务在第一道工序的完工时间，等于同一机器上紧前任务第一道工序的完工时间加上任务j在第一道工序的加工时间；式（6）表示第一个任务在第k道工序的完工的时间等于该任务紧前工序的完工时间加上第一个任务在当前工序的加工时间；式（7）表示任务j在第k道工序的完工时间，等于任务j紧前工序的完工时间和同一机器紧前任务j-1的完工时间中的最大值，加上任务j在第k道工序的加工时间。所以在单用户多核服务器MEC系统中，系统时延为最后一个任务在第二道工序服务器某个核上的完工时间，即C（i2，σN），它是关于任务卸载决策σ和传输功率向量P的函数，由此获得系统时延的计算范式。

移动设备将任务卸载到服务器上执行时，系统能耗由两部分组成：任务传输到服务器的能耗Eup和任务在服务器上执行的能耗Eexe，由于MEC服务器侧有电源供给，所以系统能耗的研究重点在于Eup，

1.2 问题建模

基于以上分析，本文以最小化系统时延和能耗的加权和为目标，对联合任务卸载调度和功率分配问题的建模如下：

其中，η是一个权重因子，用于调节系统时延和能耗的权衡，当其较大时，表示对系统能耗的优化更为看重，反之则对系统时延的优化更为看重。式（10）使得任务的传输功率控制在合理的范围内。式（11）使得任务的卸载决策是有效的。

不难看出该优化问题是一个混合整数非线性规划问题，虽然理论上可以利用穷举算法对其求解，但复杂度太高不便求解。考虑到遗传算法（genetic algorithm，GA）［11］是一种通过模拟自然进化过程搜索最优解的方法，具有以下特点：（1）对结构对象进行操作，不存在求导和函数连续性的限定；（2）具有内在的隐并行性和全局寻优能力；（3）采用概率化的寻优方法，不需要确定的规则就能自动获取和指导优化的搜索空间，自适应地调整搜索方向，从而保证算法向最优解收敛。因此本文利用遗传算法对优化问题P进行求解。

2 基于遗传算法的求解方法

2.1 初始群体

对于优化问题P，考虑任务卸载决策和传输功率分别为整数和实数，所以对其初始群体的染色体采用混合编码方式进行编码。对于N个卸载任务而言，染色体长度为2N，其前半部分采用N个任务编号随机全排列的方式编码，后半部分随机产生0～Pmax间的N个基因。例如5个任务的染色体编码为［2，1，5，4，3；65.8，78.6，56.3，12.6，26.7］，此编码表示在第一道工序中，任务2先加工发射功率为65.8 mW，任务1加工发射功率为78.6 mW，工件5发射功率为56.3 mW，工件4发射功率为12.6 mW，工件3最后加工发射功率为26.7 mW。由此组成遗传算法需要的初始种群。

2.2 适应度函数

适应度函数作为评价个体优劣的标准，适应度越高，则个体越接近最优解，适应度越低，则个体解越差。本文将优化问题P的目标函数取倒数，作为适应度函数来进行计算，即

2.3 选择过程

选择算子的作用主要是避免优良基因的丢失，使得性能高的个体能以更大的概率被选中，有机会作为父代繁殖下一代，从而提高遗传算法的全局收敛性及计算效率，选择操作是建立在群体中个体的适应度评估基础上的。本文根据适应度函数求解种群中全部个体的适应度，采用轮盘赌的方式重新选择个体。若种群的总数为Np，个体j适应度为Fj，则个体j被选中的概率为

由式（13）可见，适应度高的个体被选中进入下一代的概率大，适应度低的个体被选中进入下一代的概率相对较小。

2.4 交叉过程

在遗传算法中，交叉算子是区别于其他优化算法的本质特征，用于组合新的个体，在解空间中快速有效地进行搜索，同时也降低了对有效模式的破坏程度，起到全局搜索寻优的效果［12］。由于初始群体采用混合编码方式，因此针对这两个部分交叉和变异的具体实现有所差别。前半部分是符号编码，采用的是两点交叉；后半部分是实数编码，采用的是算术交叉。

两点交叉，即随机生成两个不同的基因点位，子代1继承父代2交叉点位之间的基因片段，其余基因按顺序继承父代1中未重复的基因；同理，子代2继承父代1交叉点位之间的基因片段，其余基因按顺序继承父代2中未重复的基因。

2.5 变异过程

群体基因的多样性是保证遗传算法寻找到全局最优解的前提条件，然而在进化过程中，遗传选择操作削弱了群体的多样性，上述交叉算子只有满足一定的条件才能保持群体的多样性，而变异操作则是保持群体多样性的有效算子，所以变异操作算子的选取也是必不可少的［12］。前半部分是符号编码，采用的是交换变异；后半部分是实数编码，采用的是非一致性变异。

交换变异，即随机生成两个基因位，并交换两个基因位上的基因。非一致性变异是变异尺度自适应变化的变异算子，在进化初期采用较大的变异尺度来保持群体的多样性，而在后期变异尺度将逐渐缩小以提高局部微调能力，具体如下：设父代染色体为

及每个个体的适应度值都有关，本文Pc和Pm的计算方法如下

其中，f′是要交叉的两个个体中适应值的较大者，f为要进行变异的个体的适应值，k1，k2，k3，k4∈［0，1］。

3 仿真结果与分析

下面对图1所展示的单用户多核服务器的MEC系统的任务卸载调度以及时延和能耗之间的权衡进行仿真，并分析仿真结果。本文讨论在给定传输速率下的系统时延与卸载任务数量的关系，两种卸载策略下的系统时延与卸载任务数量的关系，在给定卸载任务数量下的任务卸载调度的流程、系统时延和能耗之间的权衡。仿真中计算任务的数据量di和所需的计算资源ci都服从均匀分布，即di～U（0，2davg），ci～U（0，2cavg），其中davg=1 kbit，cavg=797.5 cycles/bit。表1列出了仿真所需要的参数及其取值。

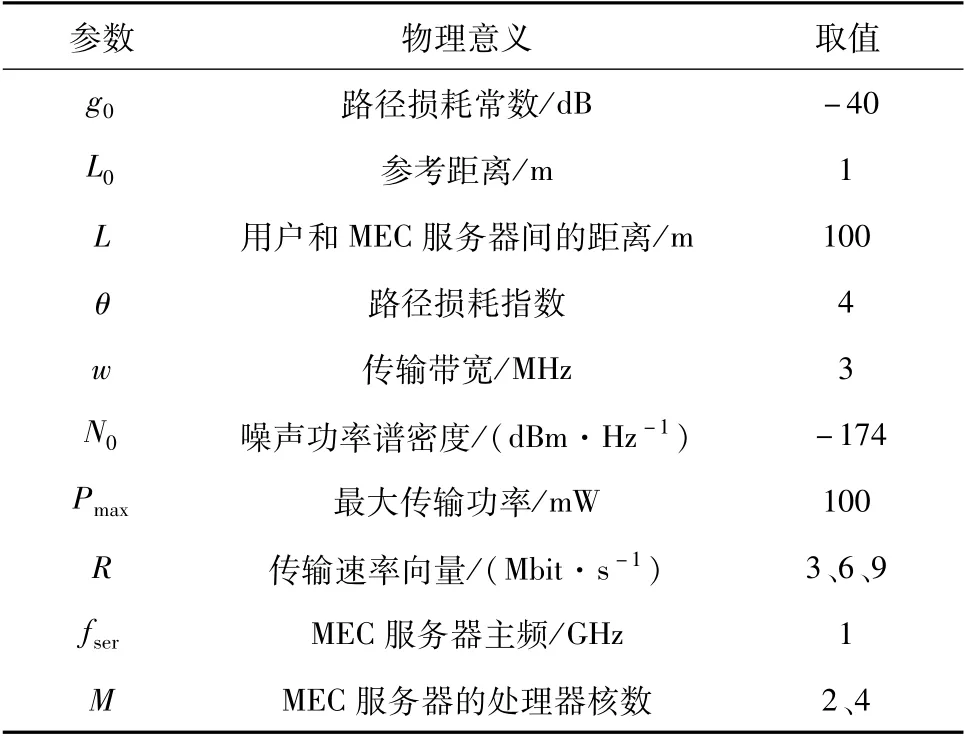
表1 仿真所需参数与取值

图3展示了单用户多核（此处M=4）服务器的MEC系统时延与卸载任务数量关系的曲线，这是在令权重因子η=0时，分别给定传输速率R=9 Mbit/s、R=6 Mbit/s和R=3 Mbit/s下，采用本文的基于混合流水车间调度模型的遗传算法（HFSPGA）得到的卸载策略。由仿真可知，在这三个场景下系统时延总体上随卸载任务数量的增加而增加，并且较大的传输速率对应的系统时延较小。然而，将传输速率从3 Mbit/s增加到6 Mbit/s会显著地减少系统时延，将传输速率进一步从6 Mbit/s增加到9 Mbit/s时，系统时延的减少量就变得很小了。这是因为在前一种情况下，系统瓶颈主要是第一道工序的加工时间过长，工件（任务）送到第二道工序上加工的速度太慢，导致MEC服务器相对充足的计算资源无法充分得到利用，在提升传输速率后，第一道工序的加工时间变短，这些计算资源得以充分利用，从而降低了系统时延；后一种情况下，传输速率很大时，第一道工序的加工时间很短，当工件（任务）更快地送到第二道工序上加工时，这时MEC服务器上的计算资源就相对变得有限，因此系统时延减少并不显著。更为一般的是，无论M为何有限值时，在没有传输速率约束的情况下，在传输速率逐渐增加的过程中，必然会出现上述的这种现象。通过以上分析，可以发现在无线资源和计算资源相对平衡的时候，采用本文的任务卸载策略可以显著地减少系统时延。

图4对比了在两种不同的任务卸载策略下，单用户多核服务器的MEC系统时延与卸载任务数量的关系。图4中HFSP-GA表示本文采用基于混合流水车间调度模型的遗传算法得到的卸载策略，RTOS表示随机任务卸载策略。在给定传输速率向量R=6 Mbit/s的情况下，两种卸载策略的系统时延和任务数量的关系仍符合图3中的规律，即系统时延总体上随任务数量的增加而增加。不论MEC服务器处理器核数为M=2或M=4，基于HFSP-GA卸载策略总比RTOS卸载策略所耗费的系统时延要少；在HFSP-GA卸载策略下，任务数量较少时，节省的时延并不明显，在任务数量较多时，节省的时延也更多。对于前者，这是因为RTOS卸载策略仅仅是在第一道工序上对出现的若干个计算任务随机进行卸载，并没有考虑到系统时延是与第一道工序和第二道工序的加工时间相耦合的，容易出现第二道工序等待加工的时间过长的问题，从而导致系统时延变长；而HFSP-GA卸载策略综合考虑了两道工序的加工时间，确定了合理的任务卸载顺序，从而使得系统时延得以减少。对于后者，这是因为任务数量较少时，系统时延本来就很小，且RTOS卸载策略预测到近似最优卸载策略的可能性比较大，因此采用HFSP-GA卸载策略，系统时延减少不明显；反之，即可解释任务数量较多时，采用HFSP-GA卸载策略系统时延减少量变得更大。

图5展示了在计算任务数N=12，MEC服务器核数M=2，分别给定传输速率R=9 Mbit/s、R=6 Mbit/s和R=3 Mbit/s下任务卸载调度的具体流程。图5中M11表示第一道工序中的第一台机器，即移动设备的发射机，M21、M22分别表示第二道工序中的第一、二台机器，即MEC服务器的两个核。如图5（a）所示，这些计算任务在移动设备发射机上的传输顺序为｛2，11，8，4，12，6，7，1，9，5，10，3｝，在服务器第一个核上的任务处理顺序为｛2，4，12，6，7，9，5，10｝，在服务器第二个核上的任务处理顺序为｛11，8，1，3｝，第二道工序上最后加工完的是任务10，所以任务10加工的截止时间即为系统时延2.053 ms。通过比较图5（a）、图5（b）和图5（c），可以发现图5（c）中计算任务之间服务器有明显的空闲时间，而图5（b）和图5（a）的服务器基本上是不间断地处理任务，只有一开始有略微的等待，这里也就更具体地解释了为什么在图3中将传输速率从3 Mbit/s增加到6 Mbit/s会显著地减少系统时延，而将传输速率进一步从6 Mbit/s增加到9 Mbit/s时，系统时延减少量变得很小。

图6展示了在计算任务数N=20时，单用户多核服务器MEC系统的系统时延和系统能耗之间的权衡。可以发现，系统时延随着η增大而增大，系统能耗随着η增大而减小；在服务器核数为M=2时，系统能耗时延曲线位于M=4时的右侧。前者是因为η越大表示能耗优化的权值更大，从而使传输功率降低，任务的传输时间变长，使得MEC服务器的计算资源得不到充分利用，从而导致系统时延变长；反之亦然。后者是因为服务器计算资源的差异引起的。在服务器核数为M=2和M=4时，系统能耗和系统时延的关系曲线均出现一条垂直渐近线，这表示在系统能耗达到某一点时，如果用更多的能量并不能换取系统时延的显著减少，所以一味地用系统能耗来换取时延的减少必然存在浪费。在服务器核数分别为M=2和M=4，η从10-3（s/J）增至102（s/J）时，系统时延并无显著的增加，因此可取η为102（s/J）时的系统能耗对计算任务进行卸载，从而达到节能的目的。从图6中可以观察到，M=2时能够节能约24.47%，M=4时能够节能约23.6%。

4 结束语

本文研究了在单用户多核服务器的MEC系统中，多个独立计算任务的卸载调度决策和功率分配问题。基于混合流水车间调度模型和遗传算法，对系统时延和系统能耗的加权和优化，获得了最优的任务卸载甘特图；揭示了系统时延随任务数量增加而增加的关系，通过分析发现在无线资源和计算资源相对平衡时，采用本文的任务卸载策略可以显著地减少系统时延；接着，与随机任务卸载策略相比，同样条件下本文所提出的卸载策略的系统时延较小；最后，分析了系统能耗和系统时延成反比的关系，在不增加系统时延的条件下找到了一种节能的方式。