基于神经元网络PID整定的电液位置伺服系统

何文清　麦云飞

摘 要：基于汽车疲劳试验机平台对转向机液压伺服系统进行研究，针对试验机运行过程中出现的控制精度不高、系统不稳定问题，设计了电液位置伺服系统。首先建立系统数学模型，推导相应的传递函数。接着利用Simulink软件对系统进行稳定分析，利用典型的PID参数整定策略对系统进行优化处理。最后采用神经元网络自学习算法，在simulink中设计单神经元PID自学习系统，对位置伺服系统进行参数优化整定。研究结果表明：采用单神经PID整定的电液位置伺服系统超调量比典型PID整定策略减少了90%以上，整定时间也缩短了一半以上。系统稳定性更强、精度更高，具有更好的鲁棒性。

关键词：电液位置伺服系统;Simulink软件;单神经元PID整定

DOI：10. 11907/rjdk. 191622

中图分类号：TP319   文献标识码：A                文章编号：1672-7800（2020）003-0177-05

Electro-hydraulic Position Servo System Based on Neural Network PID Tuning

HE Wen-qing，MAI Yun-fei

（School of Mechanical Engineering， University of Shanghai for Science and Technology， Shanghai 200093，China）

Abstract： This paper mainly studies the hydraulic servo system of steering gear based on the automobile fatigue testing machine of an enterprise as a platform. During the operation of the test machine， the control accuracy is not high and the system is unstable. According to the design requirements， the electro-hydraulic position servo system is designed at first. Then the stability of the system is analyzed by Simulink software， and the system is optimized by typical PID parameter tuning strategy. Finally， a single neuron PID self-learning system is designed in Simulink by using the self-learning algorithm of neuron network to optimize the parameters of the position servo system. The results show that the overshoot of electro-hydraulic position servo system tuned by single nerve PID is reduced by more than 90% and the setting time is shortened by more than half compared with the typical PID tuning strategy. The system has stronger stability， higher accuracy and stronger robustness.

Key Words： electro-hydraulic position servo system; Simulink software; single neuron PID tuning

0 引言

電动助力转向机电一体化试验台[1-2]是用于模拟汽车转向时所受地面摩擦等负载的模拟加载平台，可对汽车电动助力转向设备进行性能分析。电液位置伺服系统[3-4]是试验台控制器的重要组成部分，具有输出功率大、响应速度快、精度高等特点。由于液压伺服系统在运行过程中会出现物理参数（温度、尺寸、压力等）改变，或者受到外界干扰，导致无法达到理想的控制要求，因此学者们使用不同方法优化电液位置伺服系统。李辉[5]指出在系统中使用PID控制器可以达到较好的效果;孔令刚[6]把复合PID控制器应用到电液伺服系统中，同样取得了不错的效果;裴雨霞[7]利用模糊控制理论与PID控制器相结合的方法来对电液位置伺服系统进行优化，此方法相比传统PID方法整定能力更强，整定时间更短;车江鸽[8]也使用模糊控制理论优化系统参数;马淑可[9]指出可把遗传算法与PID控制相结合完成系统参数优化;侯艳艳等[10]把遗传算法运用到电液伺服系统仿真中。神经元网络算法作为新的控制策略可以通过自学习、趋势逼近等特点，有效解决复杂的非线性模型问题。王敬志、刘伟、刘迪、张学燕等[11-14]都对神经元网络PID控制技术进行了研究。本文将神经元网络算法结合PID控制器运用到电液位置伺服系统进行智能控制。为了使仿真模型搭建简便，采用基于单神经元网络PID整定方法对电液伺服位置系统进行研究。通过与经典PID控制策略比较，发现单神经元PID整定控制精度高，整定时间短。相比模糊控制和遗传算法控制方法，单神经元网络PID整定可以作为很好的替代，并且使用范围更广，接受程度更高。

1 建模分析

如圖1所示，右下端的指令电位器发出信号指令，信号指令与实际缸体位置信号进行对比变为误差，误差在放大器被放大，电液伺服阀接收被放大的误差信号后进行信号转换，将电信号转换为液态流量信号发送给液压缸，使之调整位置。传感器不断发送误差信号，液压缸也不断改变位置，直到现有位置与预设位置信号相等，最后液压缸停止改变位置。

根据图2可知，系统中指令电位器发送指令（类似电脑），通过电位器对外发出信号指令，D/A 转换器将实际位置信号变成电信号。信号收集设备是位移传感器，此时传感器将测得的位置信息转化为可以比较的电信号，和电位器发出的信号进行比较，两点信号的差值就是误差信号。不断发送和检测的过程形成闭环系统，最后通过不断改进位置达到理想的位置结果。

当系统执行元件的固有频率高于50Hz时，把伺服阀看成振荡环节，一般情况下都是二阶，其数学模型[16]表述为：

式中：[Kv]表示伺服阀增益，[ωv]表示固有频率，[ξv]表示伺服阀阻尼比。

液压缸油液的液压能转换成直线运动的机械能，不停做直线往返运动。液压输出是活塞杆位移量，其传递函数为：

式中：[Kq]表示液压缸滑阀流量增益，[Ap]表示液压缸活塞面积，[Kc]表示滑阀流量压力系数，[ml]为负载质量。

放大器、传感器传递函数在进行建模中看成是比例环节，传递函数分别为：

式中：Ka为伺服放大器比例增益，Kf为位移传感器增益。

根据以上传递函数整理得到系统的开环传递函数为：

伺服放大器比例增益为 [Ka]=100 A/V，伺服阀增益为 [Kv]=1.96×10-3 m3/（A·s），位移反馈系数为[Kf]=1 V/m，液压缸活塞面积为[Ap]=1.3×10-2 m2，液压缸滑阀流量增益为[Kq]=2.01 m2/s，滑阀流量压力系数为 [Kc]4.6×10-10 m5/（W·s），伺服阀固有频率为[ωv]=100 Hz，阻尼系数为[ξv]=0.65。由 MATLAB/Simulink[5-6] 可建立系统闭环传递函数模型，如图 3所示。

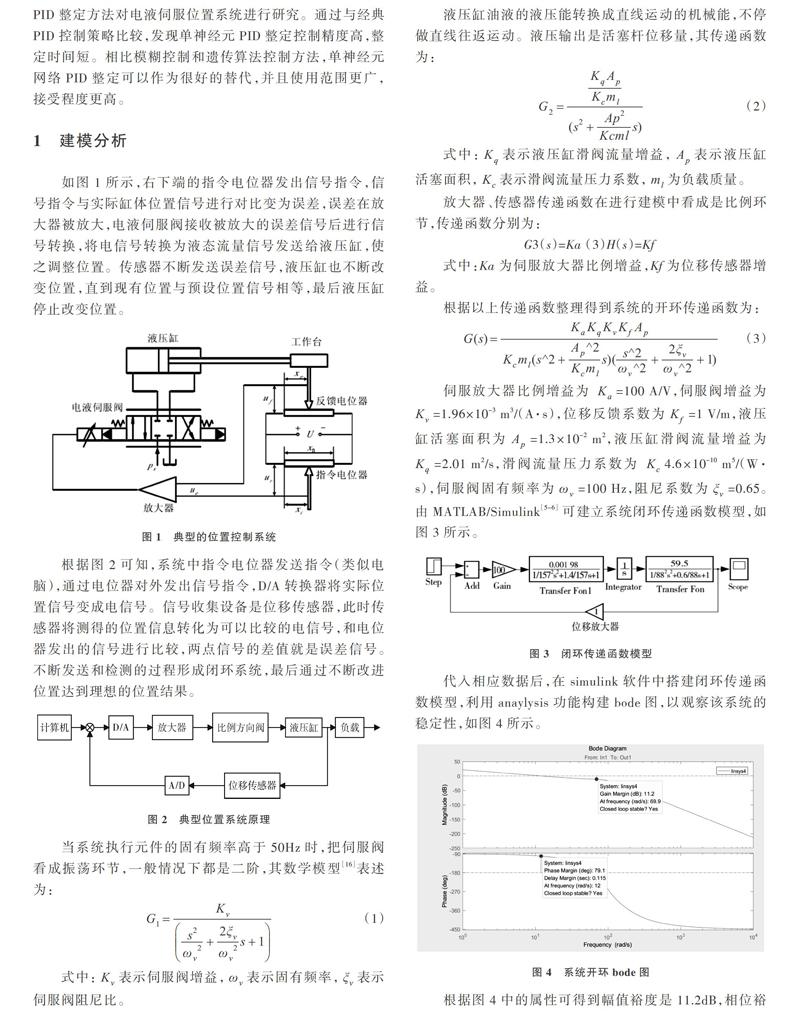
代入相应数据后，在simulink软件中搭建闭环传递函数模型，利用anaylysis功能构建bode图，以观察该系统的稳定性，如图4所示。

根据图4中的属性可得到幅值裕度是11.2dB，相位裕度为[79.1°]。要求可知系统的幅值裕度需大于6dB，而相位裕度在[30°～70°]，从而可以看出此系统的相位裕度大，系统最终不能达到稳态，所以必须进行改进使系统达到理想要求。

2 传统PID控制策略

首先采用PID控制器单独作用电液伺服位置系统实现优化控制效果。

将一个比例环节（p）、一个积分环节（i）和一个微分环节（d）线性组合成调节控制量，实现对控制对象的调节。PID控制系统结构如图5所示。

给定输入值[e（t）]和输出值[y（t）]，定义系统误差[e（t）]：

PID控制规律可表示为：

写成传递函数形式：

经离散变换后的形式为：

增量表达式为：

式中：[u（t）]——控制器输出量，[kp]——控制器的比例系数 ，[TI]——控制器积分时间常数 ，[TD]——控制器的微分时间常数，[KI=KPTI]，控制器积分系数，[KD=KPTD][a2+b2]，控制器微分系数，T——采样周期，K——采样序号。

比例环节可使系统快速完成响应，通过改变比例参数降低系统偏差。使用过大的比例参数会产生过大的超调量，系统变得不稳定，因此选用合适的比例参数很重要。

积分环节可以消除静态误差。[TI]越大，静态误差消除时间越长，但能够减少系统超调，使系统不容易产生振荡;[TI]越小，消除静态误差时间越短，但容易造成系统振荡。

微分环节的微小改变可以影响整个系统控制，减小由前两种控制环节产生的超调量，最终达到提高系统稳定性目的，但容易受到干扰信号影响。

根据3种控制环节性质，在得到被控制对象精确的数学模型后，通过选择合适的PID参数，可以对被控系统实现精确控制。而某一种控制环节参数选择不合适都会造成无法精确控制，所以PID控制策略即是如何选择参数[Kp]、[KI] 、[KD]。表1显示3种控制参数的变化对系统控制效果的影响。

系统调试过程中，通常需要花费大量的时间和精力寻找最优[Kp]、[KI]、[KD]参数。经过大量参数调试，最终取得[Kp]、[KI]、[KD]的参数分别为2.013，0.056 0，-0.015 0。利用经典PID策略调试后的阶跃图与原阶跃图比较如图6所示。

由图6可知，经过经典PID参数整定后的系统稳定性高、响应较快，且精度较高，但有0.27超调量，因此需采用深度学习解决控制问题。

3 基于s函数的单神经元PID控制方法

3.1 单神经元控制及其算法

利用单神经网络学习方法[17-18]与常见的 PID 控制联系在一起，可以有效处理一些比较棘手的参数整定以及学习过程中较难控制和捕捉的参数问题。传统PID 连续控制规律如下：

增量式PID 控制方法如下：

单神经元网络 PID 整定如图7所示。

单神经元整定过程量由转换器输出，[u（k）]通过自适应学习形成，[yr]为预设值，[y（k）]为自适应学习量处理结果。经过转换器后变为系统学习所需的过程量： [x1（k），x2（k），][x3（k）]，如下式所示。

式中：[Z（k）=yr（k）-y（k）]为系统递进信号;[w1（k），][w2（k），][w3（k），]对应[x1（k），x2（k），x3（k）]的权值系数;K为神经元比例系数，K>0。

3.2 有监督的 Hebb 学习算法

神经网络学习规则即为调节神经元之间连接权值的规则。本文选用有监督的 Hebb 学习规则：

其中[ηi]是单神经元自适应学习的学习速率。

通过对上述公式整理，可以规范控制方法的收敛性与鲁棒性：

3.3 S 函数编写

在S函数模块[19]中不能直接对单神经网络控制进行模拟，因此采用 S 函数在MATLAB工作区域编写 S 函数后放入S函数模块进行运行完成自学习过程。在工作区域编写关于S函数的程序代码如下：

function[sys，x0，str，ts]=neuron2（t，x，u，flag）

switch flag，

case 0， [sys，x0，str，ts] = mdlInitializeSizes;

case 2， sys=mdlUpdate（t，x，u）;

case 3， sys = mdlOutputs（t，x，u）;

case {1，4，9}， sys = [];

otherwise ，error（[‘Unhandled flag = ，num2str（flag）]）;

end;

function [sys，x0，str，ts]=mdlInitializeSizes

sizes = simsizes;

sizes.NumContStates = 0;

sizes.NumDiscStates = 3;

sizes.NumOutputs = 4;

sizes.NumInputs = 4;

sizes.DirFeedthrough = 1;

sizes.NumSampleTimes = 1;

sys = simsizes（sizes）; x0 = [2.0120 0.0556 -0.128];

str = [];ts = [-1 0];

function sys = mdlUpdate（t，x，u）

sys（1） =x（1）+500*u（1）*u（4）*u（1）;

sys（2） =x（2）+500*u（1）*u（4）*u（2）;

sys（3） =x（3）+500*u（1）*u（4）*u（3）;

function sys = mdlOutputs（t，x，u）

xx= [u（1）-u（2） u（1） u（1）+u（3）-2*u（2）];

sys=[u（4）+0.1*xx*x/sum（abs（x））;x/sum（abs（x））];

单神经元网络学习方法需要提前设置学习参数，将3个控制参数设置为（2.013，0.0560，-0.0150），设置的采样时间为0.001s。根据神经元公式预设学习速率分别是[η1=500，η2=500，η3=500] 。搭建单神经元自适应模型如图 8 所示。

4 研究不足与展望

本文提供了一种基于神经元网络pid参数整定的电液伺服系统。根据多次实验可以发现神经网络算法处理信息的原理是依靠系统的复杂程度，调整内部节点之间相互连接的关系。神经网络控制能够充分逼近任意复杂的非线性系统;能够学习和适应严重不确定系统的动态特性;具有很强的鲁棒性和容错性;用并行分布处理方法，能够快速地进行大量运算 。

然而神经网络最严重的问题就是没有能力来解释自己的推理过程和推理依据;不能向用户提出必要的询问，因此当数据不充分时，神经网络就无法工作;神经網络将一切问题的特征变为数字，把一切推理变成数值计算，结果势必会丢失信息。

本论文在得出控制算法获得整定结果后无法解释推理过程，只能通过数字图像进行呈现，因此要求我们尝试更多适合的智能算法来解决同等的问题。

针对电液伺服系统等非线性，精确度较低的系统，我们可以关注其他不过分依赖于模型的精确程度、适用于具有重复性运动系统的算法进行优化，比如迭代学习算法等。希望在以后的学习和研究中可以利用类似方法来解决现实中的相关模型。

5 结语

通过分析，运用经典PID参数整定策略虽然可以得到初步的PID参数，然而控制效果不完美，超调量大，参数整定时间长。如图9所示，利用S函数并搭建单神经元PID自适应的控制方法，可最终得到稳定的控制参数。根据阶跃响应，可显示经典PID控制超调量为0.27，自适应方法的超调为0.02，减小了0.25的超调量，降低了92.5%左右。此外，经典PID策略往往调控时间很漫长，不能一开始就获得整定参数，而单神经元网络PID整定除了搭建系统和编辑S函数外，所用时间不多，可节省一半以上时间。研究发现，对于这种高阶非线性控制系统可使用像单神经元网络自适应的深度学习方法实现快速、有效的参数整定，从而提高系统控制性能[20-22]。

参考文献：

[1]王海博，骆艳洁. EPS转向机主动加载系统研究[J]. 电子科技，2017，11（30）：45-47

[2]左智飞. 电液伺服阀试验台的开发与研究[D]. 广州：广东工业大学，2014.

[3]刘丹丹，骆艳洁. EPS疲劳试验台电液位置系统建模与分析[J]. 通信电源技术，2015，32（5）：87-89.

[4]肖旺，刘军营，刘新钊，等. 基于AMESim的高速注塑机液压伺服系统的仿真研究[J]. 机床与液压， 2013（24）：197-201.

[5]李辉，史荣珍.  PID控制器参数整定与分析[J]. 电脑知识与技术，2019（15）：243-245.

[6]孔令刚，麦云飞. 复合PID算法应用于转向器疲劳试验台[J]. 机械工程与自动化，2015，189（2）：183-184.

[7]裴雨霞. 电液伺服疲劳试验机的设计与仿真[D]. 长春：长春理工大学，2014.

[8]车江鸽，骆艳洁. EPS试验台模糊PID控制器设计[J]. 制造业自动化，2012，33（12）：1-3.

[9]马淑可，麦云飞. 基于遗传神经网络 PID 整定的电液位置伺服系统[J].  农业装备与车辆工程，2018（9）：67-70.

[10]侯艳艳，曹克强，胡良谋，等. 采用遗传 PID 整定的电液伺服系统仿真研究[J].  现代制造工程，2012（5）：74-77.

[11]王敬志，任开春，胡斌. 基于BP神经网络整定的PID控制[J]. 工业控制计算机，2011，24（3）：72-73.

[12]刘伟. 基于蚁群优化的神经网络智能 PID 控制策略研究[D]. 秦皇岛：燕山大学 ，2010.

[13]刘迪. 基于神经网络的 PID 控制算法[D]. 哈尔滨：黑龙江大学，2008.

[14]张学燕，高培金，刘勇. BP 神经网络 PID 控制器在工业控制系统中的研究与仿真[J]. 自动化技术与应用，2010，29（5）：9-12.

[16]MAI Y F，LIU S L，DING W J. Design and matlab simulation of a composite pid controller for EPS test-benches[C].  Appl.Mech.Mater Mechanical Structures and Smart Materials. Switerland： Trans Tech Publi- cations Ltd，2014（487）：635-638.

[17]杨敏. 电子万能材料试验机单神经元 PID 控制系统研究[D]. 扬州：扬州大学，2012.

[18]DONG W，QU D，DONG W. A PID neural network control strategy based on GA-BP algorithm[J]. Binggong Zidonghua/ Ordnance Industry Automation， 2011， 30（2）： 66-69.

[19]徐杭东，麦云飞. 基于神经网络的液压材料试验机系统自适应 PID 控制研究[J]. 机电工程，2018（4）：375-379.

[20]魏跃斌，陈惠贤，张小奇. 基于先进PID控制的液压同步系统研究[J]. 液压气动与密封，2016（1）：20-22.

[21]車高峰. 基于神经PID的网络化控制系统的设计[J]. 电脑与电信，2012（4）：33-35.

[22]朱逢锐，林玉娥. 基于RBF 神经网络的PID自校正控制研究[J]. 电脑知识与技术，2016，12（25）：155-157.

（责任编辑：杜能钢）

收稿日期：2019-04-28

作者简介：何文清（1994-），男，上海理工大学机械工程学院硕士研究生，研究方向为液压伺服系统;麦云飞（1962-），男，硕士，上海理工大学机械工程学院副教授、硕士生导师，研究方向为液压伺服系统。