WSN中基于Mini Batch K-Means与SVM的入侵检测方案
欧阳潇琴 王秋华

摘 要:无线传感器网络通常部署在复杂的户外环境,易遭受各种攻击。多数入侵检测系统均采用数据挖掘算法对网络数据包进行分析,但在处理大样本集时,其效率明显降低。针对这一缺点,提出一种基于Mini Batch K-Means和SVM的入侵检测方案。该方案首先分别对正常行为特征库和异常行为特征库进行Mini Batch K-Means聚类,取得类中心作为各类的代表样本并赋予权值,将其传入SVM分类器作为训练数据,得到分类超平面,通过该超平面对待测样本作出判断。解决了如K-Means、KNN、SVM等传统数据挖掘算法在大数据样本集数据分析中面临的低效问题。仿真结果表明,该方案能快速准确地判断样本类别,其检测率达到98.7%。与K-Means、KNN和SVM相比,不仅达到了同样高的检测率,而且明显提高了入侵检测的时间效率。
关键词:无线传感器网络;入侵检测;Mini Batch K-Means聚类算法;SVM算法
DOI:10. 11907/rjdk. 191638
中图分类号:TP309 文献标识码:A 文章编号:1672-7800(2020)003-0204-06
An Intrusion Detection Scheme Based on Mini Batch K-Means and
SVM in Wireless Sensor Networks
OU YANG Xiao-qin1,WANG Qiu-hua2
(1. School of Communication Engineering,Hangzhou Dianzi University;
2. School of Network Space Security,Hangzhou Dianzi University, Hangzhou 310018, China)
Abstract: Wireless sensor networks (WSN) are usually deployed in complex outdoor environments and vulnerable to various attacks. Most intrusion detection systems use data mining algorithms to analyze network packets, but their efficiency is significantly reduced when dealing with large sample sets. In view of this shortcoming, a intrusion detection scheme based on Mini Batch K-Means and SVM is proposed. The scheme firstly conducts Mini Batch K-Means clustering on the database of normal behavior and abnormal behavior. The obtained centers of clusters are then used as representative samples of their clusters, each of which is assigned a weight and is input into SVM classifier as training data, so as to get a Classifying hyper-plane which can be used to classify samples. The proposed scheme solves the inefficiencies that traditional data mining algorithms such as K-means, KNN and SVM face in data analysis of big data sample sets. Simulation results show that our proposed scheme can determine the sample types quickly and accurately, whose accuracy is 98.7%. Compared with K-Means, KNN and SVM, our proposed scheme not only achieved the same accuracy, but also improved the time efficiency of intrusion detection significantly.
Key Words: wireless sensor networks; intrusion detection; mini batch K-Means clustering algorithm; support vector machine algorithm
0 引言
近年來,随着无线传感器网络(WSN:Wireless Sensor Networks)应用的日益普及,与之相关的安全问题也随之而来。WSN通常部署在相对复杂、无人维护的环境中,其所面临的安全威胁更加复杂多样,除一般无线网络所面临的信息泄露与篡改、拒绝服务、重放等多种攻击外,WSN还面临着传感器节点被攻击者物理捕获,并获取节点中存储的重要信息从而控制网络的威胁。WSN中的入侵行为能够造成网络瘫痪、数据欺骗等安全问题,并给网络带来巨大破坏[1]。因此,WSN安全是一个亟待解决的问题,WSN的入侵检测具有重大研究意义,得到了广泛研究,已提出多种入侵检测算法[2-7]。
文献[2]采用基于改进粒子群优化的K-Means算法,根据物理层的接收信号强度 (RSS:Received Signal Strength)检测欺骗攻击;文献[3]利用从不同接收节点获取的RSS比率值检测欺骗攻击。但上述两种方案均无法检测出节点是否遭受到物理捕获攻击。文献[4-5]使用基于欧氏距离的KNN算法,通过投票检测入侵行为;文献[6]通过带有聚类半径的K-Means算法对特征向量进行入侵检测;文献[7]采用改进核函数的支持向量机(SVM:Support Vector Machine)算法将线性不可分的向量映射到高维空间,从而得到分类超平面,对待测样本进行预测。但是文献[4-7]所提方案在处理大样本集时计算量大,耗时长、效率低,而随着网络的发展,必然会有更多数据加入训练集,算法训练时间也会随之增加[8]。
本文针对上述入侵检测方案中存在的缺陷,提出一种分别对正常行为特征库和异常行为特征库进行聚类处理,再使用SVM算法对样本进行分类预测的入侵检测方案。在本文所提方案中,首先使用适合大数据的聚类算法Mini Batch K-Means对大样本集进行数据简约,即对不同行为特征库进行聚类,得到每类的聚类中心作为该类的代表样本,该类的样本数量作为代表样本的权值;然后,将代表样本和其对应的权值作为SVM分类算法的训练数据,经过训练得到一个超平面,最后利用该超平面对正常样本和异常样本进行分割,从而对待测数据进行预测,判断其是否属于正常行为。本方案的主要优点为:①对样本进行Mini Batch K-Means聚类并取类中心作为训练数据,有效解决了大样本集所引起的耗时影响,显著提高了检测速度;②分别对两种行为特征库进行聚类处理保证了聚类得到的类中心代表的都是同一类行为,同时对类中心赋予权值,保证了较高的检测准确率。本文对方案进行了算法实现,实验结果表明,使用Mini Batch K-Means显著提高了样本聚类时的收敛速度,成倍提高了SVM分类速度,同时保证了较高的检测准确率,得到了良好的检测结果。
1 数据挖掘在入侵检测中的应用
数据挖掘[9]是指使用机器学习、统计学等领域的技术从海量数据中挖掘隐藏信息,将其转化成有用知识。数据挖掘过程大致分为5个阶段:问题定义、数据收集、数据预处理、数据挖掘实施以及挖掘结果解释与评估[9]。在明确数据挖掘任务以及目标数据对象后,使用分类、回归等方法对已得数据进行分析,从数据源中抽取与数据挖掘目标相关的信息。
由于数据挖掘能够从大量数据中提取特征,挖掘出特定的行为模式,因此,该技术也常被用于入侵检测中[10-14]。通过对网络通信时采集而来的数据包进行分析,提取出其中隐含的规律,从而得出正常类型和攻击类型的数据包特征。
WSN由大量的小型传感器组成,通过部署在监测区域的传感器采集数据并发送给监察者,可从数据包中提取节点RSS值、感知数据值、数据包接收比例和发送比例、丢包率、延迟时间、节点剩余能量等特征组成的特征向量,作为数据挖掘样本,使用数据挖掘算法对上述特征向量进行分析,对于每一个收到的数据包,判断其是否异常。基于数据挖掘的入侵检测模型如图1所示。
2 算法基础
2.1 Mini Batch K-Means
Mini Batch K-Means算法[15-16]是K-Means算法的变种,采用随机产生的小批量数据子集进行聚类,大大减少了计算时间,Mini Batch K-Means算法产生的聚类效果只略差于K-Means算法。
Mini Batch K-Means算法流程如下:
(1)首先随机初始化K个样本作为K个簇初始质心。
(2)在第t次迭代中,从数据集中随机抽取一些数据形成小批量样本集,求其到各中心的距离,将该样本集归到距离最短的中心所在的类。
(3)利用均值方法更新该类的中心值。
(4)对于所有的K个聚类中心,如果利用步骤(2)和步骤(3)的迭代方法更新后,目标函数值保持不变,则迭代结束,否则继续迭代。
样本间的距离采用欧式距离,欧氏距离是指两点之间的欧氏空间直线距离。两点[u=(u1,u2,?,un)]和[v=][(v1,v2,?,vn)]之间欧氏距离计算如式(1)。
第i个类中心计算公式如式(2)。
其中,[ciq]表示第i个类的类中心,[Ni]表示第i个类中的元素个数,[Ci]表示第i个类。
加入批量大小为batch_size的小批量样本集[X=][X1,X2,?Xbatch_size]后的类中心为[c′iq],计算方式如式(3)。
另外,使用误差的平方和(Sum of the Squared Error, SSE)作为度量聚类质量的目标函数,SSE定义如式(4):
2.2 支持向量机
支持向量机[17-18]是一种监督式学习方法,广泛应用于统计分类及回归分析,其特点是能够同时最小化经验误差与最大化几何边缘。SVM可以很好地用于高维数据,避免维数灾难。其基本思想是将输入向量映射到高维特征空间,然后在特征空间构造最优分类超平面,向量集合被该最优超平面分开。最优分类超平面如图2所示,[x=][(xi,yi)i=1,2,?,n]为训练样本,n为样本数量,[xi]为输入向量,类别[yi∈(0,1)]。
所有分类超平面可表达为式(5)。
其中,“[w]”代表超平面的法向量,參数[bw]决定超平面从原点沿法向量的位移。
决策函数为式(6)。
由于要阻止数据点落入边缘内,因此添加如下约束:
(1)对于属于第一类别的[xi],有[wT?xi-b1]。
(2)对于属于第一类别的[xi],有[wT?xi-b-1]。
支持向量到分类间隔距离的函数间隔定义为[γ=y(wT?x-b)=yfx]。[wT?x-b=1]与[wT?x-b=-1]两个平面之间的距离为[margin=2w=2γ],则有[γ=1w],且[yi(wT?xi-b)1]。SVM分类的关键为最大化margin,等价于最小化[w22],目标函数可转化为式(7)。
引入拉格朗日乘子[αi>0,(i=1,2,?,n)],构造拉格朗日函数如式(8)。
根据拉格朗日对偶性,原始约束最优化问题可等價于极大极小对偶问题:[maxLw,b,α]。等价于式(9)中最优化问题。
由此得到算法决策函数如式(10)。
3 基于Mini Batch K-Means和SVM的融合算法设计
3.1 算法思想
Mini Batch K-Means算法和K-Means算法都属于聚类算法,但由于K-Means算法在对大样本集进行聚类时的收敛速度较慢,因此本方案采用适用于大样本集的Mini Batch K-Means算法进行聚类,在基本不影响聚类效果的前提下,可以显著提高收敛速度。SVM算法的中心思想是将线性不可分的数据映射到高维空间,再在空间中构造一个最优分类超平面将两类数据分隔开,减少异类之间的相互影响。
鉴于入侵检测的样本集十分庞大,采用传统聚类算法或SVM等机器学习算法进行检测非常耗时,本文所提方案着重解决入侵检测中大样本集所带来的耗时问题。本方案先采用Mini Batch K-Means对训练样本进行快速聚类,获取类中心,将其作为SVM分类器的训练数据,然后构造分类超平面,再根据该超平面对待测样本进行分类预测。
3.2 检测流程
本文方案的检测流程包括去重处理与样本划分、Mini Batch K-Means聚类、簇中心提取和SVM分类4个步骤。
(1)去重处理与样本划分。当网络状况和被监测区域环境处于一个相对稳定的状态时,会出现一部分数据包提取到相同样本,大量重复的样本会在一定程度上影响算法运行速度。通过去重处理并给每一个样本赋予一个权重,可以减轻样本重复所带来的不利影响。首先,给每个样本赋予一个权重weight,初始值为1,将每一列属性值都相等的样本合并到一个样本,相应weight赋值为该样本代表的重复样本数量;然后,根据样本标签将训练样本划分到正常行为特征库或异常行为特征库,如图3所示。
(2)Mini Batch K-Means聚类。分别对正常行为特征库和异常行为特征库中的数据进行Mini Batch K-Means聚类。Mini Batch K-Means算法中有两个参数至关重要,分别是聚类簇数K和批量大小batch_size。K表示聚类目标簇的数量,即根据算法规则将样本分配到K个簇中;batch_size表示每次迭代时从数据集中随机抽取的样本批量大小。每次迭代时,随机抓取batch_size个数据元素[S=s1,s2,?,sbatch_size],计算其加权平均值[Avg=][i=1batch_sizewi?sii=1batch_sizewi],再计算平均值[Avg]与K个簇中心的欧氏距离[D=d1,d2,?,dk],得到最小距离[mind1,d2,?,dk],将抓取的数据分配到距离最近的簇中。按照上述迭代方法,分别将正常特征库和异常特征库中的样本划分为大小均衡的K个簇,如图4所示。
(3)簇中心提取和权重分配。由步骤(2)得到K个簇,从每个簇中提取其簇中心作为该簇的代表样本。假设第i个簇中含有m个数据元素[s1,s2,?,sm],每个元素对应的权重分别为[w1,w2,?,wm],其簇中心[Ci=j=1mwj?sjj=1mwj],权重[Wi=j=1mwj]。按照上述方法计算得到K个簇中心[C1,C2,?,Ck]及其对应权重[W1,W2,?,Wk],如图5所示。
(4)SVM分类。由步骤(3)得到K个簇中心及相应权重,将其作为SVM分类器的训练数据和样本权重,采用高斯径向基函数作为SVM的核函数,将线性不可分的样本映射到高维特征空间,从而得到一个分类超平面[w?x-b=0],以及决策函数[fx=sgnw?x-b]。使用上述分类超平面,对待测样本进行分类,如图6所示。设待测样本为[x=x1,x2,?,xn],计算[fx]。若[w?x-b>0],则该样本属于正常类别;若[w?x-b<0],则该样本属于异常本方案整个执行流程如图7所示。
4 性能仿真
4.1 仿真说明
本方案的仿真数据采用UCI数据集中的KDD99[19-21],该数据是由美国国防部高级规划署在MIT林肯实验室模拟的美国空军局域网的一个网络环境中经过9周时间,仿真各种用户类型、各种不同的网络流量和攻击手段收集而来的数据集,是目前公认的入侵检测数据集。本文使用10%的数据集作为测试数据,共有近50万条,包含正常数据和异常数据两大类数据集,其中异常数据集分为DoS(Denial of Service)、U2R(User to Root)、R2L(Remote to User)和Probe 4类攻击数据。本方案所使用的实验环境为Windows 10系统、i5处理器,4核CPU,8G内存。
首先需对数据进行预处理,使用出现频率最高的数值填补缺失值,对于标称型数据,根据其取值在取值空间中的频率,将其量化到[0,1]区间。对数据进行PCA降维处理,去除部分没有价值的属性,再对所有属性进行Z-score中心化处理。处理方式如式(11)。
其中,mean表示每个属性的均值,varience表示属性的标准差。中心化处理是为了避免计算欧式距离时大数吃小数的问题。
4.2 结果分析
4.2.1 聚类效果分析
在给定相同数量数据样本情况下,分别使用K-Means和Mini Batch K-Means方案对样本进行聚类。图8为两种算法的收敛时间对比,图9为聚类适应度inertia对比。收敛时间表示聚类时长,inertia为各样本到其所属类中心的距离平方和,是代表聚类适应度的指标,计算如式(4)所示,inertia越小,聚类效果越好。
由图8可以看出,Mini Batch K-Means方案的收敛时间远小于K-Means,因为前者在每次迭代过程中都是抓取一个批量的樣本集进行划分,而K-Means每次只针对一个样本进行聚类,样本集越大,两者对比越明显。
由图9可以看出,Mini Batch K-Means的聚类适应度inertia只稍大于K-Means,结合图8可知,Mini Batch K-Means在基本不影响聚类效果的情况下显著提高了收敛速度。
4.2.2 入侵检测结果分析
表1给出了本方案的仿真结果,表中4列分别表示测试样本的攻击类型、用于测试的样本总数、从总样本中检测出的正确样本数量以及各种攻击类型的检测百分比。由表1可知,本方案对各种攻击样本都有比较良好的检测效果。
本方案使用聚类中心作为一个类的代表样本,即将相似度较高的样本融合成一个样本,再赋予权重,从而降低大样本集所带来的耗时影响。因此,聚类簇数的大小对检测精度会有一定影响。图10为不同聚类簇数下本方案的检测率。结果表明,聚类簇数越大,准确率越高。但是,聚类簇数的增加,也会直接影响聚类时长,图11为不同聚类簇数的大小对检测时间的影响。结果表明,聚类簇数越大,入侵检测的时间开销也越大。
结合图10和图11可知,增加聚类簇数,可以增加检测精度,但同时也会加长数据训练时间。因此,需要经过不同参数验证,得到一个最合适的聚类簇数,使得本方案既有一个良好的检测率,又不会明显增加时间开销。此处通过实验选择1 000作为较为合适的聚类簇数。
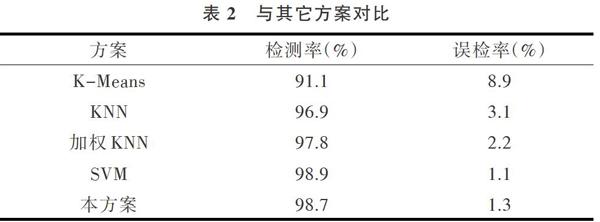
表2给出了本方案与K-Means、KNN、加权KNN、SVM 4种方案在相同测试样本下的检测率对比,由表2可知,相对于其它几种方案,本方案具有更高的检测率和更低的误检率。
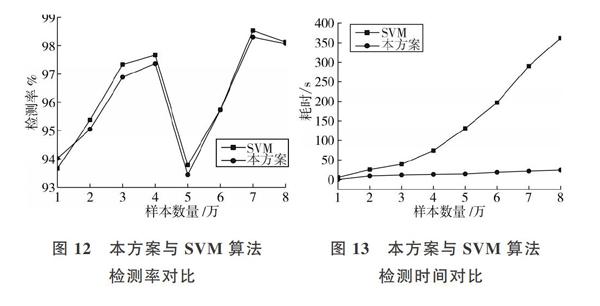
图12显示了本方案与SVM算法在相同训练样本数量下的检测率比较。由图12可知,本方案的检测率稍低于SVM的检测率。
图13为本方案与SVM算法在相同训练样本数量下检测所耗费时长对比。由图13可知,本方案的时间开销明显低于SVM算法。
综合图12和图13可知,本方案在保证理想检测率的前提下,显著提高了大样本集下的检测速度。
5 结语
本文针对传统数据挖掘算法在分析大样本集时耗时较大、效率较低的问题,提出了一种基于Mini Batch K-Means和SVM的入侵检测算法。利用Mini Batch K-Means算法分别对正常行为特征库和异常行为特征库快速聚类,取得类中心作为SVM分类器的训练样本,得到分类超平面对待测样本作出判断。仿真结果表明,本方案在时间开销上具有明显优势,并且具有理想的检测效果。但该算法仍存在无法识别出具体攻击类型的缺陷,有待今后进一步研究。
参考文献:
[1]钟敦昊, 张冬梅, 张玉. 一种基于相似度计算的无线传感器网络入侵检测方法[J]. 信息网络安全, 2016(2):22-27.
[2]陶莉,孙子文. 无线传感器网络KIPSO欺骗攻击检测模型[J]. 传感技术学报, 2016, 29(7):1049-1055.
[3]WANG W, WANG Z. Anti-Sybil attack MPRR-RSSI localization algorithm in wireless sensor networks[J]. Journal of Electronic Measurement & Instrumentation, 2016.
[4]MA Z,KABAN A. K-Nearest-Neighbours with a novel similarity measure for intrusion detection[C]. 2013 13th UK Workshop on Computational Intelligence, 2013:266-271.
[5]JAMSHIDI Y,NEZAMABADI-POUR H. A Lattice based nearest neighbor classifier for anomaly intrusion detection[J]. International Journal Of Applied Mathematics And Computer Science,2013(4):51-60.
[6]刘华春,候向宁,杨忠. 基于改进K均值算法的入侵检测系统设计[J]. 计算机技术与发展,2016(1):101-105.
[7]ZHANG S, ZHANG S, JIN Z, et al. A novel SVM by combining kernel principal component analysis and improved chaotic particle swarm optimization for intrusion detection[J]. Soft Computing,2015,19(5):1187-1199.
[8]华辉有,陈启买,刘海,等. 一种融合Kmeans和KNN的网络入侵检测算法[J]. 计算机科学, 2016, 43(3):158-162.
[9]王倩. 基于数据挖掘的入侵检测技术的研究与实现[D]. 北京:北京邮电大学,2017.
[10]郭春. 基于数据挖掘的网络入侵检测关键技术研究[D]. 北京:北京邮电大学, 2014.
[11]JOKAR P,LEUNG V. Intrusion detection and prevention for ZigBee-based home area networks in smart grids[J]. IEEE Transactions on Smart Grid,2016, (99):1-1.
[12]赵石真. 基于SVM的k-means聚类算法在WSN入侵检测中的应用[D]. 成都:西华大学,2016.
[13]BUCZAK A, GUVEN E. A survey of data mining and machine learning methods for cyber security intrusion detection[J]. IEEE Communication Survey and Tutorials, 2017(18): 1153-1176.
[14]ARIAFAR E,KIANI R. Intrusion detection system using an optimized framework based on data mining techniques[C]. Proceedings IEEE International Conference on Knowledge-Based Engineering and Innovation,2017:785-791.
[15]PENG K, LEUNG V C M, HUANG Q. Clustering approach based on mini batch kmeans for intrusion detection system over big data[J]. IEEE Access, 2018(6):11897-11906.
[16]SCULLEY D.Web-scale K-means clustering[C]. Proceedings 19th International Conference on World Wide Web,2010: 1177-1178.
[17]MOHAMMED J ZAKI, WAGNER MEIRA JR. 数据挖掘与分析:概念与算法[M]. 北京:人民邮电出版社,2017:445-474.
[18]张晓峰. 基于聚类和支持向量机的入侵检测方法研究[D]. 兰州:兰州理工大学,2018.
[19]TAVALLAEE M, BAGHERI E, LU W, et al. A detailed analysis of the KDD CUP 99 data set[C]. IEEE International Conference on Computational Intelligence for Security and Defense Applications, 2009:53-58.
[20]張新有,曾华燊,贾磊. 入侵检测数据集KDD CUP99研究[J]. 计算机工程与设计,2010,31(22):4809-4812.
[21]ENGEN V,VINCENT J,PHALP K. Exploring discrepancies in findings obtained with the KDD Cup '99 data set[J]. Intelligent Data Analysis, 2011,15(2):251-276.
(责任编辑:孙 娟)
收稿日期:2019-05-30
基金项目:浙江省自然科学基金项目(LY19F020039);之江实验室重大科研项目(2019DH0ZX01)
作者简介:欧阳潇琴(1993-),女,杭州电子科技大学通信工程学院硕士研究生,研究方向为传感器网络安全、计算机网络安全;王秋华(1978-),女,杭州电子科技大学网络空间安全学院副教授,研究方向为传感器网络安全、计算机网络安全、安全密钥管理。

