基于Prophet-LSTM模型的PM2.5浓度预测研究
王晓飞 王波 陆玉玉 张胜彬

摘 要:作为衡量空气质量的重要指标,准确预测PM2.5浓度变化尤为重要。提出Prophet和长短期记忆(LSTM)相结合的组合预测模型(Prophet-LSTM)。在模型构建过程中,首先利用Prophet模型的可分解方法,将PM2.5日值浓度序列分解成趋势、周期和随机波动分量;然后对趋势和周期分量建立Prophet模型,对随机波动分量建立LSTM模型;最后将各分量的预测值集成得到PM2.5浓度的预测值。以郑州市PM2.5日值浓度数据为例进行实证分析,结果表明,该组合预测模型相较对比模型能够更好地预测PM2.5日值浓度的变化趋势。
关键词:PM2.5浓度预测;Prophet模型;LSTM神经网络;可分解方法
DOI:10. 11907/rjdk. 191613
中图分类号:TP319 文献标识码:A 文章编号:1672-7800(2020)003-0133-04
Research of PM2.5 Concentration Forecasting Based on Prophet-LSTM Model
WANG Xiao-fei,WANG Bo,LU Yu-yu,ZHANG Sheng-bing
(Business School,University of Shanghai for Science and Technology,Shanghai 200093,China)
Abstract:As an important indicator of air quality, accurate prediction of PM2.5 concentration changes is particularly important. Aiming at this problem, a combined prediction model (Prophet-LSTM) combining Prophet and long-term short-term memory (LSTM) is proposed. In the process of model construction, firstly the paper uses the decomposition methods of Prophet model to decompose PM2.5 concentration into trend, period and random fluctuation components. Then the Prophet model is established for trend and period, and the LSTM model is established for random fluctuation. Finally, the forecasting values of each component was integrated to obtain the forecasting values of PM2.5 concentration. Taking the PM2.5 daily value data of Zhengzhou City as an example, the empirical analysis shows that the combined prediction model can better predict the variation trend of PM2.5 daily concentration compared with the comparison model.
Key Words: PM2.5 concentration forecasting; prophet model; LSTM neutral network; decomposition
0 引言
空氣污染不仅对人们的身体健康构成一定危害,而且会引起一系列环境问题。霾是由空气中的灰尘、硫酸、硝酸、有机碳氢化合物等粒子组成的气溶胶系统,雾霾会造成大气浑浊、视野模糊等恶劣天气[1-2]。作为空气环境中直径小于等于2.5 um的颗粒物,PM2.5是构成雾霾的主要成分,因为它体积小、易悬浮、传输距离长,因而对人体健康和大气环境影响更大[3-4]。应对雾霾天气、改善空气污染的首要任务就是控制PM2.5。
目前国内外学者主要通过机理模型和非机理模型两种方法对大气中的颗粒物浓度进行预测。机理模型需要详细的高空、地表数据,且涵盖污染物由产生到扩散的复杂物理化学过程,模型计算复杂,使用范围受限;非机理模型则通过历史数据分析污染物浓度的变化规律[5-7]。PM2.5浓度的变化具有非线性、突变性特点,是一种复杂的非线性系统。Jian等[8]通过差分自回归移动平均模型对街道范围的PM1.0浓度进行定量预测;张人禾等[9]对中国东北持续性强雾霾天气产生的气象条件进行分析;潘红玲等[10]对中国的重度雾霾情况进行时空分布特征研究,对其影响因子进行了分析;Asadollahfardi等[11]通过人工神经网络和马尔科夫链,将PM10、NO、NO2、CO、SO2作为输入,对每小时的PM2.5浓度进行仿真;Ausati等[12]评估自适应模型神经网络推理系统、主成分回归、多元线性回归、整体经验模态分解和广义回归神经网络混合模型用于PM2.5预测时的性能分析;余辉等[13]通过ARMAX模型对单位小时内PM2.5浓度进行预测研究。大部分学者研究侧重于宏观影响因素,多是探究气象数据、地理位置、经济等因素对PM2.5浓度变化的影响。
本文不考虑气象数据、地理位置、经济等宏观指标对PM2.5浓度变化的影响,仅研究PM2.5浓度的时序变化规律。首先利用Prophet模型的可分解方法,将PM2.5浓度分解成模型更好识别的趋势、周期和随机波动分量;在此基础上,利用Prophet模型和LSTM模型对趋势、周期和随机波动分量进行预测;最后将所有分量的预测值集成,得到PM2.5浓度的最终预测结果。
1 Prophet模型
Prophet是2017年Facebook发布的时序模型,它主要研究时序数据特征和时序变化规律,并对未来走势进行预测[14-15]。该模型不仅能够弥补传统时序模型对时序数据过于局限、缺失值需要填充、模型缺乏灵活性等不足,而且相较传统的时序模型,在模型准确率以及使用者之间的互动方面具有更好效果[16-17]。它以更简单、灵活的预测方式以及能够获得较好预测结果的特点引起人们广泛关注。Prophet的核心是分析周期性、趋势性、节假日效应等各种时间序列特征。在趋势方面,它支持加入突变点,实现分段线性拟合;在周期方面,它使用傅里叶级数建立周期模型;在节假日和突发事件方面,用户可以通过表的方式指定节假日及其前后相关天数。Prophet是一种针对时序的有效集成解决方案。
Prophet模型构成如下:
其中,[g(t)]是趋势函数,用来分析时间序列中的非周期性变化;[s(t)]代表周期性变化,例如一年或一周;[h(t)]代表节假日等偶然一天或几天造成的影响,[∈]为随机波动,代表模型没有考虑到的误差影响。
(1)趋势项:Prophet模型中的趋势增长类似于种族增长。Facebook采用改进的logistic增长模型,其中饱和值随时间动态变化,而且增长率也随着新产品等因素发生变化。
其中,C是随时间变化的饱和值(承载能力),[k+a(t)Tδ]是随时间变化的增长率,[(m+a(t)T)γ]是相应的偏置参数,[sj]是若干个转折点,[δ]是转折点处增长率的变化量。
(2)周期项:Prophet模型依靠傅里叶级数构造灵活的周期性模型,基本形式如下:
其中,P是时间序列的周期长度,N代表周期数,[an]、[bn]是需要估计的参数。
Prophet模型与其它时序模型相比主要优点如下:①灵活性:能够很容易地调整周期性,并且让用户对趋势进行不同的假设;②测量值不需要规则地间隔,也不需要对缺失值进行插值;③拟合速度快;④预测模型具有更加容易理解的参数,能够让分析者针对不同情况进行改进。
2 LSTM模型
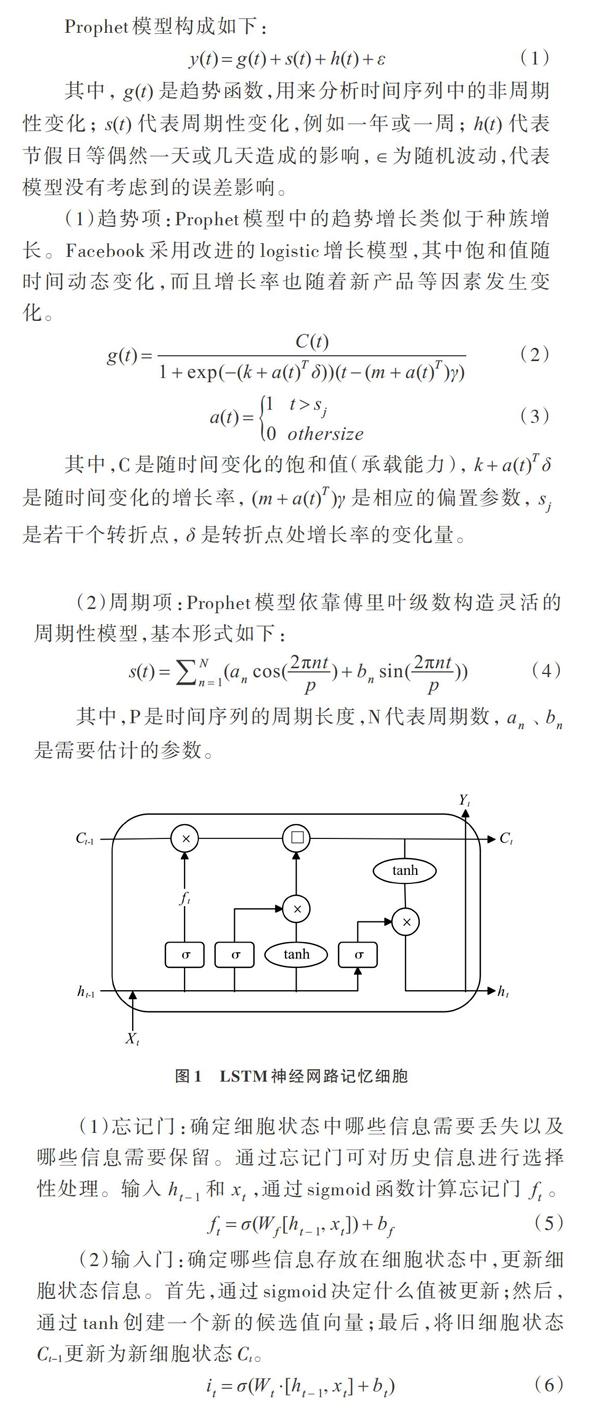
LSTM(Long Short-Term Memory)即長短期记忆网络,是对传统RNN循环神经网络模型的一种改进。将LSTM长短期记忆网络的基本链式结构展开,发现LSTM具有和RNN相似的链式结构,该链式结构解释了RNN本质上是序列相关的。目前RNN已经在自然语言处理、图像处理、语音识别等方面取得显著效果。然而,RNN在实际应用中经常面临着梯度消失问题[18-19]。Hochreiter等[20]提出的LSTM是一种RNN特殊类型,通过更为精细的信息传递机制,解决RNN所面临的梯度消失问题。LSTM模型在RNN的神经元部分增加了一个非常有用的忘记门,使得LSTM模型非常适合处理长期依赖问题。LSTM模型结构如图1所示。
LSTM通过输入门、输出门、忘记门保护和控制细胞状态。输入门控制输入记忆单元强度,输出门控制输出记忆单元强度,忘记门控制记忆单元维持旧细胞状态强度。各状态门作用如下:
(1)忘记门:确定细胞状态中哪些信息需要丢失以及哪些信息需要保留。通过忘记门可对历史信息进行选择性处理。输入[ht-1]和[xt],通过sigmoid函数计算忘记门[ft]。
(2)输入门:确定哪些信息存放在细胞状态中,更新细胞状态信息。首先,通过sigmoid决定什么值被更新;然后,通过tanh创建一个新的候选值向量;最后,将旧细胞状态Ct-1更新为新细胞状态Ct。
(3)输出门:确定输出什么信息。首先通过sigmoid确定将要输出的信息(状态值为1表示需要输出,0表示不需要输出),然后与经过tanh处理过的细胞状态相乘,最终仅仅输出需要输出的信息。
在式(5)-式(9)中,Wt、Wf、Wc、Wo表示权重向量,bt、bf、bc、bo表示偏差向量。
3 Prophet-LSTM组合模型构建
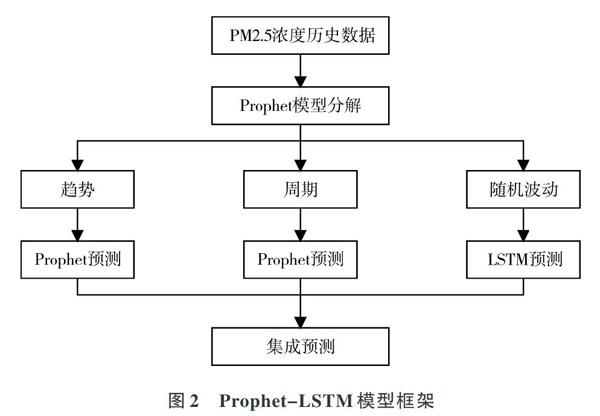
通过Prophet训练模型的可分解方法,将PM2.5浓度分解为趋势项、周期项和随机波动项,针对趋势、周期和随机波动特征分量,分别建立Prophet模型和LSTM模型进行预测;将各分量的预测值集成得到PM2.5浓度预测值。Prophet-LSTM模型预测PM2.5浓度整体框架如图2所示。
(1)首先采用Prophet模型训练的可分解方法,将PM2.5浓度序列St分解为趋势项trendt、周期项(seasonalyt,weeklyt)和随机波动项errort。
(2)将趋势项trendt和周期项(seasonalyt,weeklyt),采用Prophet模型获得第t+1天趋势预测值trendt+1和周期预测值(seasonalyt+1,weeklyt+1),针对随机波动采用LSTM模型获得第t+1天的预测值errort+1。
(3)将上述预测结果进行集成得到第t+1天PM2.5浓度的预测值St+1:
4 实证分析
本文以郑州市PM2.5日平均浓度为例检验Prophet-LSTM模型的预测能力。
4.1 数据选取与分析
本文选取2017年8月1日至2018年12月31日郑州市PM2.5日平均浓度数据进行研究,其中将2017年8月1日至2018年8月31日日平均浓度数据作为训练集,2018年9月1日至2018年9月30日的数据作为测试集。同时,为了验证模型的泛化能力,进一步选取2017年8月1日至2018年11月30日日平均数据作为训练集,2018年12月1日至2018年12月31日数据作为测试集。图3和图4是采用Prophet-LSTM组合模型对两组PM2.5时序的预测结果。
对PM2.5浓度序列进行统计分析,结果如表1所示。由表1可以看出,第一组时序数据(20170801-20180930)的偏度为2.898 0,峰度为10.595 3;第二组时序数据(20170801-20181231)的偏度为2.420 2,峰度为7.257 1,这表明PM2.5浓度序列不服从正太分布。从ADF检验结果(0.270 2,0.147 3>-2.976 4)可以看出,PM2.5濃度序列是一个非平稳序列。因此,ARMA、SVR等传统时序模型不能很好地预测PM2.5浓度,本文采用Prophet-LSTM组合模型对未来PM2.5浓度进行预测。
4.2 PM2.5日浓度预测
为验证本文提出的Prophet-LSTM模型有效性,分别采用平均绝对百分比误差(MAPE)和均方根误差(RMSE)指标作为评价指标,每个指标计算公式如下:
其中,Ft和Tt分别表示PM2.5浓度的预测值和真实值,n为样本点总个数。通过上述公式可以看出,MAPE和RMSE越小说明模型预测能力越好。
本文选取ARIMA、Prophet和LSTM模型作为比较基准,分别对两组不同月份PM2.5日浓度进行预测评估,各个模型对比结果如表2所示。
从表2可以看出,本文提出的Prophet-LSTM模型相较对比模型具有更好的预测能力,特别是对于空气污染严重的天气优势更加明显。通过对不同时间段的预测分析,该模型对样本选择的随机性具有较强的适应能力,而且该模型只考虑PM2.5时序数据的特征和规律,因此可以不考虑地域因素进行推广。
5 结语
PM2.5浓度变化是多种因素相互作用的结果。针对PM2.5浓度时序的变化规律和特征,本文提出基于Prophet模型和LSTM神经网络的组合预测模型。该模型利用Prophet模型的可分解方法对PM2.5浓度进行趋势、周期和随机误差项分解;在此基础上,针对各特征分量采用Prophet模型和LSTM相结合的方法进行预测;最后对郑州市不同月份的PM2.5浓度进行预测验证。实验结果表明,基于Prophet模型和LSTM神经网络的组合预测模型预测效果良好,可以为污染预警、空气质量评价以及环境治理提供一定的技术参考。在PM2.5预测方面,还应综合考虑气象数据、排放源、环保政策等因素,后续工作将考虑机理模型和非机理模型相结合方法,探索更加准确、适应范围更广的预测模型。
参考文献:
[1]潘慧峰,王鑫,张书宇. 雾霾污染的持续性及空间溢出效应分析——来自京津冀地区的证据[J]. 中国软科学,2015(12):134-143.
[2]张恒德,吕梦瑶,张碧辉,等. 2014年2月下旬京津冀持续重污染过程的静稳天气及传输条件分析[J]. 环境科学学报,2016(12):4340-4351.
[3]尉鹏, 任阵海, 王文杰,等. 2014年10月中国东部持续重污染天气成因分析[J]. 环境科学研究, 2015, 28(5):676-683.
[4]BRANGAN S. Development of smog-cro readability formula for healthcare communication and patient education[J]. Collegium Antropologicum, 2015, 39(1):11-20.
[5]张艺耀,苗冠鸿, 闫剑诗,等. 影响PM2.5因素的多元统计分析与预测[J]. 资源节约与环保, 2013(11):135-136.
[6]赵晓军. 时间序列的相关性及复杂性研究[D].北京: 北京交通大学, 2015.
[7]陈海燕,刘晨晖, 孙博. 时间序列数据挖掘的相似性度量综述[J]. 控制与决策, 2017, 32(1):1-11.
[8]JIAN L, ZHAO Y, ZHU Y P. An application of arima model to predict submicron particle concentrations from meteorological factors at a busy roadside in hangzhou, china[J]. Science of the Total Environment, 2012(426):336-345.
[9]张人禾, 李强, 张若楠. 2013年1月中国东部持续性强雾霾天气产生的气象条件分析[J]. 中国科学:地球科学, 2014, 44(1):27-29.
[10]潘红玲. 中国重度雾霾时空分布特征及影响因子分析[D].成都:电子科技大学, 2015.
[11]ASADOLLAHFARDI G,MADINEJAD M,ARIA S H,et al. Predicting particulate matter (pm\r, 2.5\r, ) concentrations in the air of shahr-e ray city, iran, by using an artificial neural network[J]. Environmental Quality Management, 2016, 25(4):71-83.
[12]AUSATI S,AMANOLLAHI J. Assessing the accuracy of ANFIS, EEMD-GRNN, PCR, and MLR models in predicting PM2.5[J]. Atmospheric Environment,2016(142):465-474.
[13]余辉,袁晶,于旭耀. 基于ARMAX的PM_(2.5)小时浓度跟踪预测模型[J]. 天津大学学报:自然科学与工程技术版, 2017(1):109-115.
[14]彭志行, 陶红, 贾成梅, 等. 时间序列分析在麻疹疫情预测预警中的应用研究[J]. 中国卫生统计, 2010, 27(5):459-463.
[15]刘璐, 丁福利, 孙立民. 基于SVM的烟草销售量预测[J]. 软件导刊, 2016, 15(11):134-137.
[16]TAYLOR S J,LETHAM B. Forecasting at scale[J]. The American Statistician, 2017, 72(1):100-108..
[17]李丽萍, 段桂华, 王建新. 基于Prophet框架的银行网点备付金预测方法[J]. 中南大学学报:自然科学版, 2019(1):182-186.
[18]GRAVES A. Supervised sequence labelling with recurrent neural networks[J]. Studies in Computational Intelligence, 2012(3):385-391.
[19]邸浩, 赵学军, 张自力. 基于EEMD-LSTM-Adaboost的商品价格预测[J]. 统计与决策, 2018, 34(13):105-112.
[20]HOCHREITER S,SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8):1735-1780.
(责任编辑:杜能钢)
收稿日期:2019-04-27
基金项目:国家自然科学基金项目(71572113)
作者简介:王晓飞(1994-),男,上海理工大学管理学院硕士研究生,研究方向为机器学习、数据挖掘;王波(1960-),男,博士,上海理工大学管理学院教授,研究方向为决策分析、数据挖掘;陆玉玉(1994-),女,上海理工大学管理学院硕士研究生,研究方向为决策分析、数据挖掘。本文通讯作者:王晓飞。

