基于正态检验的瓦斯涌出异常预警方法

张天宇　王红娟

摘 要：为实现瓦斯灾害智能预警，从统计学角度分析瓦斯涌出时间序列概率分布特点，提出基于正态性检验的瓦斯涌出异常预警方法，利用Matlab对时间序列进行Ryan-Joiner与偏度—峰度联合正态检验。实验结果表明，当瓦斯涌出状态变化平稳没有大幅度波动时，瓦斯涌出序列服从正态分布;当瓦斯涌出状态出现大幅度波动且变化异常时，瓦斯涌出序列不服从正态分布。利用联合正态检验方法可实现瓦斯涌出异常提前预警，为辅助瓦斯灾害防治提供理论依据。

关键词：瓦斯涌出异常;正态分布;Ryan-Joiner检验;偏度—峰度检验;联合检验;预警

DOI：10. 11907/rjdk. 192636

中图分类号：TP301   文献标识码：A                 文章编号：1672-7800（2020）003-0099-05

Gas Emission Abnormality Warning Method Based on Normality Test

ZHANG Tian-yu1，WANG Hong-jun2

（1. School of Computer Science and Engineering，Shandong University of Science and Technology，Qingdao 266590，China;

2. Department of Information Engineering，Shandong University of Science and Technology，Taian 271019，China）

Abstract： In order to realize the intelligent early warning of gas disaster， the probability distribution characteristics of gas emission time series are analyzed from the perspective of statistical principle. A gas emission abnormality warning method based on normality test is proposed. The time series is be utilized to perform Ryan-Joiner and skewness-kurtosis joint normality test by using Matlab.The experimental results show that the gas emission sequence obeys the normal distribution when the gas emission state changes smoothly and does not fluctuate greatly. When the gas emission state fluctuates greatly and the variation is abnormal， the gas emission sequence does not obey the normal distribution. This paper uses the joint normal test method to realize the advance warning of gas emission anomaly， and provides a theoretical basis for the prevention and control of gas disaster.

Key Words：gas emission abnormality;normal distribution;Ryan-Joiner test;skewness-kurtosis test;joint normality test;early warning

0 引言

我國煤矿瓦斯事故发生频率较高，瓦斯灾害严重威胁人民生命财产安全，瓦斯灾害预测预是煤矿生产亟待解决的难题[1-3]。瓦斯灾害预测预警可在灾害发生前进行预报，从而使相关人员及时采取合理措施，达到预防灾害发生的目的[4-5]。目前，针对瓦斯灾害预测预警的研究已取得丰硕成果。如赵艳芹等[6]提出一种基于 Eclat 算法的瓦斯安全预测模型，采用垂直数据库数据存储结构，每条记录按项目-数据集的格式存储，对矿井下多指标监测数据进行数据挖掘，获得影响指标相互之间隐含关系，预测井下异常事件发生概率;屈世甲[7]对工作面煤与瓦斯突出危险性及瓦斯涌出特征值之间的相关性进行了分析研究，通过提取瓦斯涌出量平均值、最大值及落煤瓦斯浓度数据斜率，将其作为瓦斯涌出特征值，结合煤与瓦斯突出危险性指标，提出了工作面煤与瓦斯突出危险性及瓦斯涌出特征值回归分析方法;郭得勇等[8]基于层次分析法（Analytic Hierarchy Process，AHP）与可拓学理论，利用 Visual Basic和 ArcEngine 组件，设计以数据采集模块、查询模块和预警模块组成的突出预警系统，开发客户端软件系统，结合矿井基础参数及工作面煤与瓦斯突出预测指标，构建煤与瓦斯突出预警体系。此外，还有学者提出了基于时间序列[9-12]、数据挖掘[13]、灰色理论[14-15]、神经网络[16-21]的瓦斯灾害预测预警方法。以上瓦斯涌出预测预警方法虽然为瓦斯灾害防治提供了重要的参考依据，但需依赖井下静态测量参数，无法实现动态化预警。

本文基于煤矿实时监测系统的瓦斯涌出时间序列，从统计学角度分析瓦斯涌出时间序列概率分布特点，对瓦斯涌出时间序列进行特征挖掘，提出基于正态性联合检验的瓦斯涌出异常预警方法。将瓦斯涌出时间序列是否符合正态分布作为预测预警依据，利用正态性检验原理动态辨别瓦斯涌出异常状态，可大幅提升瓦斯涌出异常预警的准确性。传统正态性检验方法在适用方向、计算效果等方面存在一定差异，且单一正态性检验方法存在一定预警缺陷，本文提出的Ryan-Joiner与偏度—峰度联合正态检验方法，可在瓦斯涌出异常时期实时动态地发出预警信号，为辅助瓦斯灾害的防治提供理论依据。

1 正态检验原理

煤矿生产过程中，突现的瓦斯异常涌出是由于多方因素的影响。当地质构造发生明显变化时，煤体结构会有明显的不均衡性;煤层顶板大面积垮落时，采空区及邻近煤层瓦斯涌向回采区;不均匀的地应力致使煤层中瓦斯压力较高，成为瓦斯异常涌出诱因;不同的采掘技术对瓦斯涌出的影响程度有差异性。

正态分布又名高斯分布[22-23]，是概率论中最重要的一种概率分布。在科学实验中，很多隨机变量的概率分布可近似地用正态分布加以描述。如果一个随机变量是受许多微小的独立随机因素影响的结果，则可认为这个随机变量具有正态分布。正态性检验基本原理[24-26]是根据研究需要，假设研究整体H0服从正态分布，并假定H0成立。如果研究数据与理论假设之间的偏离程度达到“显著”则拒绝H0，根据研究问题指定偏离显著程度为一个正数α。当H0正确时，它被拒绝的概率小于α，α此时称为显著性水平。在瓦斯涌出稳定正常、影响瓦斯涌出的因素变动比较均匀时，此时瓦斯浓度实测值可被视为随机变量，时间序列服从正态分布;而在瓦斯涌出异常、瓦斯涌出的影响因素发生显著波动时，此时瓦斯时间序列不服从正态分布。因此，随着瓦斯监测数据的不断更新与瓦斯涌出时间序列动态变化，可根据联合正态检验方法实时判断当前瓦斯涌出状态。

2 时间序列预处理

2.1 数据预处理

在监测数据采集与传输过程中经常遇到3种失真情况：①由于现场施工或其它原因造成传感器断电，导致数据缺失或瓦斯浓度数据突然从正常变为零值;②监测数据在传输过程中由于干扰因素造成“冒大数”现象，瓦斯浓度数据出现突变后又迅速回归正常;③进行传感器标校试验时，瓦斯浓度会在短时间内从正常值到异常值，随后慢慢恢复正常。所以监控系统数据十分重要，特别是进行瓦斯浓度数据二次使用与数据挖掘时，必须预先对监测数据进行处理。

由于煤矿井下环境条件恶劣，矿井监控系统各监测部件受到灰尘、水蒸汽和温度等多因素干扰，还可能遇到传感器及分站电源、存储介质及网络传输、电磁干扰等方面故障，以及受到外界一些恶劣因素的影响，往往存在数据缺失、数据异常等错误情况，所以需对采集数据预先进行处理[27]。常用的瓦斯监测数据处理方法有：移动平均线补偿法、AR模型补偿法、时间序列平滑移动法。根据不同的数据异常情况，选用不同的监测数据处理方法，本文采用移动平均线补偿法对采集数据进行预处理。由瓦斯监测数据得到的瓦斯浓度时间序列{Xs，s=1，2，……}，在时间序列中某时刻t=a时，突然出现零值或突现跃变瓦斯浓度值且数目较少时，一般而言间隔小于 5 min，应计算瓦斯浓度序列的移动平均线xa进行数据补偿。其补偿浓度值通过计算在t=a时刻前 Rx个数据点（一般取时间长度 20 min）的均值替代。

2.2 时间序列划分

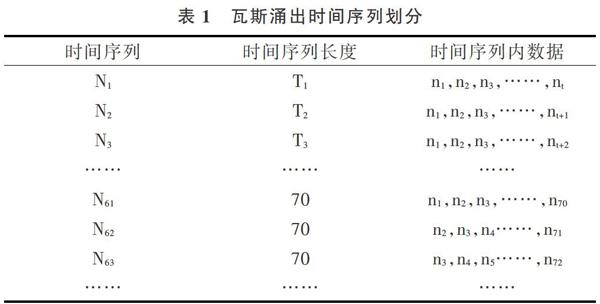
随着煤矿瓦斯监控系统瓦斯监测数据的更新，从中获取时间段内经过数据预处理的瓦斯涌出时间序列，由当前时刻t向前推进9个采样时刻得到初始序列N1，区间[t-9，t]内为N1包含的数据，则初始时间序列长度为T1。对瓦斯涌出序列进行动态划分，生成时间序列N1，N2，……，Ns。

其中：nt为t时刻瓦斯浓度值，t为采样时刻。

时间序列长度T依次为T1，T2，……，Tt （10≤T≤70），时间序列划分信息如表1所示。

3 瓦斯涌出时间序列联合正态性检验

3.1 Ryan-Joiner检验

数据整体服从正态分布，样本均值和方差则相互独立。 一般需先假设数据或参数分布形态服从正态分布，之后利用检验统计量判断数据整体是否符合正态分布，该统计检验假设是样本来自于一个正态母体。 因此，一方面，若p值小于选择的显著性水平（α值通常为0.05），则在更大概率下应拒绝原假设，样本数据不是来自一个正态分布母体;另一方面，若p值比选择的显著性水平α大，则没有理由拒绝原假设，样本数据来自于一个正态分布母体。

Ryan-Joiner检验是目前序列正态性检验效果较好的方法之一，可验证一个随机样本数据是否来自正态分布。由序列数据可判断序列是否符合正态分布，对划分得到的各个瓦斯涌出时间序列Ns以1～α的置信水平进行Ryan-Joiner正态检验，利用Ryan-Joiner检验原假设H0之前，需先将各序列中样本数据按照从小到大的顺序排列，再依次计算时间序列检验统计量R，如式（3）所示。

其中，[pi=i-3/8n+1/4]，i=1，2，……，n;[bi=Φ-1（pi）]，i=1，2，……，n;n为序列中数据个数。

以1～α为置信水平的检验法则：当检验统计量与检验分位数的关系为R

其中，n为序列长度，即序列中数据个数。

3.2 偏度—峰度检验

频数分布有正态分布和偏态分布之分。正态分布指多数频数集中在中央位置，两端频数分布大致对称;偏态分布指频数分布不对称，集中位置偏向一侧。若集中位置偏向数值小的一侧，称为正偏态分布;集中位置偏向数值大的一侧，称为负偏态分布。如果频数分布的高峰向左偏移，长尾向右侧延伸称为正偏态分布，也称右偏态分布;同样地，如果频数分布的高峰向右偏移，长尾向左延伸则成为负偏态分布，也称左偏态分布。

偏度系数是描述数据分布形态的统计量，反映总体取值分布对称性，偏度绝对值越大，其分布形态偏斜程度越大;峰度系数是描述总体中所有取值分布形态陡缓程度的统计量，峰度绝对值越大，其分布形态陡缓程度与正态分布的差异程度越大。对于序列中的数据，假如随机变量符合正态分布，则偏度系数及峰度系数也符合正态分布。序列分布的数学期望为0，均方差[sg1]与[sg2]为：

其中，n为序列长度，即序列中数据个数。

对于不同时刻生成的瓦斯涌出时间序列，偏度系数g1与峰度系数g2为：

其中，x为时间序列均值，[x=1ni=1nxi];s为时间序列标准差，[s=1ni=1n（xi-x）2];n为序列中数据个数。

对瓦斯涌出时间序列作正态性检验：假设随机变量遵从正态分布，在显著水平α=0.05下，当且仅当[g11.96sg1]且[g21.96sg2]时，接受假设，认为随机变量服从正态分布，即瓦斯涌出时间序列服从正态分布的特征;否则，拒绝假设，认为随机变量不服從正态分布[29]，瓦斯涌出时间序列不服从正态分布特征。

4 瓦斯涌出异常预警方法流程

利用连接数据服务器、数据管理系统及矿井安全监控系统获取的数据，利用本文预警方法对瓦斯涌出时间序列进行有效分析，根据不同时刻的时间序列对瓦斯涌出状态进行判定，输出预警结果。

5 实验与对比分析

从山西某煤矿瓦斯监测系统中截取两段工作面瓦斯涌出为异常状态前后时间内的监测数据，对瓦斯监测数据进行预处理后，生成瓦斯涌出时间序列作为分析对象，获取的工作面瓦斯涌出时间序列如图2所示。

对上述工作面瓦斯涌出时间序列进行划分，t=10min时，获得长度为T=10的瓦斯涌出初始时间序列。

不断获取瓦斯监测数据，不同时刻生成新的瓦斯涌出时间序列N2，N3，……，Ns。

随着瓦斯涌出时间序列的不断更替，判定瓦斯涌出状态，对各个时刻不同的瓦斯时间序列进行Ryan-Joiner与偏度—峰度联合正态检验，以瓦斯涌出时间序列不服从正态分布作为判断瓦斯涌出异常的依据，即当t时刻不满足R≥Rα及[g11.96sg1]且[g21.96sg2]时，认为t时刻瓦斯涌出序列不符合正态分布，此时瓦斯涌出进入异常状态，并发出预警信号以提醒需采取相应措施。

利用Matlab对该工作面不同时刻生成的瓦斯涌出时间序列进行Ryan-Joiner与偏度—峰度联合正态检验，瓦斯涌出异常检验结果如图3、图4所示。

对该工作面瓦斯涌出时间序列进行联合正态检验，挖掘该工作面瓦斯涌出时间序列分布特征，以此作为瓦斯涌出状态判断依据。由实验结果可看出，当时间序列不符合正态分布时，判定此时刻瓦斯涌出进入异常阶段，表明瓦斯涌出变化显著，发出预警信号。由图2（a）可知，第一次瓦斯涌出异常时间序列t=39min时，瓦斯浓度为0.49%，较之前时段瓦斯浓度有突然增大的趋势。由实验结果图3（a）、图4（a）可看出此时 Ryan-Joiner检验统计量R开始位于检验分位数之下，序列偏度值与峰度值不满足[g1]1.96[sg1]且[g2]1.96[sg2]的正态判定条件，此时发出报警信号，随后瓦斯涌出量发生大幅度变化，工作面状况发生改变。由图3（b）、图4（b）实验结果分析可知，第二次瓦斯涌出异常共发出三次预警信号，分别为：在t=49min时，瓦斯浓度为0.80%，瓦斯浓度突然跃变增大;在t=92min时，检验统计量R小于检验分位数且序列偏度值不满足[g2]1.96[sg2]的正态判定条件，此时刻瓦斯涌出异常;在t=101min时，序列偏度值不满足[g2]1.96[sg2]的正态判定条件，发出预警信号，瓦斯浓度在后续时段突然增大且增长幅度较大，随后R检验量一直处于检验分位数之下，并且序列偏度值与峰度值均不满足正态检验条件，表明瓦斯涌出序列不符合正态分布，瓦斯涌出状态异常。

一段时间内的瓦斯浓度均值可说明这段时间内的瓦斯涌出变化情况，均方偏差可说明瓦斯涌出波动状况。将两次异常的瓦斯涌出时间序列划分为3个时间段，每个时间段的瓦斯浓度平均值与瓦斯浓度均方偏差如表2（a）、（b）所示。

由表2（a）可知，第一次瓦斯涌出异常时间序列的第一时间段到第二时间段间，瓦斯浓度呈现上升趋势，瓦斯浓度正在逐步升高，且均方偏差反映了瓦斯浓度变动不稳定，工作面状况正在发生改变，第三时间段均值与均方偏差有下降趋势;由表2（b）可知，第二次瓦斯涌出异常时间序列的第一到第三时间段内，瓦斯浓度平均值逐步升高且均方偏差增大，说明瓦斯浓度在逐步增大且变动不稳定。上述结果与本文实验结果相吻合。通过对工作面瓦斯涌出时间序列分布特征的检验分析，得出当瓦斯涌出状态平稳且没有大幅度波动时，瓦斯涌出序列服从正态分布;而当瓦斯涌出状态发生显著变化时，瓦斯涌出序列不服从正态分布。将序列分布特征作为涌出状态判定依据，在瓦斯涌出异常时刻发出预警信号，表示工作面发生显著变化且瓦斯涌出进入异常阶段。

6 结语

本文从统计学角度分析瓦斯涌出时间序列概率分布特点，在瓦斯涌出稳定正常的时期，影响瓦斯涌出的因素变动比较均匀，此时瓦斯浓度实测值可被视为随机变量，时间序列服从正态分布;而在瓦斯涌出异常时期，瓦斯涌出的影响因素发生显著波动，此时瓦斯时间序列不服从正态分布。本文根据该特征获取瓦斯涌出时间序列并进行区间划分，提出了基于正态性检验的瓦斯涌出异常预警方法，利用Matlab对不同时刻的瓦斯涌出时间序列进行实时Ryan-Joiner与偏度—峰度联合正态检验。对由监测数据得到的工作面瓦斯涌出时间序列进行正态分布特征检验，可在瓦斯涌出异常关键时期发出预警信号，为瓦斯灾害预测预警提供参考依据。

参考文献：

[1]于不凡，王佑安. 煤矿瓦斯灾害防治及利用技术手册[M]. 北京：煤炭工业出版社，2005.

[2]张铁岗. 矿井瓦斯综合治理技术[M]. 北京：煤炭工业出版社，2001.

[3]宁德义. 我国煤矿瓦斯防治技术的研究进展及发展方向[J]. 煤矿安全，2016，47（2） ：161-165.

[4]文光才，宁小亮，赵旭生. 矿井煤与瓦斯突出预警技术及其应用[J]. 煤炭科学技术，2011，39（2）：55-58.

[5]赵旭生，宁小亮，张庆华，等. 煤与瓦斯突出预警方法探讨[J]. 工矿自动化，2018，44（1）：6-10.

[6]赵艳芹，张恒，童朝娣. 瓦斯灾害预警模型的Eclat算法[J]. 黑龙江科技大学学报，2019，29（4）：515-520 .

[7]屈世甲. 矿井工作面突出危险性与瓦斯涌出特征回归分析的研究[J]. 工矿自动化，2015，41（5）：74-77.

[8]郭德勇，胡杰，王彦凯. 煤与瓦斯突出层次—可拓预警技术及应用[J]. 中国安全科学学报，2017，27（1）：88-92.

[9]张宝燕，李茹，穆文瑜. 基于混沌时间序列的瓦斯浓度预测研究[J]. 计算机工程与应用，2011，47（10）：244-248.

[10]吴海波，施式亮，念其锋. 基于Spark Streaming流回归的煤矿瓦斯浓度实时预测[J]. 中国安全生产科学技术，2017，13（5）：84-89.

[11]董丁稳. 基于安全监控系统实测数据的瓦斯浓度预测预警研究[D]. 西安：西安科技大学，2012.

[12]单亚锋，侯福营，付华，等. 基于改进极端学习机的混沌时间序列瓦斯涌出量预测[J]. 中国安全科学学报，2012，22（ 12）：58-63.

[13]程建，白静宜，钱建生，等. 基于混沌时间序列的煤矿瓦斯浓度短期预测[J]. 中国矿业大学学报，2008，37（2）：231-235.

[14]刘翔，杨帆. 基于数据挖掘技术的瓦斯灾害信息特征提取[J]. 煤炭技术，2016，35（8）：130-132.

[15]郝天轩，李鹏飞. 基于灰色关联分析-GA-BP 模型预测煤层瓦斯含量[J]. 中国矿业，2016 （ 11）：116-120.

[16]郭德勇，李念友，裴大文，等. 煤与瓦斯突出预测灰色理论-神经网络方法[J]. 北京科技大学学报，2007，29（4）：354-357.

[17]朱志洁，张宏伟，韩军，等. 基于 PCA-BP 神经网络的煤与瓦斯突出预测研究[J]. 中国安全科学学报，2013，23（4）：45-50.

[18]陈志华. 基于Hadoop的神经网络算法在网络学习评价中的应用研究[J]. 计算机与数字工程，2016，44（2）：248-251.

[19]张海军. 基于云计算的神经网络并行实现及其学习方法研究[D]. 广州：华南理工大学，2015.

[20]曹博，白刚，李辉. 基于 PCA-GA-BP 神经网络的瓦斯含量预测分析[J]. 中国安全生产科学技术，2015，11（5）：84-90.

[21]刘奕君，赵强，郝文利. 基于遗传算法优化 BP 神经网络的瓦斯浓度预测研究[J]. 矿业安全与环保，2015，42（2）：56-60.

[22]ANDERSON T W，DARLING D A. Asymptotic theory of certain goodness of fit criteria based on stochastic processes[J].  Annals of Mathematical Statistics，1952（23）：193-212.

[23]STEPHENS M A.EDF statistics for goodness of fit and some comparisons[J]. Journal of The American Statistical Association，1974，347（69）：730-737.

[24]COLES S G. On goodness-of-fit tests for the two-parameter Weibull distribution derived from the stabilized probability plot [J]. Biometrika ， 1989，76（3）：593.

[25]WANG X L，WEN Q H，WU Y H. Penalized maximal test for detecting undocumented mean change in climate data series[J].  Journal of Applied Meteorology and Climatology，2007，46（ 6）：916-931.

[26]章刚勇，阮陆宁. 基于Monte Carlo 随机模拟的几种正态性检验方法的比较[J].  统计与决策，2011，7：17-20.

[27]李文顺. 监控系统瓦斯浓度数据预处理方法的探讨[J]. 能源技术与管理，2014，39（3）：23-26.

[28]RYAN T， JOINER B.Normal probability plots and tests for normality[EB/OL]. http：//scholar.google.com/scholar？hl=en&btnG=Search& q=intitle：Normal+probability+plots+and+tests+for+normality#0.

[29]吉曹翔，李崇，陈鹏心，等. 沈阳市降水量正态分布检验及其时空变化特征[J]. 干旱气象，2018，36（6），954-962.

（责任编辑：江 艳）

收稿日期：2019-12-20

基金项目：国家重点研发计划项目（2017YFC0804406）;山东省重点研发计划项目（2016ZDJS02A05）;泰安市科技发展计划项目（2018GX0007）

作者简介：张天宇（1995-），女，山东科技大学计算机科学与工程学院硕士研究生，研究方向为瓦斯涌出预测预警;王红娟（1974-），女，博士，山東科技大学信息工程系副教授，研究方向为三维建模算法及瓦斯涌水量计算。