改进遗传—蚁群算法求解多维0/1背包问题
余典 吴勇 余山


摘 要:针对传统启发式算法难以平衡求解收敛次数与求解精度问题,通过充分分析GA和ACO两种算法的优缺点,设计了一种改进的遗传蚁群算法。将算法分为上下两步,分别以GA和ACO为主。在GA中引入信息素更新机制连接上下两部分算法;在ACO中引入遗传变异操作尽可能扩大解的范围。同时结合两种算法各自解的继承方式,采用合适的方法分别处理这两部分产生的不可行解。获得解后,通过引入交换邻域的爬山法思想进一步尝试优化解。最终在保证求解精度的前提下,减少求解所需的迭代次数。实验结果表明,在需要保证求解精度的前提下,相比传统GA,该方法的求解效率提高了一个量级。
关键词:0/1多维背包;遗传蚁群混合算法;交换邻域爬山算法
DOI:10. 11907/rjdk. 191598
中图分类号:TP301 文献标识码:A 文章编号:1672-7800(2020)003-0087-04
Modified Genetic Ant Colony Hybrid Algorithm for Solving
Multidimensional 0-1 Knapsack Problem
YU Dian1,WU Yong2,YU Shan2
(1. China Academy of Telecommunication Technology,Beijing 100083,China;
2. Semiconductor Manufacturing International Corporation (Beijing),Beijing 100176,China)
Abstract:Aiming at the problem that traditional heuristic algorithm is difficult to balance the solution of convergence times and solution precision, we design an modified genetic and ant colony hybrid algorithm by analyzing the advantages and disadvantages between GA and ACO algorithms. The algorithm is divided into two steps which are based on GA and ACO respectively. The pheromone update method is introduced in the step based on GA to connect with the next step. Meanwhile, mutation operation and crossover operation are introduced in the step based on ACO for getting more solutions. Besides, the appropriate method is used to deal with the infeasible solutions generated in these two steps. Finally, in order to optimize the solution further, hill-climbing algorithm of exchange neighborhood search is introduced after the solution is obtained. Finally, under the premise of ensuring the accuracy of the solution, the number of iterations required for the solution is shortened. The experimental results show that the efficiency of the proposed method is increased by an order of magnitude compared with the traditional GA under the premise of ensuring the accuracy of the solution.
Key Words:multidimensional knapsack problem; genetic ant colony hybrid algorithm; hill-climbing algorithm of exchange neighborhood search
0 引言
多維背包问题(Multidimensional Knapsack Problem, MKP)是著名的整数规划问题之一,属于NP-hard问题[1]。它的实际应用场景很多,如工厂中的资源分配形式、数据加密、投资组合、机台调度等。近几十年研究出各种各样的解决方法,其中精确算法有分支限界法、动态规划法等,近似算法有贪婪方法、蚁群算法等[2]。近几年对该问题的研究主要集中于以遗传、蚁群算法为代表的元启发式算法[3]。
遗传算法[4](Genetic Algorithm,GA)由美国学者Holand于1975年首先提出,是一种模拟达尔文遗传选择和自然淘汰的生物进化论计算模型。它通过模拟自然界的遗传、变异以及适者生存进化机制获取所求问题的解。这种算法优点是简单、通用、鲁棒性强,适用并行分布处理,应用范围广。它是一种随机的、以交叉操作为核心的全局多点搜索算法,在运算前期能很快达到最优解的90%左右[5]。但是在之后,由于交叉编译操作获得的解会大量重复于之前获得的解集,导致要花费很长时间才能对解的质量作进一步优化。蚁群算法(Ant Colony Optimization,ACO)是Dorigo[6]于1991年提出的一种基于蚂蚁种群的新型优化算法,使用单纯的蚁群算法求解背包问题主要通过不断重复放置蚂蚁,依据信息素寻找一串可行的解集。更新信息素,通过信息素的不断积累逐渐收敛到最优解。由于ACO算法中,前面的解通过更新信息素的方式能对后面的解产生正反馈,因此使ACO的收敛速度加快,避免了类似GA后期大量的重复搜索过程。但是ACO存在以下几个问题:①前期信息素浓度较低且分布平均时,整体算法收敛较慢;②算法容易出现停滞现象,也就是当搜索到一定程度后,少数几个节点上积累的信息素浓度足够大,使得寻找到的解都集中在这几个节点上,不能对解空间进一步搜索,最终导致算法过早收敛在一个较优的解上。
MKP发展至今,相关问题有多种不同的表现形式,王熙照、贺毅朝[7]对此作了比较系统的归纳。0/1背包问题是其中最基本的背包问题,一直以来都有不少学者对其进行研究。
近年来,对类似MKP这种NP-hard类型问题的求解方法主要分为两类:①寻找新的启发式算法求解此类问题,如刘雪静、贺毅朝[8]等采用细菌觅食算法求解0/1背包问题。这种算法具有局部搜索、并行搜索能力强等优点,但这种算法在每轮循环中需要经过趋化、迁移和复制3个步骤,而其中趋化又包含翻转和游动等,会造成算法需要调整的变量数量多、不易控制等问题。高思奇、邢玉轩等[9]提出通过改进蛙跳算法求解背包问题,这种算法具有比较好的求解效率,但就原始蛙跳算法而言,算法容易收敛到局部最优解。此外,近几年出现了人工鱼群算法(AFSA)[10]和声搜索算法(HS)[11]、萤火虫算法[12]、二进制蝙蝠算法(BBA)[13]等研究热点;②通过优化或混合原有算法求解问题。如赵学武, 刘向娇等提出一种改进的遗传算法求解背包问题。这种改进算法通过每轮获得的解集适应值,自动调整变异概率。通过算法调整,保证每次装入的物体单位质量价值大以加快算法收敛速度。这种改进算法减少了收敛到最终结果的迭代轮次,加快了算法的收敛速度,但是牺牲了解的多样性,且没有很好地解决后期无用搜索量大的问题。罗星星等在原有遗传算法基础上引入了3种新的变异方式:散播变异、移位变异和插入变异,丰富了解的种类,但并没有很好地解决在算法后期收敛慢的问题。刘梦佳和王娜等在主要思路上都采用了遗传蚁群混合算法,通过每轮迭代将解集分为两类:一类适应度较高的用于遗传算法,其余的用于蚁群算法,混合解集按照适应度获取下一阶段的解集,这种混合算法能获得优于普通GA的收敛速度和优于普通ACO的寻解范围。但是每轮用于蚁群算法的那些解都是重新构建的,实际上浪费了计算资源。另外,由于设定用于GA的解数量是固定的,因而这种算法会有类似于普通GA或普通ACO的缺陷。除此之外,刘梦佳等通过综合遗传算法和模拟退火算法,提出了改进的Memetic算法用于求解多维0/1背包问题。
无论是新的元启发式算法还是在现有算法基础上进行改进,都是为了更快地寻找到更优的解。
针对传统启发式算法难以平衡求解收敛次数与求解精度问题,本文通过分析GA和ACO两种算法之间的优缺点,设计了一种改进的遗传蚁群算法,将整个算法分为上下两步,分别以GA和ACO为主。在GA中引入信息素更新机制连接上下两部分算法;在ACO中引入遗传变异操作尽可能地扩大解的范围,同时采用合适的方法处理这两部分中产生的不可行解。在最后获得解后,通过引入爬山法思想进一步尝试优化解,最终在保证求解精度的前提下减少求解所需的迭代次数。实验结果表明,在保证求解精度的前提下,相比传统GA,该方法的求解效率提高了一个量级。
1 0/1多维背包问题数学模型
一般将0/1MKP问题构建数学模型如下:
其中:[Np]表示背包数目,No表示物体数目,Pi(i=1,2,…Np)表示物体i的价格,Cj(j=1,2…Np)表示每个背包的最大资源量,Wij(i=1,2,…No, j=1,2…Np)表示每个物体i对背包j的资源占用。
2 改进的混合遗传蚁群算法
2.1 算法设计思想
(1)考虑到遗传算法在运行前期求解效率高,而且比蚁群算法更容易生成一组解,所以在混合算法前期采用遗传算法以快速獲得较优解;同时由于蚁群算法的解集生成并不直接依赖于上一组解的解值,而是前面积累的信息素,所以在遗传算法中引入信息素更新机制,让遗传算法的解能影响到后面蚁群算法求解,加快算法收敛速度。
(2)蚁群算法在信息素浓度高时,由于正反馈效应及收敛速度快的特点,可在后期采用蚁群算法加快收敛速度。为防止最后收敛到局部最优解,引入变异交叉操作增大寻解范围,通过对普通遗传算法的结果分析能较容易地找到这两步的切换节点。
2.2 算法流程
步骤一:变量初始化。设置最大迭代次数N,第一步的循环次数N1,变异概率Pm ,交叉概率Pc,解集大小size,初始信息素浓度矩阵ph(Np·1),每条路线信息素更新总量Q,信息素挥发因子ρ,计算能见度矩阵Me。
步骤二:获取初始解集。通过随机生成0或1得到一组(NO·size)的矩阵Mg作为初始解集,其中的每一列就是一个初始解。
步骤三:进入算法第一步(GA为主)。①通过交叉操作获得一组交叉矩阵Mc;②通过变异操作获得一组变异矩阵Mm;③将Mg、Mc、Mm组合为新矩阵Mg;④获得Mg解集对应的价格序列Ap;⑤对Mg中超重的解集对应的价格进行惩罚;⑥对解集中满足限制条件的解,按照蚁周模型更新信息素;⑦按照轮盘赌思想得到下一组解集Mg;⑧当循环次数≤N1时,返回步骤三①。
步骤四:进入算法第二步(ACO为主):
(1)参数初始化:清空解集Mg,启发因子α,能见度因子β。
(2)将size只蚂蚁尽量分散放置在各个物体上。
(3)计算每个物体被选择的概率。
(4)依次为每只蚂蚁s生成一组解集:①设置指示标志a=0,该蚂蚁当前对资源占用的总量为Ac;②通过轮盘赌选择该蚂蚁下一个可能选择的物体b;③将b占用的资源加到Ac上,如果此时仍然满足下式:[?j=1,2,?NP,AcjCj],则设置Mc(s,b)为1(代表选上),否则设置为-1(代表不可选);④如果a≤No,就返回步骤四之(2)。
(5)对目前获得的解集Mg进行变异操作,并对不满足约束条件的解进行修正,获得Mam。
(6)对目前获得的解集Mg进行交叉操作,并对不满足约束条件的解进行修正,获得Mac。
(7)按照蚁周系统对物体上的信息素进行更新。
(8)保留当代最优解。
(9)如果迭代次数小于等于N,则转到步骤四之(2);否则输出最优解并结束程序。
步骤五:对得到的结果利用交换邻域的爬山法进行优化。
2.3 算法策略
步骤一中,计算能见度矩阵Me。这里的能见度矩阵用于在ACO算法中计算不同物体的选择概率,见步骤四之(3)。具体算法如下:
其中:ph是No×1维矩阵,表示各物体上的信息素浓度;Me是No×1维矩阵,选择概率[Pkij]表示第k只蚂蚁在物体i上选择物体j的概率。
由式(2)及MKP可知,价格越高消耗资源越少的物品更应该被选中。对于KMP,本文采用按背包容量比值进行加权的价格/占重比确定每个物体的能见度,实现公式见式(3)和式(4)。
其中:[Me(i)]表示物体i的能见度,[percj]表示背包j的占比。
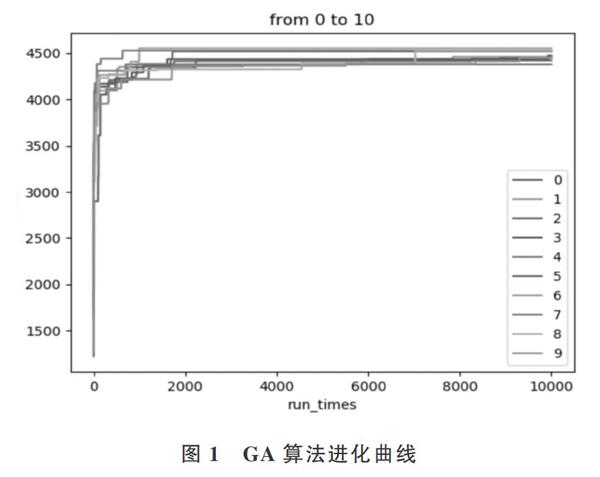
交叉操作(步骤三之①,步骤四之(6))中,循环size次,每次生成一个随机数random∈[0,1]。当random 步骤三之(5)通过将不可行(超背包容量)的解的价格设置为当前解集的最小价格对其进行惩罚。这里不采用人为修复为可行解方法,在GA中该轮解集会继承到下一轮中,如果采用修改为可行解的方法实际上会降低后续解的多样性。步骤四之(6)采用修正的方法在于ACO中当前轮的解集不能继承到下一轮,而信息素的更新只会采用可行解,所以这里采用修复方法以增加求解速率。 本文采用依次删除不可行解中可见度最小的元素直到满足约束条件的方法对不可行解进行修复。 根据信息素更新策略不同,一般将蚁群模型分为蚁周模型(antcycle system)、蚁量系统(ant-quantity system)、蚁密系统(ant-density system),这里采用性能最好的蚁周模型。蚁周模型更新信息素方式如下: 其中,[phki(t)]代表在第t轮第k只蚂蚁寻找解时,物体i上的信息素浓度;[Δphki(t,t+1)]代表第t轮结束后蚂蚁k在物体i上更新的信息素,number表示蚂蚁i选择的物体数目。 步骤五中,采用交换邻域的爬山搜索算法。所谓交换领域,就是把背包问题( KP)的解x中的某一个装入物品从背包中取出,同时把某一未装入背包的物品放入背包,这样形成的解的集合就是解x的交换邻域N2(x),用数学描述如下: 其中:[I0(x)]表示未装入背包的物品合集,[I1(x)]表示装入背包的物品合集。 3 数据分析 为了验证算法设计的有效性,采用Python3.7以及NumPy科学计算库对算法进行编程实现,同时将本文的改进算法与一般的GA、ACO算法以及文献[16]说明的混合算法进行程序编写、结果测试和对比。本文采用的测试算例来自http://elib.zib.de/pub/mp-testdata/ip/sac94-suite/index.html中的部分例子。文中算法采用参数如下:最大迭代次数N=200,变异概率Pm=0.05,交叉概率Pc=0.45,解集大小size=15,初始信息素浓度矩阵ph=[1,1…,1],每条路线信息素更新总量Q=1,信息素挥发因子ρ=0.5,启发因子α=2,能见度因子β=3。 此外,為确定一个较好的循环次数N1的值,通过对一般GA运行10次后得到的结果,分析斜率突变前后的值,选取N1=50,如图1所示。 将4种算法(算法1是本文的改进算法,算法2是普通GA算法,算法3是普通ACO算法,算法4是采用文献[16]的混合算法)运行100次后得到的结果进行对比,如表1、表2所示。 表1结果显示,算法1和算法2求得的最优解好于算法3和算法4,对于采用的测试例子约高出10%。 表2结果显示,算法3和算法4的收敛速度比算法1和算法2更快。其中算法4最快,算法3次之,而算法2最慢,基本上与其它3种算法相差1~3个数量级。 以上仿真结果表明,在求解0/1 MKP问题上,在保证解精度的前提下,本文提出的方法在求解效率上比传统的GA提高了一个数量级。而在求解速度上,虽然本文提出的方法与算法3和算法4相比收敛速度较慢,但还在一个数量级内。所以,如果对所求解的质量要求很高,本文提出的改进算法会是一个很好的选择。 4 结语 通过充分分析遗传算法和蚁群算法之间的优缺点,以及一些混合算法的不足,本文提出了一种新的混合方式,通过采用这种混合方式设计了一种算法。本文在充分发挥遗传算法和蚁群算法优点的同时,基于生成解的特点,采用不同的方法处理每轮迭代中的不可行解。此外,为了优化最终解的稳定性,引入了交换邻域的爬山法。对比实验表明,在保证求解精度的前提下,本文算法能够更好地减少求解的迭代次数。 本文使用的测试参数在中低维度(5个背包,30个物体)的背包上表现较好,但在高维度问题上需要另外设定相关参数。今后将对如何自动依照求解规模调整参数这一课题进行研究。 本文研究了0/1背包问题的一种求解算法,而现实环境中还存在一个背包选择同一个物体多次的问题(比如工厂同一类型的产品有多个,而且机台也可以同时处理同类型的多个产品)。在这种更普适的情况下,解的元素会有除0,1以外的其它值。如何将背包问题与实际生产问题相结合,合理设计和改进解的结构与算法(比如GA中的变异操作),以改进求解效率和求解质量,也是需要进一步研究的课题。 参考文献: [1]KARP R M. Reducibility among combinatorial problems[M]. New York:Plenum Press,1972. [2]田烽楠,王于. 求解0-1背包问题算法综述[J]. 软件导刊,2009(1):59-61. [3]HASSANIEN A E,EMARY E. Swarm intelligence principles, advances, and applications[M]. Boca Raton:CRC Press, Inc. 2015. [4][日]玄光男,林林. 网络模型与多目标遗传算法[M]. 梁承姬,于歆杰,译.北京:清华大学出版社, 2017. [5]武廣号,文毅,乐美峰. 遗传算法及其应用[J]. 应用力学学报, 2000, 23(6):9-10. [6]李士勇,陈永强,李研. 蚁群算法及其应用[M]. 哈尔滨:哈尔滨工业大学出版社,2004. [7]王熙照,贺毅朝. 求解背包问题的演化算法[J]. 软件学报,2017(1):391-399. [8]刘雪静,贺毅朝,吴聪聪,等. 基于细菌觅食算法求解折扣0-1背包问题的研究[J]. 计算机工程与应用,2018(8):1204-1210. [9]高思齐,邢玉轩,肖侬,等. 求解01背包问题的贪婪蛙跳算法[J]. 计算机科学,2018,45(7):79-83. [10]AZAD M A K,ROCHA A M A C,FERNANDES E M G P. Improved binary artificial fish swarm algorithm for the 0-1 multidimensional knapsack problems[J]. Swarm & Evolutionary Computation, 2014(14):66-75. [11]ZOU D,GAO L,LI S,et al. Solving 0-1 knapsack problem by a novel global harmony search algorithm[J]. Applied Soft Computing, 2011, 11(2):1556-1564. [12]郭丽萍, 申秋慧. 利用改进萤火虫算法求解0-1背包问题[J]. 软件导刊,2016(1):54-56. (责任编辑:杜能钢) 收稿日期:2019-04-24 作者简介:余典(1995-),男,电信科学技术研究院硕士研究生,研究方向为工厂排程优化。

