密封环支撑边界条件对机械密封端面变形的影响

王金红，陈志，刘凡，李建明

（四川大学化学工程学院，四川成都610065）

引 言

目前，关于机械密封的研究主要集中在摩擦副的结构、端面形貌、温度场和振动影响分析方面，使密封环变形的因素主要有界面压力分布、热分配、密封环直径、弹性模量和传热系数等[1-2]，其中弹性模量和传热系数与摩擦副的材料相关。在现阶段对机械密封的研究中，考虑的因素都比较单一化，多数没有考虑辅助密封O形圈支撑条件对机械密封端面变形的影响。而实际上在机械密封设计中，辅助密封以及推环有不同的结构形式，那么这些不同的补偿环组件设计对密封性能有何影响，目前少有报道。由于机械密封的密封环是通过O形圈支撑在轴上或者密封腔上，当O形圈与之接触的动、静环端面的支撑边界条件发生了变化，在一定程度上会影响密封性能[3]。动环O 形圈的压缩率、尺寸和安装位置对机械密封的密封性能[4]、动环浮动性及追随性影响较大，同时对动环的支撑刚度和端面的变形也有非常大的影响。因此，需要研究辅助密封O 形圈不同结构设计对机械密封性能的影响。

近年来，实验方法越来越被数值模拟所取代，数值模拟方法有助于研究磨损对接触压力的影响和密封件的变形，这是通过实验方法难以获得的。通过验证的数值方法可以预测更多类似的复杂问题[5]。机械密封变形理论的主要研究方法目前有三种：圆环理论、边界元法和有限单元法[6]。摩擦副的变形对密封性能影响较大的是摩擦副端面变形，两端面的变化是热效应和力载荷共同作用产生的，二者不是彼此独立的，而是需要通过耦合计算得到正确解[1]。有限元分析时需要考虑结构应力和热应力的耦合作用，国内外学者对机械密封的热结构耦合场做了大量的研究。Samant 等[7]利用有限元法，对机械摩擦副进行热结构耦合，提出了三种用于耦合场分析的基本思路。Tournerie 等[8]建立了摩擦副的瞬态结构模型，并使用影响系数法进行了热-弹性耦合计算。Lai等[9]使用CSTEDY 软件建立了耦合模型，可预测摩擦副变形、温度、端面液膜厚度和泄漏率等密封性能。廖和滨等[10]采用间接耦合方法建立了机械密封动、静环的温度场轴对称分析模型，将求解出的温度场作为已知载荷施加到节点上进行结构分析，从而完成耦合场分析。周剑锋等[11]借助有限元方法和人工神经网络，研究了摩擦副端面间液膜摩擦热与端面热变形的耦合过程。钟汝琳[12]利用FLUENT对机械摩擦副温度场进行了数值模拟。

目前，对于机械密封辅助密封圈的有限元分析主要集中在单一结构下的O 形圈的压缩变形、摩擦副端面泄漏的问题上[13-15]。密封端面的泄漏为主泄漏点，密封环是通过辅助O 形圈支撑在轴上的。而密封环的支撑边界条件，即辅助密封与密封环的不同结构设计是否会影响摩擦副的端面变形，目前还未有文献报道。针对相同的摩擦副结构和尺寸，本文主要研究了动环的三种不同的橡胶O形圈支撑方式，这三种结构设计如图1 所示，这里动环都是通过O 形圈的过盈量起到支撑作用，并密封流体沿着轴向的泄漏通道。由于材料的弹性模量影响密封环的转角和变形[16]，本文中也研究了材料对变形的影响。通过对O 形辅助密封圈不同支撑方式的机械密封模型的数值模拟，得到不同支撑方式下机械密封端面变形的规律，为选择密封设计提供理论基础。

1 结构及计算模型

1.1 结构模型

机械密封的基本元件有：摩擦副（动环和静环）、弹性元件（弹簧或波纹管）、辅助密封圈（O 形圈）、传动件和防转销等。根据动环O形圈支撑方式的不同有本文研究以下三种密封结构模型，如图1所示。图1(a)为结构一，弹簧力通过推环直接作用在动环上，动环O 形圈上仅受介质压力的作用；图1(b)为结构二，弹簧力通过推环作用在动环O 形圈上，再传递到动环上，同时动环O形圈上还受介质压力的作用；图1(c)为结构三，弹簧力通过推环作用在动环O形圈上，再传递到挡圈上，通过挡圈再传递到动环上，同时动环O 形圈上还受介质压力的作用。三种结构模型中，静环的O 形密封圈和支撑方式是相同的，结构三是在高压下防止辅助密封圈被挤出的一种结构设计。根据机械密封结构为回转体的特点，计算模型可以简化为平面轴对称模型，通过平面轴对称模型来模拟三维结构，并且通过对轴径向位移的控制来模拟O形圈的预紧压缩状态，由于轴、压盖等相对O形圈来说刚度很大，因此忽略其变形，即将其与O形圈接触的部位视为刚体边界，采用线代替。

图1 三种机械密封结构简图Fig.1 Simplified diagram of three mechanical seal structures

1.2 摩擦副端面间隙类型

机械密封的摩擦副在安装、使用中的端面会发生变形。由于摩擦副端面的变形，端面间隙由理想的平行型变为收敛型或发散型如图2所示。密封端面间的密封为主密封，轴向变形是决定密封性能的决定因素。坐标体系如图所示，选取图中X 坐标轴为研究路径，且规定了沿Y 轴正方向的位移为正。图2 中，α 为端面轴向锥度[17]。图2(b)中α 为“+”，形成收敛间隙；图2(c)中α为“-”，形成发散间隙。

1.3 计算模型

1.3.1 模型材料、工况及物性参数 模拟计算机械密封的工况参数为：转速2950 r/min，压力1 MPa；冲洗介质为去离子水，温度20℃，其物性为：ρ =1 g/cm3，ν=10-6m2/s，λf=0.6 W/(m·K)，Cp=4200 J/(kg·K)，

Pr=7.02[18]。本文模拟中首先针对工程实际应用的摩擦副配对（动环、静环材料均为SiC）进行研究，然后再讨论碳石墨-SiC 的端面配对。辅助密封O 形圈材料选用丁腈橡胶，密封挡圈选择聚四氟乙烯，其相关的参数见表1。

由于O形圈的材料为丁腈橡胶(NBR)，是一种典型的超弹性材料，其特性呈现复杂的非线性变化。所以采用常用的高阶Mooney-Rivlin 本构模型来描述O形圈的力学行为[20]。

表1 摩擦副和O形圈的材料参数［19］Table 1 Material parameters of friction pairs and O-rings［19］

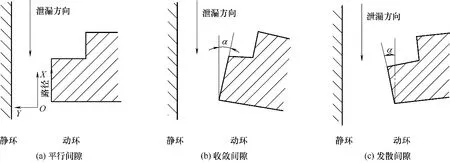
图2 摩擦副端面间隙形式Fig.2 Gap forms of end face of friction pair

Mooney-Rivlin模型是基于材料变换理论和不可压缩各向同性超弹性材料的Mooney有限变形弹性理论。假设单位体积的储能函数是柯西-格林变形张量的不变函数，建立了橡胶材料的应变能函数[21]

与Mooney-Rivlin 模型相比，具有更高阶项的Mooney-Rivlin 模型更适合于填充和非填充橡胶材料[22]。其具体形式如下

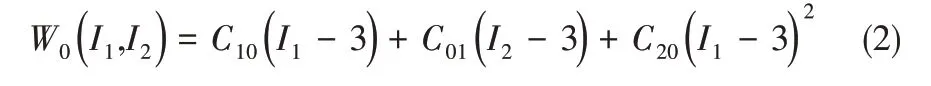
式中，C10=0.923，C01=0.239，C20=0.010。

1.3.2 有限元模型 在进行模拟的过程中，将结构一的O 形圈与摩擦副，结构二的O 形圈与摩擦副以及推环，结构三的O形圈、挡圈与摩擦副以及推环分别视为整体，对该整体组件进行受力和温度场的数值模拟，组件之间的力视为内力。本文研究中，三种密封结构的静环组件是相同的。O 形圈、动环及静环在分析计算时均选用二维四节点结构单元PLANE182，热分析时选用二维四节点热单元PLANE55。模型中的接触类型为刚性体-柔性体接触，为面面接触，接触单元采用CONTA172，目标单元采用TARGE169。为了减少渗透，设置接触单元的法向接触刚度因子（FKN）为2[23]。对模型进行网格划分后，在O形圈、摩擦副及刚体边界之间可能接触的边界建立接触单元对。计算中结构一网格如图3 所示。另外两种结构的网格划分方法相同，不再赘述。

2 边界条件及载荷

2.1 力学模型及边界条件

为方便机械密封耦合分析，压力载荷做以下简化：(1)动环外周和背部以及O 形圈与介质液接触段的表面受到均匀分布的介质压力p1；(2)动环端面受到沿径向线性分布的流体膜压p1～0；(3)动环背部作用面受到单位端面面积上均匀分布的弹簧等效压力ps。需要指出的是，由于结构的特点，只有与介质接触区域才受压力作用，故针对特定的区域需要将力施加在相应的节点上。图4为结构一的受力边界图，结构二和结构三受力边界图不再赘述。三种结构O 形圈的配合尺寸相同，三种支撑结构下的O 形圈的预压缩率相同，动环O 形圈直径为3.65 mm，压缩率为12.3%。静环O 形圈直径为5.15 mm，压缩率为12.5%。

2.2 热边界条件

机械密封端面接触为边界摩擦，模型的热边界简化为三种形式，如图5 所示。另外两种结构与此相同，不再赘述。

图3 结构一的网格划分Fig.3 Grid partition of structure 1

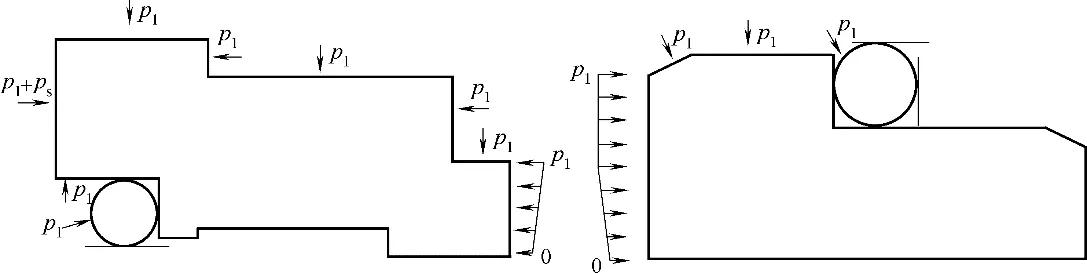
图4 结构一的受力边界图Fig.4 Stress boundary diagram of structure 1

图5 结构一的热边界条件Fig.5 Thermal boundary conditions of structure 1

2.3 热通量及摩擦热

机械密封为接触式密封，接触端面一般为混合摩擦状态，端面热通量的计算式[15]如下

式中，摩擦系数f根据API682 取0.07，端面比压按照文献[4,24]中公式计算，为0.41 MPa。

端面总摩擦热是由端面各点的热流率积分求得，即

式中，A为密封端面面积。

2.4 对流传热系数

要准确描述摩擦副表面与密封介质的对流传热系数非常困难，采用经验公式计算对流传热系数，动环和静环的介质换热系数可分别按式(5)和式(6)计算[25-27]

所用模型中Dr=0.0972 m，冷却水冲洗量为5 L/min。

2.5 热量分配

摩擦热与端面的变形有直接的关系，由于动静环的转速、材料、几何参数、摩擦副对介质的传热系数不同，导致摩擦热在端面的热量分配也不同。动静环热量分配系数可根据式（7）计算[11,27-28]

其中，

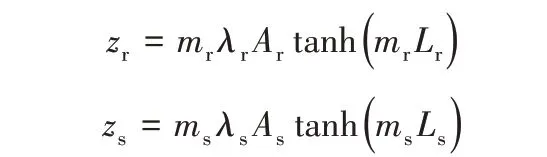
相关参数由文献[27]中公式计算得出。

2.6 网格无关性验证

为验证网格大小对模拟结果的影响，以结构二为对象进行热分析，用不同网格尺寸对结构二的温度结果进行网格无关性检验。

根据表2 的网格无关性检验结果，发现网格尺寸到0.2 mm 时计算结果趋于稳定，并且可以看出几种网格的计算结果相差很小，综合考虑计算精度和时间，本文网格尺寸采用0.2 mm，此时动环模型网格数为5472，节点数为5522。图6 为此时结构密封环的温度分布云图。

表2 网格无关性检验Table 2 Grid irrelevance test

图6 摩擦副的温度云图Fig.6 Temperature nephogram of friction pairs

3 计算结果与分析

3.1 结构分析

结构分析是指对机械密封在静止状态下，考虑力变形的分析。图7为三种结构的机械密封在结构分析时的端面变形图，图7(a)为动环密封端面变形图，图中水平轴线代表着密封端面的路径（路径方向见图2），0 对应内径处，5 对应外径处，纵向轴为密封端面沿轴向产生的变形。可以用端面内径和外径处的相对变形量来衡量端面的变形程度[29]，此时动环密封端面变形规律为：结构一端面变形＞结构二端面变形＞结构三端面变形。图7(b)～(d)分别是结构一至结构三的摩擦副端面在变形后的位置图。动环：结构一锥角为-1.719×10-3(°)，结构二锥角为-1.146×10-3(°)，结构三锥角为-5.73×10-4(°)；静环锥角为-1.15×10-3(°)。此时动、静环密封端面锥角均为“-”，即摩擦副组合后形成发散间隙。结构一此时锥角最大，发散程度更高。结构三发散锥角最小。

为进一步研究密封环的支撑边界的影响，讨论动环和O 形环之间的接触应力状态是关键。图8 是三种不同结构的接触应力分布。为了考虑支撑边界条件的影响，采用控制变量法。得到结构一O 形圈与动环的最大接触应力为2.62 MPa，结构二的最大接触应力为2.30 MPa，结构三的最大接触压力为2.39 MPa。结构一的接触应力最大，结构二的接触应力最小，且各结构的最大接触应力均发生在径向接触点，这是因为O 形圈装配后最大预压缩发生在径向接触点的缘故。

图7 结构分析时机械密封端面变形Fig.7 Deformation of mechanical seal face in structural analyses

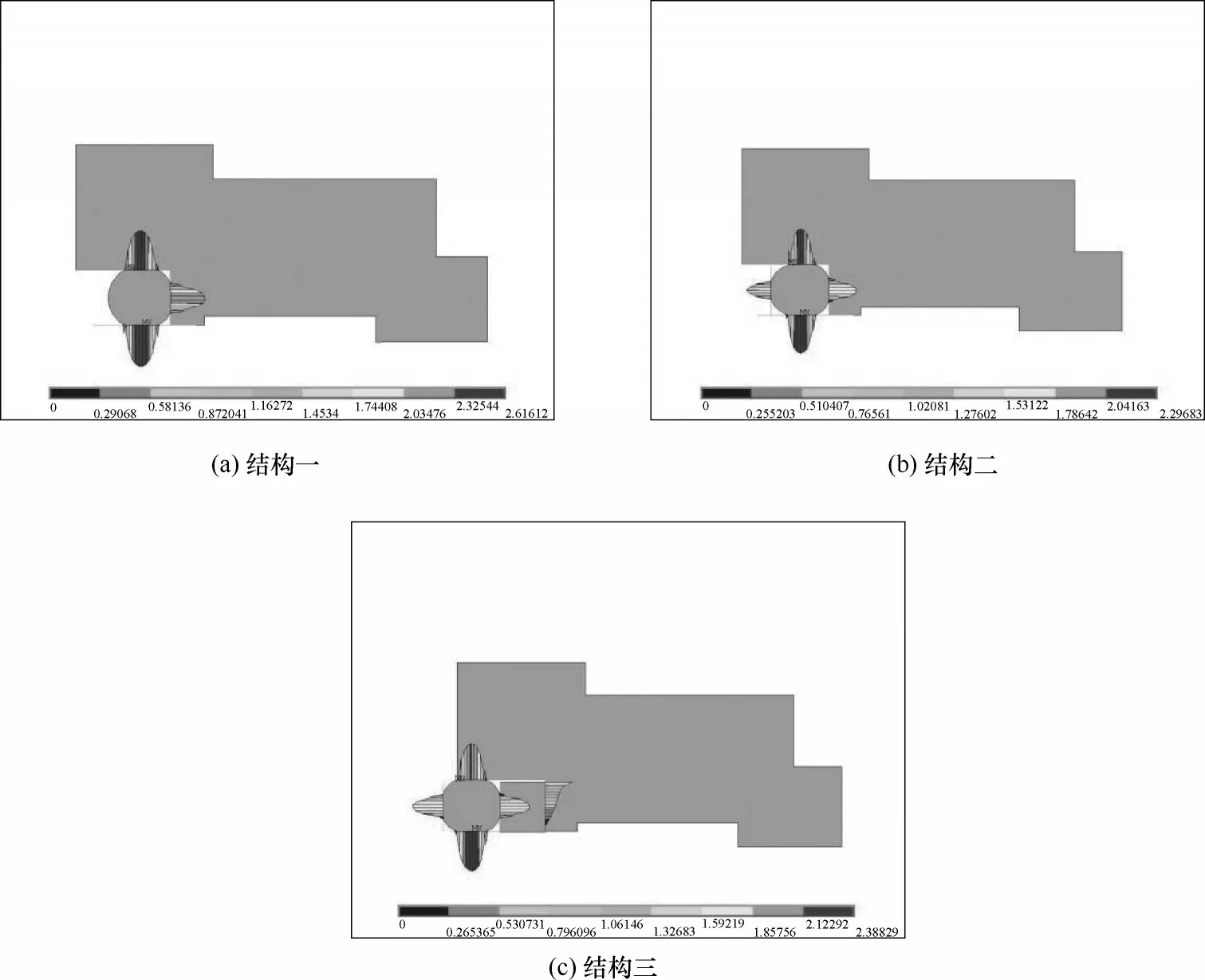
图8 不同结构橡胶O形圈与动环之间的接触力分布（动环SiC、静环SiC）Fig.8 Contact force distribution between rubber O-ring and rotating ring with different structures(both rotating ring and static ring SiC)

分析接触应力对密封环端面变形的影响发现：(1)结构一和结构二相比，O 形圈与动环接触位置相近，结构一的接触应力从云图显示大于结构二的接触应力，结合图7，发现此时结构一的端面变形锥角大于结构二，显然推环直接接触O 形圈的结构对缓解静压下端面变形是有利的。(2)由图7(b)和图7(c)的对比发现，虽然结构三得到的最大接触应力比结构二大，但是对比图7(a)可知，结构二的密封端面变形锥角大于结构三。这是因为结构三的O形圈相对于结构二的位置向左移动了一个挡圈的宽度，动环由O 形圈和垫圈共同支撑密封环，可以使动环转动能量下降，导致端面变形锥角变小。可见O 形圈的支撑点的位置和支撑结构设计会影响密封环的变形。

3.2 热结构耦合分析

采用间接耦合方法，将热分析中求得的温度场作为体载荷施加到结构分析中，来模拟机械密封在转动时的状态。在进行热分析的时候，假设不考虑搅拌摩擦热的影响，只考虑端面产生的摩擦热以及水与密封环的对流换热。耦合分析时，依据公式，三种结构的不同部位的对流传热系数一致，即：动环传热系数为14790 W/(m2·K)，静环传热系数为640 W/(m2·K)。

图9 为SiC 对SiC 摩擦副三种结构在热结构耦合后的摩擦副端面变形图。三种结构的密封端面变形组合锥角均为收敛间隙，并且他们形成锥角相差较小，三种密封支撑边界条件的不同在热结构耦合后对端面变形的影响较小。动环的端面锥角分别为：结构一锥角为1.146×10-2(°)，结构二锥角为1.153×10-2(°)，结构三锥角为1.156×10-2(°)；静环的端面变形锥角为-5.729×10-4(°)。发现运转后，三种支撑边界下，动环端面的锥角由“-”变为“+”，外径处形成收敛间隙，密封均是有效的。

为了研究摩擦副材料配对对机械密封环性能的影响，在其他条件不变情况下，动环改为石墨，静环材料保持为SiC，再次进行模拟。端面变形结果见图10。结构一碳石墨动环的变形锥角为-1.146×10-2(°)，结构二碳石墨动环的变形锥角为-5.730×10-3(°)，结构三的碳石墨动环的变形锥角为3.438×10-3(°)，静环的端面变形锥角为-5.728×10-4(°)。图中结构三端面之间形成收敛间隙，结构一和结构二端面之间形成发散间隙。由此可见，摩擦副的材料对密封端面的变形有很大的影响，材料的弹性模量影响密封环的转角和变形，该结论与文献[16,30]一致。同时，材料不同时，动环的热导率也不同，动、静环的热通量重新分配，受热边界条件发生变化。相同的支撑边界下，动、静环的材料的配对对摩擦副端面的间隙形状有较大影响，从而影响密封性能。

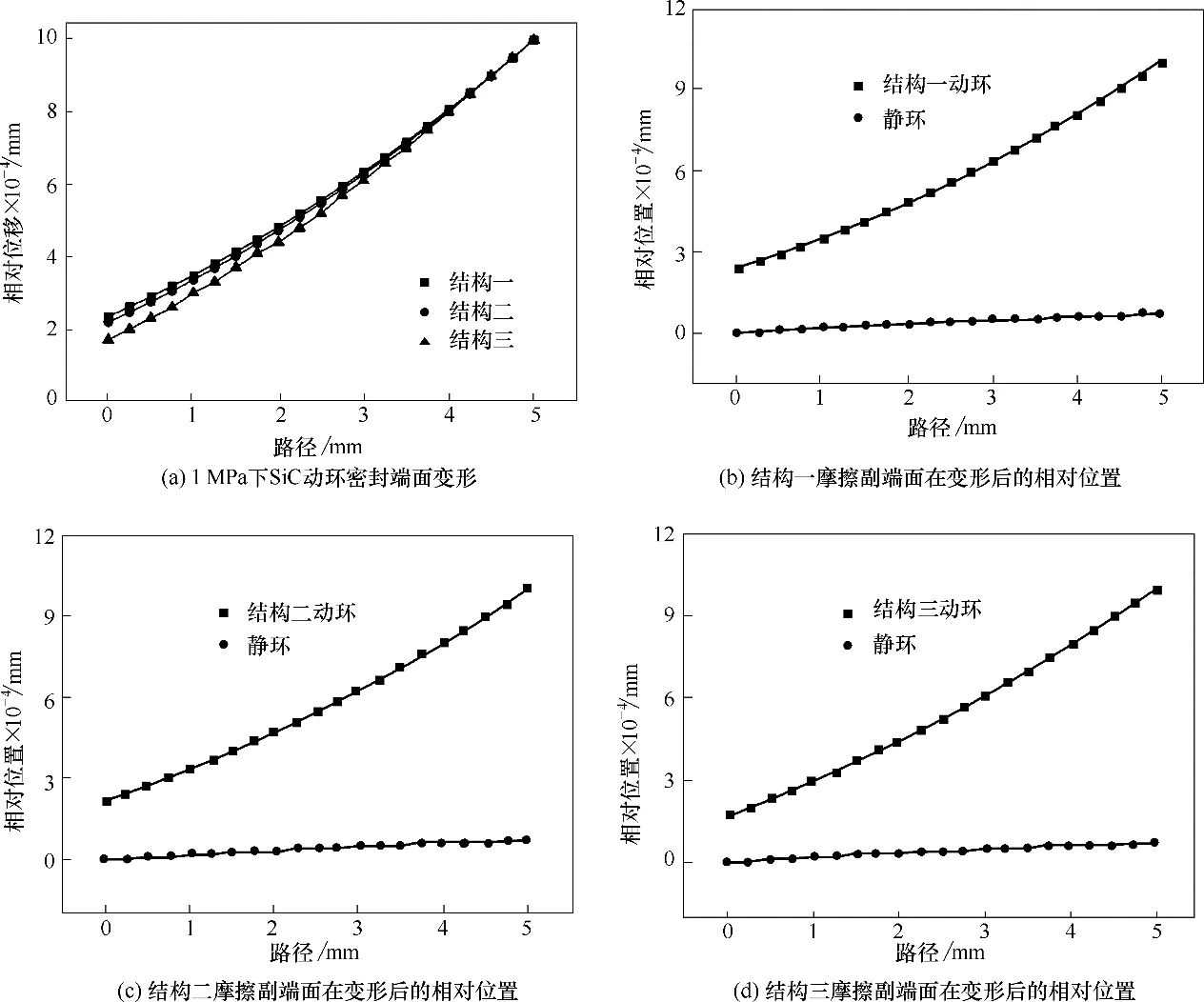
图9 耦合分析时机械密封端面变形（动环SiC、静环SiC）Fig.9 Deformation of mechanical seal face in coupling analyses（both rotating ring and static ring SiC）

图10 动环碳石墨、静环SiC配对摩擦副结构三的变形Fig.10 Deformation of paired friction pair structure of rotating ring carbon graphite and static ring SiC

对比分析图9、图10，发现在支撑边界、热边界条件完全一致的情况下，动环材料由SiC 改为碳石墨，就会对端面变形产生极大的影响，端面原有的收敛间隙有时（结构一、结构二）会变成发散间隙。本文研究的石墨属于较高等级热导率系列，与SiC相近。说明碳石墨环作动环时，由于弹性模量小，离心力引起的端面变形较大，有可能会导致端面产生发散间隙，这点需要注意。

4 结 论

建立了三种不同支撑方式的机械密封结构，分别将动环和O 形圈或者垫片、静环和O 形圈作为整体模型对象进行研究，进行了摩擦副端面变形规律的分析。研究得出以下结论。

(1)结构分析结果表明：机械密封静态时在摩擦副端面变形近似于呈线性分布，动、静环端面变形锥角都为“-”，摩擦副端面形成发散间隙。密封环支撑边界条件的改变会影响密封环的端面变形，从而影响静态时机械密封性能。结构三（即弹簧力通过推环作用在动环O 形圈上并传递到挡圈上，再传递到动环上的结构）在静压时发散锥角最小。

(2) 热结构耦合分析结果表明：机械密封运转时，由于摩擦热和离心力的作用，摩擦副端面变形呈非线性分布。动环O 形圈的支撑边界条件、摩擦副端面材料配对会对端面变形产生较大影响。当摩擦副材料采用SiC 对SiC 时，结构三在运转时形成的收敛锥角最大，结构一（即弹簧力通过推环直接作用在动环上的结构）在本工况下形成的收敛锥角最小。

(3)不同材料配对的摩擦副热结构耦合后的结果表明：动环、静环均采用SiC 时，三种结构摩擦副端面形成收敛间隙；但碳石墨环作动环、静环采用SiC 时，结构一、结构二（弹簧力通过推环作用在动环O 形圈上，再传递到动环上）为发散间隙，结构三仍然为收敛间隙。因此，动环O 形圈的支撑边界条件的不同会影响机械密封的端面变形行为。端面的间隙与动、静环材料的配对和结构设计有关。

符 号 说 明

Ar——动环当量圆筒端面面积，m2

As——静环当量圆筒端面面积，m2

C——比热容，J/(kg·K)

C10,C01,C20——材料常数

Dr——动环外周的当量直径，m

E——弹性模量，MPa

f——摩擦系数

fr——动环热量分配系数

I1,I2——应变张量的不变量

k——热导率，W/(m·K)

Lr——动环当量筒体长度，m

Ls——静环当量筒体长度，m

mr——动环散热系数，m-1

ms——静环散热系数，m-1

Pr——Prandtl 数，表征流体物性对对流传热过程的影响

pc——端面比压，MPa

q——热通量，W/m2

Rea——介质的横向绕流效应

Rec——介质的旋转搅拌效应

r——动环端面半径，m

Ss——静环凸缘外周与箱内壁间的间隙，m

W——应变能密度函数

X——修正系数，一般可取1

α——热膨胀系数，K-1

α′——液膜与密封环端面的传热系数，W/(m2·K)

ε——泊松比

λf——介质的热导率，W/(m·K)

λr——动环材料的热导率，W/(m·K)

λs——静环材料的热导率，W/(m·K)

ν——介质的运动黏度，m2/s

ρ——密度，g/cm3

ω——动环环旋转角速度，rad/s

下角标

r——动环

s——静环