催化裂化提升管进料段喷嘴射流运动-扩散特性的分析

许峻，范怡平，钱筱婕，闫子涵，卢春喜

（1 中国石油大学（北京）重质油国家重点实验室，北京102249； 2 中国石油大学（北京）机械与储运工程学院，北京102249）

引 言

催化裂化提升管反应器是目前炼化企业催化裂化工艺的核心生产装置，其工作状况直接影响企业的经济效益。按照功能自下而上可将提升管反应器分为预提升段、进料混合段、快速反应段和出口分离段[1]。进料混合段是油剂接触混合的关键区域，其内油剂的混合状况将直接影响产品分布和目标产品收率[2-3]。由于进料段内涉及多股射流与气固两相流混合，流场十分复杂，以往研究多集中于提升管整体的流动特性[4-7]，发现管内轴向呈现“上稀下浓”的形态，径向存在颗粒浓度边壁高、中心低的“环核分布”结构。而鄂承林等[8-9]通过实验研究进料段内不同高度的油剂混合接触状况，发现该区域沿轴向自下而上，催化剂颗粒出现先向中心后向边壁聚集的变化趋势。陈昇等[10]则利用数值模拟考察了不同角度进料射流对提升管流场分布的影响，指出进料角度越大，颗粒边壁返混作用越强，并提出应将向上进料改为向下进料的优化方案。

伴随原料油的重质化、劣质化，提升管反应器内结焦，尤其是进料混合段的结焦问题日益突出。针对进料段的结焦原因，以往研究多认为是原料油气经喷嘴喷射至对侧边壁所致[11]，但范怡平等[12-13]通过大型冷模实验发现，提升管进料段喷嘴射流存在二次流现象，因而提升管进料混合段喷嘴以上部分可分为主射流影响区段、二次流影响区段和混合发展区段。其中催化剂颗粒在二次流影响区严重返混，油气过度裂化，是造成边壁结焦的主要原因。

针对二次流的理论分析，Fan等[14]通过引入空气动力学中的Kutta-Joukowski 横向力理论，解释了提升管内催化剂颗粒的“环核分布”和二次流的产生机理，但并未讨论量化模型。Yan 等[15]利用射流理论给出了喷嘴主射流及二次流的流线方程，但其二次流中心流线方程是在主流中心流线方程基础上，通过实验数据校正相关系数得到的，未能结合Kutta-Joukowski 横向力理论，造成对于二次流后期发展扩大阶段的描述与实测结果不符。因此，本文分析了射流相与颗粒相之间的相互作用，提出了二次流产生机理模型，并将Kutta-Joukowski 作用力引入，给出了更符合实验结果的二次流中心流线方程。

1 射流二次流的产生机理模型

1.1 提升管内的Kutta-Joukowski横向力现象

催化剂颗粒随预提升蒸汽一起向上运动的同时，沿提升管径向方向颗粒速度中心高、边壁低[16]，进而形成颗粒浓度中心低、边壁高的分布情况。为便于说明Kutta-Joukowski 横向力对颗粒“环核分布”结构所起的作用，将中心稀相颗粒与边壁密相颗粒连续介质化，构成如图1所示的浓稀两相（假设相内各自均匀）。对于图1 中某一单连通域内的颗粒群，其自身沿提升管轴向-径向的速度梯度会使其产生涡量Ω，进而产生旋涡强度J（并非真正意义上的旋转，旋涡强度会形成一个“等效的”速度环量Γ），在受到预提升蒸汽来流的作用时，会产生类似于空气动力学中的Kutta-Joukowski 升力现象。Kutta-Joukowski 升力的基本思想[17]是，当某一物体周围存在一个速度环量Γ，若此时另一股来流以相对速度Vs流经该物体，则会产生一个垂直于来流方向的升力Fk（升力方向为将来流方向逆环量旋转90°）。因此，颗粒群就会受到一个垂直于预提升蒸汽速度方向，即水平方向的力Fk的作用。在图1中，颗粒群就受到一个指向边壁的力（具体原因后文分析），由中心向边壁聚集。由于提升管内的Kutta-Joukowski 力Fk为水平方向，因此将该“升力”称为Kutta-Joukowski 横向力。Kutta-Joukowski 横向力Fk的表达式如式(1)所示[18]

流体力学中的Stokes定理阐述了速度环量Γ 与旋涡强度J的关系，对于二维平面，旋涡强度又与涡量（速度梯度）密切相关，如式(2)所示[19]

图1 Kutta-Joukowski力对提升管内颗粒群的作用Fig.1 Influence of Kutta-Joukowski force on particles

因此，提升管内的Kutta-Joukowski 横向力Fk可以用式(3)表示

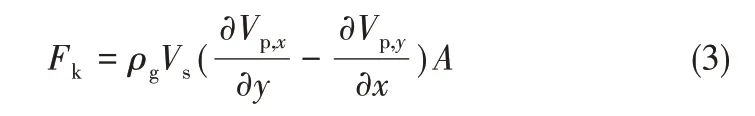
式中，A 表示提升管内某一单连通域颗粒群的面积。

值得注意的是，Kutta-Joukowski 力Fk产生的前提是颗粒群存在速度环量，而以上分析可知，以提升管内催化剂颗粒群为研究对象，由其自身速度梯度形成的涡量是普遍存在的，进而量化为等效的颗粒群速度环量，因此将Kutta-Joukowski 力Fk引入提升管内是可行的。

1.2 本文模型的简化设定

提升管进料喷嘴附近的流动状况可以描述为“三相混合（喷嘴原料油气相、催化剂固体颗粒相、预提升蒸汽相）、高度湍动”的复杂流场。为便于分析，做出如下简化[15]：（1）射流是不可压缩的二元流动；（2）喷嘴射流对入口以下不产生影响；（3）催化剂颗粒在远离喷嘴入口区域仅做轴向运动。

如图2所示，将提升管分为三个区域，并建立平面直角坐标系，坐标原点在提升管中心。区域Ⅰ为进料喷嘴截面以下，认为喷嘴射流对该区域不产生影响，提升管内处于稳定的“环核分布”结构。区域Ⅲ为远离喷嘴区域，认为进入该区域气固相已经充分发展，且二次流与主流已经汇合完毕无法区分，管内同样处于稳定的“环核分布”结构。而两者之间的区域Ⅱ即为进料射流与预提升催化剂来流的混合接触区域，二次流在该区域形成并发展。其中，二次流与边壁夹角为γ，主射流与边壁夹角为β。

对于图2 区域Ⅰ和区域Ⅲ，提升管内为携带催化剂颗粒轴向向上运动的预提升气。根据模型假设，以及范怡平等[13]、李晨等[20]的分析，区域Ⅰ和区域Ⅲ内颗粒径向速度沿y 轴大小不再变化，即式(3)中径向速度沿轴向的梯度项∂Vp,x∂y = 0，则对于x轴正方向内某一单连通域的颗粒群，单位面积（A=1）上的Kutta-Joukowski横向力如式(4)所示

由于颗粒速度中心高，边壁低，式(4)中轴向速度沿径向的梯度项∂Vp,y∂x ＜0，即

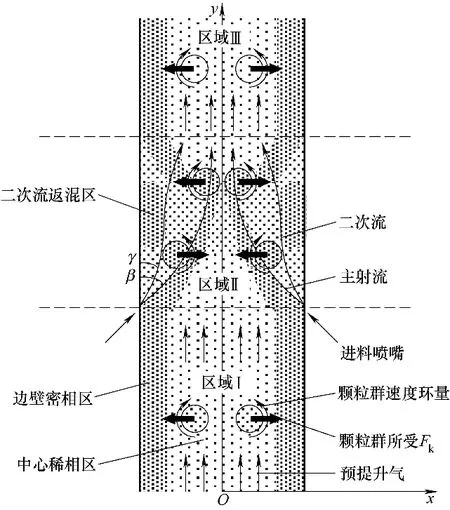
图2 喷嘴向上提升管进料段气固相混合过程Fig.2 Gas-solid phase mixing process of nozzle upward riser feed section

根据习惯约定，速度环量以逆时针方向为正方向。那么x正半轴内的颗粒群速度环量即为逆时针方向，由Kutta-Joukowski 定理可以判断该单连通域内的颗粒群所受的Kutta-Joukowski 横向力指向x 轴正方向。由于对称性，x 轴负方向内的颗粒，则受到指向x 轴负方向的Kutta-Joukowski 横向力。即颗粒有向边壁运动的趋势，从而形成管内颗粒边壁浓度高、中心低的“环核分布”结构。

当预提升气固两相运动至图2 区域Ⅱ时，聚集于边壁的催化剂颗粒与进入提升管的喷嘴射流相遇。由于射流流速一般在60～80 m/s，而预提升气速仅有3～4 m/s，因此催化剂颗粒瞬间被喷嘴射流带走。假设颗粒加速时间极短，并将连续的射流“分块”，如图3 所示，根据动量守恒定律，一部分“射流流块”将动量传递给颗粒，使其加速，而自身速度降低；另一部分“射流流块”未与颗粒接触，仍保持原动量继续运动。由此，喷嘴射流与催化剂颗粒混合接触后，射流内部将产生速度差，“高速流块”形成射流主流，以入射角β继续运动；“低速流块”则逐渐脱离主流，以式(6)的角度γ形成“二次流动”[14]。

喷嘴射流的进入使颗粒获得了径向加速度，此时对于图2 区域Ⅱ内某一单连通域的颗粒群来说，其径向速度沿轴向的梯度∂Vp,x∂y ≠0，即单位面积上颗粒群所受的Kutta-Joukowski力为

图3 气固相间动量传递模型Fig.3 Ggas-solid phase momentum transfer model

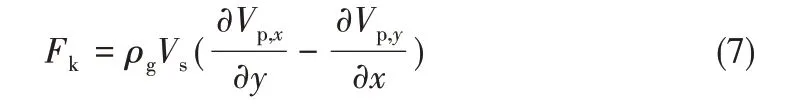
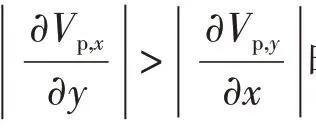
如图4 所示，以喷嘴附近某一边壁颗粒群为研究对象，考察其运动轨迹。可以看到，对于图4(1)区域，颗粒群在接触到喷嘴射流时迅速获得了最大径向速度，但此时颗粒群处于边壁浓相区，以轴向运动为主，颗粒群被“裹挟”着一起向上运动，重力作用可以忽略，因而颗粒群轴向动量损失较小。而横向穿过该区域则需要消耗极大的径向动量。所以图4(1)区域就速度梯度而言，应存在如式(8)所示的关系

即对应于上述情况(1)，此时颗粒群受指向提升管中心的Kutta-Joukowski 力Fk作用。随后，颗粒群向上、向中心运动，在图4(2)区域，颗粒群进入稀相区，重力作用逐渐明显，轴向速度相比于边壁处的轴向速度衰减加剧，而径向速度变化逐渐减小，在该区域速度梯度出现如式(9)所示的关系

图4 颗粒群运动过程Fig.4 Particle group motion process

即对应于上述情况(2)。而后，在接近提升管中心的图4(3)区域，颗粒群径向动量基本消耗殆尽，径向速度梯度也越来越小，直至小于轴向速度在管截面的梯度，如式(10)所示

即对应于上述第(3)种情况，颗粒群在该区域受到指向管壁的Fk作用。

也就是说，在图2 区域Ⅱ内，颗粒相将在Kutta-Joukowski 力Fk的作用下，出现由下至上，先向提升管中心聚集，后向边壁聚集的两种相反趋势。根据牛顿第三定律，颗粒相受到Fk，则必有大小相同方向相反的-Fk作用于射流相。由先前的分析，二次流的产生是因为射流相与颗粒相间的动量传递，因而-Fk也应当作用于二次流，而非主射流，即二次流将在区域Ⅱ内出现先向提升管边壁运动，后向中心运动，直至与主射流汇合的趋势。

至此，二次流的产生、发展、扩大直至与主流汇合的全过程都有了较为明确的解释。不过，上文并未分析操作条件（如喷嘴射流角度、提升管内表观气速等）对二次流的影响；事实上，无论Fan 等[14]针对原料油斜向上喷入还是Yan 等[15]油剂逆流接触的实验结果均表明，改变喷嘴射流角度、速度，提升管内均存在二次流现象，但是影响程度有所不同。例如Fan 等[14]发现，喷嘴射流速度增高，强化了油剂混合，但却导致边壁区域催化剂返混剧烈。李晨[20]等指出Kutta-Joukowski 力Fk随颗粒循环量增大而增大，而表观气速的增大对其影响较小。可见，二次流是提升管内射流与颗粒相互作用而出现的固有现象，操作条件的改变仅影响二次流的扩展范围，并不影响其发展历程，因此本文对二次流的全周期过程分析具有一般性。

2 射流二次流中心流线模型

根据Yan等[15]建立的射流中心线方程

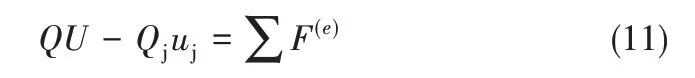
式中，Q = 2bρjU，为考察射流微元段末端截面处射流的质量流率；Qj= 2bρjuj,为喷嘴出口截面处的射流质量流率；F(e)为作用于质点系上的外力主矢。

理想情况下，对于射流主流，预提升来流的动压和射流卷吸压力叠加构成合外力主矢∑F(e)。对于二次流，Yan 等[15]模型中仍采用射流主流的∑F(e)作为二次流中心线方程的合外力主矢，并利用实验数据修正而得到二次流中心线方程，这导致其二次流模型仅适用于特定操作条件下。而由本文之前的分析可知，二次流中心线方程中的合外力主矢∑F(e)实质上应由Kutta-Joukowski 力Fk构成。因此，由式(3)与式(11)，并考虑单位面积上射流相与颗粒相的混合，本文提出的二次流中心线方程如式（12）所示

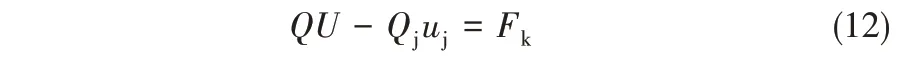
即

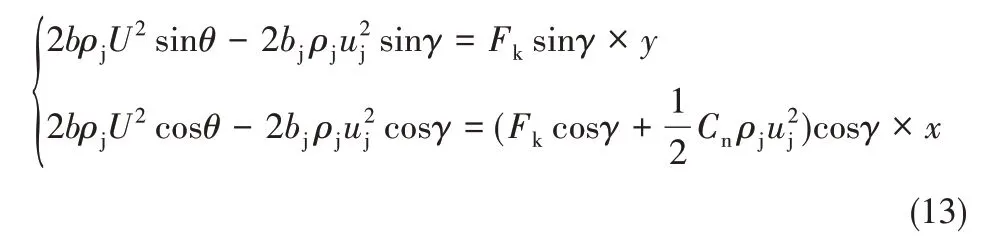
式(13)中用上式除以下式得

积分得

其中

式(15)即为二次流中心流线方程。然而此式在计算时存在困难，Fk的表达式中存在偏导数，而颗粒运动的速度分量Vp,x和Vp,y的表达式又难以得到。因此在计算时考虑使用单位面积上的Fk的定义式[19]

M 表示偶极子的强度（偶极矩），针对提升管进料混合段，可将管壁喷嘴出口处看作一对源和汇叠加而成的偶极子（即管壁外侧喷嘴射流全部流入为汇，内侧喷嘴射流全部流出为源），流量qv即为喷嘴出口流量。同时，根据李晨[21]的研究，以式(17)计算颗粒局部滑落速度Vs

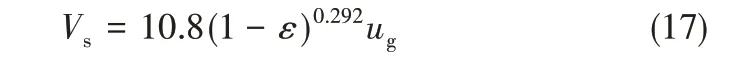
式中，ε 为局部空隙率，可由实验测得；ug为预提升气速。

至此，二次流中心流线方程中所有参数都可进行计算。

3 模型计算结果与文献的对照

由本文之前对二次流的分析可知，在提升管进料段内，二次流在管壁附近产生，沿轴向向上发展，之后逐渐向管中心扩展发散，并与进料主流汇合，最终形成管内稳定的气固相环核分布结构。由于进料段区域复杂的流动特征，文献研究多集中于该区域结构改进来优化油剂接触状况，如采用缩颈结构[22-23]、增加内构件[24]等，与本文模型相匹配的实验研究不多。因此本文模型计算结果将与现有文献报道的数值模拟和实验结果进行比较。

3.1 向上30°进料模型计算结果与数值模拟结果比较

Chen 等[25]利 用EMMS 模 型[26-27]对 向 上30°进 料的提升管内部气固流动状况进行了数值模拟，给出了进料段区域射流流动的时均分布特征，如图5(a)所示。可以看到，喷嘴射流在进入提升管后，射流对周边颗粒的卷吸作用形成了局部负压区[图5(a)圈出位置]，而不同高度局部负压区中心的连线，如图5(a)中红色虚线，就代表着射流主流中心流线沿轴向的发展趋势。而在靠近边壁附近（r/R≈0.95），存在一个压力突增区域，且越靠近喷嘴该区域压力峰值越高。这个压力突增应是颗粒在边壁滑落返混，气固相流动速度骤降而导致的。且在喷嘴附近形成一个流动速度极低的颗粒堆积区域，导致喷嘴附近压力峰值最高。结合二次流内部颗粒返混强烈[14]的特征，可以认为这个压力突增区域就代表着二次流区域，其范围就表示二次流影响范围。Chen 等通过数值模拟结果，同样认为边壁压力突增区域对应着二次流区域，但其分析认为压力“拐点”的连线，即图5(a)中蓝色虚线，表示二次流中心流线。本文认为该虚线应是二次流边界线，而非中心流线。“中心”表示两侧对称，而蓝色虚线左右两侧压力值明显不同。因此，本文认为Chen 等的模拟结果中，二次流中心流线应是压力峰值点的连线。

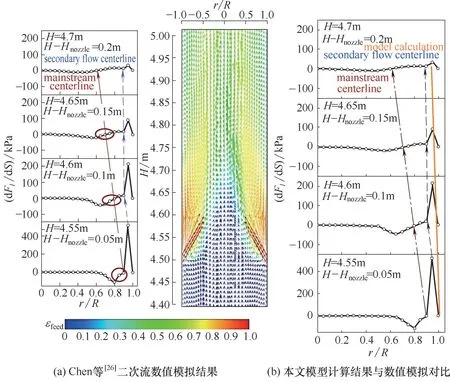
图5 30°向上进料提升管进料段二次流数值模拟与本文模型计算结果（Ug=3.28 m/s，Uj=83.3 m/s）Fig.5 Comparison of secondary flow between numerical simulation and model calculation of 30°upward feed riser

依据Chen 等数值模拟采用的操作条件，将本文模型在同条件下的计算结果绘制在数值模拟结果图中，如图5(b)橙色实线所示，可以看到本文二次流模型计算得到的中心流线基本与数值模拟结果中边壁压力峰值点的连线相重合，表明本文对数值模拟结果中二次流中心位置的分析是合理的，同时也表明本文二次流中心流线模型具有较高的精度。值得注意的是，数值模拟仅计算了喷嘴以上0.2 m范围内的射流分布状况，相比于提升管进料影响区长度（一般在1～1.5 m[28]），模拟结果并不能反映进料段内的全部流场分布情况。然而，数值模拟需要耗费大量的算力和时间，如果对二次流产生发展的全周期过程进行数值模拟研究，所需的资源和时间将会难以估计。因此，针对二次流在提升管内的分布状况，使用本文模型进行预测是十分简便的。

3.2 向上30°进料模型计算结果与实验结果比较

图6为文献[29]对向上30°进料的提升管进料段区域不同喷嘴气速，不同轴向高度的射流相特征浓度（Cji）和颗粒相返混比（αi）的实验数据。

如图6(d)所示，在喷嘴以上0.375 m 处，三种不同喷嘴气速下，无量纲径向位置r/R=0.86 附近均存在一个射流特征浓度Cji的局部最低值，根据文献[29]的分析，此处应是二次流与射流主流的分界。那么该分界位置的左侧靠近边壁，即图6(d)中圈出的径向测点可以认为是靠近二次流中心位置的，且此处较高的颗粒相返混比也与二次流内高度返混[14]的特征一致。同时可以看到，Cji出现局部最低时，αi也在此区域迅速减小[如图6(d)粗箭头所指]，表明二次流内外存在着清晰的高返混与低返混边界。

随着轴向高度增加，在图6(c)可以看到，相比于0.375 m 截面，三个喷嘴气速下r/R=0.86 处Cji不再是最低值，反而在r/R=0.75处（图中圈出位置），出现一个局部射流特征浓度Cji和颗粒相返混比αi的峰值，可以认为此处是实验测得的二次流中心附近位置。轴向高度继续增加，在图6(b)和图6(a)截面中，沿径向射流特征浓度Cji不再出现局部峰值，且r/R=0.75之后的测点数值逐渐趋于稳定，说明二次流已经扩展分散，并向主流汇合。同样，图中粗箭头所指的高低返混边界位置，也随着高度增加而逐渐向提升管中心靠近，说明二次流内的高返混区域会逐渐扩大消失，同样表明二次流具有在边壁附近产生，随着高度增加而逐渐扩展，最终与主流汇合的发展趋势。因此，由实验结果表明，前文对二次流发展变化的理论模型是符合实际特点的。

图6 30°向上进料提升管进料段区域射流特征浓度与颗粒返混比Fig.6 Characteristic concentration of jets and backmixing ratio of particles in 30°upward feed riser

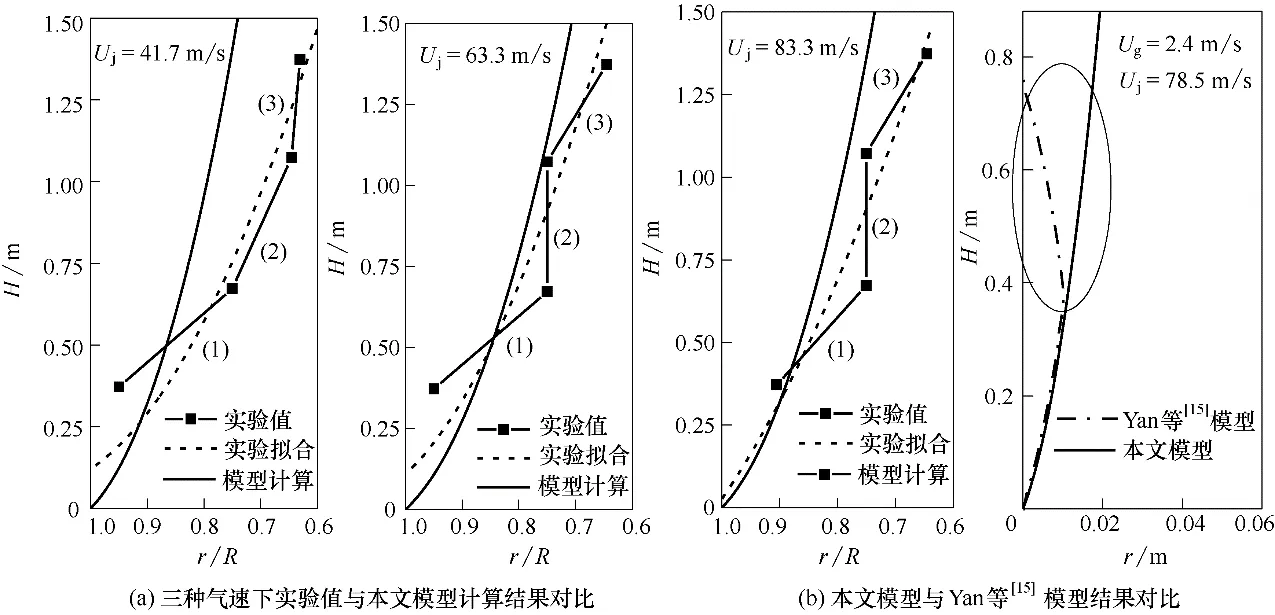
图7 本文模型与实验、文献[15]模型的对比Fig.7 Comparison of model in this paper with experimental data and Ref.[15]model

需要注意的是，由于实验难度较大，实验中径向测点布置较“稀疏”，图6 中圈出的二次流中心局部浓相位置实质是靠近二次流中心的一个区域，并不一定“恰好”是二次流的中心。

将图6中三种喷嘴气速下圈出的射流特征浓度位置分别按轴向高度布置，得到如图7(a)中折线图所示的二次流在不同喷嘴气速下沿轴向高度的变化趋势。可以看出，在每种喷嘴气速下，折线图中的(1)、(2)、(3)区 域 均 对 应 于 图4 颗 粒 相 受Kutta-Joukowski 力Fk作用时出现的三种情况。不同的是，图7(a)中折线图表示的射流相发展变化趋势正好与图4 的颗粒相运动趋势相反，表明前文给出的二次流与颗粒间相互作用的动量传递以及射流相受力分析是合理的。

利用数学手段对实验值进行回归拟合得到二次流发展回归曲线，如图7(a)中虚线所示。可以看出，本文模型计算得到的二次流中心流线[图7(a)中实线]与实验回归曲线在趋势上十分相似。由于模型计算的是二次流中心流线变化趋势，而实验的测点位置并不一定是二次流的中心，因此存在一定的偏差。

而Yan 等[15]提出的二次流中心流线模型，如图7(b)所示，其计算结果显示二次流会逐渐偏向边壁并与壁面相交（圈出位置），明显与图7(a)中实测结果不符。图7(b)中本文模型则较好地反映出二次流逐渐发展扩大的特征，相比而言更符合真实情况。

4 结 论

（1）利用Kutta-Joukowski 横向力理论，结合动量定理对提升管进料射流二次流产生、发展以及扩大的全周期过程给出了比较全面的理论解释，可以用于解释提升管进料混合段区域气固相流动行为。

（2）根据射流理论，通过引入Kutta-Joukowski力，提出了一种用于计算提升管内进料射流二次流分布的数学模型。结合其他研究人员的数值模拟与实验结果，验证了本文模型的可靠性，可以将模型用于预测不同操作条件下，提升管内射流二次流动的分布状况，可为提升管进料段结构的工业设计提供参考。

符 号 说 明

A——单连通域颗粒群面积，m2

b——射流微元体宽度，m

bj——喷嘴出口截面宽度，m

Cj——射流相特征浓度

Cn——气动阻力系数，通常取1～3

Fk——Kutta-Joukowski横向力，N

H——提升管轴向高度，m

J——旋涡强度，m2/s

M——偶极矩，m3/(h·m)

Q——体积流量，m3/h

qv——偶极子体积流量，m3/h

r/R——无量纲径向位置

U——射流进入提升管内的平均速度，m/s

Ug，ug——预提升气速，m/s

Uj，uj——喷嘴气速，m/s

Vs——颗粒与预提升气之间相对速度，m/s

x——理论模型中射流中心线横坐标，m

y——理论模型中射流中心线纵坐标，m

α——颗粒相返混比

β——射流主流与提升管壁夹角，(°)

Γ——速度环量，m2/s

γ——射流二次流与提升管壁夹角，(°)

δ——偶极子间距，m

ε——局部空隙率，%

ρg——预提升气密度，kg/m3

ρj——喷嘴射流密度，kg/m3

Ω——涡量，s-1

下角标

i——测量点