Explicit H1-Estimate for the Solution of the Lamé System with Mixed Boundary Conditions

AIT-AKLI Djameland MERAKEB Abdelkader

L2CSP,Mouloud Mammeri University Tizi-Ouzou,15000,Algeria.

Abstract.In this paper we consider the Lamé system on a polygonal convex domain with mixed boundary conditions of Dirichlet-Neumann type. An explicit L2 norm estimate for the gradient of the solution of this problem is established.This leads to an explicit bound of the H1 norm of this solution.Note that the obtained upper-bound is not optimal.

Key Words:Lamé system;Korn’s inequality;Poincare’s inequality;inequality of trace;explicit estimates.

1 Introduction

Let Ω be a bounded open connected subset of R2.The static equilibrium of a deformable structure occupying Ω is governed by the Lamé linear elasto-static system,see[1]. In this paper,we restrict the study to a convex domain Ω whose boundary has a polygonal shape that possesm+1 edges withm≥2.We denoteits boundary andd(Ω)its diameter.Moreover,we assume that all the edges Γihave strictly positive measure.The system under consideration is given by

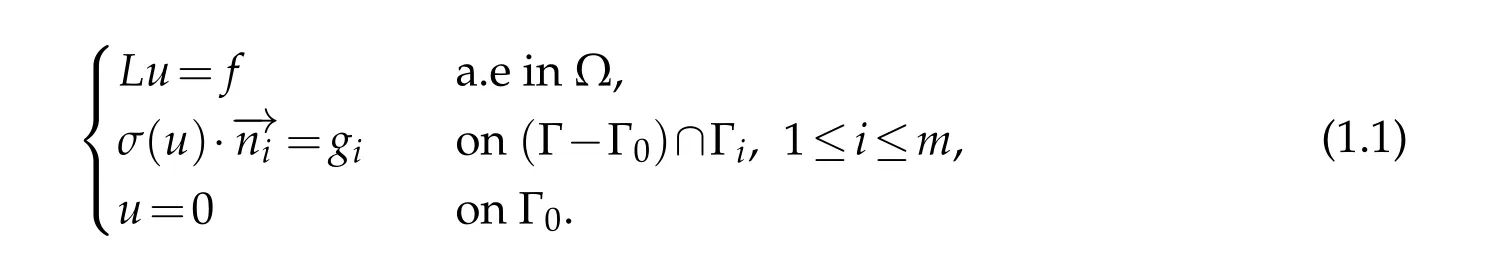
We need to assume that the edges Γiwhich form the boundary Γ fulfill a condition similar to assumption(H2)in([2],Theorem 2.3).Actually,for our purpose,a stronger condition is needed and it is formulated in(1.5)below.The vector functionu=(u1,u2)satisfying the system(1.8)describes a displacement in the plane.In this model we impose a homogeneous Dirichlet condition on Γ0and a Neumann condition on the remaining part of the boundary. The equality on the boundary is understood in the sense of the trace.We denoteLthe Lamé operator defined by

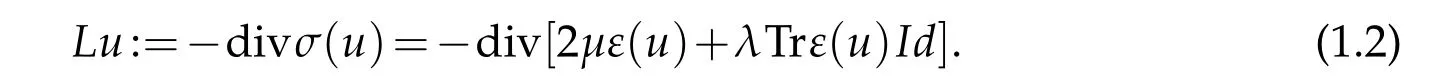
We assume the data functionsfandgat the right hand sides to satisfyf ∈[L2(Ω)]2andThe vectorrepresents the outside normal to Γi.We writeμandλthe Lamé’s coefficients.We place ourselves in the isotropic framework,the deformation tensorεis defined by

The weak form of problem(1.1)is(see[1,3]):Findu∈Vsuch that∀v∈V

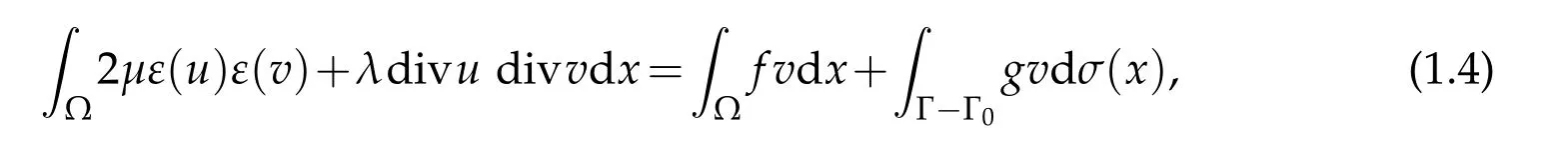
where

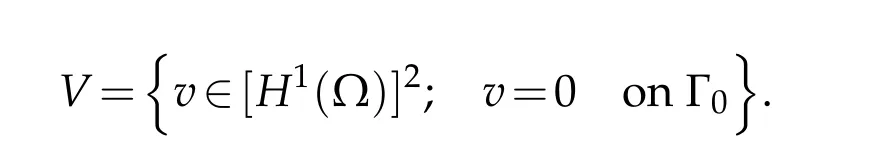
The existence and uniqueness issue of the solution of(1.4)inVis classic,(see[3]).

If we denoteθthe interior angle between the edges Γjand Γk,0≤j,k≤msuch thatand if we denoteγthe interior angle between the Neumann part of the boundary ΓN:=Γ-Γ0and the Dirichlet part of the boundary ΓD:=Γ0,then we impose

The reason behind this assumption on the boundary is to get a better regularity of the solution of the weak problem(1.4).Precisely in that case we have,following([2],Theorem 2.3)stated at the bottom of page 330,for some positiveι＞0,which implies in particular,using the appropriate Sobolev embedding and since Ω is a locally Lipschitz domain,see part II of([4],Theorem 4.12,page 85),thati.e.uisι)-holder continuous.One should notice that condition(1.5)are met since the domain considered in our case is convex.Let us denote

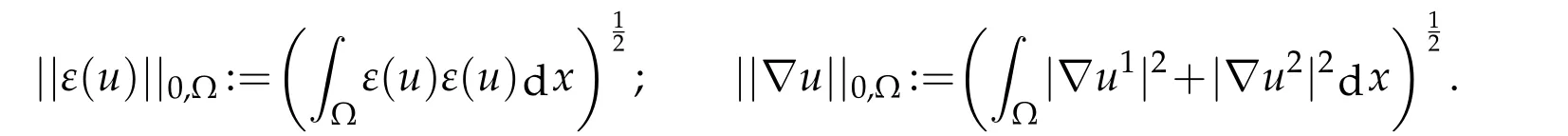
By using the second Korn inequality,see[5],the trace and the Poincaré’s inequalities,one easily gets from(1.4)the following estimate

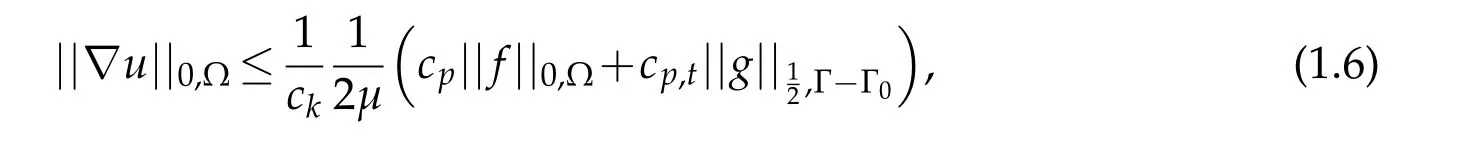
wherecp,tis a constant that depends of Poincaré constant and the constant of trace inequality.ckis the constant of the Korn’s inequality.Note that the value of the constantckandcp,tappearing in(1.6)are unknown and can not be explicitly lower-bounded or upper-bounded in the general case.We propose to determine explicitly these constants.The main result of this work is stated in the following theorem:

Theorem 1.1.The unique weak solution u of(1.4)on the convex polygonal domainΩadmits the explicit upper bound

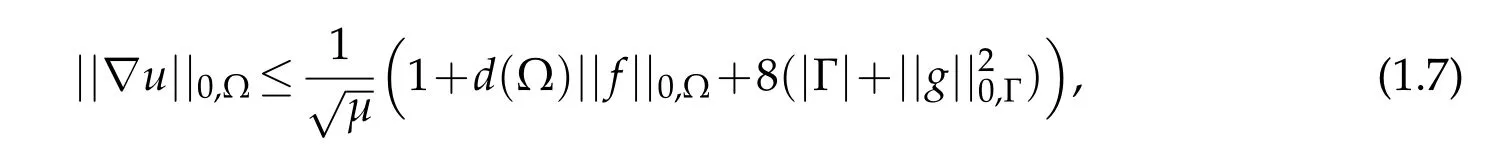
where d(Ω)represent the diameter ofΩand|Γ|the measure of the boundary ofΩ.

Estimate(1.7)is similar to estimate(1.6)in the sense that the constants appearing there are the same.Before demonstrating this theorem,it is useful to go through some remarks and results.These auxiliary results are needed in order to adequately get a decomposition of the solution of the main problem,which belongs toH1(Ω),into functions that are still inDenotexi,for 1≤i≤m,the vertex of the polygon that connects Γi-1with Γiandx0the one that connects Γmto Γ0.Define the auxiliary functionuϵ ∈H1(Ω)as the unique solution to the following Dirichlet problem

whereis the trace on the boundary Γ of the function

Forthe functionφϵis defined by

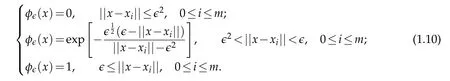
Let us denote

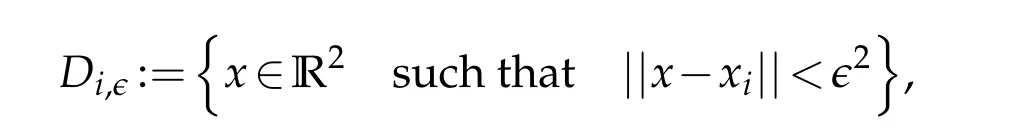
where||x-xi||stands for the Euclidean norm of the vectorx-xi.We easily see thatφϵ ∈consequently,there will be no jump when passing to the distributional derivative and thus∇uϵ ∈L2(Ω),and by using the poincaré inequality,we infer thatuϵ ∈H1(Ω).It is shown,using Lebesgue’s dominated convergence theorem for instance,that

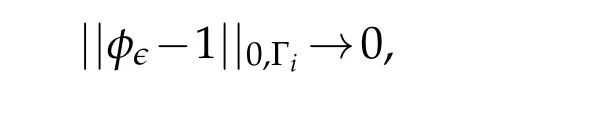
i.e.we have convergence inL2along the edge Γi.The functionsφϵare identically zero on a small neighborhood of the respective vertices of the polygon.

In the sequel,we denoteuϵthe vector-valued function

2 Weak problem for uϵ and approximation results

First of all,we construct the weak problem verified by the approximating functionuϵ.With the approximating displacementuϵ∈Vis associated the approximating stress tensor

sinceLuϵ=divσϵ=f,thenFor a fixedϵ,by density of the regular functions in the spaceH(div)(Ω),there existssuch thatin[H(div)(Ω)]2×2.This means

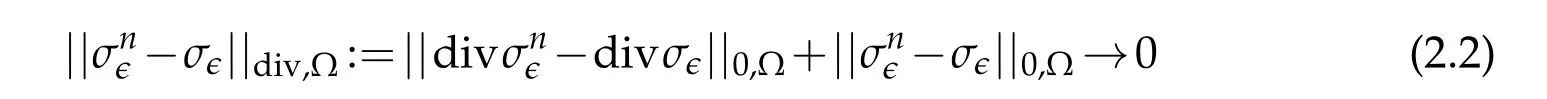
whenn →∞.We posethen integrating by part against a test functionv ∈yields the following

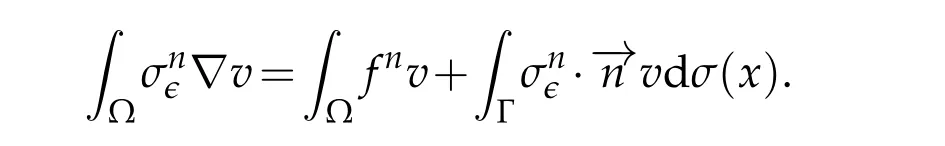
Passing to the limit innusing(2.2),we find

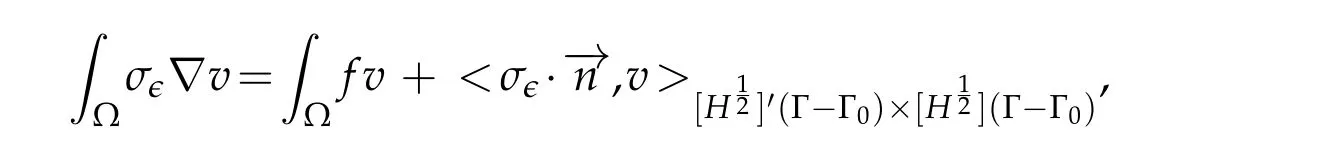
whereis the image of the normal componentσϵby the trace

operator on Γ. Since,following theorem 1 established in[8],is a dense subset ofV ⊂H1(Ω),then,according to the definition(1.3)and the expression(2.1),the functionuϵsatisfy

this is the weak problem satisfied by the approximating functionuϵ.

Let us recall,(see[6]),that thenorm in one dimension on Γiis defined by

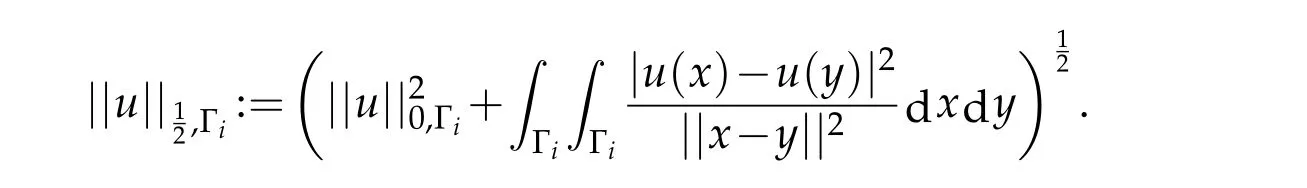
Remark 2.1.For any sufficiently smallϵ＞0,it is possible to cover Ω with a collection of open setssuch that for eachj,is either empty or equals one of the following subsets:for somei,0≤i≤m-1

and fori=m

One should well remark that,following its definition,the functionφϵ-1 has nullsemi norm onthis fact justify the writing of the last term in estimate(2.4).So,using the definition and symmetry ofφϵ,we get for all 0≤i≤m

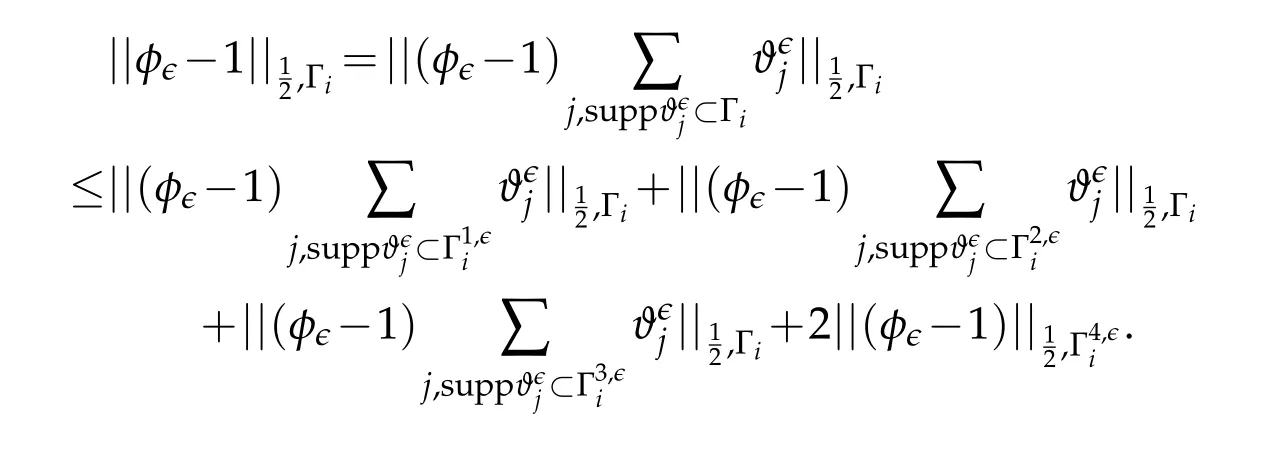
Thus,

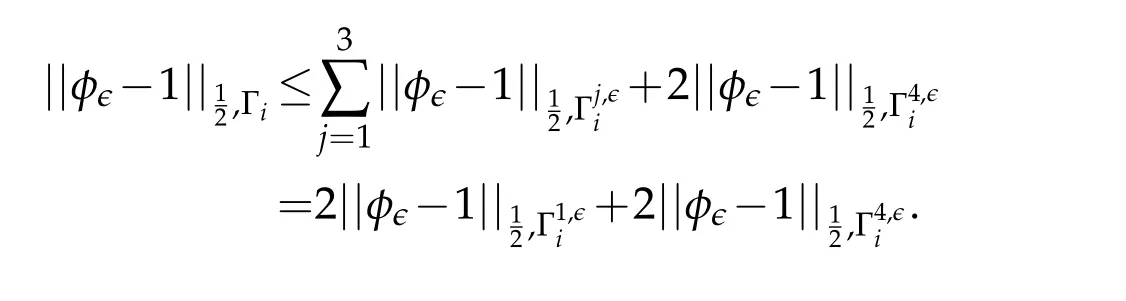
Thus we have

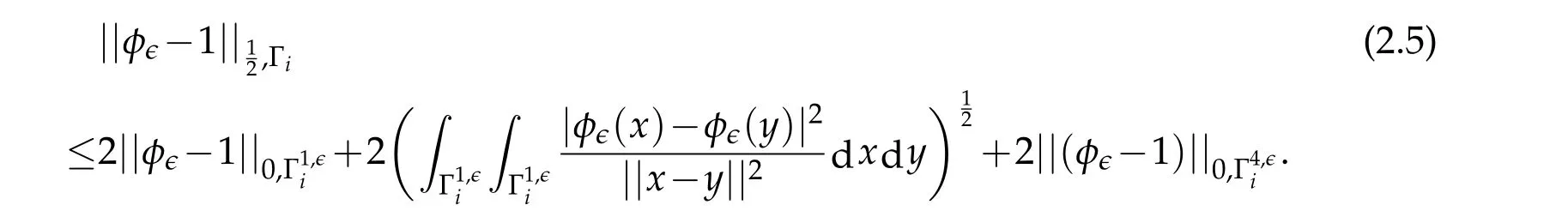
Lemma 2.1.The functions φϵ admit the following limits

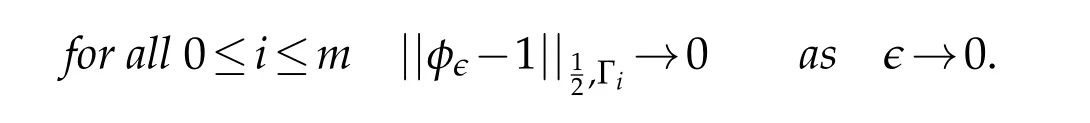
Proof.If we choose the vertex pointxias the origin of the R2-orthonormal coordinate system such that Γiis supported by the positive halfx-axis then the abscisses ofx ∈

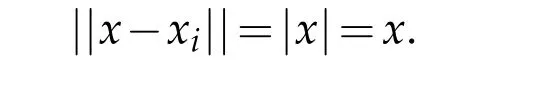
The-semi-norm ofφϵon Γiwrites

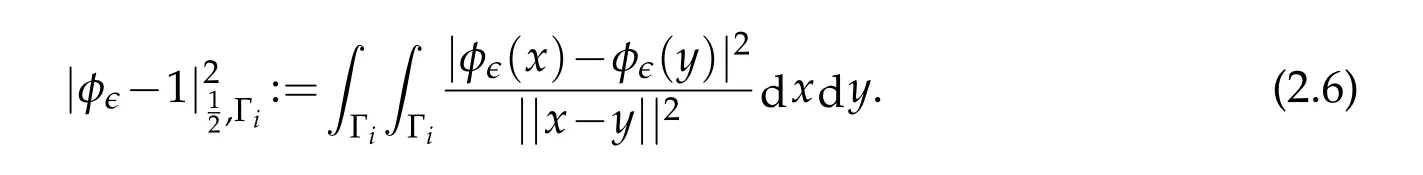
It yields by using the definition ofφϵ

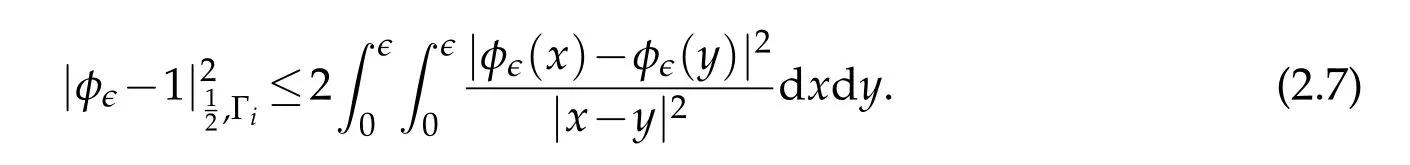
Consider the decomposition of(2.7)into four partial double integrals

this is obvious.

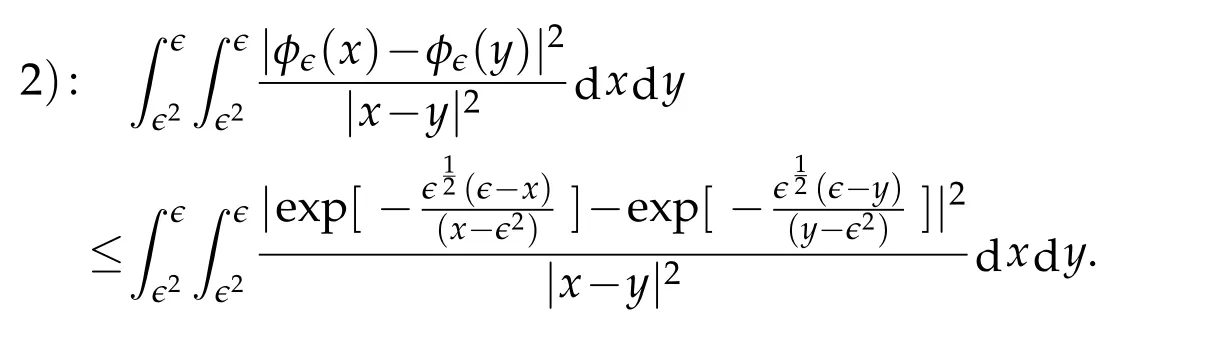
fact thatx→F′(x)is increasing on,that

On the other hand

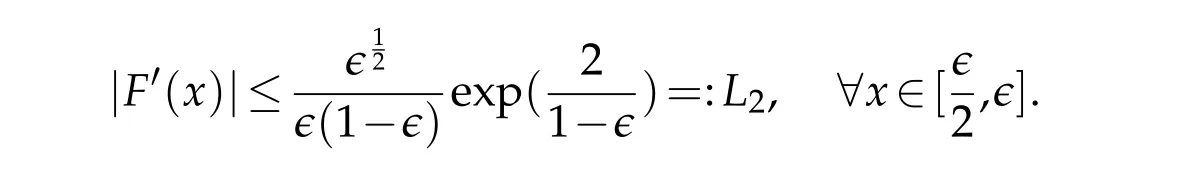
Therefore we conclude that

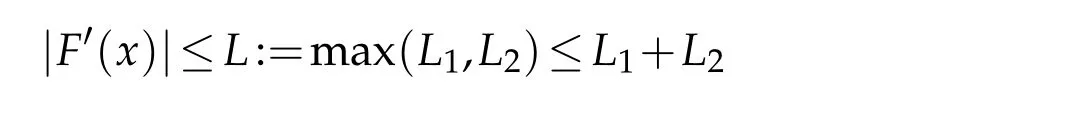
for allx∈[ϵ2,ϵ].This yields

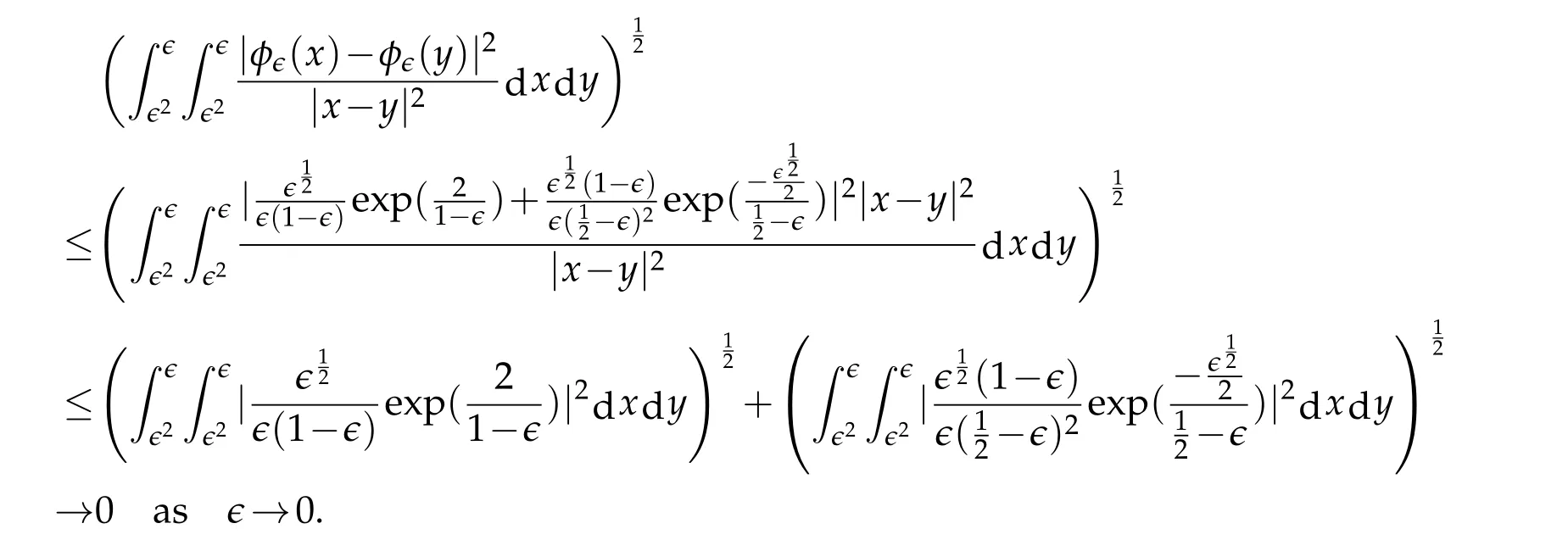
One more integral is

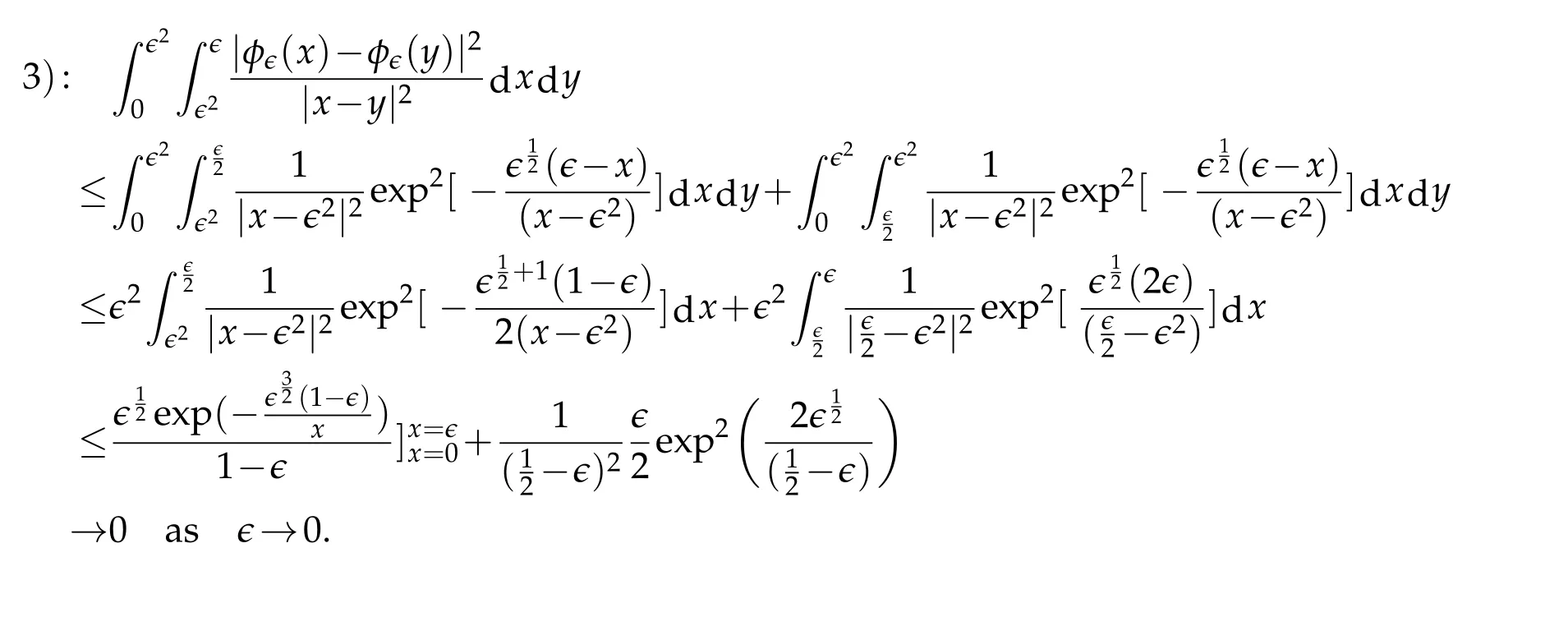
Here we used the properties of the exponential function and elementary majorizations.This final integral is

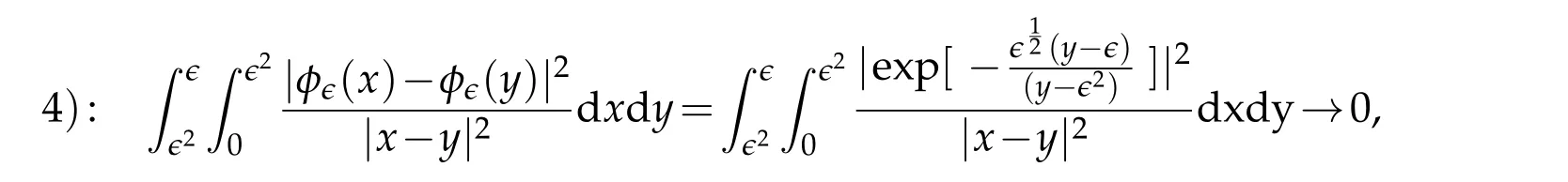
proceed in the same way as for 3).

Combining these four integrals on one hand and using the facts:

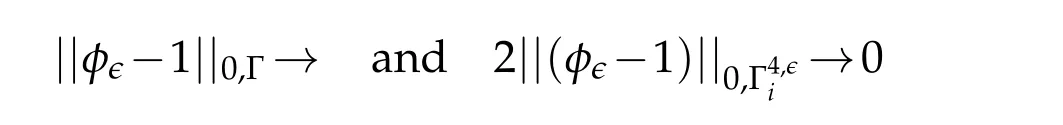
for all 0≤i≤mon the other hand yield,using(2.5),the result of Lemma 2.1.Consequently,using(2.4)yields also

This completes the proof of the lemma.

Sinceuis-Hölder continuous and thus uniformly continuous on Ω,the result of Lemma 2.1 implies

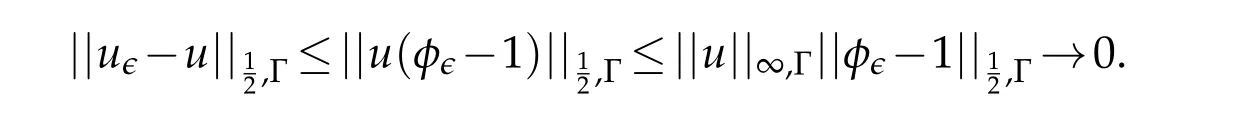
One can now prove the following approximation lemma:

Lemma 2.2.The function uϵ defined by(1.8)and the distribution gϵ appearing in problem(2.3)satisfy respectively the following limits

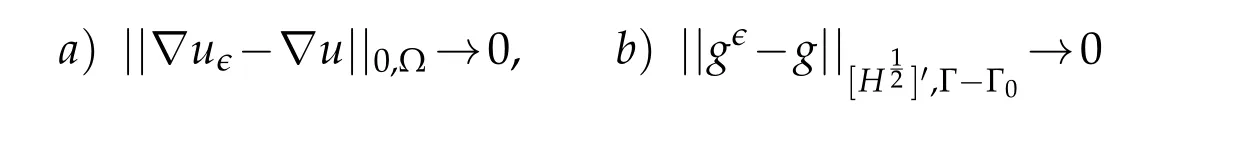
as ϵ→0.

Proof.a)let us consider the following problem

Consider the linear operatorGthat associates to eachthe corresponding unique solutionuof problem(2.8),

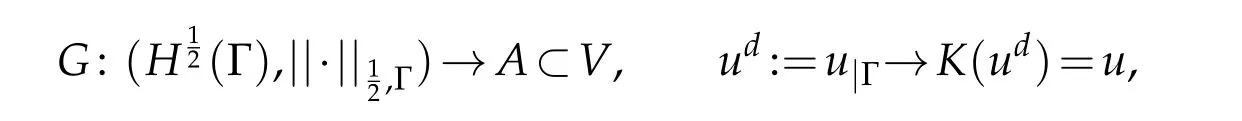
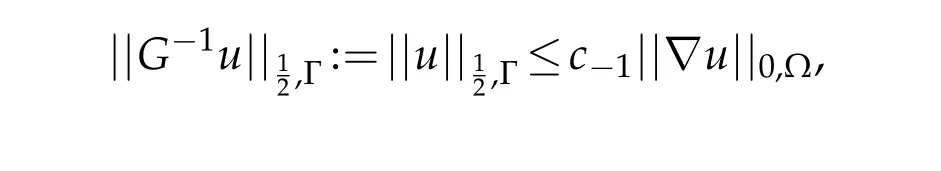
this implies the continuity of the linear bijective operatorG-1.According to the Banach isomorphism theorem,the operatorGis continuous,this means that there existsc ＞0 such that for allu∈Awe have

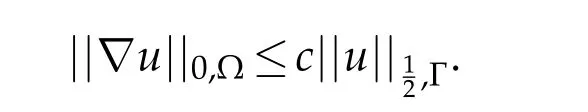
Thus,sinceL(u-uϵ)=0,using the limit established in Lemma 2.1

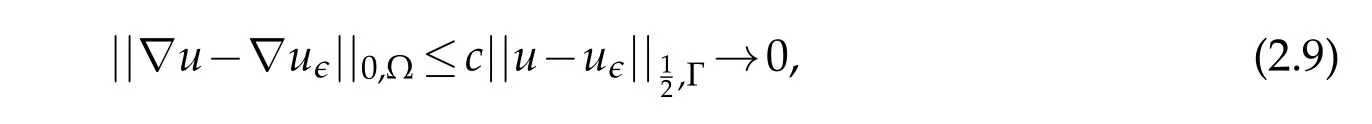
this provesa).

b)We make the same reasoning as fora).Givenletw ∈Vbe the unique solution of

for allv∈V.Choosingv=w,there existsc′＞0 such that

LetKbe the operator that associates to each datathe solution function

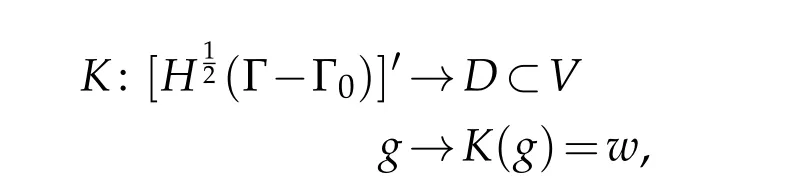
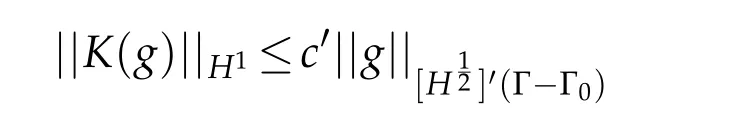
i.e.Kis continuous.Then,according to Banach’s isomorphism theorem,we deduce thatsuch that

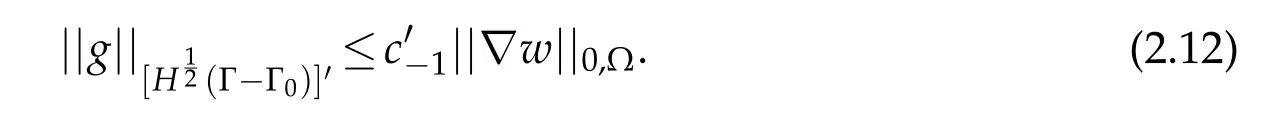
Rewriting(1.4)withthen subtracting(1.4)and(2.3)member-to-member,one find thatu-uϵsatisfy:∀v∈V,

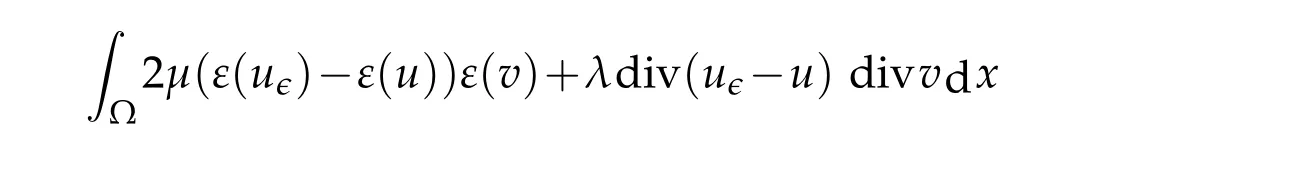
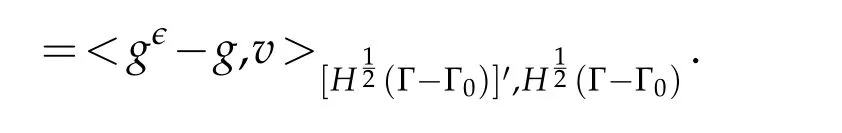
Applying(2.12)tow=uϵ-uwe get:

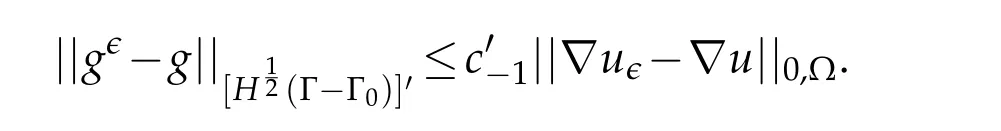
Considering(2.9),we inferb).

Remark 2.2.A consequence of the previous lemma:for arbitrary smallβ＞0,there existsϵ1＞0 such that∀ϵ,0＜ϵ＜ϵ1,we have

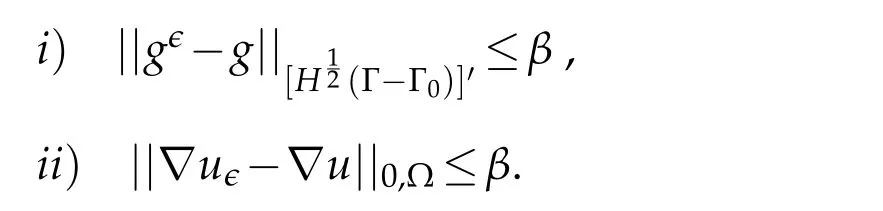
iii) Since,by assumption,then,using the continuity of the canonical embedding

3 Auxiliary lemmas

Letϵ1be such as defined in remark(2.2).For the rest of the paper,we fixϵ,0＜ϵ＜ϵ1.

Before presenting a proof of the main result,we intend to state two auxiliary lemmas.These lemmas are established using,principally,([7],Theorem 2.1).In order to apply this later result,assumption 1.2 in that same paper need to be met.Our polygonal domain satisfy very well that assumption.

These lemmas,Lemmas 3.1 and 3.2 below,convey the essential idea in the demonstration of the main theorem 1.1.We begin with approximating the solutionuϵof problem(1.8)by a smooth function vanishing on an adequate part of the boundary Γ.Then the idea is to carry out a particular decomposition,alluded to in the introduction,of this approximating function. This key idea is illustrated in the following example. Considerv∈Vto be the solution of a problem similar to(1.8),e.g.,

We assume that the trace ofvon the boundary vanish on an open neighborhood of the vertices of Ω.Set

Let us decompose this problem into two other problems

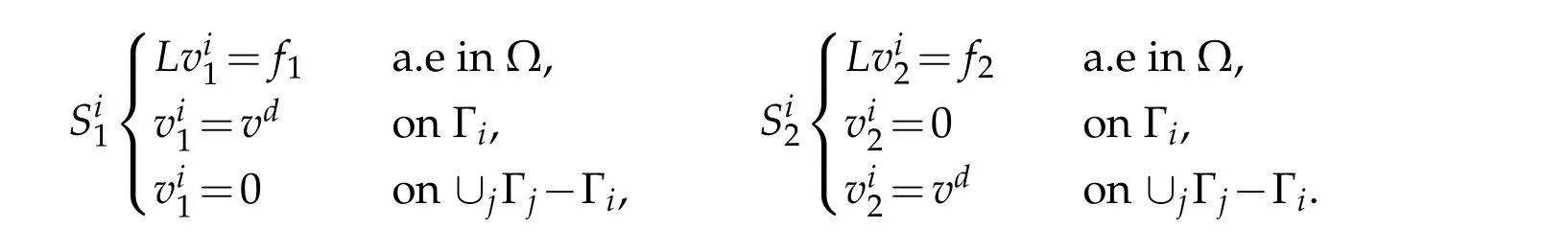
Provided that the problems are well posed,the functionsandare well defined.On the other hand,it is easy to see that the fact=von Γidoes not generally imply thaton Γi.So the idea is to find a decomposition that makes such a property to be fulfilled.i.e.such thatcan be approximated by a functionand,at the same time,such thatis an approximation ofon Γiin the sense of trace.An adequate use of Theorem 2.1 proved in[7]can make this decomposition possible.

Using([8],Theorem 1),we can findsuch that for eachp,vanishes on the same part of Γ where doesuϵand such that

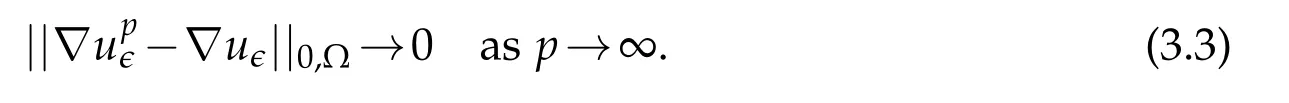
If we denote

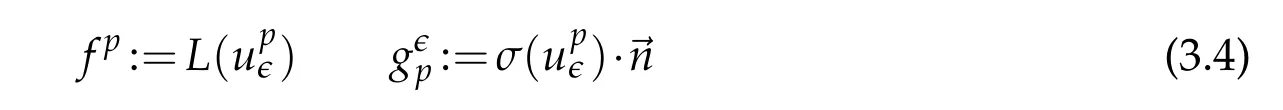
then,a particular consequence of(3.3)is:we can fixpsuch that

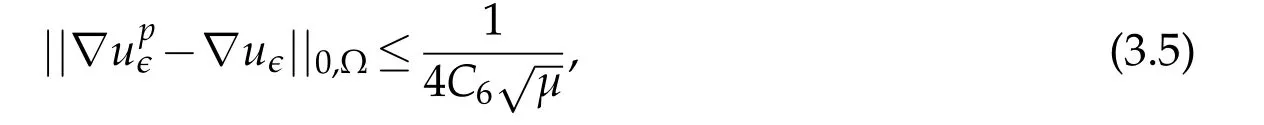
whereC6is the continuity constant of the operatorG′-1defined as follows.LetG′be the operator that associates to each datathe solutionvof

i.e.

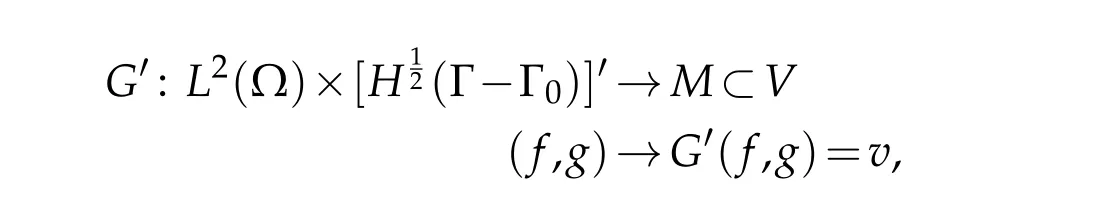
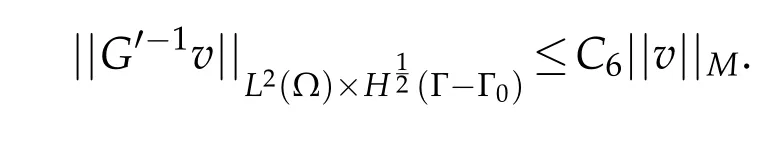
Thus by using(3.5)we obtain,withand given an arbitrary smallβ＞0

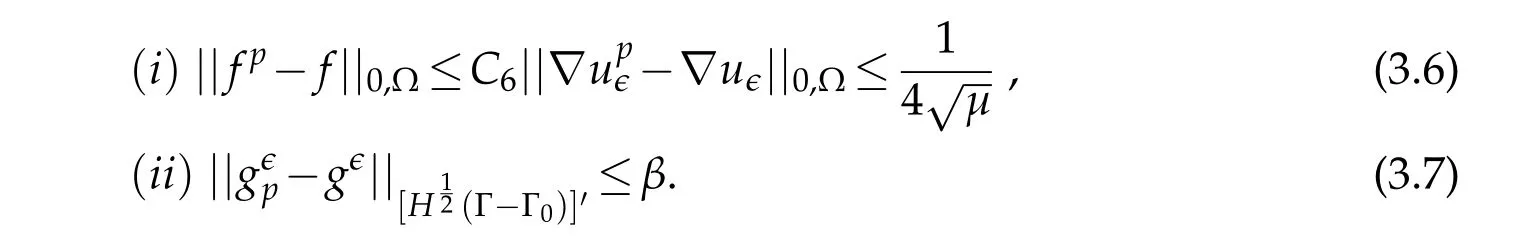
We fix,for the rest of the paper,pfor which(3.5)-(3.7)are fulfilled.

Lemma 3.1.Let δ0be an arbitrary small number.There exists two functions u1and u2such that

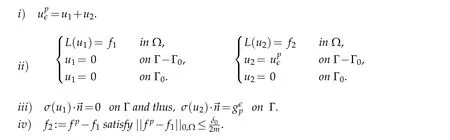
Proof.Letδ0＞0 be an arbitrary small number.Consider the decomposition

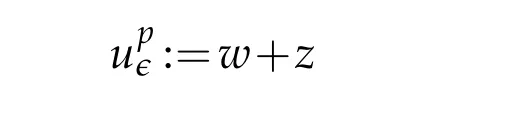
wherewandzare respectively the solutions of the following problems

Observe thatσ(w)·→ndoes not necessary equal zero and thusσ(z)·→ndoes not necessary equalg.Nevertheless,by density,there is functionssuch that

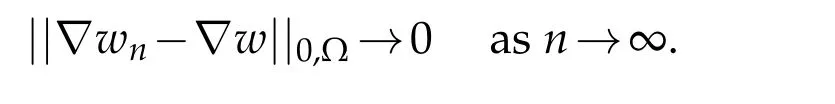
One should note that,following the definition of compactly supported functions in Ω,σ(wn)=0 on∂Ω for alln.

Using the same argument as in the proof of Lemma 2.2(Banach theorem),and for the fixed homogeneous Dirichlet boundary condition,there existsC0＞0 depending merely on the domain Ω such that

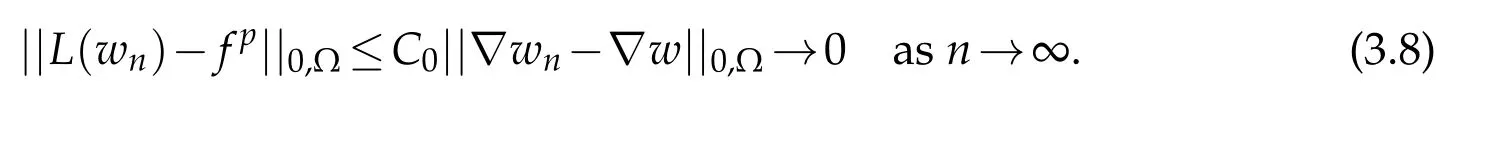
Thus,there exists an elementw*in{wn}n∈Nthat satisfy the estimate

Decomposew:=w*+w2wherew2is a solutions of

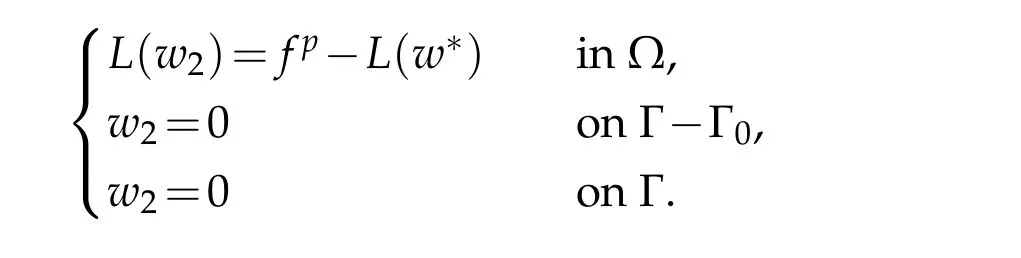
One should remark that

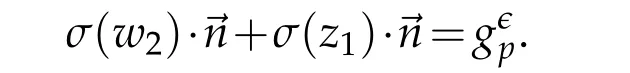
Indeed,Pose

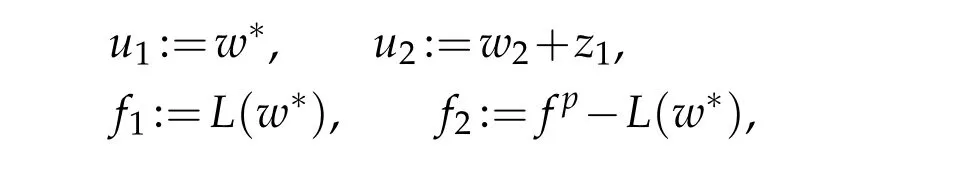
this concludes the lemma.

It should be pointed out that we repeatedly apply the essential argument in Lemma 2.2,namely the Banach isomorphism theorem,in order to obtain estimates for the inverse of some operators.On the other hand,although the functionsu1andu2depends onϵwe have removed the indexϵfor clarity of presentation.

Lemma 3.2.Let Ei be the subspace of V defined by(3.2).Let u1,u2be such as defined in Lemma3.1.Given δ1,δ2＞0arbitrary small numbers,there exists m functions u2,i ∈Ei,1≤i ≤m,such that

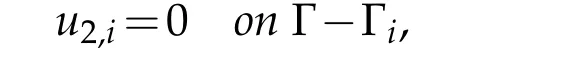
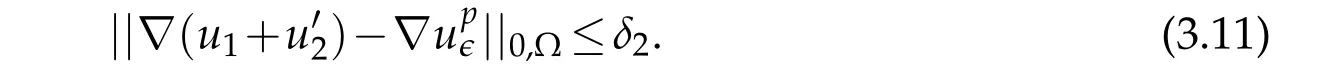
The construction of the functionu2,ithat is presented in the proof of Lemma 3.2 below shows that for alli,the functionsu2,ivanish not only on Γ but also onNi∩∂Ω,whereNi ⊂R2is an open neighborhood of Γi.The proof is done in two main steps.In the first one,we construct the functionsu2,iand in the second step we prove that these functions actually satisfy estimates(3.10)-(3.11).

Proof.Letδ1,δ2be arbitrary small numbers.The functionsu2,iwill be defined by introducing the intermediate functionsandVirespectively in subsectionsa),b),c)andd).As we define these functions,we demonstrate some estimates that will be used to derive(3.10)-(3.11)in the second step.

Step 1:Fixi,1≤i≤m.Consider the decomposition

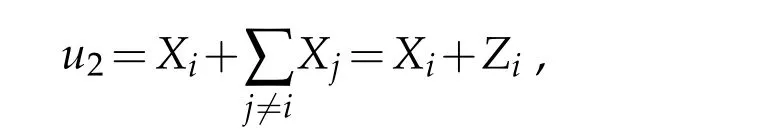
whereXi ∈EiandZiare the solutions of

One should notice that these two problems are well posed,this can be seen by considering the regularity ofon the boundary and the fact thatvanish identically on a neighborhood of the the vertices. Since Ω is a Lipschitz domain,it posses theW1,2-Sobolev extension property.

a) According to([7,Theorem 2.1])see Appendix A at the end,there existssuch that we have

whereδ3＞0 is an adequately chosen real number.A consequence of(h2)is:

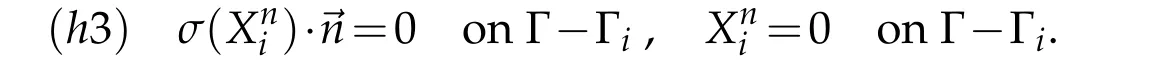
Furthermore,with the homogeneous Dirichlet condition on Γ-Γibeing fixed in the problemP1and in the problem solved bythen,using the Banach theorem,there existsC1＞0 such that

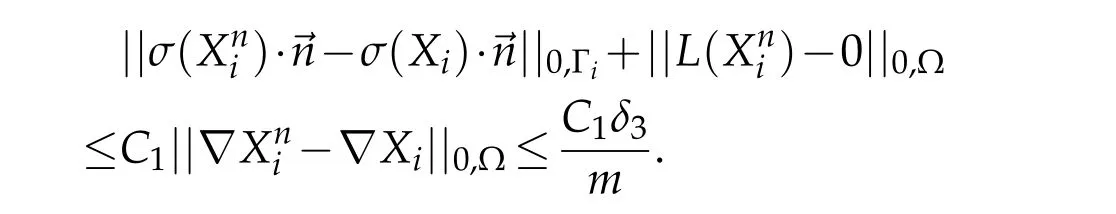
We chooseδ3in assumption(h1)such that

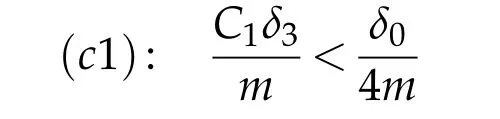
whereδ0is a positive real number whose choice will be precised later(see condition(c4)below).Fixn1such thatsatisfy

or equivalently,

for the same reasons as for(P1)andproblems(P2)andare well posed.Considering(h3)and(3.13),the functionsatisfy

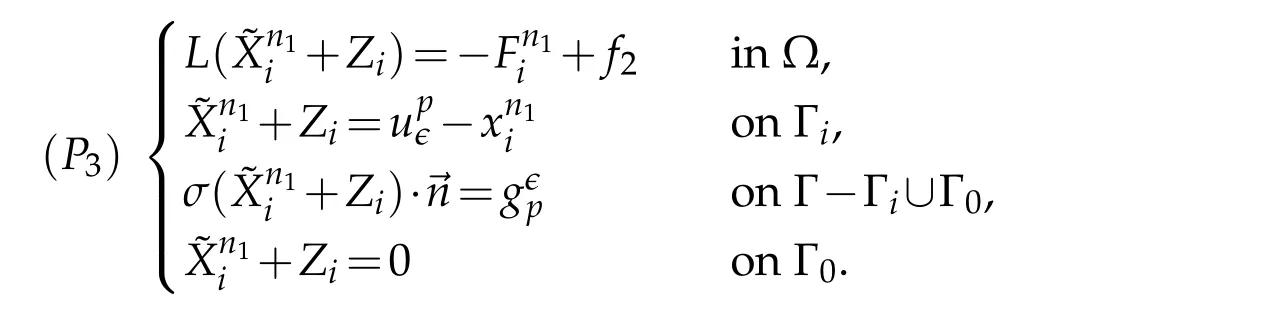
b) LetYibe the function defined by

thanks to assumption(1.5),this problem is well posed.There exists a trace constantctsuch that,using(h1),we have

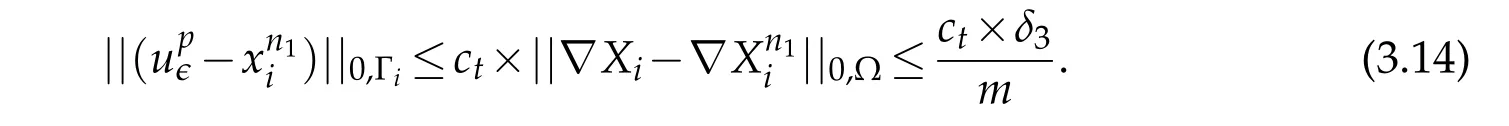
For the fixedand the homogeneous Dirichlet condition on Γ0in problems(P3)and(P4),and by using an argument similar to that in part(a)of the proof of lemma(2.2)(Banach theorem),there exists a constantC3＞0 such that

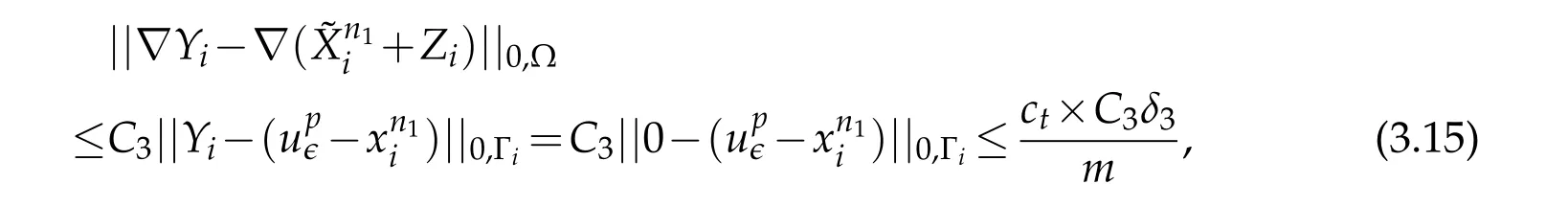
and by using the trace inequality again we have

Considering(3.13)and(h3),we easily see thaton Γ-Γi;and thus,estimates(3.15)and(3.16)become respectively

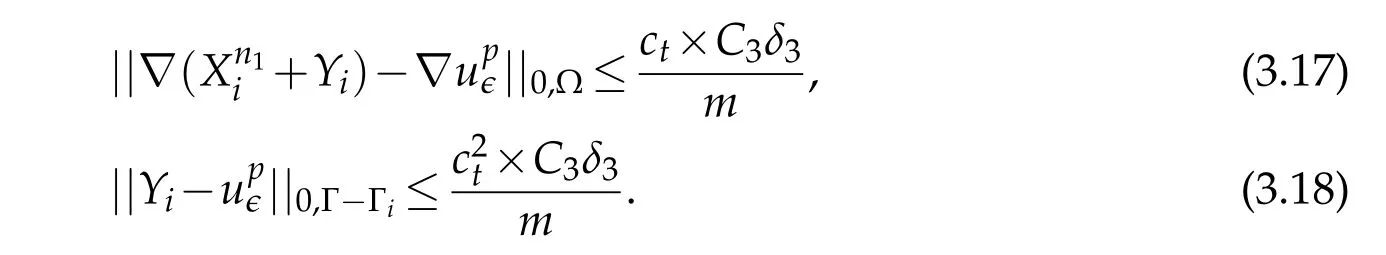
On the other hand,sinceYi=0 on Γithen,using the result(Theorem 2.1,[7]see Appendix A at the end),there existssuch that

whereis an adequately chosen real number,thus

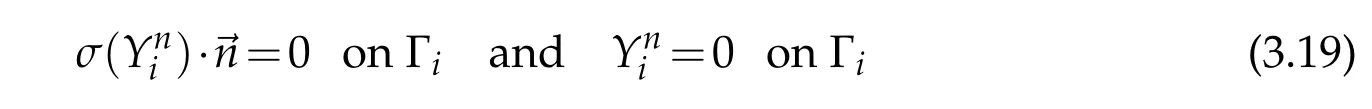
for the homogeneous Dirichlet condition on Γi∪Γ0for problem(P4)and the problem solved byand using Banach theorem,there existssuch that

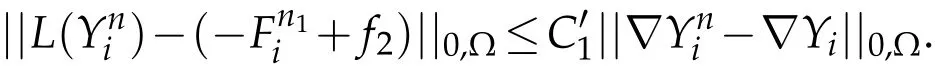
We choosein assumption(h4)such that

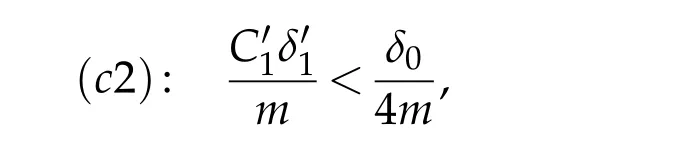
whereδ0is as defined in Lemma 3.1 i.e.need to satisfy condition(c4)below.Fixn2＞n1such that

satisfy

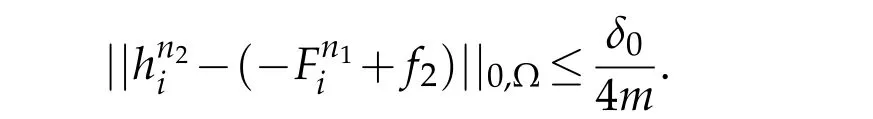
Consequently,considering(iv)of Lemmas 3.1 and 3.2 and(3.12),we have

c) Denotewe have

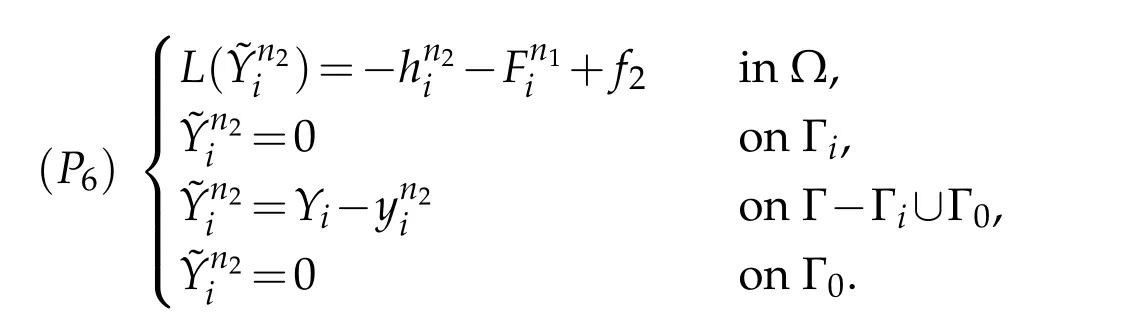
Rewriting estimate(3.17)gives

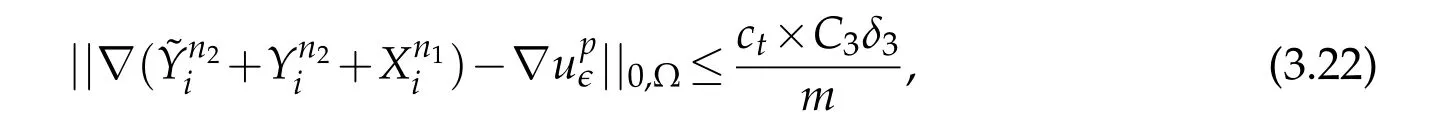
and denote

d) LetVi ∈Eibe the function defined by

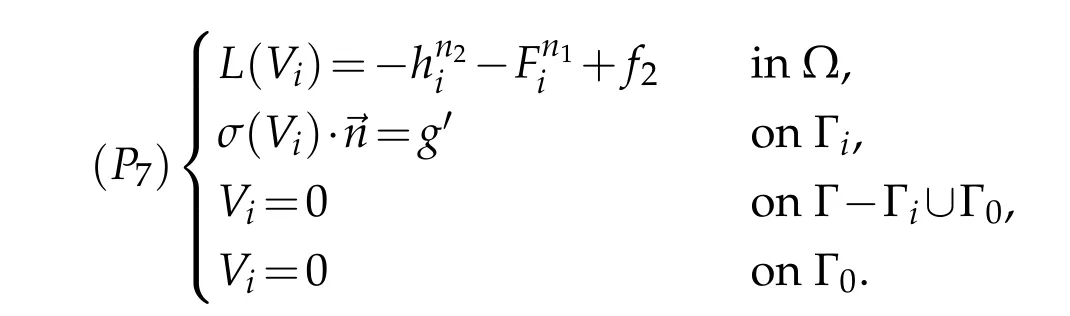
Set

Step 2:The functionsu2,iare the unique solutions of

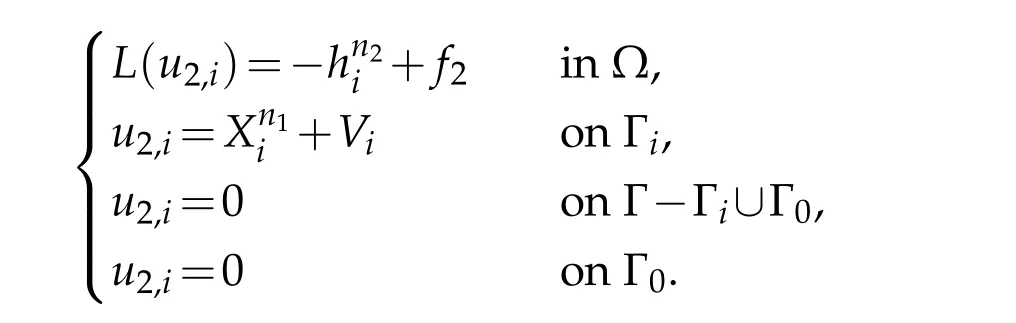
Using the estimates established in step 1,we are ready to prove(3.10)-(3.11).

Proof of estimate(3.10):Sinceon Γi,then we have for

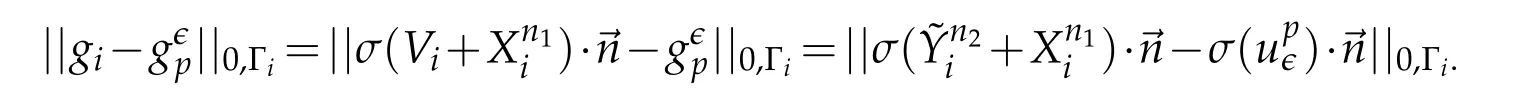
Using(3.19)givesc

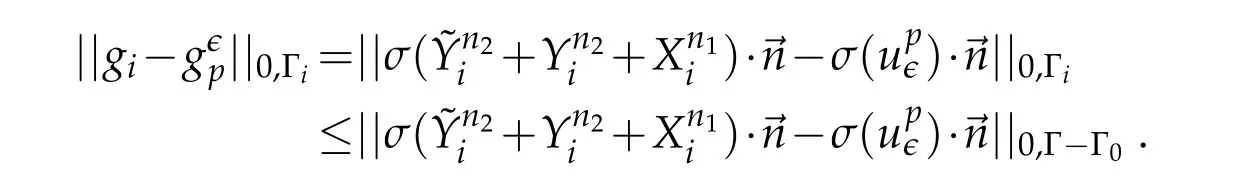
For the fixed homogeneous Dirichlet condition on Γ0,and according to the Banach isomorphism theorem,there exists a constantC2＞0 depending merely on Ω such that,using(3.22)and since we have

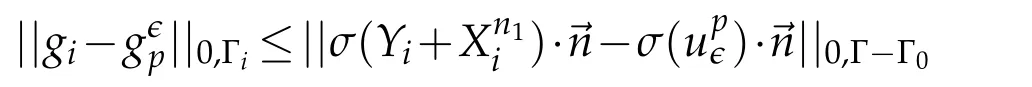
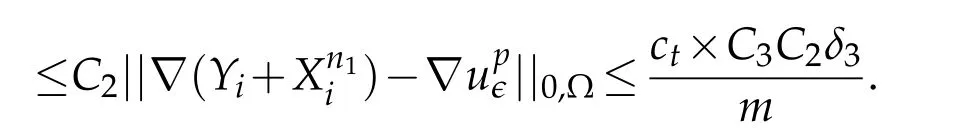
Ifδ3also fulfill condition

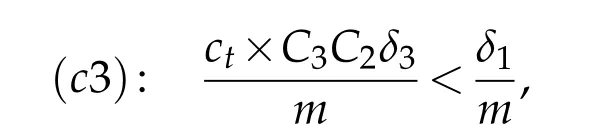
whereδ1is the arbitrary small number assumed at the beginning of the proof then,estimate(3.10)is proved.

In order to prove estimate(3.11),we need to estimate the trace ofon Γi.

1) Firstly remark,by using(h3),that

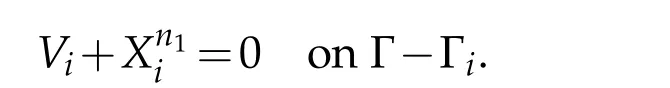
2) For the fixedand the homogeneous Dirichlet condition on Γ0in problems(P6)and(P7),the Banach isomorphism theorem ensures the existence of a constantC4＞0 depending merely on Ω such that

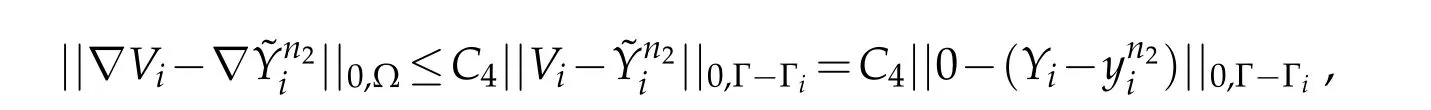
hence,considering(h4)and using trace inequality,we have

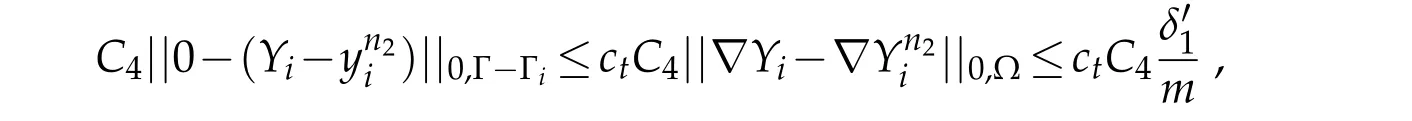
thus,

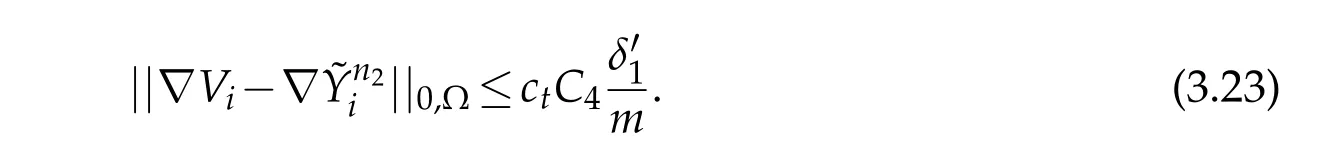
Using trace inequality and(3.23)we obtain

Estimates(3.14)and(3.24)imply

Proof of estimate(3.11):Writewhereζ′andη′are respectively the solutions of

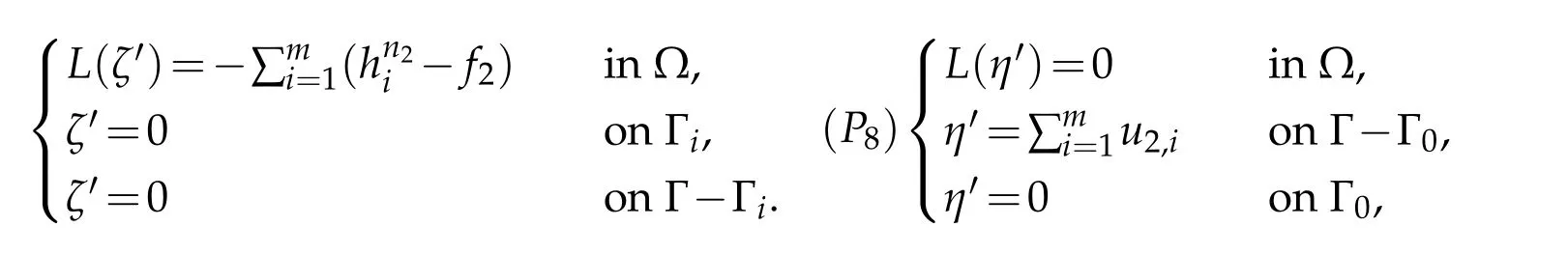
and writeu2=ζ+ηwhereζandηare the solutions of

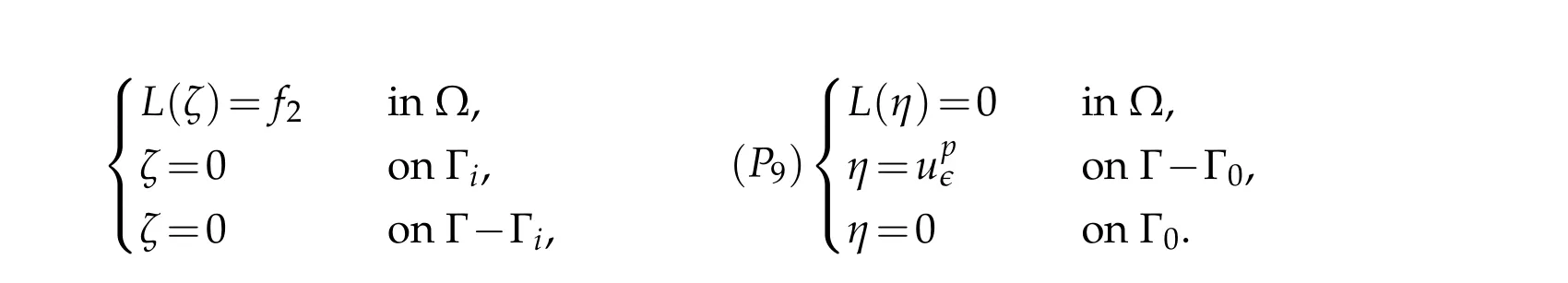
If we denoteckthe constant in the Korn inequality then the weak form of the problem solved byζ-ζ′yields

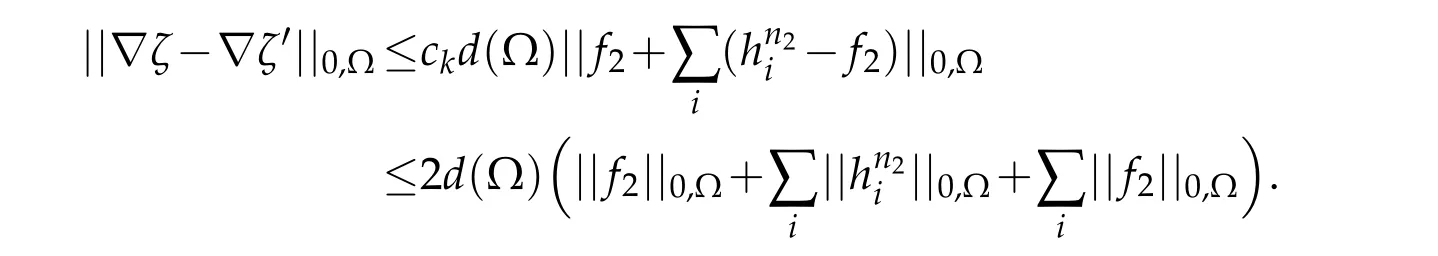
Using(iv)of Lemmas 3.1 and(3.21),we have

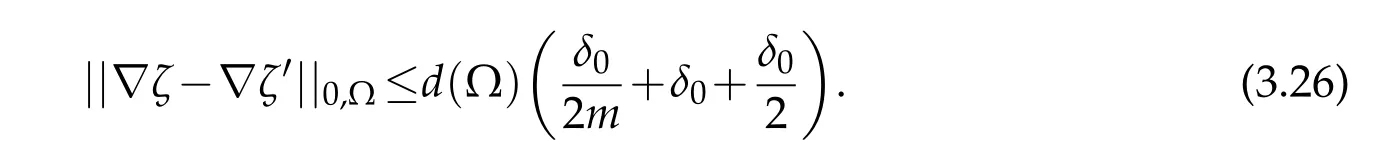
On the other hand,the Banach isomorphism theorem ensures,for the null source term and the Dirichlet homogeneous condition on Γ0in problems(P8)and(P9),that there exists a constantC5＞0 such that

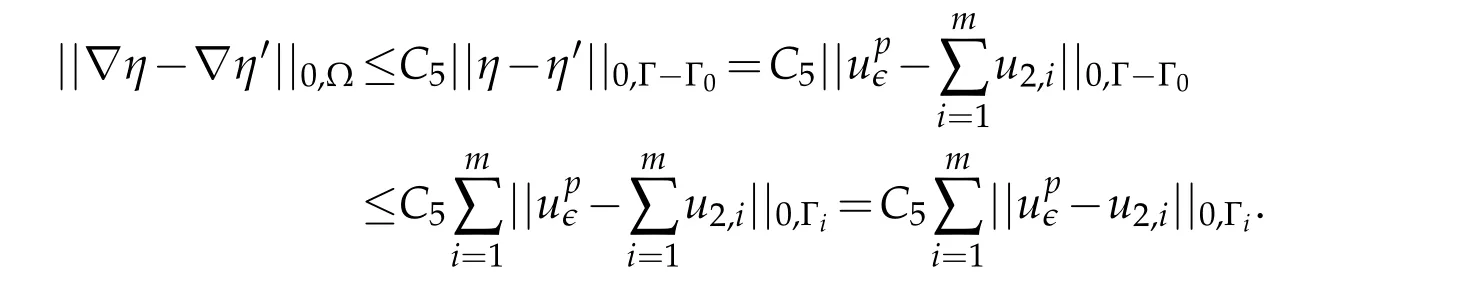
Applying estimate(3.25)with

Combining(3.26)and(3.27),we obtain using triangular inequality

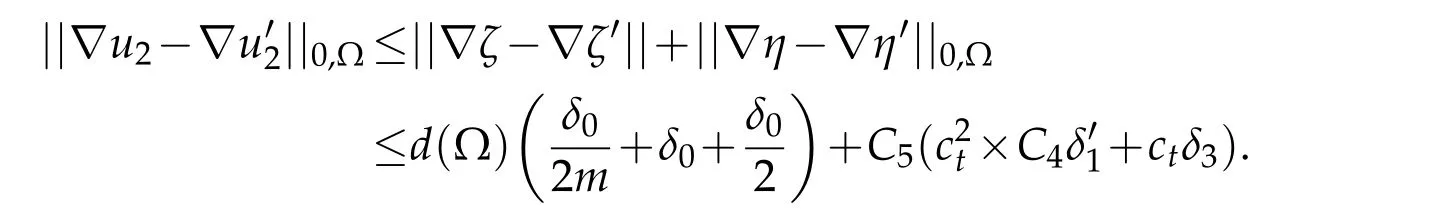
Finally,ifδ0,δ3andare subject to fulfill the condition

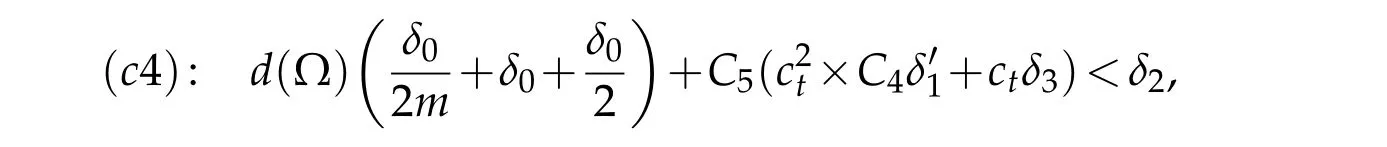
whereδ2is the arbitrary small number assumed at the beginning of the proof then,

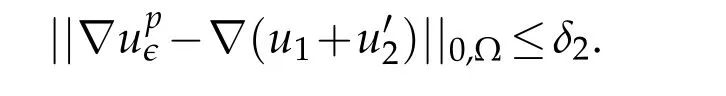
This proves(3.28).

Remark 3.1.1) Letsuch as defined in(3.4),we can easily show that

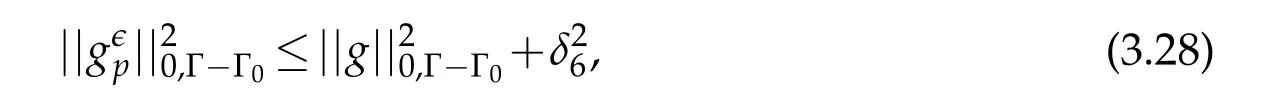
whereδ6is an arbitrary small positive real number.Indeed,write using triangular inequality

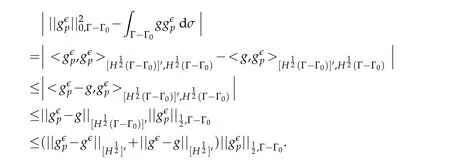
Since,following estimate(ii)of(3.7),converges intogϵi.e.weakly inhence,there existsC′＞0 such thatfor allp∈N.Thus,

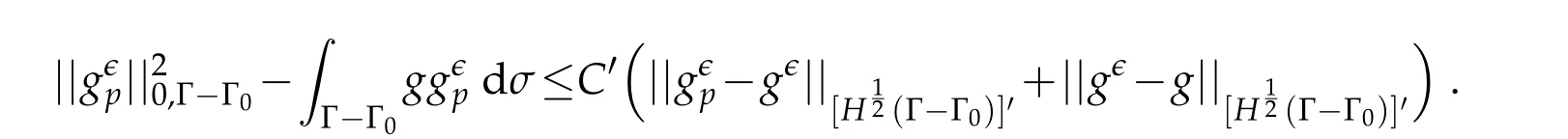
Using(i)of Remark 2.2 and estimates(ii)of(3.7)and for an adequate choice ofβ,the parameterspandϵcan be chosen such that

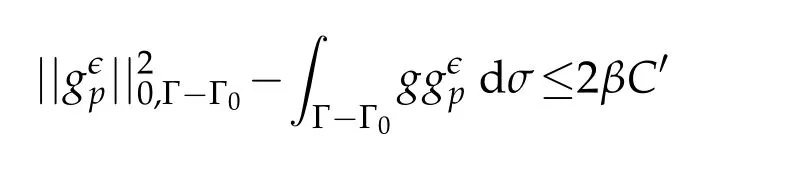
and thus,Cauchy-Schwarz yields

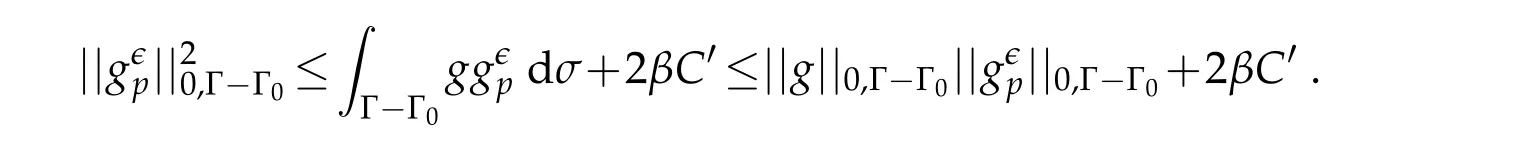
Young inequality on the other hand gives us

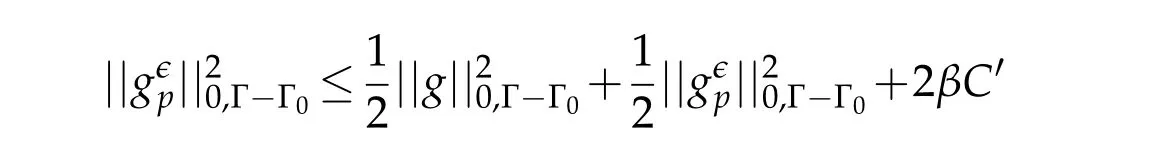
and hence,there existspsuch thatsatisfy

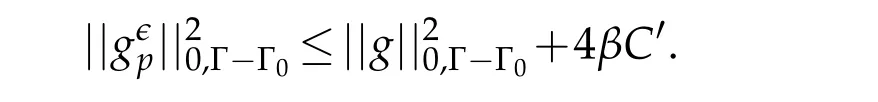
PoseSince,following(i)of Remark 2.2 and(3.7),βis arbitrary small,then the same holds withδ6.

2) On the other hand,ifu2,iandare respectively such as defined in Lemma 3.2 and(3.20)then

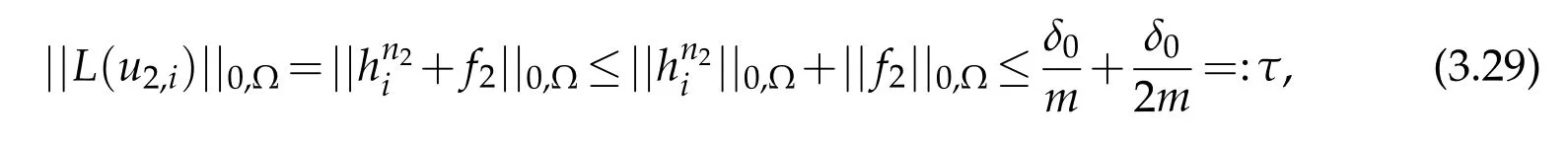
whereδ0is arbitrary small and satisfy(c4)and thus,τis also arbitrary small.

We introduce some useful lemmas,which will play important roles in the proof of Theorem 1.1.

3.1 Extension of the functions u2,i

Since we are looking for explicit estimates,we should use Poincaré,trace and Korn’s inequalities relatively to suitable geometric configurations i.e.for which they are explicitly formulated.The configuration that best fits our polygonal convex domain Ω is the half-plane R2+containing the domain Ω for Korn’s inequality,the squareSdwith edge’s length equal tod(Ω)for the Poincaré inequality and with edge Γifor the trace inequality.These squares are taken to be subsets of the half-plane containing Ω.Thus we determine these constants thanks to results available for this type of domains.The need to consider the functions in and outside the domain Ω suggests to extend by zero the functionsu2,ioutside the convex domain Ω. The definition of the functionsu2,iis adapted to make such an extension.

Letu2,ibe such as defined in Lemma 3.2.We consider fori,1≤i ≤m,the extension by zero ofu2,ifrom the convex domain Ω to the half-plane R2+containing Ω such that Γi ⊂∂R2+.

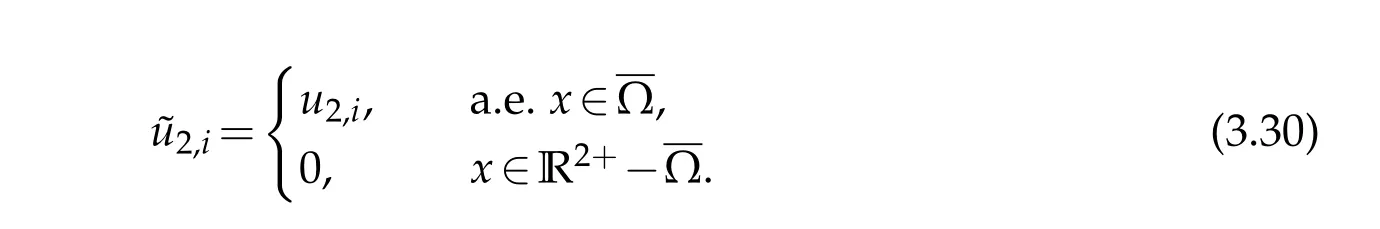
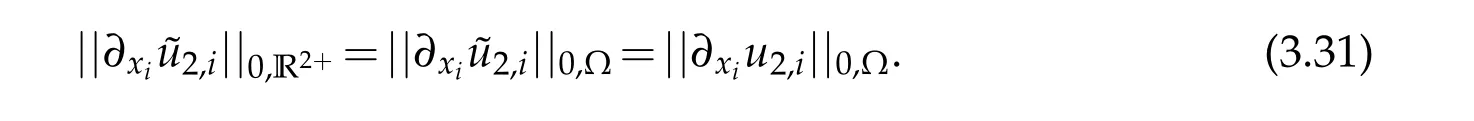
One can easily see that the resulting extend functionsare still in the Sobolev spaceH1(R2+).Indeed,thanks the definition of these function,there will be no jump when passing to the distributional derivative.

The following inequalities are established for the extendedH1regular functions defined on a square containing the convex polygonal domain Ω.

3.2 Explicit constant in the Poincaré inequality

We show in the following lemma that the functionu2,i ∈Eisatisfy the Poincaré inequality for which we determine explicitly the constant.

Lemma 3.3.For all i,0≤i≤m,the function u2,i satisfy:

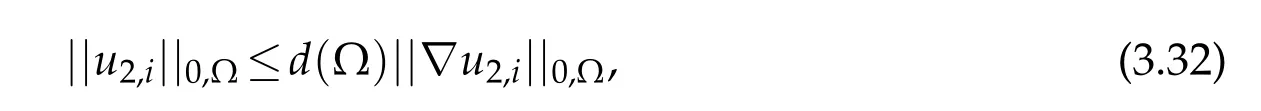
the constant d(Ω)means the diameter ofΩ.

Proof.We establish Poincaré inequality for one of the two components=1,2,the same estimate hold with the other.Noteabcdthe squareSd,with edge’s length equal tod(Ω)and subset of the half-plane containing Ω,such thata=(a1,a2),b=(b1,b2),c=(c1,c2)andd=(d1,d2)and such that

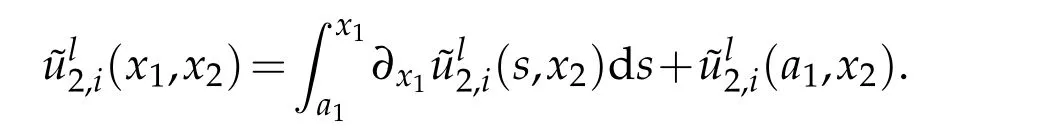
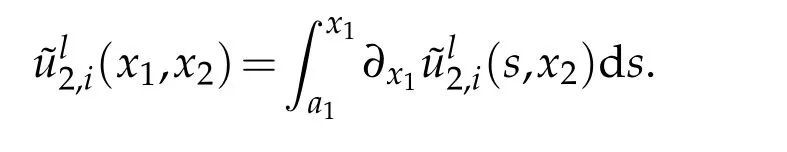
Using Cauchy-Schwarz inequality∀(x1,x2)∈[a1,d1]×[a2,b2]

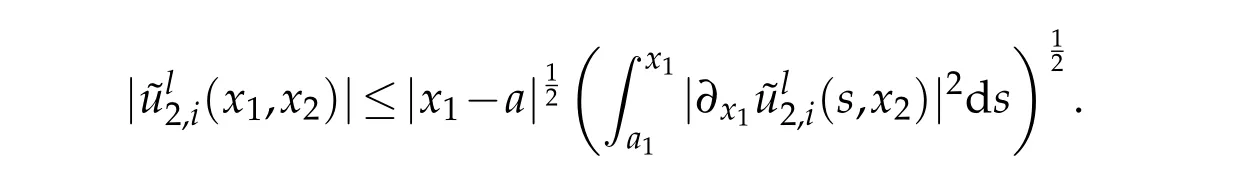
Taking the square of the two hand sides of this inequality and using the fact|x1-a|≤d(Ω):∀(x1,x2)∈[a1,d1]×[a2,b2]yields

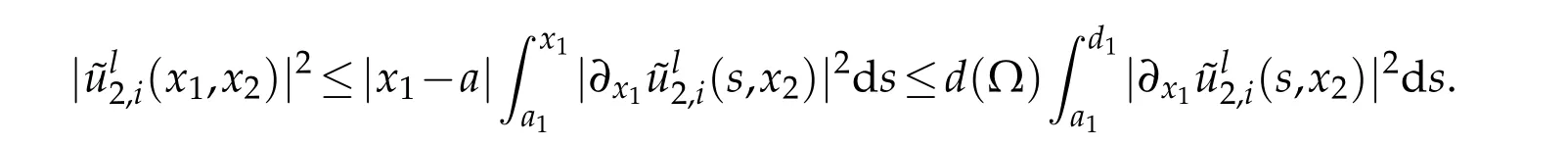
Integrating onSdwith respect to the variablesx1andx2:

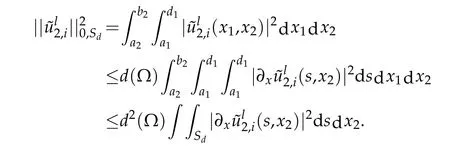
According to definition(3.30)and by considering(3.31)we get

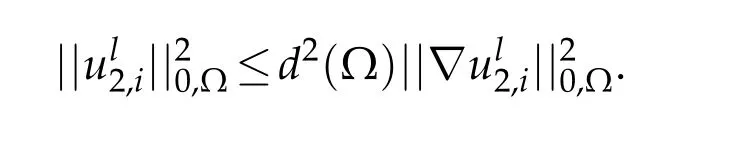
We infer that

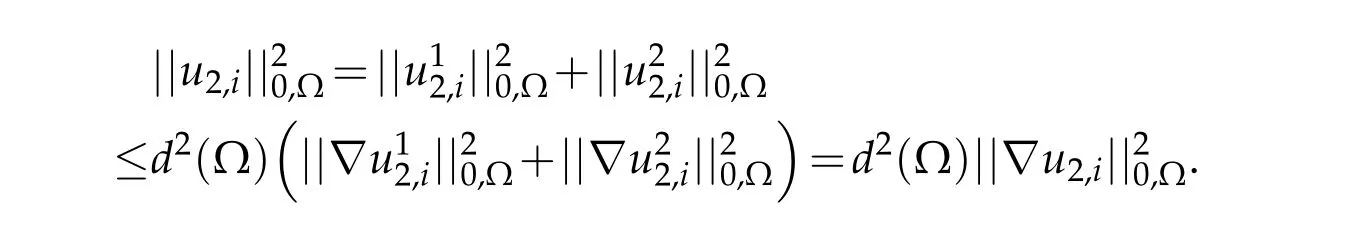
This completes the proof of the lemma.

3.3 Explicit bound for the trace of u2,i on Γi

Using mainly the inequality of Poincaré stated in Lemma 3.3 and the trace inequality foru2,ion the edge Γiof a the parallelogramSΓi,see([9,Lemma 4.2])as well as([10,Remark 3.3],)and the reference therein,one establishes an explicit bound for the trace of the functionu2,ion Γi.

Lemma 3.4.For all i,the function u2,i defined in Lemma3.2satisfy:

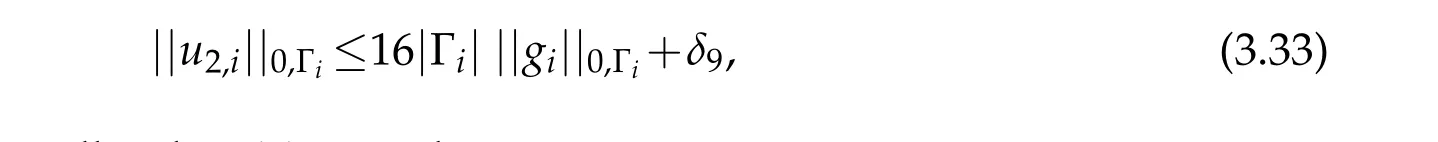
where δ9is an arbitrary small real positive number.

Proof.Letbe defined on the squareSΓiwith edge Γisuch thatSΓiis a subset of the halfplane R2+containing Ω.One should notice thatis not necessarily zero on∂SΓi-Γi.Let us write

this decomposition is made similarly to that presented in Lemma 3.2,i.e.,such that on one hand

and on the other hand,α,ϱvanish respectively on∂SΓi-Γi,Γi.We prove(3.33)for the trace of the functionα,the same estimate holds for the trace ofu2,isinceαandu2,icoincide on Γi.Decomposeα:=α1+α2in the following way

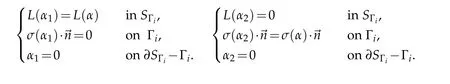
Applying the inequality of trace on the boundary Γiof the the squareSΓi,which is a parallelogram,see([9],Lemma 4.2),it yields for bothk=1,2

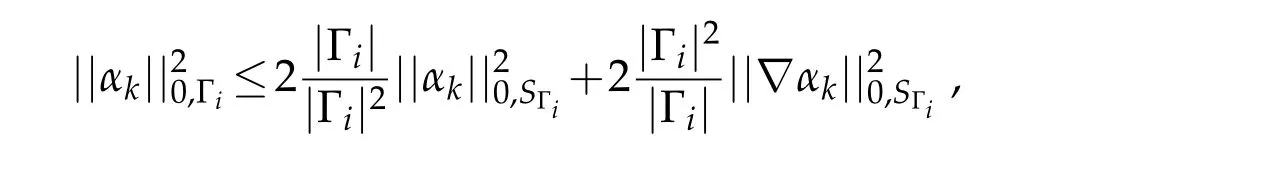
simplifying,

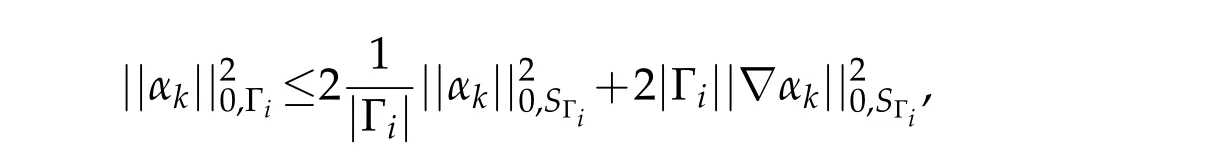
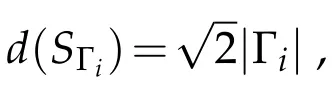
Applying Korn’s inequality for the extended functiondefined on the half-plane R2+containingfor which case Korn constant equals,estimate(3.35)becomes

Sinceα1andα2satisfy respectively

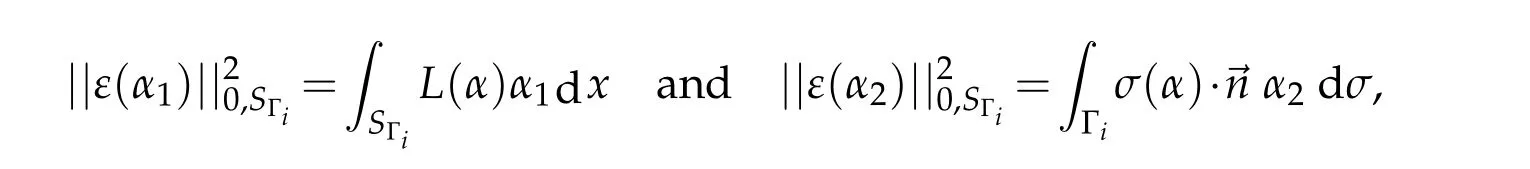
then,using Cauchy-Schwarz,this leads to estimates

Using these last estimates,(3.36)becomes

Using(3.29)and assumption(3.34),we can findδ5andδ6small enough such that

for alli.Hence,combining these two estimates,we obtain

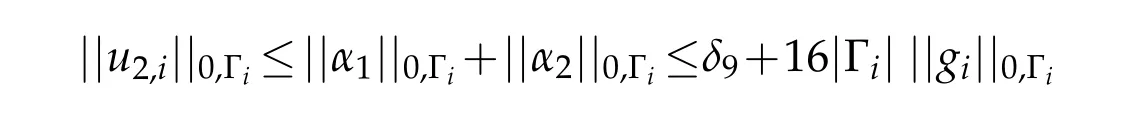
withδ9=δ5+δ6arbitrary small.

4 Proof of Theorem 1.1

We are ready now to present a proof of the main theorem.It uses,principally,Lemmas 3.1 and 3.2.

Proof.Step 1:Letu1be as defined in Lemma 3.1,it is easy to check that it satisfies

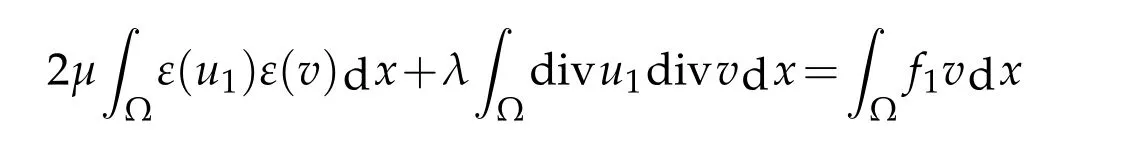
for allChoosev=u1and use Cauchy-Schwarz inequality

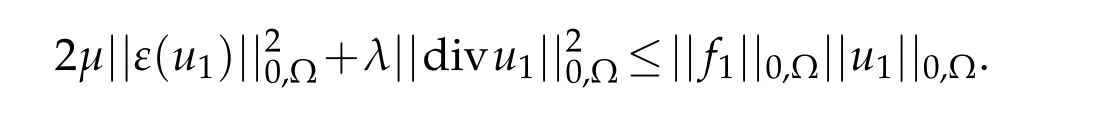
Using Korn’s inequality relatively to the case of homogeneous Dirichlet condition on one hand,and Poincaré inequality on the other hand,yield

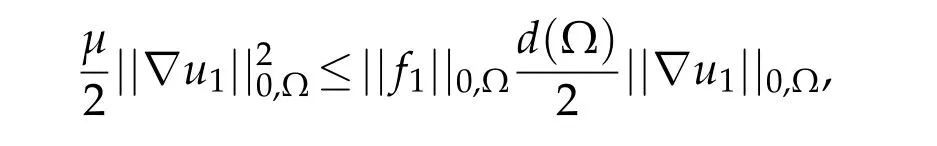
using(iv)of Lemma 3.1,we obtain

Fixi,1≤i≤m.Letu2,ibe such as defined in Lemma 3.2,it is easy to check thatu2,isatisfies

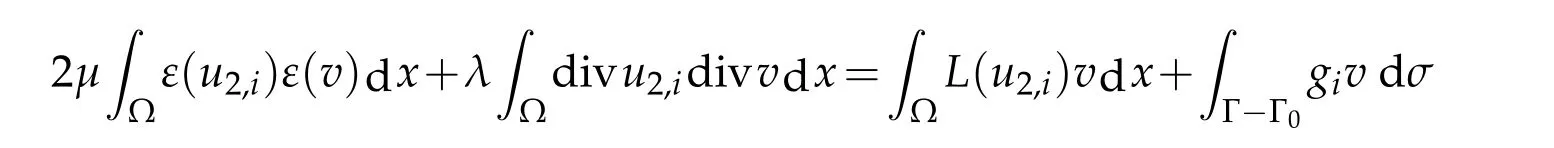
for allv∈V.Choosev=u2,iand use Cauchy-Schwarz to obtain

using estimate(3.32)

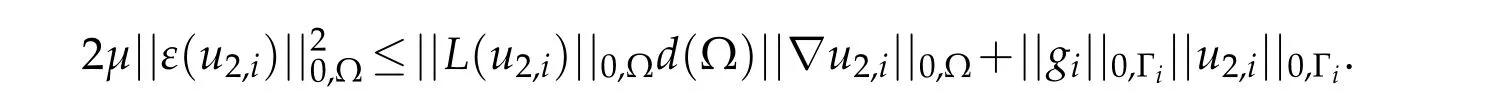
On the other hand,there exists constantsck,cpandctsuch that

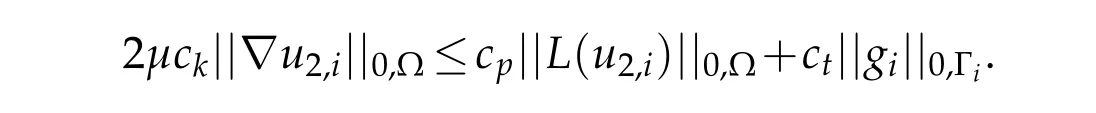
Consequently,

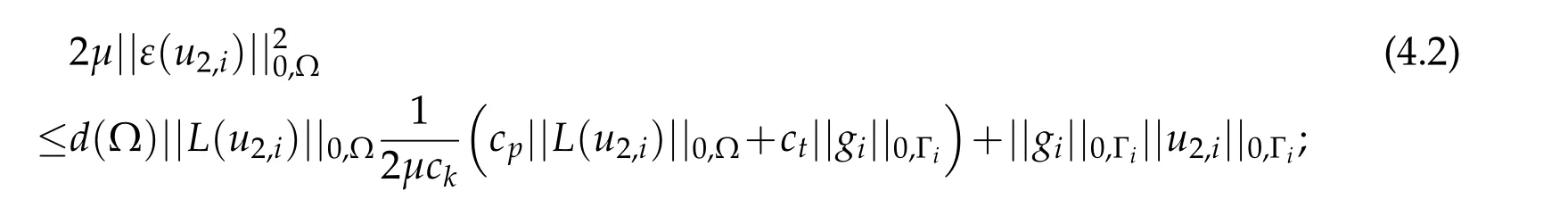
since,following(3.10)and(3.28),||gi||0,Ωare uniformly bounded with respect toϵthen,using(3.29)

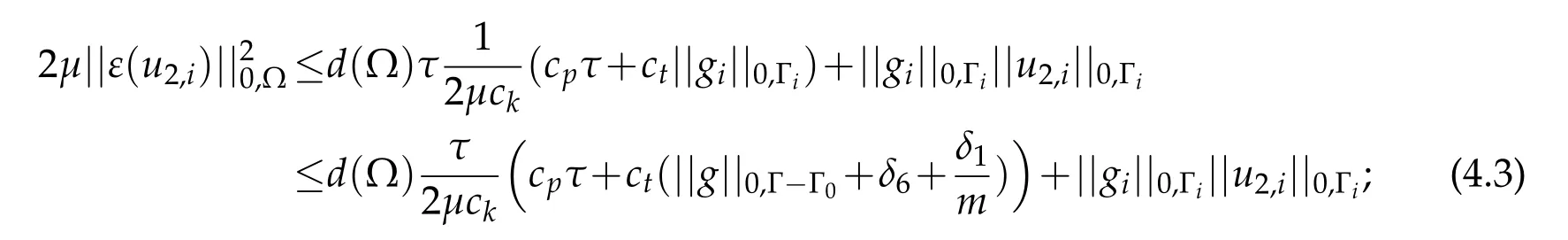
pose

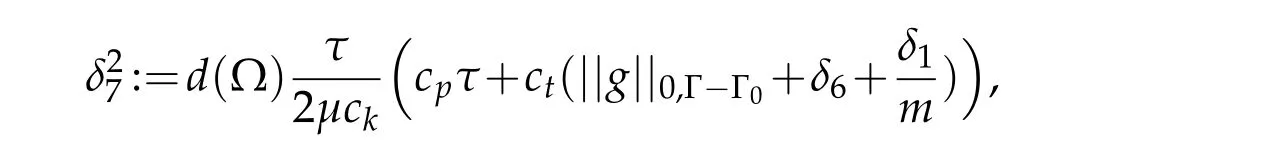
it can be made,thanks to estimate(3.29),as small as desired.Applying(3.33),(3.10)and(3.28),estimate(4.3)becomes

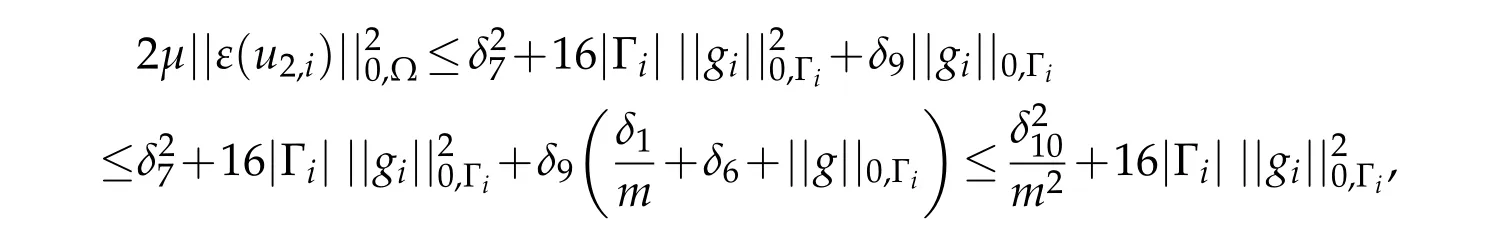
whereThen by simplifying,

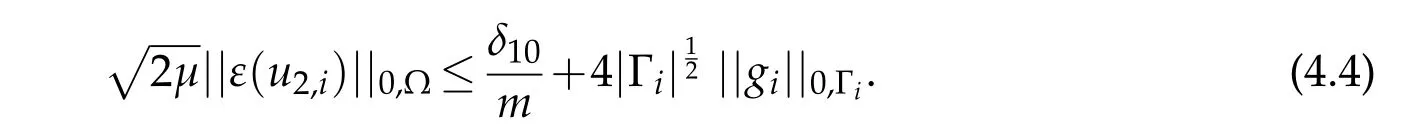
One should notice that,from the definition of the constantsδ6,δ7andδ9,the constantδ10can be made as small as desired.

Step 2:Since the deformationε(u2,i)is a linear application with respect to the first derivatives ofu2,ithen,with the same notations as in(3.30)and by using(3.31),we have

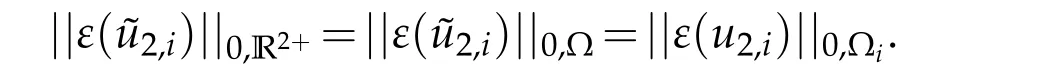
Applying the estimate stated in([11],Corollary 1.2.2)togives

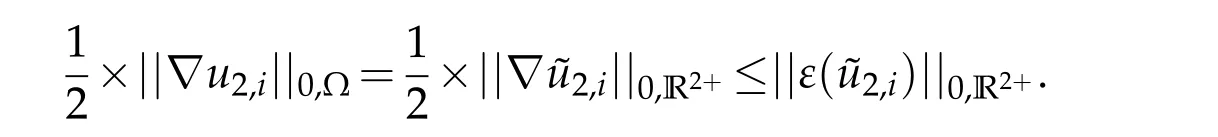
Thus,(4.4)becomes

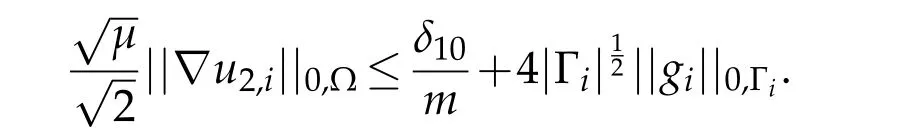
Using young inequality yields

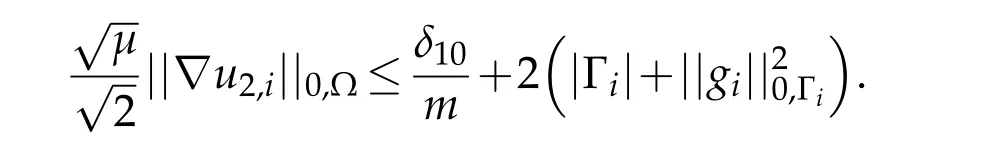
Using approximation result(3.10),we have

Summing overwe obtain using triangular inequality

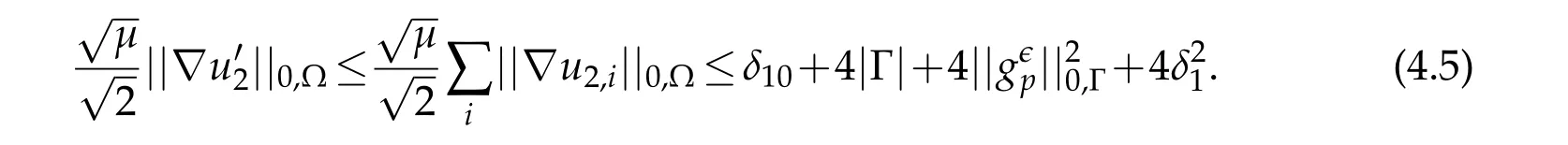
Finally,combining(4.1)and(4.5),we get

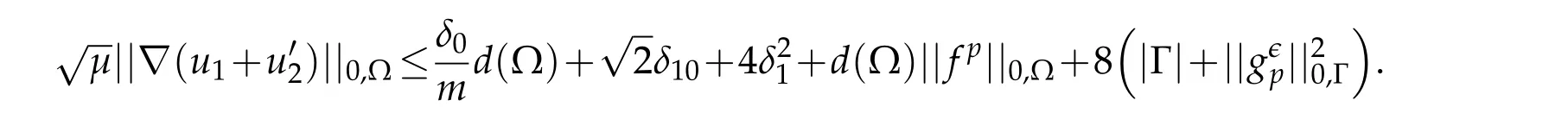
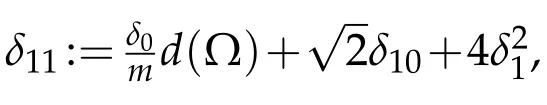
Using(3.28),estimate(4.6)becomes

and using(3.5)and(i)of(3.7),estimate(4.7)becomes

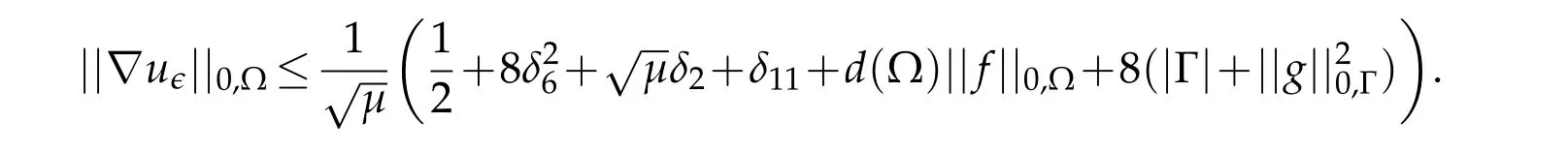
By adequately choosing the positive numberswe immediately get

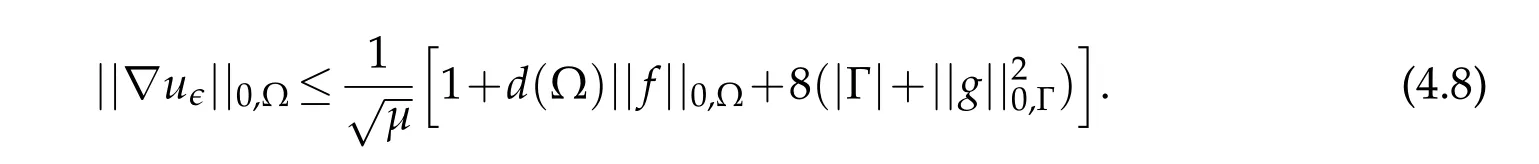
We conclude the theorem foruby applying(a)of Lemma 2.2 on one hand,and(iii)of Remark 2.2 on the other hand.

Finally;in order to get the explicitH1estimate ofuϵ,and so that ofu,we use the Poincaré inequality(3.32)to bound||u||0,Ωat one hand and the estimate(1.7)at the other hand.

5 Conclusion

In the point of view of numerical analysis,estimate of Theorem 1.1 is interesting.Indeed,error estimates in finite element method of the type

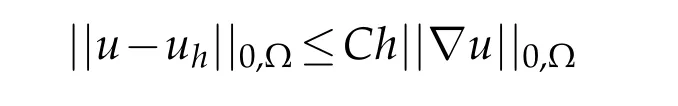
involve the quantity||∇u||0,Ω.Assuming that the constantCcan be explicitly computed,then it is possible to explicitly bound||∇u||0,Ωwhich implies a better estimate of||u||0,Ω.

Another interesting feature of the estimate(1.7)that makes it effective is that it does not depend on the characteristic parameters of the polygonal domain Ω,namely,the edges’s length,their number as well as the measures of the angles.The estimate is therefore indifferently applicable to all polygons.All this allows the possibility to generalize this result,by substantial approximation,to aC1class domain.

Acknowledgments

The authors would like to thank the referee for his relevant comments and remarks on the material presented in this paper as well as the editor for his support during the submission process.

Appendix A.Some clarifications

Regarding the application of the main result established in[7],we note the following facts.The part of Theorem 2.1 in[7]used in the proof of Lemma 3.2 is the equivalence between the following two assertions:

1)Xiis approximated by smooth functions with support away from Γ-Γi;

To effectively apply this result,we need to show that the factXi=0 on Γ-Γiimplies 2).Indeed,letx∈Γ-Γi.We assume for convenience,thatxcoincide with the origin(0,0)of R2.Since∂Ω is a polygon then,there existsc＞0 independent ofrsuch that

On the other hand,the functionXisolution of problem(P1)is continuous onOne can see this using the following argument:according to the definition ofApplying the Whitney extension theorem(see[12]),one can findthat coincide withXion Γ.Thus,solves the following problem

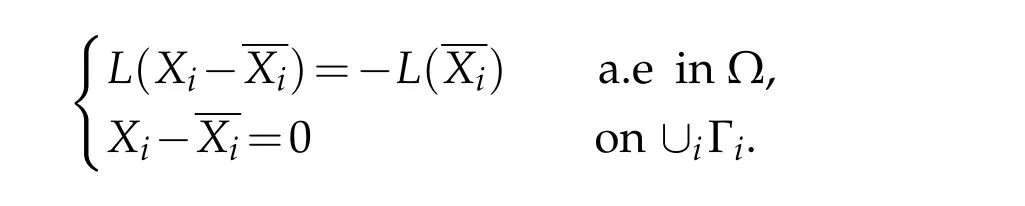
Since the boundary Γ of Ω satisfies the conditions(1.5)andthen,.Consequently

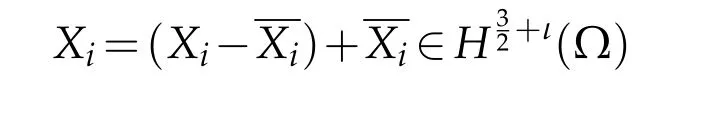
as well. Furthermore,by an adequate Sobolev embedding,and thus,the claimed continuity.The Lebesgue differentiation theorem yields:

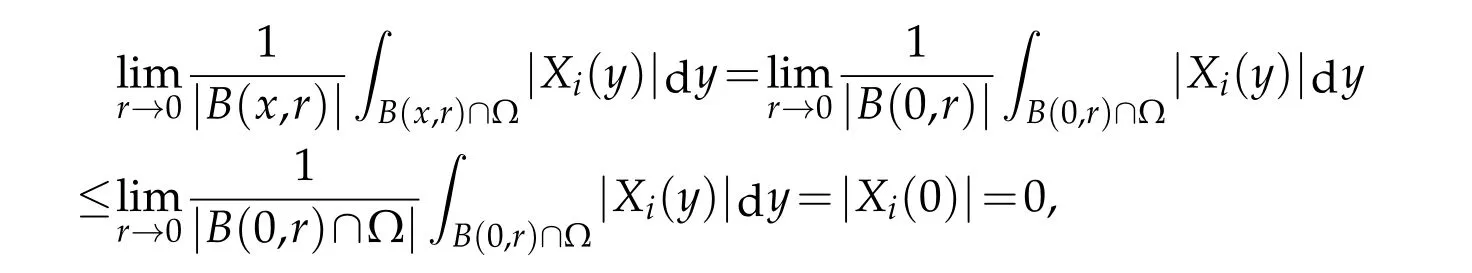
we infer that assertion 2)holds for allx∈Γ-Γiand thus,C1,2-almost everywhere.WhereC1,2refers to the 2-capacityof the set Γ-Γi.

Finally,one can show continuity of the functionYithat solves problemP4by remarking thatand by applying the same argument used for justifying the regularity of the solutionuof problem(1.1),one easily infer thatand gets the same conclusions as forXi.