Quenching Time Estimates for Semilinear Parabolic Equations Controlled by Two Absorption Sources in Control System

DAI Xiaoqiang,YANG Chao,HUANG Shaobin and WU Fei

1 Department of Electronic Information,Jiangsu University of Science and Technology,Zhenjiang 212003,China.

2 College of Computer Science and Technology,Harbin Engineering University,Harbin 150001,China.

3 No.704 Institute of China Shipbuilding Industry Corporation(CSIC),Shanghai 200000,China.

Abstract.This paper deals with the quenching solution of the initial boundary value problem for aclass of semilinear reaction-diffusion equation controlled by two absorption sources in control system and estimate upper bound and lower bound of the quenching time.We point that the number of absorption sources influences the time of quenching phenomenon.The solution can solve some boundary value problem in control system.

Key Words:Reaction-diffusion equation;Dirichlet boundary;quenching time;control system.

1 Introduction

The purpose of the present paper is to consider the quenching phenomenon for the initial boundary value problem(IBVP)of semilinear reaction-diffusion equation

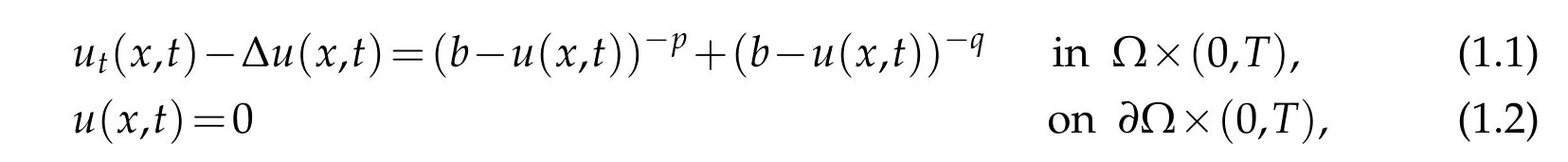
where 2＜p＜q,b=const＞0,Ω⊂RNis a bounded domain,∂Ω is its smooth boundary,andu0(x)is the nonnegative initial data inandWe define(0,T)to be the maximal existence time interval of the solutionuof(1.1)-(1.3)throughout the whole paper. The solutionu(x,t)of(1.1)-(1.3)has the following properties:u(x,t)has twice continuous derivate inx ∈Ω and once inu(x,t)＜bfor allt ∈(0,T).Problem(1.1)-(1.3)represents an elastic membrane inside an idealized electrostatically actuated MEMS.

Definition 1.1.If T=+∞,we say problem(1.1)-(1.3)admits a global solution.If T＜∞and the solution u(x,t)of problem(1.1)-(1.3)has a singularity

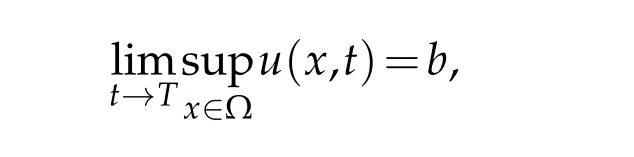
then the solution u(x,t)is the so-called quenching solution of problem(1.1)-(1.3),T is the quenching time.

In 1975,Kwawarada[1]investigated the quenching phenomena firstly,formed the basis for further investigation by various authors[2]-[11].Particularly,Boni and Bernard[7]studied a class of parabolic model with a single absorption source

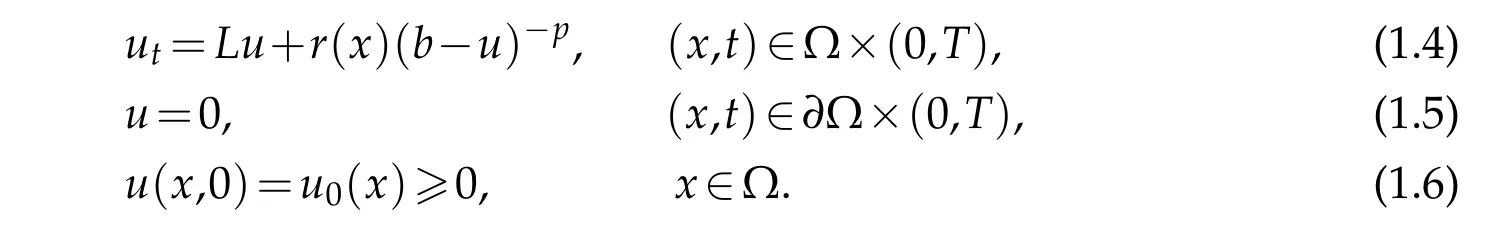
Further,they obtained the quenching phenomena of problem(1.4)-(1.6)and estimated the quenching time.Also,they clearly demonstrated that the absorption source term has an pronounce affect on the quenching phenomenon for the nonlinear reaction diffusion equation. Xu[9]investigated initial boundary value problem(1.4)-(1.6)for nonlinear parabolic differential equations with several combined nonlinearities and carries out numerical experiments.Selcuk[10]and Ozalp[11]showed quenching phenomenon occurs on the singular boundary conditions.The present paper focuses on the solution of the same type of equation with two absorption sources,which are both positive.We change the exponents of both two absorption sources such that the two terms have a large enough gaps in the sense of growth order,in order to reveal and compare the importance of the two factors acting on the behavior of the quenching phenomena,which are the number of the absorption source terms and the exponents of these terms. The results obtained in the preset paper suggests the dominant influence of the exponents of the absorption terms comparing the number of them,which is not only different from the classical heat equation with nonlinear power-type external force[12,13],but also different from the nonlinearities and their corresponding behaviours and affects in other models[14–30].

The paper consists of following sections:In Section 2,we show the local solution of problem(1.1)-(1.3)by approximation method.In Section 3,we prove the quenching phenomenon and estimate the quenching time by the maximum principle and corresponding ODE theory.

2 Local existence

Firstly,we prove that the solution locally exists.

Theorem 2.1.Problem(1.1)-(1.3)admits a unique local solution onΩ×(0,T),where T ＜∞.

Proof.LetV(x,y,t)be the fundamental solution of problem

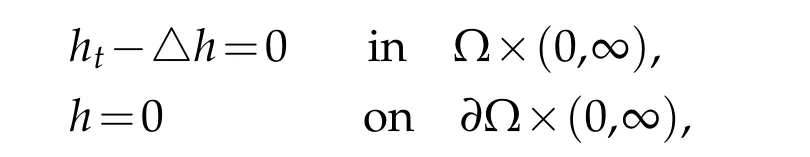
Then problem(1.1)-(1.3)has the solution of the following form

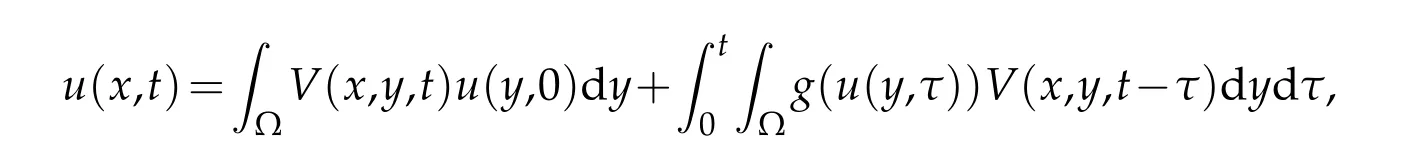
where(x,y,t)∈Ω×Ω×(0,T)andg(u)=(b-u)-p+(b-u)-q.

Next we construct the function sequence{un}by putting

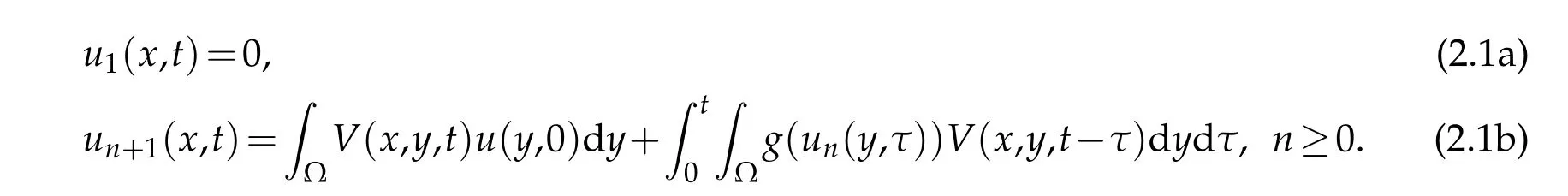
It is obvious thatun ＞0 for alln ＞1,asg(u)is increasing andV(x,y,t)＞0.From the recurrence of(2.1),we can getun+1≥unin Ω×(0,T).

Assume thatu0(x)≤b-2γandun≤b-γ,whereγis a positive number.We claim thatun+1has upper bounds,andun+1≤b-γon a small time interval.From(2.1),we have

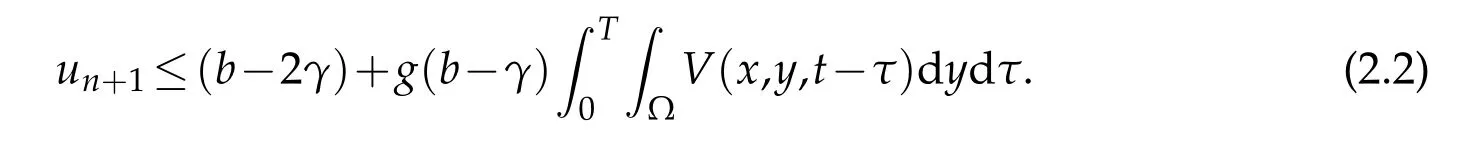
As

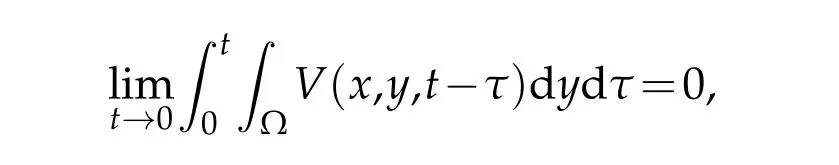
there exists a small enoughTsuch that

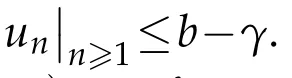
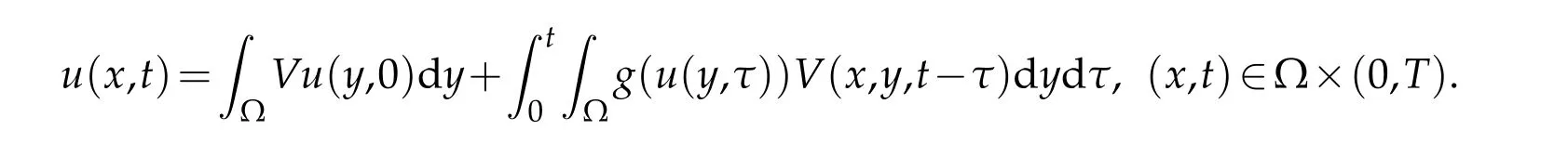
3 Quenching time

In this section,we investigate the quenching phenomenon of the problem(1.1)-(1.3)and estimate the time of quenching.

For the initial datum,we define its supremum by takingx=a∈Ω as follows

Show the eigenvalue problem as follows

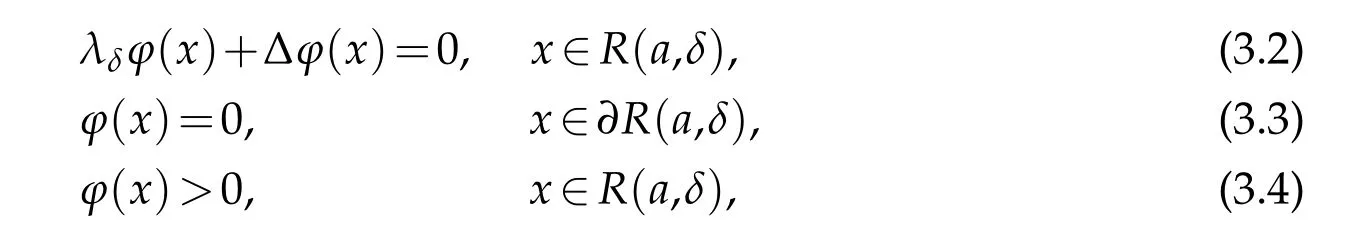
whereR(a,δ)={x∈RN:|x-a|＜δ}⊂Ω forδ＞0.Boni and Bernard[7]pointed that there exists a solution(φ,λδ)of problem(3.2)-(3.4)satisfyingwhereD＞0 depends on the dimensionNand the upper bound of the coefficients of the operator Δ.Further,we define

Next,we show the main theorem.

Further we estimate its quenching time T as follows

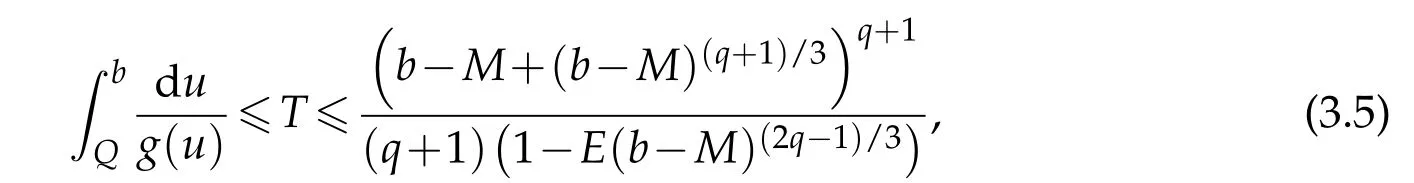
where g(u)=(1-u)-p+(1-u)-q.

Proof.Sinceby the mean value theorem,there exists ax0∈R(a,δ)satisfying

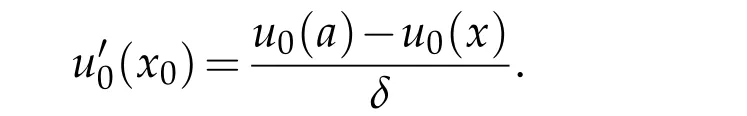
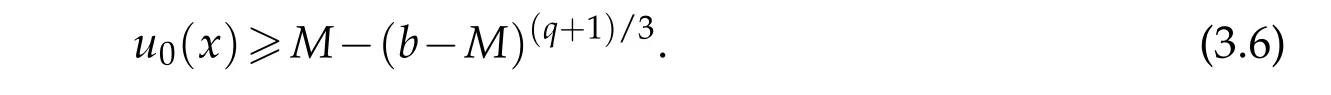
Letφ(x,t)be a solution of the following IBVP

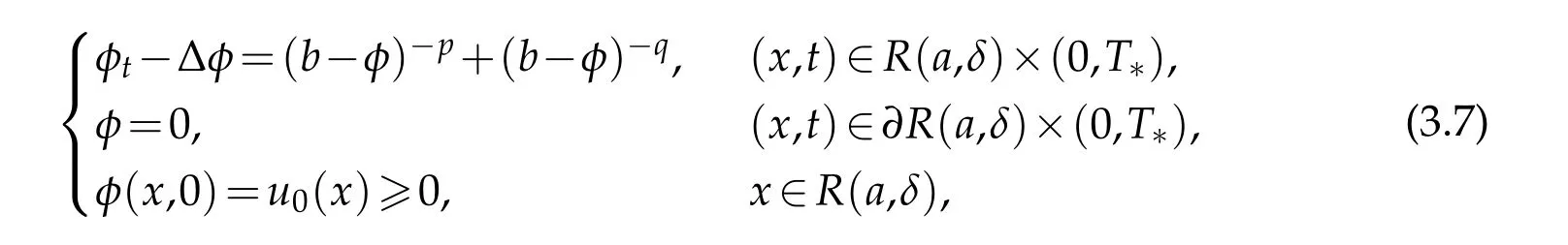
whereT*is the maximal existence time ofφ(x,t).Sinceφ(x,0)=u0(x)≥0 inR(a,δ),from the maximum principle,it follows thatφ(x,t)≥0 inR(a,δ)×(0,T*). We definel(t)as follows

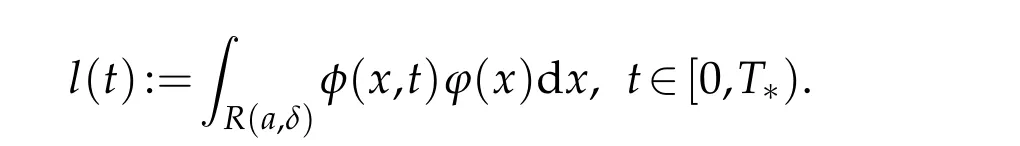
Through using(3.2)and(3.7),we have the derivative ofl(t)

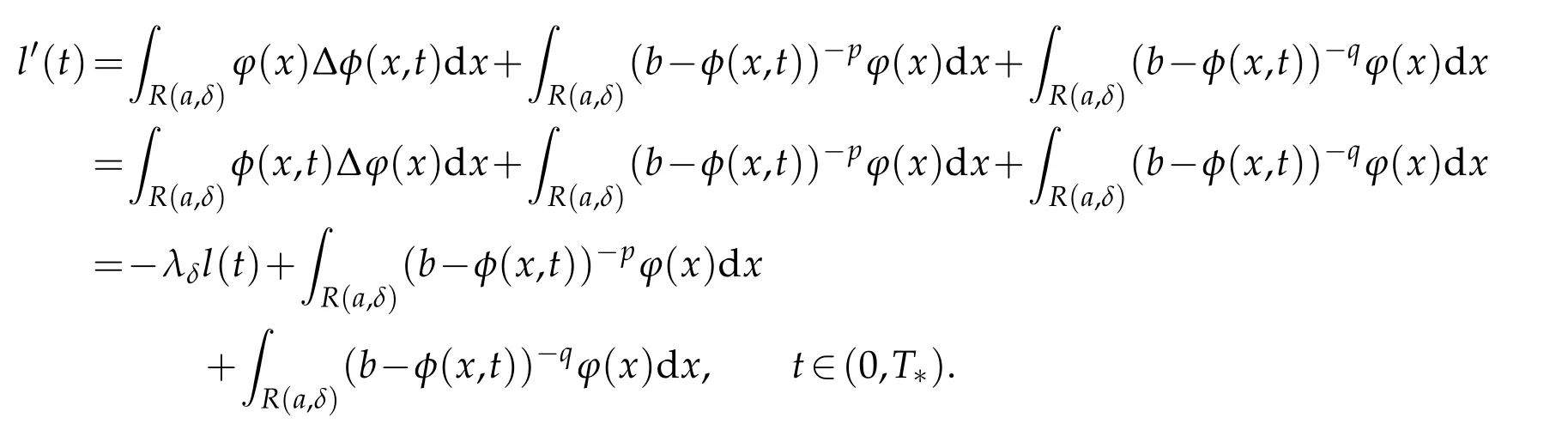
By Jensen’s inequality,we have

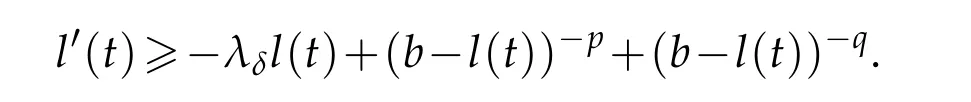
Combined withl(t)∈[0,b]for 0＜t＜T*and

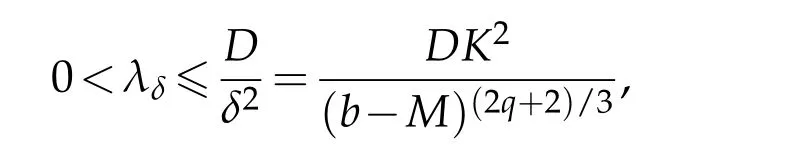
we obtain that

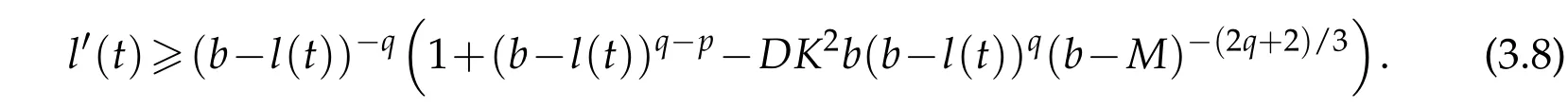
From(3.6),we have

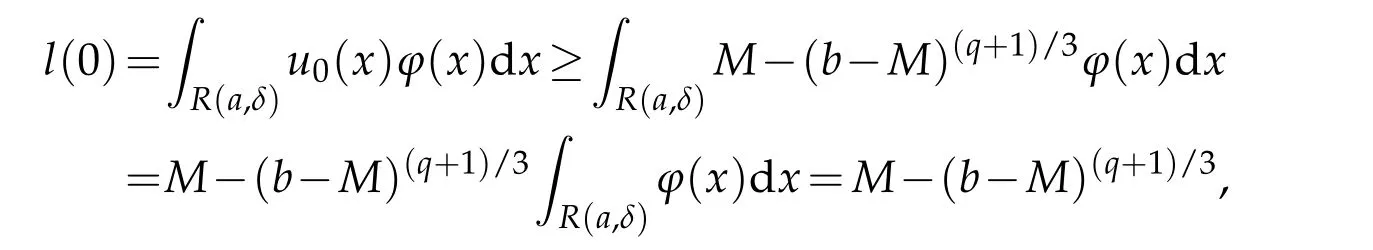
that is

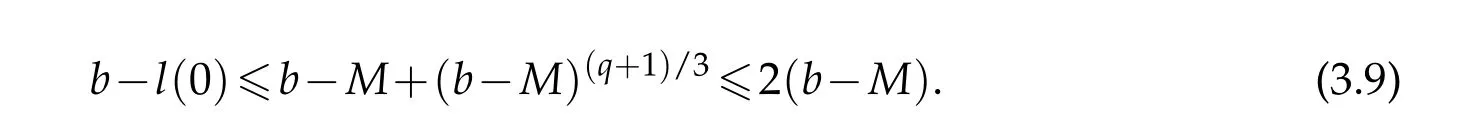
From(3.8)and(3.9),we have

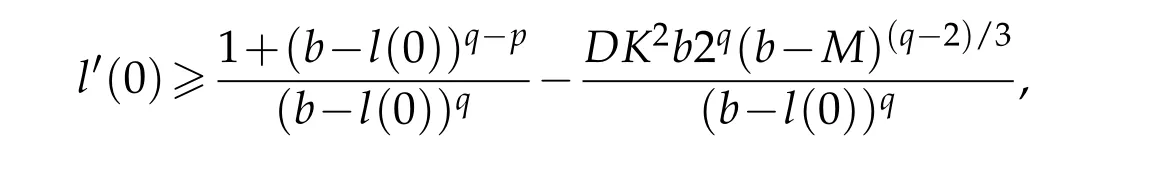
that is

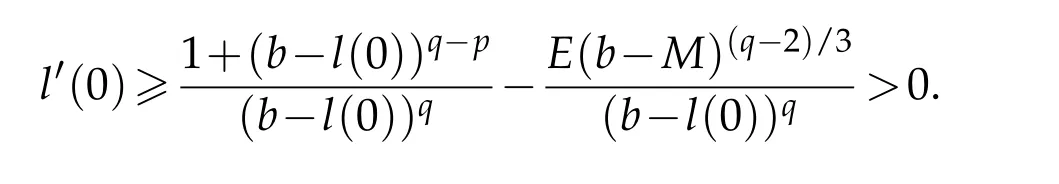
Next we prove

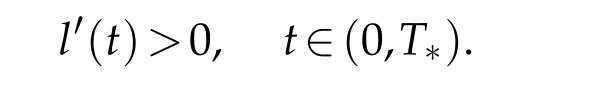
Arguing by contradiction,we suppose thatt1∈(0,T*)is the first time thatl′(t)＞0 fort∈[0,t1)andl′(t1)=0.Then we seel(t1)≥l(0),which means

which is a contradiction.Hence we have

Further we obtain

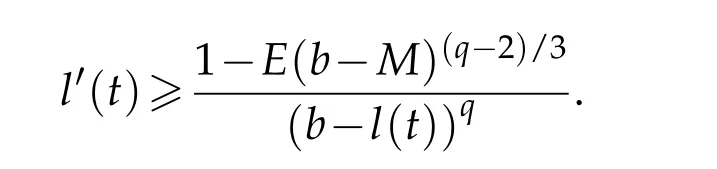
By the direct calculation,one sees

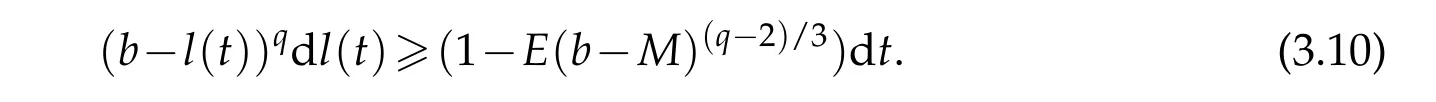
Integrating(3.10)from 0 toT*with respect totgives

that is

Since the right hand of(3.11)is bounded,we obtain thatφ(x,t)quenches in a finite time.Using the maximum principle,it impliesu(x,t)≥0 in Ω×(0,T).And extending the estimate,we get

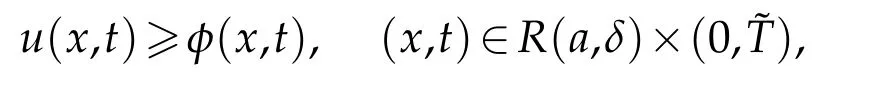
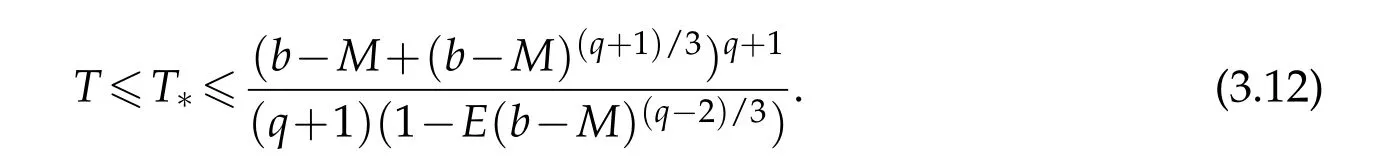
In fact,assume thatT ＞T*,we seewhich contradicts the interval(0,T)of the solutionu.From the finiteT,ut＞0,andu＜b,we see thatuquenches in a finite time.

In the subsequence,we discuss an ODE problem to show the lower bound ofT

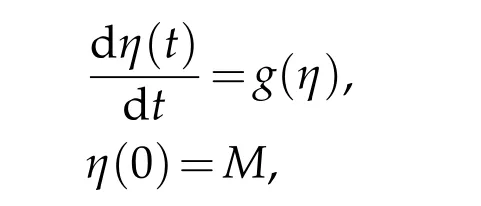
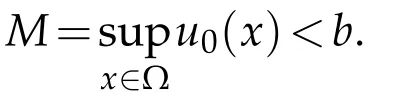
Assume thatwe have

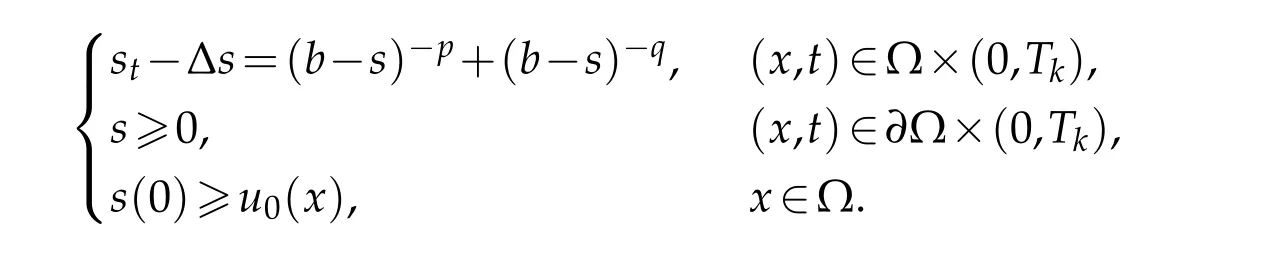
By the maximum principle,one sees 0≤u≤s=η(t),(x,t)∈Ω×(0,Tk).

Henceg(u)＞0 implies

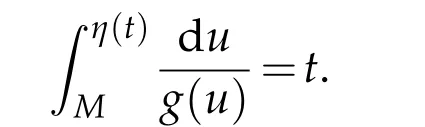
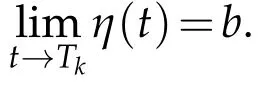
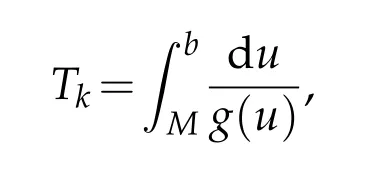
which implies that

However ifTk＞T,thenη(T)≥‖φ(x,T)‖∞=b,which contradicts the interval(0,Tk)of the solutionη(t).

Combined with(3.12)and(3.13),we have the following estimate forT

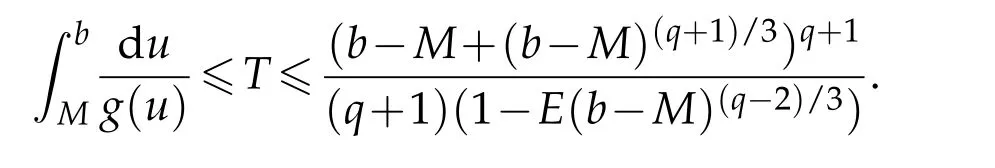
Authors’contributions

Dr.Xiaoqiang Dai suggested the research topic and finished the main part of such research. Mr. Chao Yang wrote the main codes to simulated the solution and to verify the behavior of the quenching phenomena in the numerical way. Dr. Shaobin Huang checked all the arguments.Dr.Fei Wu conducted the corresponding experiments and the verification of the model and the special nonlinearities.All of them were involved in the work of revision and approved the final manuscript.

Acknowledgement

The authors thank Prof.Yanbing Yang and Dr.Mingyou Zhang for their constructive suggestions.