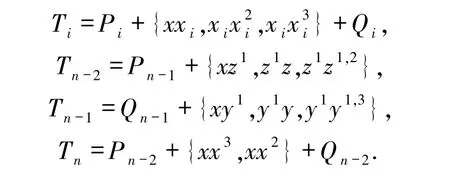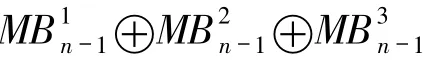由轮生成的Cayley 图的广义3 -连通度
张 燕, 马木提·阿依古丽
(新疆大学 数学与系统科学学院,新疆 乌鲁木齐830046)
1 引言及预备知识
令G =(V,E)表示点集为V(G)和边集为E(G)的图.任意一点v∈V(G),
NG(v)={u∈V(G)\{v}|uv∈E(G)}
表示v在G中的邻集. v 在G 中的度,记为dG(v),其中dG(v)=|NG(v)|. Δ(G)和δ(G)分别表示G的最大度和最小度.若Δ(G)=δ(G)=k,则称G 是k-正则的.任意点x,y∈V(G),记(x,y)-路P ={x =x0,x1,…,xk=y},其起点是x,终点是y,内部点是x1,x2,…,xk-1.若路P上的两点是连续的,则这两点是相邻的.一个长为1 的路是一个边,简记xy.若G中的2 条(x,y)-路P 和Q没有公共内部点,则称它们是内部不交的,也就是说,V(P)∩V(Q)={x,y}.若
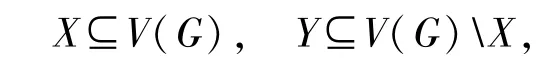
则(X,Y)-路是一族由起点为x∈X,终点为y∈Y,且内部点既不属于X,也不属于Y 的内部不交路.特别地,若X ={x},则(X,Y)-路是一族由起点为x,终点为Y中不同点的内部不交路.对于未提到的图的理论符号和术语,参考文献[1].
传统连通度κ(G)是图G的点子集X的最小基数,使得G-X 是不连通的或平凡的.若κ(G)≥k,则图G 是k -连通的.众所周知,Whitney[2]提出了与连通度等价的定义.若S ={u,v}是V(G)中的任意一个2 元-子集,则κ(G)表示G 中内部不交的(u,v)-路的最大数目.作为传统连通度的一个推广,Chartrand等[3]在1984 年提出了广义k -连通度.这个参数可以通过连接图G中的任意k个点来衡量图G的容错性.令G是一个阶为n的连通图,S是图G中任意一个k 个点的集合,其中k 是整数,且2≤k≤n,若S⊆V(T),则称树T是G的一个S-树.令{T1,T2,…,Tr}是图G的S-树的集合,若
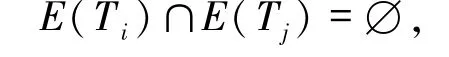
且
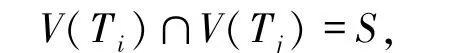
其中1≤i≠j≤r,则称其是内部不交的.令κG(S)表示图G中内部不交S-树的最大数目,用κk(G)表示图G的广义k-连通度,其中
显然G的广义2 -连通度κ2(G)恰好是κ(G).
近几年,广义k-连通度受到了一些关注,Li[4]证明了一般图G是否存在k个内部不交的S-树是NP-完全问题,其中S⊆V(G),|S |=k,且k是固定的整数.目前,已经有了关于广义连通度的上界和下界的结果[5].除此之外,还有一些关于某类图的广义k-连通度的结果,但大多是关于k =3 或4.例如,Li 等确定了卡氏积图[6]、星图[7]、冒泡排序图[7]及由树和圈生成的Cayley 图的广义3 -连通度[8].Lin等[9]确定了超立方体的广义4 -连通度等,其中由圈生成的Cayley 图—修正冒泡排序图MBn的广义3 -连通度的结果如下:
定理1.1[8]κ3(MBn)=n-1,其中n≥3.
在本文中,主要研究由轮生成的Cayley 图WGn,并证明下面的结论:
定理1.2 κ3(WGn)=2n-3,其中n≥4.
令Vn是由集合{1,2,…,n}生成的n!个不同置换的集合.令p =p1p2…pn是Vn中的一个置换,其中pi表示置换p 的第i 位.对换φi,j是一个交换已知置换的第i位和第j位的函数,其中1≤i <j≤n,且一般定义如下:已知p =p1p2…pn是Vn中的一个置换,则
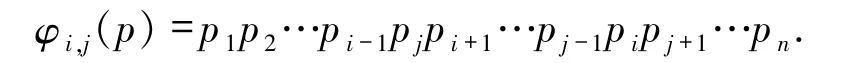
Shi[10]提出了有关Cayley图Cay(Sym(n),T)的概念,其中Sym(n)是在{1,2,…,n}上的对称群,T是Sym(n)的对换集合. G(T)表示点集是{1,2,…,n},边集是{ij |(ij)∈T}的图,称G(T)为Cay(Sym(n),T)的生成图.
若G(T)是一个单圈图,UGn表示单圈-对换图Cay(Sym(n),T).特别地,若G(T)是一个圈,则称UGn是修正冒泡排序图MBn.图1 和图2 分别表示MB3和MB4.众所周知,UGn是一个n -正则n-连通二部点传递图.
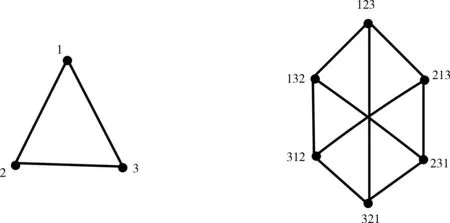
图1 由三角形生成的修正冒泡排序图MB3Fig. 1 The modified bubble sort graph MB3 generated by a triangle
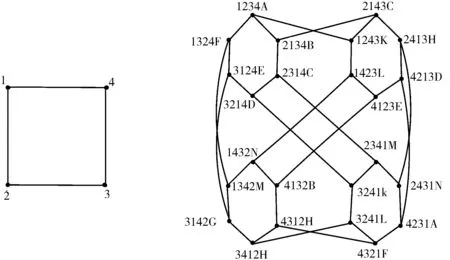
图2 由C4生成的修正冒泡排序图MB4Fig. 2 The modified bubble sort graph MB4 generated by C4
若G(T)是一个轮图Wn,WGn表示轮-对换图Cay(Sym(n),T),其中轮图是由一个单点与一个(n-1)-圈上所有点相连形成的图. W4和WG4如图3 所示.从定义可知,WGn是一个(2n -2)-正则二部点传递图[11].
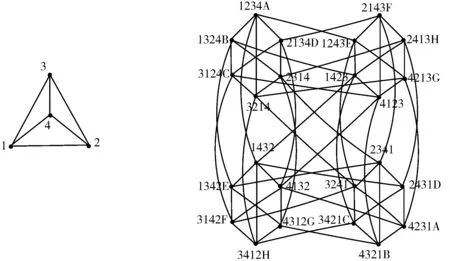
图3 由轮图W4生成的Cayley图WG4Fig. 3 The Cayley graph WG4 generated by wheel graph W4
下面的引理将会用于定理1.2 的证明.
引理1.1[5]若存在2 个度为δ(G)的相邻点,则κk(G)≤δ(G)-1,其中3≤k≤|V(G)|.
引理1.2[1]若G是一个k-连通图,x是G中的任一点,Y⊆V\{x}是至少有k个点的集合,则在G中存在k条内部不交且终点是Y中不同点的(x,Y)-路.
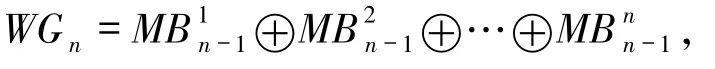
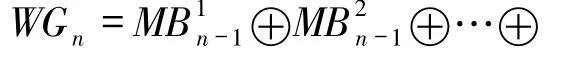
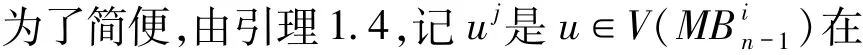
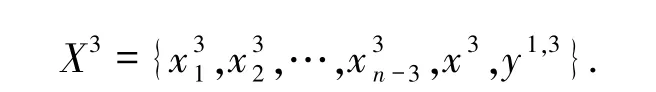
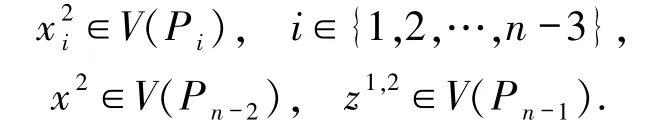
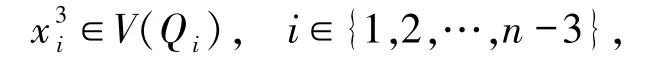
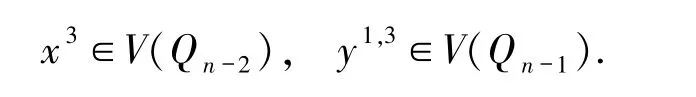
对每个i∈{1,2,…,n-3},令