Ree 群2G2（q）自同构群阶分量刻画的简化证明

贾松芳， 陈彦恒， 姜友谊

（重庆三峡学院 数学与统计学院，重庆 万州404100）

本文涉及的群皆为有限群，单群指的是非交换单群.

设G是一个群，π（G）表示｜G ｜的全部素因子的集合.文献［1］定义了群G的素图Γ（G），它是满足下列条件的简单图：

1）V（Γ（G））＝π（G）；

2）2 个顶点p、q在Γ（G）中有边相连的充要条件是群G中含有pq阶元.

记Γ（G）的连通分支的个数为t（G），Γ（G）的第i 个连通分支的顶点集为πi（G），i ＝1，2，…，t（G）.规定如果2 ｜｜G ｜，2∈π1（G）.于是｜G ｜可写为

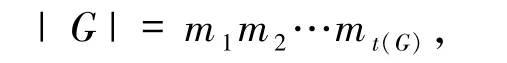
其中π（mi）＝πi（G），i ＝1，2，…，t（G）.文献［2］中把m1，m2，…，mt（G）称为群G 的阶分量，且把群G的阶分量的集合记为OC（G），即

文献［2］在研究Thompson 猜想［3］的过程中提出群的阶分量这一概念，并提出了单群的阶分量刻画问题，即通过单群的阶分量集合确定该单群.文献［4］证明了：若单群M 能被其阶分量刻画，则Thompson猜想对M 也成立.因此单群的阶分量刻画问题是Thompson猜想的推广.

阶分量对素图连通的单群的结构影响有限，但对素图不连通的单群的结构有着重要影响，散在单群、Suzuki-Ree群等众多系列单群都可以被它们自身的阶分量刻画（参见文献［2，5 -20］）.文献［21］证明了Suzuki-Ree 群的自同构群Aut（2F4（q）），q ＝2f和Aut（2G2（q）），q ＝3f，其中f ＝3s，s 为正整数，可由其阶分量刻画，这是阶分量刻画问题在几乎单群中成功的尝试.但并非所有的几乎单群都能被其阶分量刻画，比如O7（3）、S6（2），它们有相同的阶分量集合（见文献［22］），到底还有哪些几乎单群可以被其阶分量刻画，还是一个有待继续研究的课题.但本文需要指出的是：上述阶分量刻画的文献的证明过程无一例外的都根据单群分类定理，结合给定几乎单群的阶分量，对全部单群一类一类的核查排除，直至剩下目标单群.这个过程无疑是繁琐的和机械的.如果能够根据目标单群的自身特征先对单群分类，缩小核查范围，那么肯定会给证明过程带来简化.

本文借助Sylow 2 -子群阶数≤8 的单群的分类，证明了Ree群2G2（q）（q ＝33s，s≥1）的自同构群可由阶分量刻画，与文献［21］的命题3 相比较，证明过程被简化.

文中其他未做说明的符号和术语都是标准的，可参见文献［23 -24］.

1 预备知识

为了方便，下面列出4 个结论作为预备引理.

引理1.1［25］设G 是一个偶数阶的Frobenius群或2 -Frobenius群，则t（G）＝2.