电磁式磁性珩磨系统温度场及风冷效能研究*

李 昂，姚新改,2*，王 硕，董志国,2

（1.太原理工大学 机械与运载工程学院，山西 太原 030024；2.精密加工山西省重点实验室，山西 太原 030024）

0 引 言

不锈钢管因具有耐腐蚀性、高强度等优点，在工业中得到了广泛应用。但在不锈钢管生产过程中，其内表面极易形成一层氧化皮，使得其在一些领域上的应用遭到限制[1]。

磁性珩磨技术将磁力技术与珩磨技术相结合，通过磁场之间的相互作用力，驱动磁性珩磨头紧贴钢管内表面，与不锈钢管做相对运动从而去除氧化皮[2]。在磁性珩磨加工过程中，由于电磁能与机械能之间相互转化，系统内部产生各种损耗，加之散热条件不佳，会导致磁性珩磨系统工作时发热严重，不能持续加工；同时，温度过高也会加快铜线绕组的老化。因此，准确计算出磁性珩磨系统的温度场非常重要[3]。

电磁式磁性珩磨系统工作原理与永磁电机相似，目前，国内外学者针对电机温度场已经做了大量研究。张璐璐等[4]采用电磁—热双向耦合的方法，对轮毂电机的温度场进行了分析，并研究了气隙长度等结构参数对温升的影响；王天煜等[5]对兆瓦级高速永磁电机进行了流—热—固耦合计算，得到了电机转子温度场及其传热规律；冯海军等[6]建立了全封闭扇冷电机三维温度场模型，采用等效导热系数的方法解决了流动空气的问题，并对电机各部位的温升进行了分析；冯桂宏等[7]采用场路耦合协同仿真的方法，计算了挤塑机直驱永磁电机的温度场，并进行了温升实验，验证了仿真结果；杨慧等[8]通过研究，实现了电磁场和温度场的单向耦合，得到了磁性珩磨系统温度场，为磁性珩磨的设计提供了理论依据；王雷超等[9]建立了磁性珩磨性系统水冷模型，通过Fluent仿真，模拟计算得到了有水冷时的温度场，并进行了试验，验证了水冷系统的可靠性。

本文对电磁式磁性珩磨系统展开研究，首先建立磁性珩磨系统三维稳态温度场模型，采用有限元法对磁性珩磨系统运行时的温度场进行仿真计算，得到自然冷却时系统温升变化曲线；为解决现有水冷系统存在的系统复杂以及漏水等问题，设计风冷系统，通过Fluent仿真计算得到风口风速，重新计算散热系数得到有风冷时系统最高温度；设计并进行磁性珩磨系统温升实验，验证仿真计算结果的正确性。

1 磁性珩磨加工原理

磁性珩磨系统由旋转磁场发生器和磁性珩磨头两部分组成，其原理图如图1所示。

图1 磁性珩磨系统原理图1—定子铁芯；2—绕组；3—钢管；4—珩磨条；5—永磁体；6—45钢；7—支撑轴；8—外壳

工作时，旋转磁场发生器通入三相交流电，产生旋转磁场，使得磁性珩磨头在一定的压力下在不锈钢管内腔作圆周运动，珩磨头对钢管内表面进行挤压切削，最终达到去除氧化皮的目的[10]。

2 磁性珩磨系统损耗分析

磁性珩磨系统的损耗主要有铜损、铁损以及摩擦损耗。

2.1 铜耗计算

磁性珩磨系统中的铜耗来源于电流通过绕组产生的损耗，其计算公式如下：

Pcu=mI2R

（1）

式中：m—电机相数；I—通过绕组的电流有效值，A；R—绕组电阻值，Ω。

在设计工况下，当磁性珩磨系统运行至稳态温升阶段时，测量绕组相电流；断电后迅速测量绕组电阻，得到电流为2.51 A，电阻为4.8 Ω；根据式（1）计算得到绕组铜耗损为90.7 W。

2.2 铁耗计算

磁性珩磨系统的定子铁芯处产生的铁耗由3部分组成，分别是磁滞损耗（Ph）、经典涡流损耗（Pc）以及附加涡流损耗（Pe）[11]。其计算公式为：

（2）

式中：PFe—铁耗，W；α—磁滞损耗次幂；kh—磁滞损耗系数；kc—涡流损耗系数；ke—涡流损耗系数；f—磁场频率，Hz；Bm—磁密幅值，T。

定子铁芯的材料为DW465-50硅钢片。查阅不同频率下的损耗曲线，通过曲线拟合工具得到各项损耗系数分别为：α=1.74，kh=23.18，kc=18.73，ke=3.25。

在CEDRAT Flux中，笔者对额定负载下磁性珩磨系统进行稳态计算，得到磁性珩磨系统定子铁芯损耗为44.3 W。

2.3 摩擦损耗计算

磁性珩磨属于精加工，材料去除力很小可以忽略不计，只须计算摩擦损耗即可。摩擦损耗为珩磨头对不锈钢管进行磨削时产生，其计算公式为：

（3）

式中：Tl—磨具的阻力矩，其计算公式为：

Tl=k×μ×Force_y×d

（4）

式中：r—工件内壁半径，m；n—磨具转速，r/min；d—工件内壁直径，m；k—安全系数；μ—摩擦系数；Force_y—永磁铁径向方向所受吸引力，N。

工件内壁直径d=0.068 m，n=600 r/min，k取2，μ取0.5。在Maxwell中进行仿真计算，可得到Force_y=47 N。根据式（4）计算可得到Tl=3.196 N·m。

根据式（3）可以得到：当转速确定时，摩擦损耗也随之确定，与其他加工参数如进给速度以及加工行程无关；通过计算可得到Pf=200.7 W。

基于上述分析，可通过计算得到磁性珩磨系统损耗。

根据公式Q=P/V计算出的各部位的生热率，结果如表1所示。

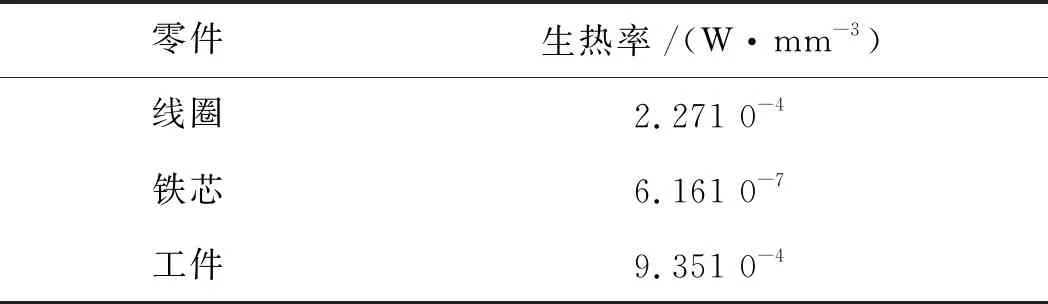
表1 磁性珩磨系统损耗

3 温度场模型的建立

3.1 求解模型

（1）各个定子槽内的导线均匀排列，槽内浸渍漆、绝缘等效为一个绝缘实体；

（2）定子铁芯之间无间隙，作为一个整体。

根据磁性珩磨系统基本参数和上述假设，笔者建立了磁性珩磨系统的求解模型，如图2所示。

本文所仿真分析的磁性珩磨系统主要参数如表2所示。

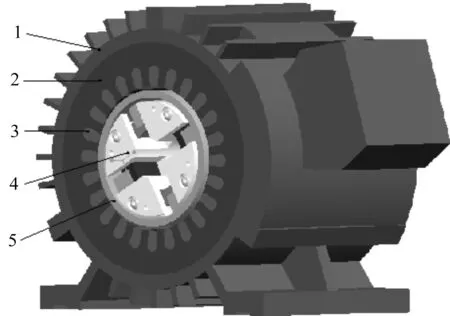
图2 磁性珩磨系统求解模型1-机壳；2-铁芯；3-绕组；4-珩磨头；5-钢管

表2 磁性珩磨系统主要参数

3.2 数学模型

根据传热学知识对磁性珩磨系统稳态温度场进行分析时，忽略方程的时间项。在直角坐标系下，温度场计算的数学方程为[12]：

（5）

式中：λx，λy，λz—材料在x、y、z方向的导热系数，W/（m·K）；T—固体温度，K；q—热源密度，W/m3；α—表面散热系数，W/（m2·K）；n—表面单位法向矢量；Tf—环境温度，K。

3.3 对流散热系数的确定

加入风冷系统后，旋转磁场发生器散热槽内具有很大的风速，与机壳间的换热方式为强制对流换热；由于定子较短，认为轴向风速相同。旋转磁场发生器前端面以及外壳的散热系数一般根据下式进行计算[13]：

α=9.73+14v0.62

（6）

式中：v—表面风速，m/s。

培养能力是物理教学的落脚点。能力是在获得和运用知识的过程中逐步培养起来的。在衔接教学中，首先要加强基本概念和基本规律的教学。要重视概念和规律的建立过程，使学生知道它们的由来；对每一个概念要弄清它的内涵和外延，来龙去脉。讲授物理规律要使学生掌握物理规律的表达形式，明确公式中各物理量的意义和单位，规律的适用条件及注意事项。了解概念、规律之间的区别与联系，如：运动学中速度的变化量和变化率，力与速度、加速度的关系等，通过联系、对比，真正理解其中的道理。

旋转磁场发生器后端面无气体吹过，可认为是自然冷却散热，查阅相关手册取15.2 W/（m2·K）。

此外，不锈钢管内表面散热系数一般根据下式进行计算：

（7）

式中：n—磁性珩磨头旋转速度，r/min；d—钢管内径，m。

4 风冷模型建立

为解决磁性珩磨系统发热快、无法持续加工的问题，笔者在原有的磁性珩磨系统基础上，设计了磁性珩磨系统风冷模型。

为了计算方便，对风管模型作了如下假设：

（1）风管内空气为低速流动，视为不可压缩流体，满足理想气体状态方程；

（2）忽略风管内壁对气流摩擦产生的损失；

（3）风管内空气流量流速等不随时间发生变化；

（4）空气垂直与进风口吹入风管内，空气在入口处分布均匀。

基于上述假设以及磁性珩磨系统基本参数，笔者建立了磁性珩磨系统风冷模型，如图3所示。

图3 磁性珩磨系统风冷模型1-风管；2-导流板；3-内出风口；4-外出风口；5-进风口

其中，风源由一台风量为110 m3/h，风压为14 kPa的旋涡气泵提供，通过管道连接从进风口将空气吹入，经过导流板分流由吹风口吹出，从而实现对磁性珩磨系统的风冷却。

笔者采用Standardk-ε模型以及壁面函数法，对风道内流体进行计算；将动量守恒方程、质量守恒方程以及湍流方程写成一个方程[14-15]，即：

div（ρUΦ）=div（ГgradΦ）+S

（8）

式中：ρ—流体密度，kg/m3；U—流体速度矢量；Φ—通用变量；Γ—广义扩散系数；div（ρUΦ）—对流项；div（ΓgradΦ）—扩散项；S—广义源项。

5 仿真与结果分析

5.1 无风冷时温度场分析

在自然冷却情况下，笔者在ANSYS Workbench中对磁性珩磨系统温度场进行仿真，讨论系统的换热条件主要是考虑各部件之间的热传导以及表面的对流换热。

忽略温度对各料导热系数的影响，磁性珩磨系统各部件导热系数、密度以及比热容如表3所示。

表3 材料属性

笔者施加热源以及边界条件后，得到了无风冷时磁性珩磨系统温度随时间变化曲线，如图4所示。

图4 无风冷时温度随时间变化曲线1-最高温度；2-最低温度

计算结果表明：无冷却时，磁性珩磨系统在加工0.7 h时温度即可达到75 ℃；达到稳态时最高温度为95.2 ℃，已经超出安全温度75 ℃。因此，为保证设备安全，应在加工一段时间后立即停止。

5.2 有风冷时温度场分析

为计算各部位的对流散热系数，笔者在Fluent中对送风管内流场进行计算；入口边界采用速度入口，出口边界采用压力出口，风管内壁界面为固体壁面类型。计算得到内出风口平均风速为8 m/s，外出风口平均风速为7.2 m/s。

由3.3节公式计算得到对流散热系数，作为边界条件在ANSYS Workbench进行仿真计算，可得到有风冷时磁性珩磨系统温度随时间变化曲线，如图5所示。

图5 有风冷时温度随时间变化曲线

计算结果表明：加入风冷系统后，磁性珩磨系统在2.5 h后达到稳态，相对无风冷时所需时间更短；绕组处温度最高，最高温度为58.5 ℃，低于安全温度75 ℃。因此，磁性珩磨系统可以持续加工。

6 电磁式磁性珩磨温升实验

6.1 实验内容

在相同的实验条件下，对比有无风冷时对系统温升的影响。实验中均采用二代珩磨头，测量绕组处温升变化。

实验目的：分析风冷装置对磁性珩磨系统温升的影响。

实验方法：采用泰仕热电偶温度仪测量系统最高温度，即绕组处温度。

实验装置：磁性珩磨系统实验平台如图6所示。

图6 磁性珩磨系统实验平台1-珩磨油箱；2-风管；3-旋转磁场发生器；4-不锈钢管；5-行程开关；6-旋涡气泵；7-变频器；8-输风管

6.2 实验结果及分析

无风冷系统时，在加工0.8 h后绕组处温度达到75 ℃需立即停止实验。

在相同实验条件下，有风冷时磁性珩磨系统绕组处温升曲线如图7所示。

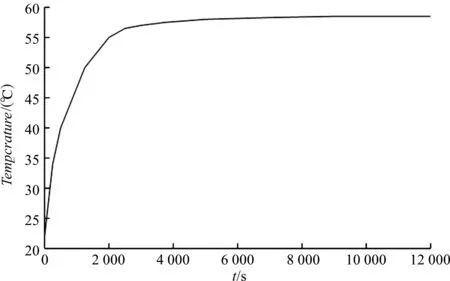
图7 有风冷时绕组处温升曲线

由图7的结果表明：系统在2.7 h后达到热平衡，最高温度为59.3 ℃，低于安全温度；实验结果均在工程允许误差范围内。

由此可见，加入风冷系统可以有效解决磁性珩磨系统不能持续加工的问题。

7 结束语

本文建立了电磁式磁性珩磨系统温度场模型，通过对系统内部产生的各种损耗进行了分析计算，得到了额定工况下的磁性珩磨系统温升变化曲线；为解决系统温升过高的问题，笔者设计了风冷系统，计算得到了有风冷时磁性珩磨系统温升变化曲线，结果表明：有风冷时磁性珩磨系统可以稳定加工；笔者进行了磁性珩磨系统温升实验，分别对有无风冷时磁性珩磨系统绕组处温度进行了测量，结果与仿真结果相比误差较小，由此验证了仿真结果的正确性。

研究结果表明：加入风冷系统，可以有效实现电磁式磁性珩磨系统的持续加工。