金沙江白格滑坡运动过程分析及潜在不稳定岩体预测
赵 程,范宣梅,杨 帆,周 礼,郭 晨
(成都理工大学地质灾害防治与地质环境保护国家重点实验室,成都 610059)
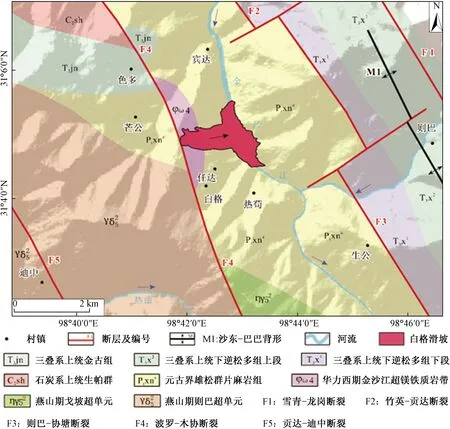
图1 白格滑坡区域地质构造图
白格滑坡发生于西藏江达县波罗乡白格村与四川省白玉县绒盖乡则巴村交界处,金沙江右岸,分别在2018年10月11日和11月3日发生两次滑坡事件,堵塞金沙江,形成堰塞湖,在人工干预下于11月13日泄流完成,险情解除[1-2]。白格滑坡并非个例。近年来,中国西南地区地质灾害频发,其中具有破坏性大、高速和携带物质多特点的滑坡碎屑流发生多次[3-4]。2009年6月5日,重庆市武隆县铁矿乡鸡尾山山体发生大规模碎屑流,造成10人死亡,64人失踪,8人受伤[5]。2017年6月24日,四川省茂县叠溪镇新磨村后山山体发生碎屑流,掩埋了坡脚整个新磨村,致使10人死亡,73人失踪[6-7]。郭晨等[8]通过无人机航测以及现场和室内试验,研究蒋刘4#滑坡呈近流体状高速远程运动堆积特征。曾琇舒等[9]在野外调查和无人机航摄数据基础上分析雷波县白沙村滑坡-碎屑流的运动过程。目前常用于滑坡碎屑流的数值模拟软件有DAN-W、DAN3D、Massflow、MassMov2D等。张睿晓等[10]以滑坡碎屑流为研究对象,通过模型试验和数值模拟结果分析拦挡结构效果。齐超等[11]通过滑坡动力分析软件DAN-W建立了Voellmy模型、摩擦模型和F-V等3种模型对东河口滑坡-碎屑流进行了模拟,得到了较好的模拟结果。高杨等[12]采用DAN3D数值方法对深圳人工堆填体滑坡运动过程进行了模拟研究,堆积范围、堆积厚度和运动速度与滑坡实际值基本吻合。夏式伟等[13]通过DAN3D软件,运用Friction-Voellmy模型模拟了汤家沟滑坡-碎屑流,分析了汤家沟滑坡碎屑流运动过程。Salvatici等[14]通过DAN3D软件,采用Voellmy模型得到碎屑流的流速和深度和实际情况有较好拟合度。Ouyang等[15]通过Massflow软件对金沙江白格滑坡进行了数值模拟,其运动过程和堆积形态与实际情况基本吻合。MassMov2D的模型是基于流体动力学方程的深度平均形式的二维有限差分解,流体被视为单相材料,其运动受流变学控制(即通过应力与应变之间的函数关系),可以通过数字高程模型(DEM)建立复杂的地形条件用以实际事件的模拟[16]。通过数字代码MassMov2D的开发和实现,可以在PCRaster GIS环境下模拟复杂地形条件下的泥石流事件[17-18]。Scaringi通过MassMov2D模型,对新磨村滑坡-碎屑流进行了反演分析,重建了滑坡的运动特征和堆积形态,对灾害风险评估有参考价值[19]。
通过使用MassMov2D模型对金沙江白格两次滑坡事件进行分析,对滑坡运动过程进行了研究,基于对已发生的2次白格滑坡的模拟,采用参数反演,并对未来最不利情况,即滑坡物源区三处潜在不稳定岩体同时失稳进行了模拟预测,获得了运动过程与堆积范围参数,结果表明三处潜在不稳定岩体同时失稳,会再次堵塞金沙江,形成堰塞湖,以期为滑坡的风险评价与防灾减灾措施制定提供理论指导。
1 滑坡区地质环境条件
白格滑坡发生于金沙江右岸的山脊处,高程3 720~2 880 m,相对高差达840 m,河谷呈“V”形发育,该区域地貌类型为构造侵蚀高山强烈寒冻风化地貌,气候类型为大陆性季风高原型气候,年平均气温7.7 ℃,平均降水量600 mm。
白格滑坡所处区域为金沙江构造带(图1),整个构造带呈NNW向展布。区域内主要分布有雪青-龙岗断裂(F1)、竹英-贡达断裂(F2)、则巴-协塘断裂(F3)、波罗-木协断裂(F4)、贡达-迪中断裂(F5)等断裂和沙东-巴巴背形(M1),其走向均为NW。其中波罗-木协断裂(F4)的总体走向为330°左右,断裂面向西倾斜,倾角50°~70°,从滑坡物源区顶部经过,对滑坡的影响较大[1]。
2 白格滑坡基本特征
2.1 滑坡基本特征
白格滑坡两次滑坡事件发生后,地质灾害防治与地质环境保护国家重点实验室在第一时间用无人机航拍获得2018年10月12日和11月5日两期影像数据,以及由四川省绘地理信息局提供的滑前1∶10 000数字高程模型(DEM)数据。通过以上数据处理后获得了滑坡区数字地表模型(DSM)、数字正射影像图(DOM)。通过ARCGIS从影像分析结合现场实地调查,将滑坡区域总体上分为三个区域:滑源区(Ⅰ)、流通区(Ⅱ)及堆积区(Ⅲ);滑坡区域后缘及两侧岩土体在滑坡发生的影响下,具有明显裂缝的三处潜在不稳定岩体K1、K2、K3(图2)[1]。
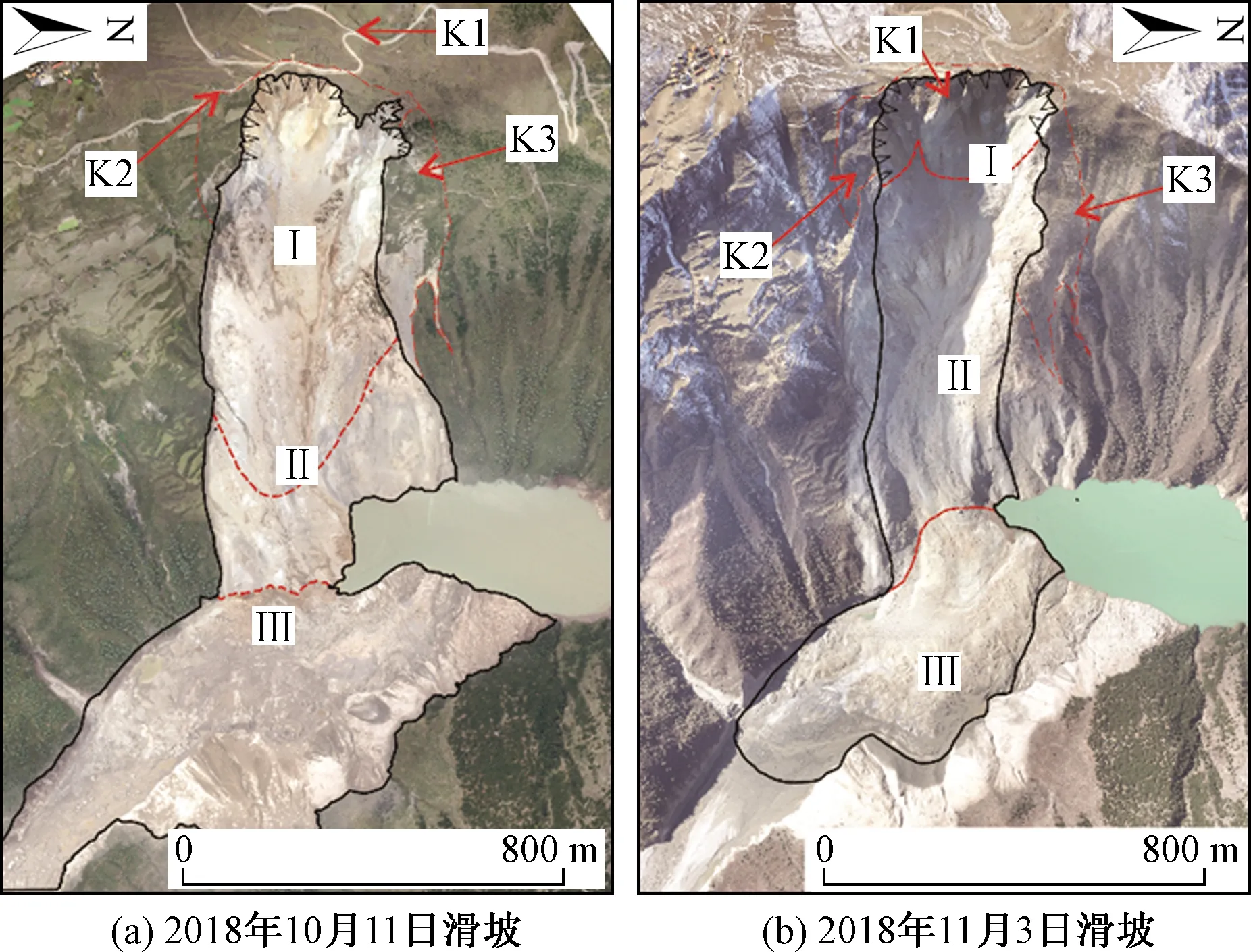
图2 白格滑坡分区图
2.2 滑坡运动特征
金沙江白格于2018年10月11日发生第一次滑坡事件,通过滑坡前后DEM差值计算其总方量约为1 960×104m3,第一次滑坡发生时,在滑源区约1 960×104m3的岩土体失稳并向下运动,其运动过程中对坡面的铲刮作用携带坡面岩土体下滑,形成碎屑流,到达金沙江后激起涌浪冲刷对岸坡面,在涌浪作用下对岸坡体部分物质被冲到堆积区,造成金沙江堵塞形成堰塞湖,经计算被铲刮岩土体体积约240×104m3,第一次滑坡总方量为2 200×104m3,堆积体的最大厚度约为81.4 m[图3(a)]。堰塞坝于2018年10月12日自然溢流,堰塞湖水位逐渐降低,13日险情解除。
第二次滑坡事件在2018年11月3日发生,在第一次滑坡的影响下,滑坡后缘K1区失稳形成第二次滑坡,方量约为368×104m3的岩土体沿第一次滑坡形成的沟槽向下滑动,其运动过程中对坡面的铲刮作用携带坡面岩土体形成碎屑流,再次堵塞金沙江,经计算被铲刮岩土体体积约312×104m3,包括滑源区岩土体、被铲刮携带的岩土体以及第一次滑坡残留在坡体上的松散堆积体,第二次滑坡的总方量为850×104m3,堆积体的最大厚度约为78.2 m[图3(b)]。堰塞坝于11月9日在人工干预下泄洪。
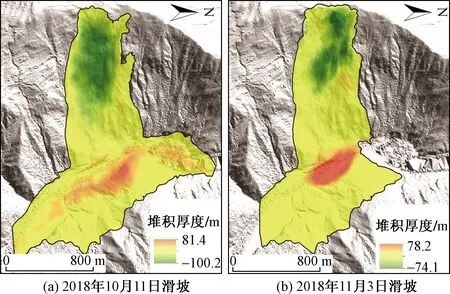
图3 滑坡堆积厚度图
2.3 滑坡潜在不稳定岩体特征
在第一次滑坡事件作用下,滑坡后缘及两侧三处潜在不稳定岩体[图2(a)K1、K2、K3区域][1]出现临空面为第二次滑坡事件提供了有利条件,第二次滑坡事件对其扰动后,根据现场监测结果显示三处潜在不稳定岩体仍然在持续变形[图2(b)],存在再次大规模下滑堵江的可能,因此后续通过数值模拟,对三处潜在不稳定岩体失稳做了预测研究。
3 白格滑坡数值模拟分析
3.1 MassMov2D模型描述
该模型的建立是基于Savage-Hutter理论,该理论假定流体为一种具有流变特性的单相均质材料。使用流动力学方程的深度积分的近似,将流动建模为2-D连续介质,这是泥石流数值模拟的常用方法[20-21]。与使用地形相关的局部参考系的深度积分模型不同,MassMov2D的控制方程在笛卡尔坐标x、y的二维欧几里得空间中被参考[22]。质量和动量平衡方程为
(1)
(2)
(3)
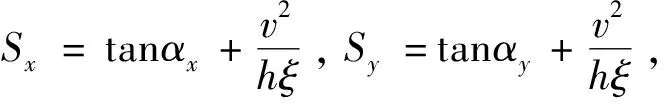
(4)
(5)
根据朗肯理论中主动和被动两个极值之间的范围可知ka≤1≤kp,其取值由碎屑流混合物的内摩擦角δ决定。
模型使用Voellmy模型,其库仑摩擦阻力增加了湍流分量,该湍流分量与湍流因子(ξ)和流动质量的厚度成反比,并且与流动速度的平方成正比[23]。模型通过以下关系描述:
(6)
式(6)中:τ为抗剪切应力;g为重力加速度;v为滑体的运动速度;ρ为滑体的密度;f为摩擦系数;ξ为湍流系数。
3.2 滑坡模型参数取值
模拟采用Voellmy模型,当湍流系数ξ的值很高时,湍流分量相对非常小,流变模型就缩减为库伦模型[24]。模拟采用的参数在表1中给出,模拟使用5 m精度的数字高程模型,模型运行时间步长约束为Δt≤1 s。
3.3 模拟结果分析
3.3.1 10月11日第一次滑坡事件模拟
由表1的参数对金沙江第一次滑坡事件进行模拟,分别选取10、20、30、60、80、100 s的运动过程的速度图(图4)、滑坡堆积厚度(图5)及滑坡堆积厚度曲线(图6)用来解释其运动过程。
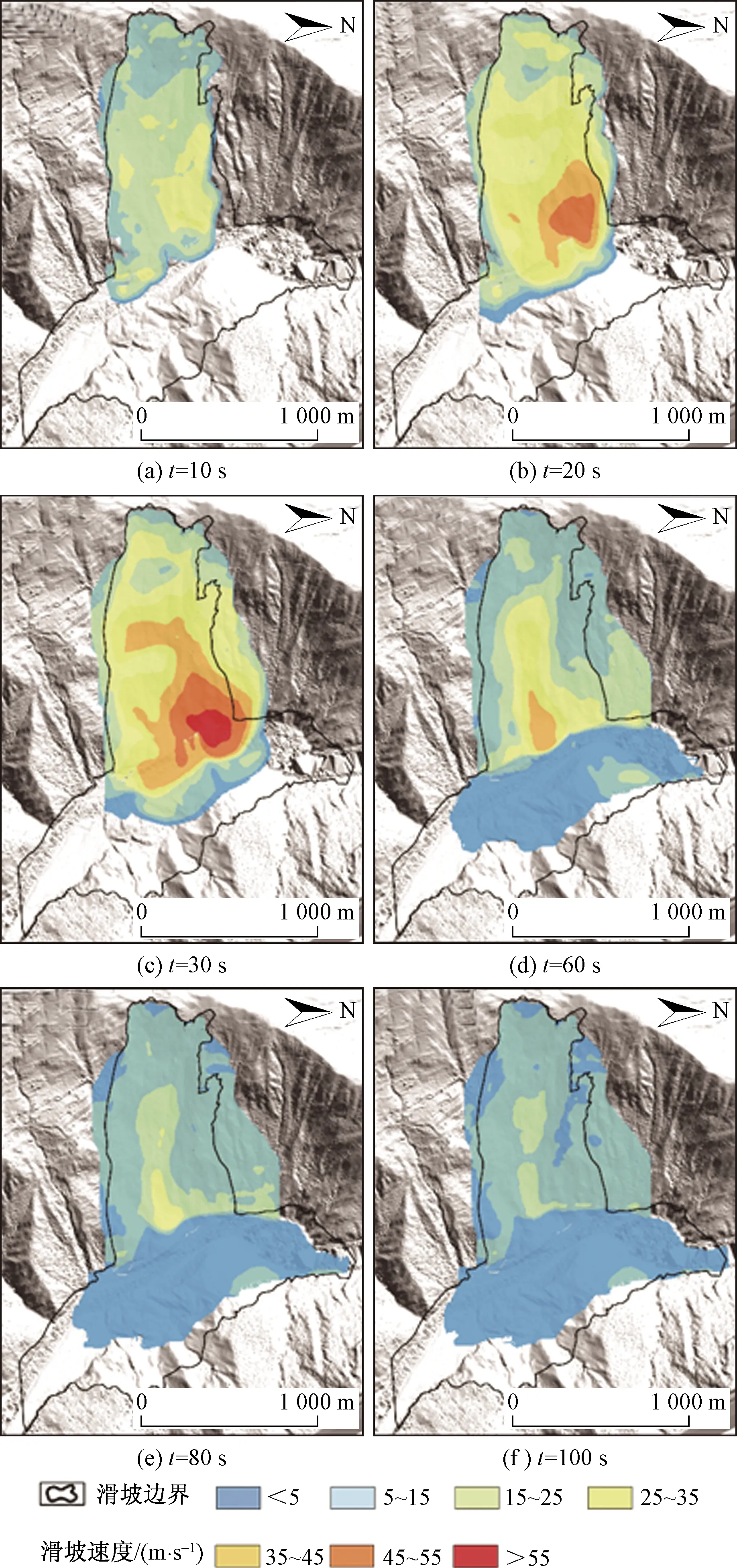
图4 第一次滑坡事件模拟运动过程速度
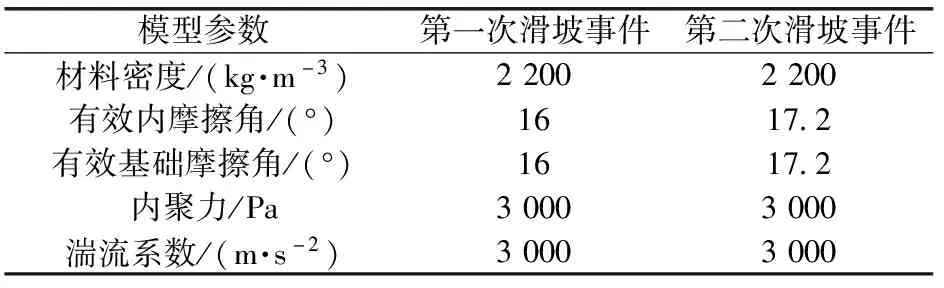
表1 模型参数取值表
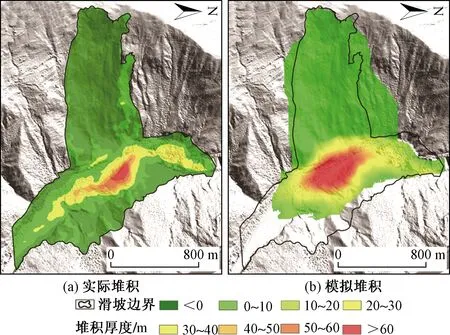
图5 第一次滑坡事件堆积厚度
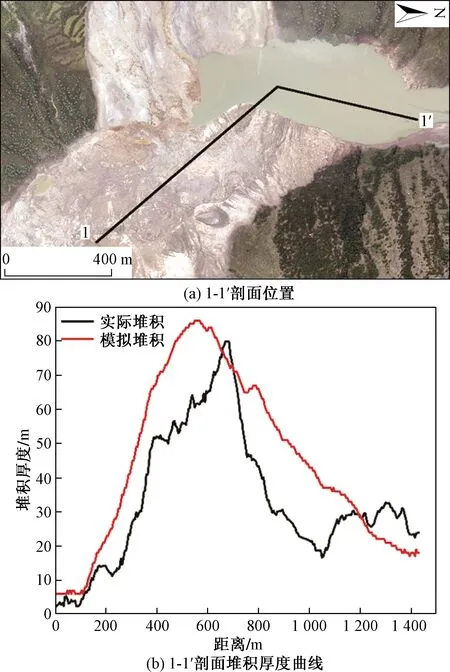
图6 第一次滑坡事件堆积厚度曲线图
第一次滑坡滑源区以及运动过程中铲刮作用携带的岩土体总量约2 200×104m3,设置好滑源区碎屑流体进行模拟。从图5中可以看出,滑坡形成的碎屑流体很快的向下运动,于30 s时运动速度达到最高值为69 m/s,30~60 s滑坡速度逐渐减小,100 s时第一次滑坡事件结束。
第一次滑坡事件堆积体形态、堆积厚度集中区域均与实际情况较为相似(图6),第一次滑坡堆积情况在1-1′剖面中680 m处为最大堆积厚度达79.8 m,模拟堆积情况在1-1′剖面中560 m处为最大堆积厚度达86 m,堆积曲线整体上趋势较为一致,模拟结果结合实际情况是在滑坡发生过程中有部分岩土体在江水冲刷带到下游,模拟过程没有考虑这一因素,故堆积厚度大于实际情况。
3.3.2 11月3日第二次滑坡事件模拟
由表1 的参数对金沙江第二次滑坡事件进行模拟,分别选取10、20、30、60、80、100 s的运动过程的速度图(图7)、滑坡堆积厚度(图8)及滑坡堆积厚度曲线(图9)用来解释其运动过程。
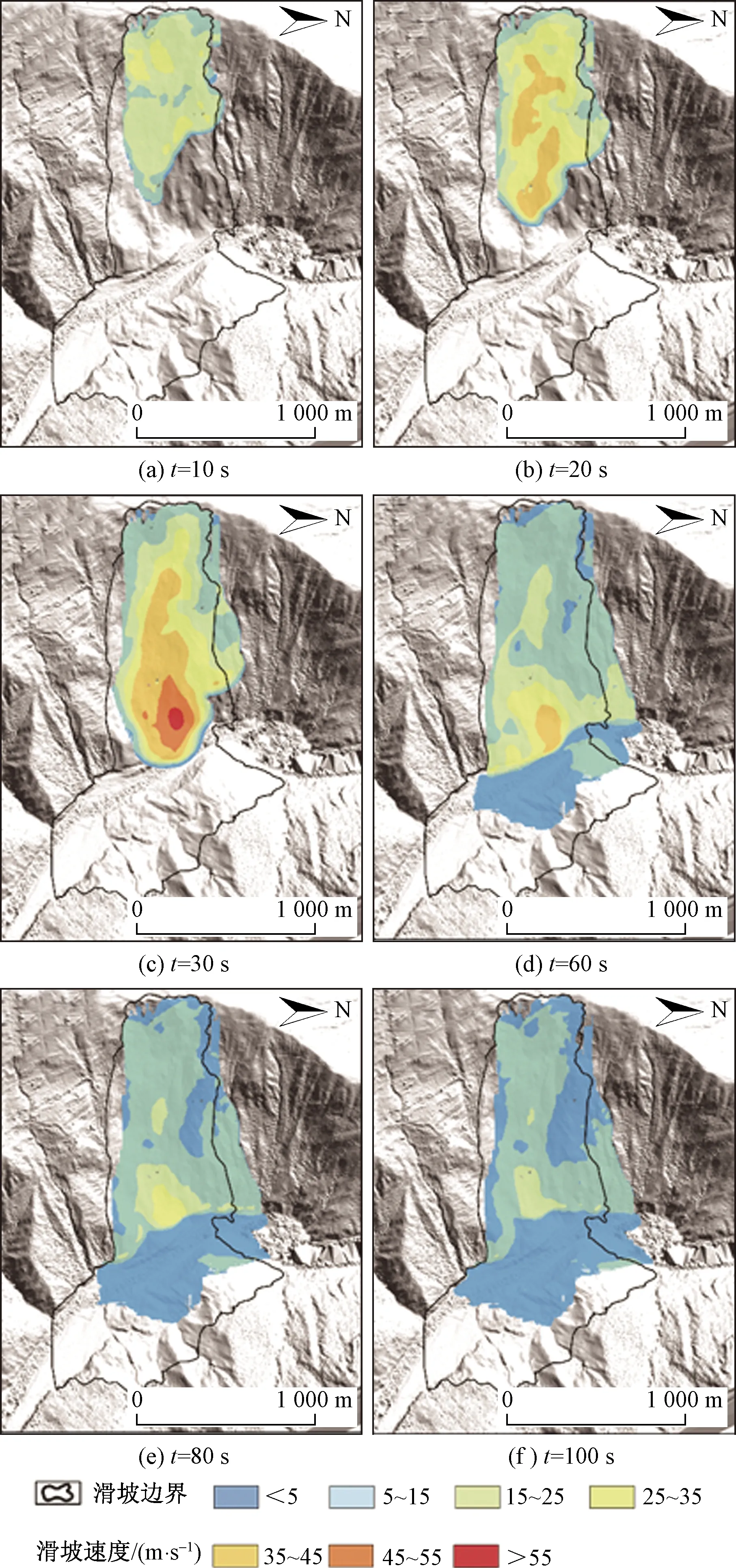
图7 第二次滑坡事件模拟运动过程速度图
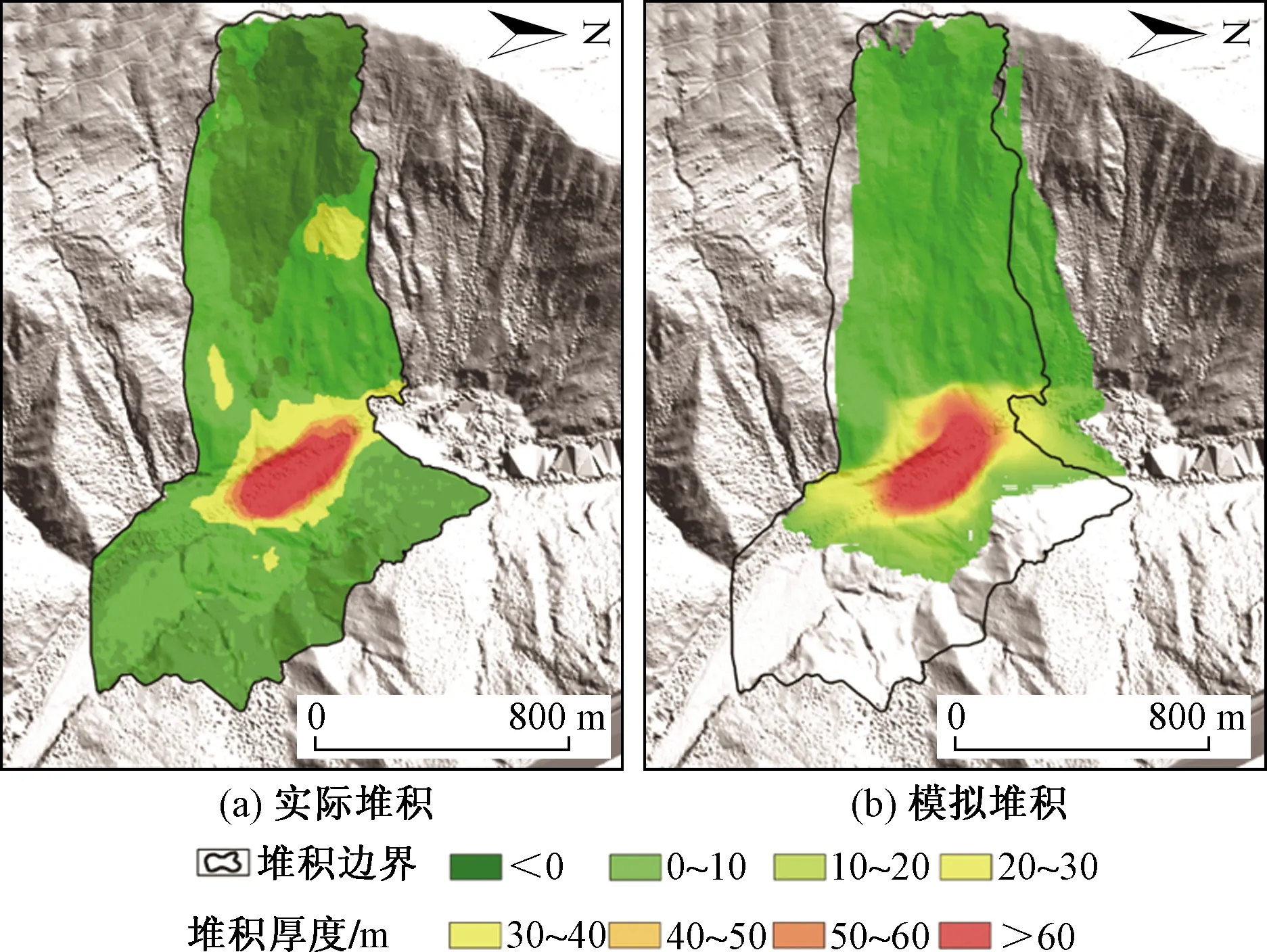
图8 第二次滑坡事件堆积厚度
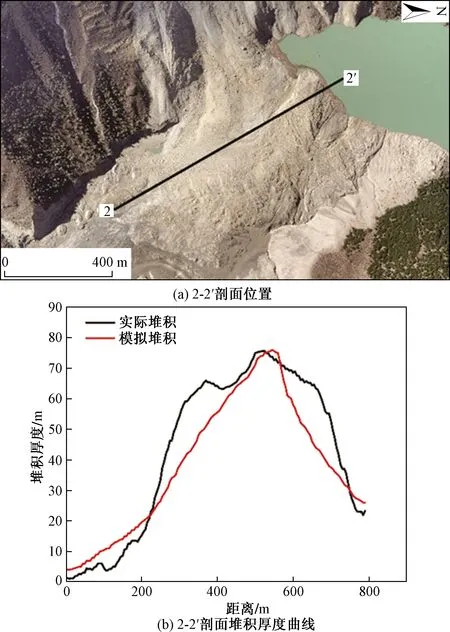
图9 第二次滑坡事件堆积厚度曲线图
第二次滑坡是由于K1区岩土体失稳,滑源区岩土体加上滑动过程中铲刮岩土体总方量为850×104m3进行模拟。从图7中可以看出,滑坡形成的碎屑流体沿第一次滑动形成的沟槽向下运动,速度慢于第一次滑坡事件,于30 s时运动速度达到最高值为58 m/s,30~60 s滑坡速度逐渐减小,100 s时第二次滑坡事件基本结束。
第二次滑坡事件堆积体形态、堆积厚度集中区域均与实际情况较为相似(图5),第二次滑坡堆积情况在2-2′剖面中525 m处为最大堆积厚度达75.7 m,模拟堆积情况在2-2′剖面中530 m处为最大堆积厚度达76 m,堆积曲线整体上趋势较为一致,堆积厚度最大区域匹配较好。
4 潜在不稳定岩体预测
前文中提到两次滑坡事件后,根据现场监测结果显示滑坡后缘及两侧有三处潜在不稳定岩体[图2(b)],存在再次发生滑坡的可能[1],因此对这三处潜在不稳定岩体进行模拟,使用第二次滑坡模拟反演得到的参数,预测其发生滑坡的运动速度、路径以及堆积范围和堆积厚度。
按照上述方法建立模型进行模拟,考虑三处潜在不稳定岩体同时滑动,整个运动和堆积过程持续约120 s。在30 s时滑坡速度达到最大值57 m/s,60~80 s滑坡速度逐渐降低,120 s时滑坡运动堆积过程基本结束(图10)。通过120 s时滑坡堆积厚度最大为64 m。金沙江白格两次滑坡事件最大堆积厚度分别为81.4 m和78.2 m,两次滑坡事件均造成堵江。通过数值模拟得到的堆积厚度和形态来看,如果三处潜在不稳定岩体同时下滑会再次形成堰塞体堵塞金沙江,此次模拟结果可为白格滑坡的防灾提供参考依据。
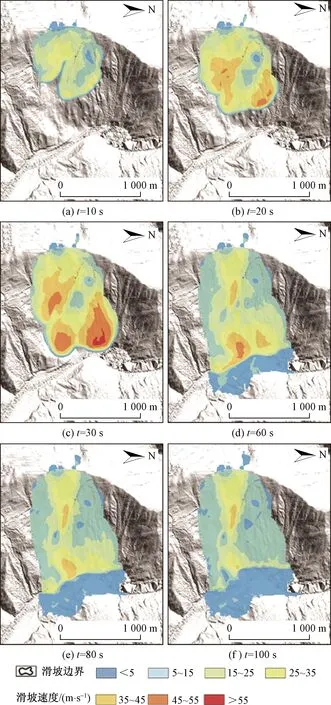
图10 潜在不稳定岩体模拟运动过程速度图
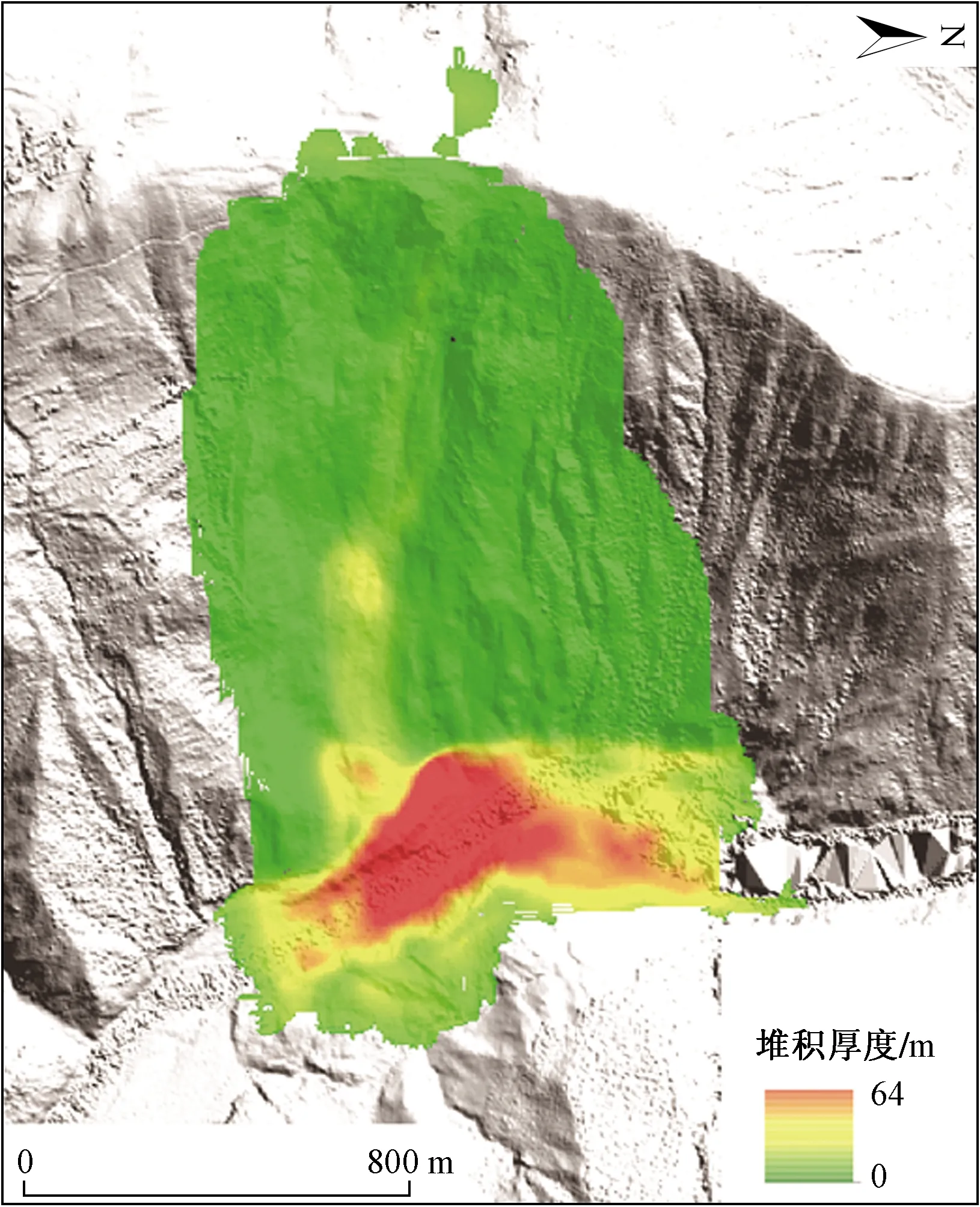
图11 潜在不稳定岩体预测滑坡堆积厚度
5 结 论
2018年10月11日和11月3日在金沙江发生两次滑坡事件,通过在PCRaster环境下使用MassMov2D模型对两次滑坡进行了模拟,得到以下结论。
(1)通过MassMov2D模型模拟金沙江白格两次滑坡运动过程和堆积特征,结果显示,第一次滑坡事件实际堆积最大厚度为81.4 m,模拟堆积最大厚度86 m;第二次滑坡事件实际堆积最大厚度78.2 m,模拟堆积最大厚度76 m,结果同真实情况较为接近。
(2)通过两次滑坡反演得到的参数,用于对三处潜在不稳定岩体的失稳预测,预测结果显示,三处潜在不稳定岩体同时失稳会形成滑坡,再次堵塞金沙江,堆积厚度达到64 m,因此应在滑坡区布设监测设备,实时监测三处潜在不稳定岩体变形情况,同时采取相应的防治措施治理。
(3)通过对两次滑坡事件数值模拟分析和潜在不稳定岩体预测,说明MassMov2D可以较好地用于碎屑流滑坡的研究和分析,研究结果可为研究区灾害防治提供一定的参考依据。

