基于Fluent旋转阀阀口流场分析

(1.江阴兴澄特种钢铁有限公司， 江苏 江阴 214400；2.北京机械工业自动化研究所有限公司， 北京 100120)

引言

旋转阀作为流体方向控制元件，应用在能源行业、化工行业及液压行业[1-2]。可以通过一个转动部件来接通或切断流体，具有可调范围宽、流通能力强、抗气蚀等优点，比直行程阀开关迅速，在间歇过程工业中得到广泛的应用[3]。

目前，旋转阀特性和应用研究较多。李少伟等[4]对脉冲萃取柱的空气脉冲旋转阀产生的空气脉冲过程进行了研究，将分析结果与大型空气脉冲旋转阀产生的脉冲压力进行了对比分析，结果一致，验证了模型的可靠性。李小彭等[5]设计了桩机用五口旋转阀模型，利用周期振动激励规律，建立AMESim模型分析旋转阀各参数对系统动态性能和沉桩的影响，并通过实验验证了模型的正确性和可行性。张鹏[6]设计了水液压旋转阀，并以此为模型进行阀口流场分析，得到不同流体参数下的分析结果，为后续试验样机试验提供了数据参考。周建明[7]通过对旋转阀工作原理及常见问题分析，找到了旋转阀床层步进显示故障的原因，保障了旋转阀的平稳运行。魏俊等[8]采用CFD仿真技术基于端面密封式旋转阀，研究了旋转阀结构参数对脉冲压力的影响，对水力振荡器的研究具有重要参考价值。

旋转阀的流体流动特性对旋转阀的工作特性有着关键的影响，本研究利用CFD[9]，对旋转阀阀口进行流场分析，初步探究旋转阀在不同开口度下的流体流动特性，为旋转阀阀口结构及流道优化改进提供参考。

1 旋转阀的工作原理

旋转阀的三维模型及工作截面如图1所示。阀芯旋转不同角度，工作油口有所差别。当阀芯旋转角度为0°～45°时，压力油口P与工作油口A接通，工作油口B与回油口T接通；当阀芯旋转角度为-45°～0°时，压力油口P与工作油口B接通，工作油口A与回油口T接通。基于上述原理，旋转阀可实现执行机构的间歇动作。

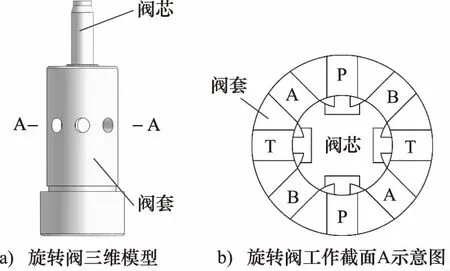
图1 旋转阀三维模型及工作截面示意图

2 旋转阀流场仿真模型

2.1 流动控制方程

流体流动满足三大守恒定律，分别为质量守恒定律、动量守恒定律及能量守恒定律，分别可以数学描述为连续性方程、动量方程(N-S方程)和能量守恒方程[10]。因液压阀内的流动多为湍流，无法直接用上述定律求解，引入湍流模型可以有效解决[11]。旋转机械一般采用RNGk-ε模型，由于RNGk-ε模型中加入R项，因此比标准k-ε模型更能准确模拟快速剪切和涡旋流动，具体方程如下：

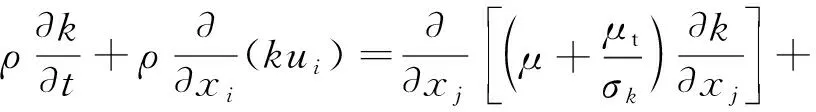
Gk+Gb-ρε-YM

(1)

(2)

(3)

式中，ρ—— 流体密度

k—— 单位质量流体湍流脉动动能

t—— 时间

xi，xi—— 坐标方向

ui—— 时均速度

μ—— 分子扩散造成的动力黏性

μt—— 湍流黏性系数

σk—— 脉动动能的Prandtl数

Gk—— 由于平均速度梯度引起的湍动能产生项

Gb—— 由于浮力影响引起的湍动能产生项

YM—— 可压缩湍流脉动膨胀对总得耗散率的影响

ε—— 单位质量流体湍流耗散率

S—— 广义源项

其中，C1ε,C2ε,Ck,C3ε,η0,Cμ,β为默认的常数，具体值为C1ε=1.42，C2ε=1.68，Ck=1.0，C3ε=1.3，η0=4.38，Cμ=0.09，β=0.012。

2.2 物理模型

根据设计参数，在SolidWorks中，分别建立3个不同旋转角度的旋转阀模型，然后导入ANSYS中抽取阀口流体域模型[12]。旋转阀为对称结构，阀口从打开到关闭，阀芯旋转45°。阀芯旋转到22.5°时，旋转阀过流断面面积最大，故分别选取阀芯旋转角度11.25°，22.5°，33.75°进行建模分析。如图2为不同旋转角度的流体三维模型。

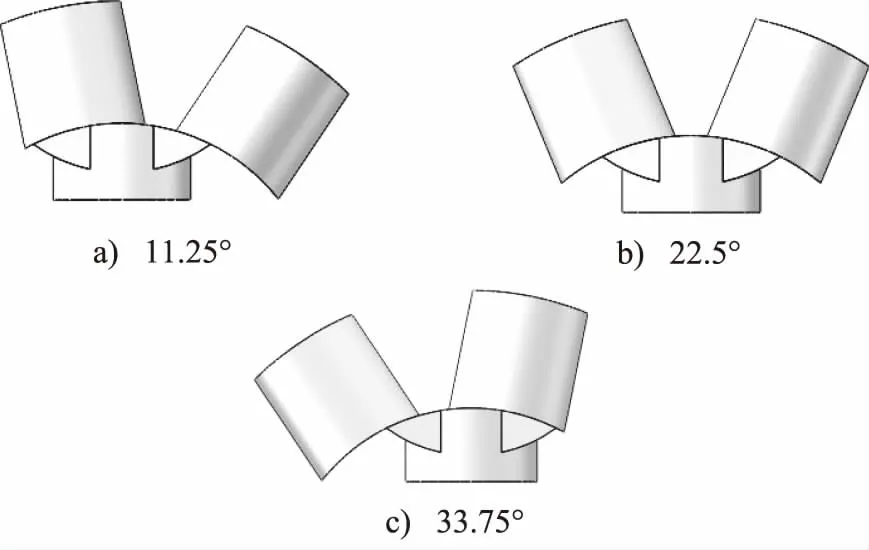
图2 不同旋转角度旋转阀阀口流场模型

2.3 网格模型

将SolidWorks三维模型导入ANSYS Workben-ch中进行网格划分，选择四面体单元进行体网格划分，单元总数为37247。同时，检查网格质量，对质量较差的网格进行修改，从而保证计算结果的准确性[13]。如图3所示为旋转阀阀口流体网格模型。

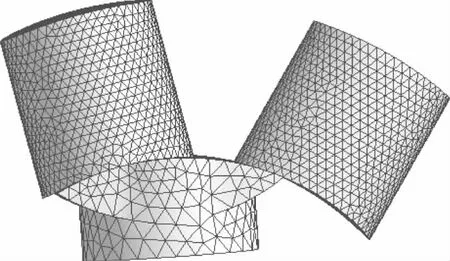
图3 旋转阀阀口流体网格模型

2.4 边界条件

本研究利用Fluent软件进行仿真分析，在其中进行如下边界条件设置：

(1) 旋转阀为理想模型，不考虑间隙泄漏；

(2) 流体介质采用航空10号液压油，密度取870 kg/m3，动力黏度为0.0087 kg/(m·s-1)，流体不可压缩，且流体经过阀口时速度大时间短，来不及与外界进行热交换，可认为此过程为绝热过程；

(3) 入口为流速入口，6.4 m/s；出口为压力出口，11 MPa。壁面为光滑无滑移绝热壁面；

(4) 旋转阀阀口通径为8 mm，考虑入口流速，计算流体雷诺数为5151.7>4000，阀内流体流动状态为湍流，采用RNGk-ε湍流模型进行后续分析。

3 旋转阀流场仿真分析

3.1 阀芯旋转11.25°阀口仿真分析

当旋转阀阀芯旋转11.25°时，旋转阀进口过流断面面积大于出口过流断面面积，流体从左侧进油口进入旋转阀内，并由右侧出口流出，阀口内流体速度分布、压力分布和流速矢量图，如图4所示。

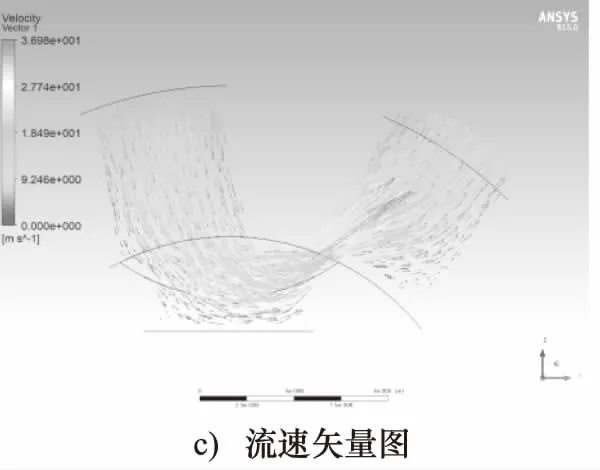
图4 阀芯旋转11.25°流体流场

从流体速度云图和流速矢量图可以看出，流体从阀进口流入旋转阀，而后经过阀芯的反射，从阀出口流出。同时因为流体的黏性作用， 从通道壁面到通道中心，速度呈梯度变化，近壁面流速为0。由于阀出口过流断面突然减小，该位置处速度较高，形成射流，最大可达37 m/s。从流体压力云图可以看出，因为阀出口的过流断面突然减小，局部压力损失较大，约为2.1 MPa，旋转阀总压差约为3.7 MPa。

3.2 阀芯旋转22.5°阀口仿真分析

当旋转阀阀芯旋转22.5°时，旋转阀进出口过流断面面积大小相等，流体流向与3.1相同，阀口内流体速度分布、压力分布和流线图，如图5所示。

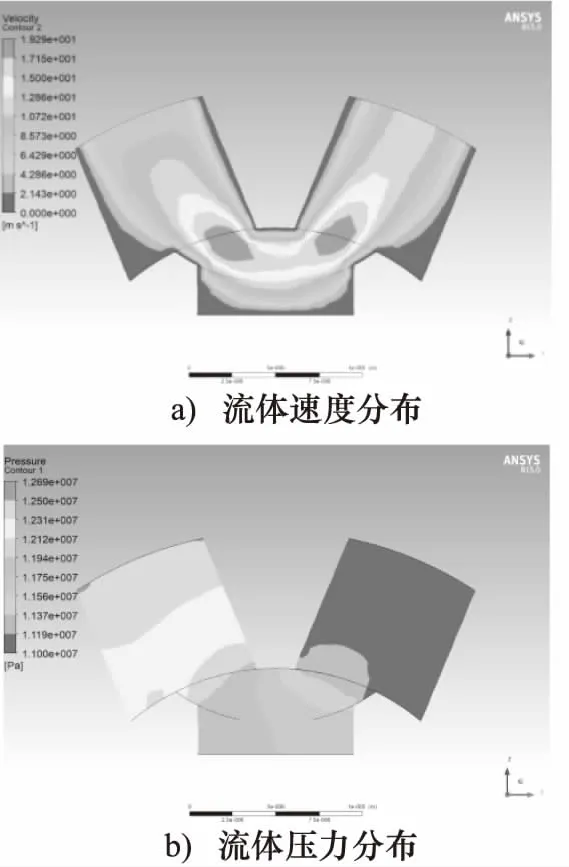
图5 阀芯旋转22.5°流体流场

从流体速度云图和流速矢量图可以看出，流体因阀芯旋转角度的变化，射流角度也发生改变，此时阀进口和出口都形成射流。同时，由于阀进出口过流断面大小相等，两位置处速度相同，最大可达约19 m/s。从流体压力云图可以看出，阀进口过流断面减小，出口过流断面增大，局部压力约为0.7 MPa左右，旋转阀总压差约为1.5 MPa。

3.3 阀芯旋转33.75°阀口仿真分析

当旋转阀阀芯旋转33.75°时，旋转阀进口过流断面面积小于出口过流断面面积，流体流向与3.1相同，其阀口内流体速度分布、压力分布和流线图，如图6所示。

图6 阀芯旋转33.75°流体流场

从流体速度云图和流速矢量图可以看出，流体因阀芯旋转角度的变化，使阀进口过流断面突然减小，在阀进口形成射流，该位置处速度较高，最大可达约39 m/s。从流体压力云图可以看出，因为阀进口的过流断面突然减小，局部压力损失较大，约为2 MPa，旋转阀总压差约为3.8 MPa。

3.4 不同旋转角度旋转阀特性分析

当旋转阀阀芯分别旋转11.25°，22.5°，33.75°时，旋转阀过流断面面积跟随变化，流体经过旋转阀，其压力也有所变化，过流断面变化及压差变化曲线，分别如图7、图8所示。

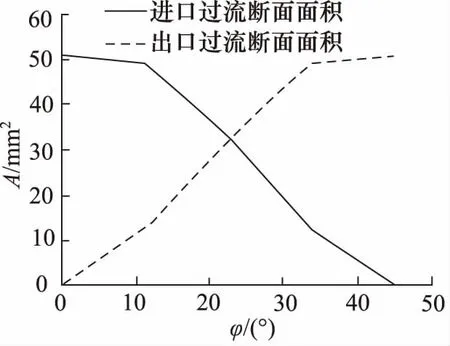
图7 不同旋转角度过流断面面积变化

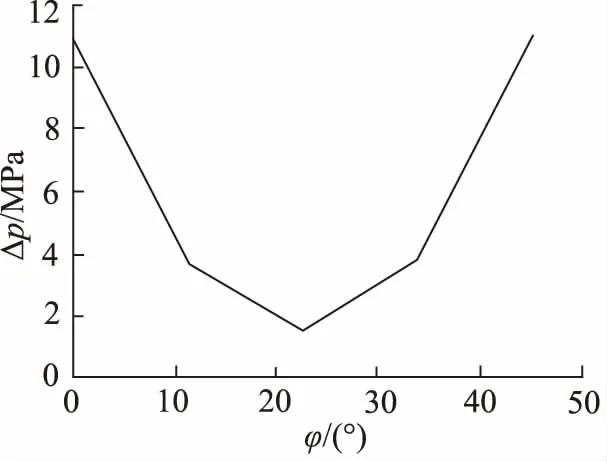
图8 不同旋转角度旋转阀压差变化曲线

从图中可以看出，当旋转阀阀芯旋转角度由11.25°增大至22.5°时，旋转阀过流断面面积由小变大，流体局部压力损失减小，总压差由3.7 MPa减小至1.5 MPa。当旋转阀阀芯旋转角度由22.5°增大至33.75°时，旋转阀过流断面由大变小，流体局部压力损失增大，总压差由1.5 MPa增大至3.8 MPa。

4 结论

通过利用RNGk-ε模型对旋转阀3种阀芯旋转角度下的阀口流场进行仿真，得到了旋转阀阀进出口的速度、压力分布及速度矢量图，为旋转阀设计改进提供参考。经分析得出以下结论：

(1) 当阀进口过流断面面积增大时，出口过流断面面积减小；当阀进口过流断面减小时，出口过流断面面积；进口节流或出口节流都会造成较大的压力损失。当阀芯转至22.5°时，即阀进口与阀出口过流断面面积相等，压力损失最小；

(2) 流体经阀进口流入旋转阀，而后经过阀芯的反射，从阀出口流出。流体的射流位置和角度因旋转阀旋转角度不同而不同。