Adaptive Output Regulation of a Class of Nonlinear Output Feedback Systems With Unknown High Frequency Gain
Yuan Jiang and Jiyang Dai
Abstract— This paper presents an output feedback design approach based on the adaptive control scheme developed for nonlinearly parameterized systems, to achieve global output regulation for a class of nonlinear systems in output feedback form. We solve the output regulation problem without the knowledge of the sign and the value of the high frequency gain a priori. It is not necessary to have both the limiting assumptions that the exogenous signal ω and the unknown parameter μ belong to a prior known compact set and the high frequency gain has a determinate lower and upper bounds. The effectiveness of the proposed algorithm is shown with the help of an example.
I. Introduction
IN this paper, we consider the problem of global output regulation for nonlinear systems of the form as follows:
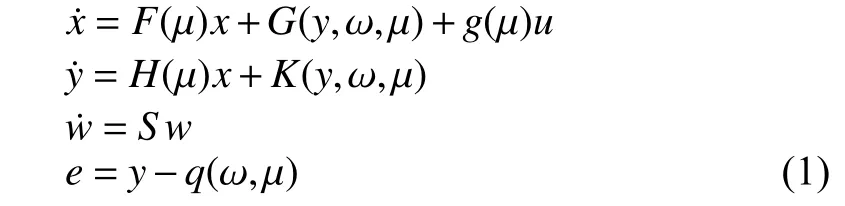
The first global output regulation problem of (1) was reported in [1]. However, the paper assumes that the exogenous signaland the unknown parameterbelong to a prior known compact set. This is a limiting assumption, as the controller should also be changed as the bounds of exogenous signal are changed. In [2], an adaptive output regulator was proposed based on the adaptive control method developed for nonlinearly parameterized systems in [3], [4], which achieves global output regulation of the nonlinear system (1) without requiring the knowledge of the bounds of the unknown parameters and exogenous signals. However, [2] assumed that the sign of the high frequency gainis known. In this case,when the sign ofis unknown, the method developed in[2] is not applicable anymore. In this paper, we will consider the same problem with the unknown high frequency gain i.e.,both the sign and value of control coefficient is assumed to be unknown.
Note that, the work dealing with the global robust output regulation in the output feedback form with the unknown control directions is reported [5] with the assumption that the high frequency gain has a determinate lower and upper bounds. In fact, an exterior unknown bounded parameter is used to regulate the control direction. Therefore, a natural and meaningful problem is how to design the controller without the knowledge of the bounds of the unknown high frequency gain. In this paper, we will use the backstepping, adaptive control technique and Nussbaum gain methods to design a nonlinear output feedback controller. Finally the simulation shows that the proposed nonlinear output feedback controller ensures the boundedness of all the states of the closed loop system and the tracking error asymptotically converges to zero. The approach we use here is an integration of the robust stabilization technique, adaptive technique and backstepping technique.
II. Preliminaries
Lemma 1 [6]:Letandbe smooth functions, andbe an even Nussbaum function in [7]. If the following inequality holds, i.e.,

In the following we will make assumptions that have been commonly used when dealing with output regulation of nonlinear systems in the output feedback form.
Assumption 1:System (1) has a uniform relative degree
Assumption 2:For system (1), the high frequency gain
Remark 1:Assumption 2 indicates that the sign of the high frequency gainis unknown. In our paper, we also assume that the value of the high frequency gainis unknown.References [1], [2], [8], and [9] assumed that the sign of the high frequency gainis known. In this case, when the sign ofis unknown, the method developed in [1], [2], [8], and[9] is not applicable anymore. Here, it is also not necessary to have the assumption that the high frequency gain has a determinate lower and upper bounds.
Assumption 3:For every µ ∈ ℘, the linear systemis minimum phase.
Remark 2:Under the Assumption 3, the linear systemis minimum phase. Together with Assumption 1, this implies that Assumption 3 is essentially equivalent to the condition that the matrixis Hurwitz with the restrictionThis is exactly the assumption which is used in [10] and [11], where the global stabilization problem was studied.
Assumption 4:There exist globally defined smooth functionsandsatisfying the regulator equations

It has been shown in [12] and [13] that there exists a parameter dependent filter transformation such that system (1)can be introduced in a lower triangular form. Indeed,introducing the filter

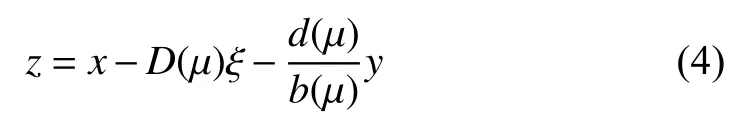
Using (3) and (4), (1) can be transformed into

Remark 3:It is easy to conclude thatis a Hurwitz matrix for allin [14].
As pointed in [1] and [8], [9], the problem of output regulation can be transformed into a stabilization problem under suitable conditions. We use the method introduced in[8] to perform such a transformation under the following hypothesis.
Assumption 5:Suppose thatdefined in Assumption 4 is a trigonometric polynomial of the form

Remark 4:As shown in [8] and [15], Assumption 5 implies the existence of a globally defined mappingand a set of real numbers,satisfying

It can be shown that all the eigenvalues ofare simple and located on the imaginary axis as in [7], [8], [15]–[17].
Under Assumption 5, for any Hurwitz matrixandwhereis controllable, the Sylvester equationhas a unique solutionwhich is nonsingular.Then, we can define a dynamic system of the form

as an internal model for system (5).
Now, we are ready to transform the output regulation problem to a stabilization problem via a global change of coordinates. Using the following change of coordinates

gives the following triangular form

where
The objective of this paper is to find a smooth dynamic output error feedback adaptive stabilizing controller
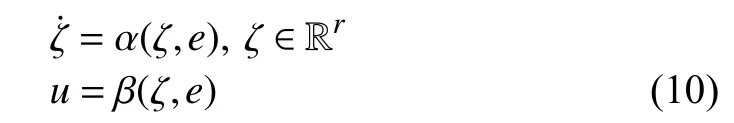
such that the closed loop system (9) is globally bounded for any initial conditionand anywhile the errorasymptotically converges to zero.
Remark 5:is called the control coefficient in this paper,which is considered to be unknown, if both the sign and value are unknown. If system (9) is globally asymptotically stabilized by output error feedback, the same controller also solves the global output regulation problem for the original system (1).
Remark 6:By construction,is a Hurwitz matrix.Therefore, there exists a matrixsuch that
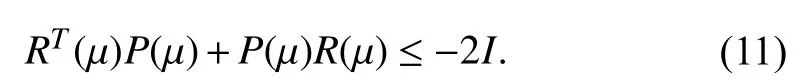
III. Main Result
In this subsection, we will consider the global robust stabilization problem of the system (9). When the sign of the control coefficientis known, the global stabilization problem of system (9) has been solved in [2]. In the absence of the assumption on the control coefficient sign, the method in [2] is no longer applicable. Then, we combine this method with the Nussbaum gain method to solve the same problem with the unknown control coefficient.
Let us first introduce some inequalities that will be used later. Recall that bothandare in compact sets whose bounds are unknown. According to Lemma in [3], [4], and[18] we have


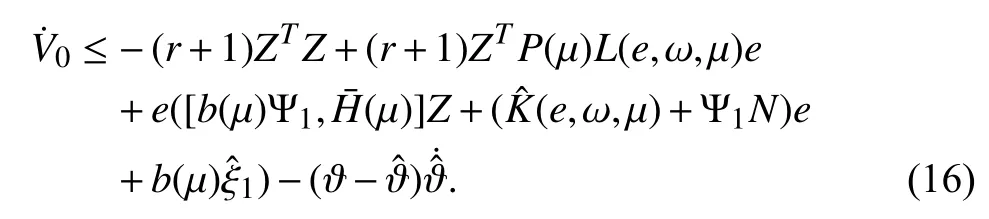
For the second and third term, by the aforementioned inequalities (12), (13) and (14) and the completing of squares,we have

Substituting (17)–(19) into (16), we conclude that
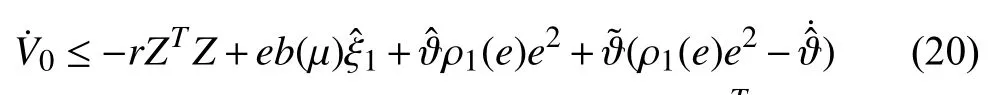


Substituting (21) into (20), and after some algebraic manipulation, we have

Step 1:Choose Lyapunov function candidate


By (13), (14) and the completion of squares, it is easy to obtain

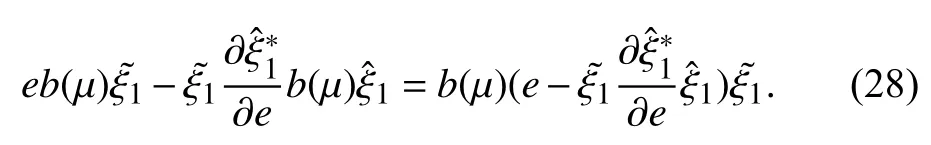
Then, from the aforementioned definition ofsubstituting(26)–(28) into (25), we can obtain

So we can choose the smooth virtual controller
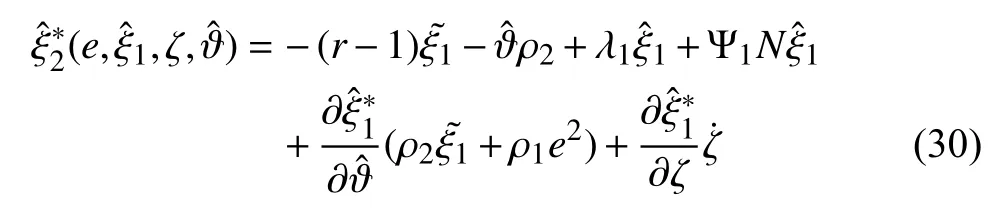
which renders

Step 1 is thus completed. The remaining steps can be recursively executed.
Inductive Step:Assume that there exists smooth, positive definite and proper Lyapunov function candidatescorrespond torespectively,andsatisfy the following inequality

In the following sections, we prove that (32) holds as well as in step
Choose the Lyapunov function candidate


Using an argument similar to the ones in the previous step,we can obtain

Therefore, we choose the smooth virtual controller

From (36), it is clear thatcan be expressed as the
Substituting (36) into (35), and after some algebraic manipulations, it implies

Using the inductive argument, it is reasonable to conclude that at stepthere exists a smooth, positive definite and proper Lyapunov function candidateand a smooth controllerwithsatisfying the following inequality

Therefore, the actual controller and the adaptive law are obtained and given by

leading to

Thus, we have completed the design procedure of the output error feedback adaptive control using backstepping and tuning function techniques. In the following we will prove that all the states of the closed loop system are bounded for alland the tracking errorconverges to zero asWe first assumed thatfor someis the maximal internal of existence of the solution of the closed loop system and letApplying lemma 1 to inequality(40) shows thatandare bounded onSinceis a positive definite quadratic function inthe variablesmust be bounded onTherefore,no finite time escape phenomenon may happen andmeaning thatare bounded for allAs a result, all closed loop system states are bounded for allAlso,are bounded for allFurthermore, integrating (40) fromshowsare square integrable onBy Barbalat's lemma,approaches to zero asTherefore, the tracking error converges to zero asymptotically.
The result of this section is summarized in the following.
Theorem 1: Considering that system (1) satisfies Assumptions 1–5, then the introduction of the observer (3)and the internal model (7) in conjunction with (21) and (39)into system (1) ensures that global output regulation of the uncertain system (1) is achievable by an error feedback controller.
IV. An Example
We consider the planar system with the three-dimensional exosystem

It can be verified that the solution of the regulator equation of this system exists globally and is given by=thus Assumption 4 is satisfied.
Therefore, following the design procedure developed in the previous Section III, an output feedback controller which solves the global output regulation problem for system (41)can be given by

where

In the simulation, the initial condition are set to bethe reference signaland the disturbance signalFig. 1 gives the error output which converges to zero. Fig. 2 and Fig. 3 show that all the states of the closed loop system are bounded. Fig. 4 shows that the parameter estimatesandare bounded.
V. Conclusion

Fig. 1. Transient response of the error signal.

Fig. 2. Transient response of the states
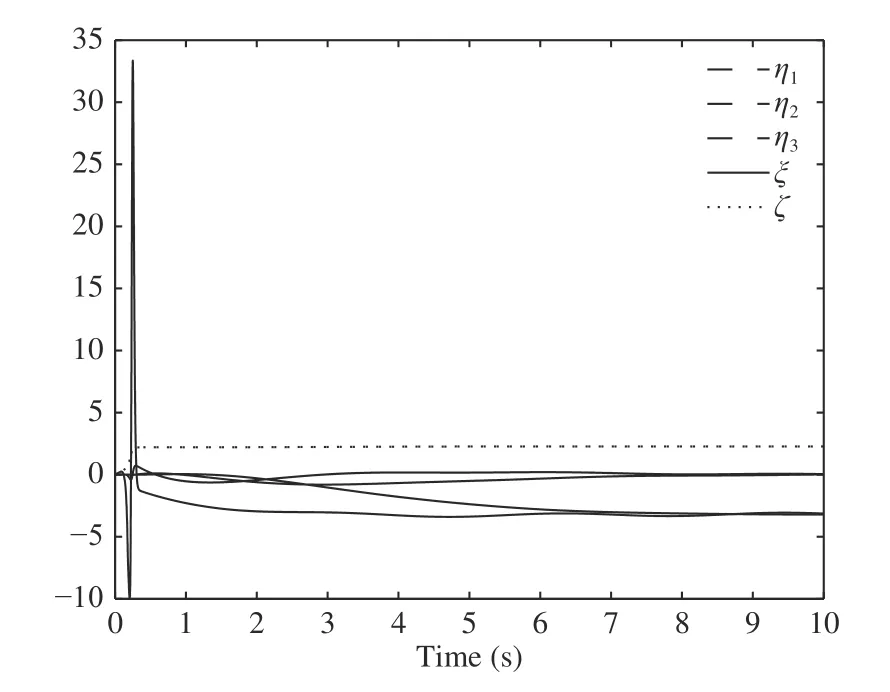
Fig. 3. Transient response of the states

Fig. 4. Parameter estimates and
This paper presents an output error feedback design approach based on the adaptive control scheme developed for nonlinearly parameterized systems, to achieve global output regulation for a class of nonlinear systems in output feedback form. We solve the output regulation problem without the a priori knowledge of the sign and value of the high frequency gain. In our work it is not necessary to have the limiting assumption that the exogenous signaland the unknown parameterbelong to a prior known compact set and also have the assumption that the high frequency gain has a determinate lower and upper bounds. Recently, several exciting breakthroughs have been made for the stochastic nonlinear systems, for instance, global stabilization [22], [23]and output tracking [24] have been solved. However, there are lesser results available in the literature addressing the output regulation problem [25], [26]. It is interesting to further consider the output regulation problem of the stochastic nonlinear systems.
 IEEE/CAA Journal of Automatica Sinica2020年2期
IEEE/CAA Journal of Automatica Sinica2020年2期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Parallel Reinforcement Learning-Based Energy Efficiency Improvement for a Cyber-Physical System
- Flue Gas Monitoring System With Empirically-Trained Dictionary
- Post-Processing Time-Aware Optimal Scheduling of Single Robotic Cluster Tools
- Unified Smith Predictor Based H∞ Wide-Area Damping Controller to Improve the Control Resiliency to Communication Failure
- Optimal Neuro-Control Strategy for Nonlinear Systems With Asymmetric Input Constraints
- A Method for Deploying the Minimal Number of UAV Base Stations in Cellular Networks
