渤海海峡沉积物输运的参数化计算

齐富康，边昌伟，徐景平

(1.中国海洋大学 海洋地球科学学院，山东 青岛 266100；2.中国海洋大学 物理海洋教育部重点实验室，山东 青岛266100；3.南方科技大学 海洋科学与工程系，广东 深圳 518055；4.青岛海洋科学与技术试点国家实验室 海洋地质过程与环境功能实验室，山东 青岛 266061)

1 引言

渤海海峡是连接渤海和黄海两个陆架海区的唯一通道，其特殊的地理位置使其成为研究黄河入海物质输运、渤、黄海之间物质交换和泥质体形成等重要科学问题的关键[1-3]。渤海海峡悬浮物的输运主要受风和潮流的影响，输运方式包括平流输运和局地再悬浮[4-7]。水动力强弱影响着悬浮物的动力过程，当波浪扰动影响到海底时，波流耦合会增强底剪切应力，从而更有可能造成海底沉积物的再悬浮[8]。受东亚季风季节性变化的影响，渤海海峡冬季水动力强度显著大于夏季，即冬季沉积物再悬浮作用明显，导致冬季悬浮物输运通量显著高于夏季[5,9]。

目前对渤海海峡的沉积物输运研究主要是基于物理模型和现场观测两种手段。现场观测研究开展稍晚而且观测方式主要是集中于走航和大面站的观测[1,6-7,10-11]，单点连续观测资料较少[5,12]。Martin等[1]依据观测数据得出渤海海峡南侧水平悬浮物通量（Suspended Sediment Flux，SSF）约为 11.9 Mt/a。Bi等[5]依据MODIS遥感数据和定点连续观测结果，计算的渤海海峡南侧SSF约为40.0 Mt/a。此外，Wang等[7]指出渤海海峡夏季悬浮物浓度（Suspended Sediment Concentration，SSC）垂向分布不均匀，并将SSC视为上下两层计算SSF，结果要比前人[5]结果大16%。综上所述，以往的SSF计算使用几个层位平均或全水深平均的SSC代表整个水体，忽略了底边界层（Bottom Boundary Layer，BBL）流速和SSC在垂向上的剧烈变化对结果的影响。此外，由于缺乏实测数据，尤其是底边界层沉积动力学观测资料，量化推移质输运及其在渤海海峡沉积物通量中的贡献存在困难。

利用基于观测数据的参数化计算方法可以增进对底边界层沉积物输运过程和机制的认识。以对流扩散方程为基础的垂向一维参数化模型在河口和海岸悬浮物剖面研究中有着广泛的应用[13-16]。以往一维参数化模型大多假设浓度剖面是Rouse分布或者其变异形式[8,17-18]，忽略了SSC的分层效应和底质泥沙颗粒粒度分级的影响。虽然沉积物浓度分层在河流或浅水地区不明显，但是在较深水中忽略分层效应会对模拟的浓度剖面产生重要影响[19-20]。此外，细颗粒泥沙的黏性作用会阻碍泥沙起动。在黏性颗粒占到一定比例的区域，忽略底质泥沙颗粒粒级多样性而使用中值粒径代表底质进行再悬浮浓度剖面计算的有效性有待验证。

综上所述，为了探讨底边界层沉积物输运的重要性，本文结合观测资料，确定了最优的沉积物输运一维参数化方案，计算了渤海海峡冬季底边界层SSC剖面分布，比较了参数化计算底边界层SSC与用定值代替底边界层SSC这两种情况下底边界层SSF计算结果的差异，最终量化了研究海区的SSF和推移质输运。

2 研究区域概况

渤海海峡指辽东半岛南端老铁山西南角至山东半岛蓬莱登州头一带水域，南北宽度约100 km，水深约20～80 m，是典型的陆架浅海区。庙岛群岛把渤海海峡分割成若干个水道，北端的老铁山水道是最重要的水道，最大水深86 m；南端为登州水道，水深约20～30 m[21]。海峡北部底质是砾石和裸露的基岩，中部和南部底质是相对细颗粒的沉积物，包括砂、砂质粉砂、粉砂、黏土质粉砂[22]。

早期研究表明渤海海峡的水通量呈现“北进南出”的格局，即黄海水流从渤海海峡北侧进入渤海，渤海的水流由南侧流入黄海[23-25]。Zhang等[26]依据不同季节的观测数据提出了渤海海峡海流运动的3种格局，“北进南出”的格局只出现在秋季和冬季。渤海海峡潮汐由M2分潮占主导，此外还有K1、S2等分潮，最大潮流流速在0.7～2.0 m/s之间[9,27-28]。潮汐方向大致呈现与海岸平行的东西向，涨潮流向西，落潮流向东。

3 观测数据与方法

3.1 数据资料

本文所用数据为2018年1月2-13日在渤海海峡T01和T02站（图1）获取的定点连续观测资料（表1）。为了图件时间的统一，本文将1月2日08:30定义为起始时刻，以1 h为间隔递增。

观测中使用包含波浪模块的声学多普勒流速剖面仪（ADCP）获取水体的流速剖面和波浪参数（波高、波周期等）。ADCP发声频率是614 kHz，采样间隔20 min，安装在底基平台上向上观测，传感器分别距底 1.55 m（T01）和 0.80 m （T02），层厚设置为 0.75 m。此外，于1月6日09:00到1月7日10:00，利用船基吊放的方式在两个站位同时进行了连续26 h、每小时一次的剖面观测并分层采水，搭载仪器有：采水瓶3个和现场激光粒度分析仪（LISST-200X）1台，采水层位分别是表层（水下1 m）、中层（0.4倍水深）和底层（距底约3 m），水样经抽滤、烘干、称重后计算得到实测悬浮物质量浓度（SSCp）。实验过程使用的滤膜直径为47 mm、孔径为0.45 μm。每个水样使用上下两层滤膜，下膜为对照组，用以校正实验过程中上膜的损失。

观测期间使用抓斗取样器获取海底表层样，并通过Malvern MS2000激光粒度仪进行粒度分析测试，得到样品的粒度频率分布（图1）。T01站中值粒径为139.8 μm，T02站中值粒径为91.2 μm。为了方便后续分粒级计算，本文将底质粒度分为8个组（表2）。此外，分析过程使用的风场数据来自NCEP气候预测系统版本 2（CFSv2）模拟结果（https://rda.ucar.edu/datasets/ds094.1/），时间间隔为 1 h。

3.2 ADCP声学信号反演悬浮物浓度

ADCP声学信号可以用于反演SSC，反演得到的悬浮体质量浓度SSCi与观测获得的反向散射等效电压Vrms相互关系可以写成如下形式[29]：

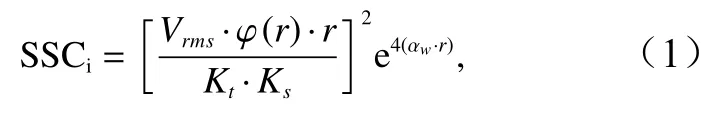
式中，Vrms=10Kc·E/20，Kc为转换系数，将散射强度的单位由count转化为dB，E为ADCP原始后散射强度；φ(r)为近场矫正因子，取决于测量点到换能器的距离、换能器的半径和信号波长[30]；r为测量点到换能器的距离；Kt为传感器灵敏度，是测量系统的固定参数；Ks为悬浮颗粒的散射特性参数，取决于颗粒粒径、颗粒分布模式以及悬浮颗粒的反向散射形式函数[31-32]；αw为海水吸收导致的信号衰减系数[33]。如果取观测期间海水各参数的平均值（温度为7℃、盐度为32、pH为8），计算得到的信号衰减系数为0.019 Np/m（1 dB=8.686 Np/m）。依据以上方法，本文在两个研究站位分别建立SSCi与SSCp的拟合关系（图2），发现均存在显著的正线性相关关系，且斜率接近1。因此，由ADCP回声强度反演得到的悬浮物质量浓度可以代表实际悬浮物质量浓度。

图1 观测站位（a）及其表层样的粒度频率分布（b，c）Fig.1 Observation stations (a) and particle size frequency distribution of bed sediments (b,c)

表1 两个站位基本信息和现场观测使用的仪器Table 1 The basic information of two stations and instruments used during in-situ investigation

表2 T01和T02站海底沉积物组分划分Table 2 Fractions of bed sediments of stations T01 and T02

3.3 剪切应力计算

颗粒的临界起动剪切应力作为海床沉积物起动的阈值，是表征沉积物抗侵蚀能力的重要指标。当底剪切应力大于临界起动剪切应力时海底沉积物发生再悬浮。

3.3.1 底剪切应力的参数化计算

本文的底剪切应力使用Soulsby[8]和Van Rijn[17]的模型分别计算并比较。

Soulsby[8]的底剪切应力模型计算浪-流合致平均底剪切应力（τm）和最大底剪切应力（τmax），

图2 ADCP回声强度反演的悬浮体浓度（SSCi）与抽滤实验得到的悬浮体浓度（SSCp）拟合Fig.2 Linear fitting equations between suspended sediment concentration estimated from ADCP echo intensity (SSCi) and suspended sediment concentration measured from pumping experiment (SSCp)

式中，τc为流致底剪切应力；τw为浪致底剪切应力；φcw为浪和流之间的夹角，详情见附录1.1。

Van Rijn[17]的底剪切应力模型计算时间平均的有效浪-流合致底剪切应力为

3.3.2 不同粒级颗粒临界起动剪切应力的参数化计算

考虑颗粒间黏性作用、底质体积浓度变化的影响，得到改进的临界起动剪切应力（τcr）计算方程[34]，

式中，cgel为底质沉积物的胶凝体积浓度；cgel,s为纯砂质沉积物最大体积浓度；Dsand取值62.5 μm；D表示颗粒粒径；γ为经验系数（取1.5）；τcr,o为非黏性颗粒临界起动剪切应力（附录 1.3）；ρcs为黏土组分（粒径小于 8 μm）含量百分比。

除了黏性作用的影响，不同颗粒之间还会因隐藏-暴露效应而相互影响。为了表征这种效应，Egiazaroff[35]提出了一个校正系数ξi（i为组分编号），计算方程为

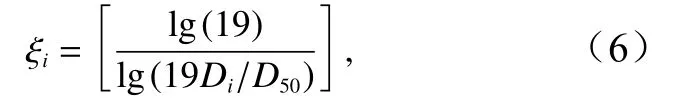
式中，D50为底质的中值粒径。

Kleinhans和Van Rijn[36]提出计算方程

式中，P为经验系数，通常介于0～-1之间，本文取原文中推荐的均值-0.65。

校正后的临界起动剪切应力(τcr,Di,corr)为

3.4 悬浮物浓度剖面分布的参数化计算

平衡状态下的SSC的垂向分布总是表现为从底层到表层逐渐降低的趋势，这一垂向分布形态取决于悬浮物沉降速度、底剪切应力和理查森数[19]。假定悬浮颗粒的沉降与向上的扩散达到平衡即处于稳定状态，再悬浮浓度剖面可以由对流扩散方程的自由表面边界条件表示[37]，

式中，C(z)为距底z处的SSC；Ca,i为组分i的参考浓度（附录2.1），当底剪切应力小于组分i的临界启动剪切应力（τcr,Di）时，Ca,i=0；za为参考浓度对应的高度；ws,i为组分i的沉降速度，本文ws,i的最小值取1 mm/s（附录2.2），εs,i(z)为组分i在距底z处的扩散系数（附录2.3）。在不同的假设条件下，式（9）有不同的解。

（1）当假设εs,i(z)随着距底高度增加呈抛物线形态变化、ws,i为定值时，式（9）有解析解，即经典的Rouse 分布剖面：c/c={[(h-z)/z][a/(h-a)]}ws/κu*，c为距a底z处的SSC，ca为参考浓度，h为水深，a表示参考浓度的距底高度，u*为总摩阻流速，κ为Von Karmen常数，取0.4。（2）当假设ε(z)满足 Van Rijn[17,19]s,i提出的考虑沉积物浓度分层效应的计算方法（附录2.3）时，式（9）没有解析解，可以采用基于积分定义的方法求解。

悬浮物的来源主要包括两种形式：局地再悬浮和平流输运。式（9）的计算结果只能反映再悬浮时刻观测站位的SSC剖面分布，要得到与观测数据相近的结果，还需考虑平流输运的影响。

本文假定观测站位周围区域在同一时刻有着相同的SSC，则随着时间的推移SSC剖面呈现出近似于局地再悬浮浓度剖面逐渐沉降的形态，即

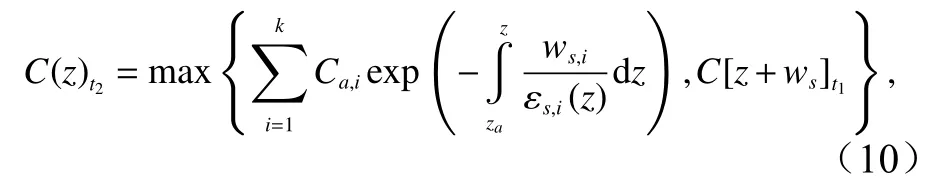
式中，t2=t1+1，C(z)t2表示t2时刻距底z处的SSC；C[z+ws]t1表示t1时刻距底[z+ws]处的SSC。基于这一假定，求得时间序列的再悬浮浓度剖面。此外，再悬浮浓度剖面以同水深观测浓度的最小值作为背景浓度，从而得到最终的模拟SSC剖面。

3.5 物质输运的计算

3.5.1 推移质输运的参数化计算

Van Rijn[38]提出了分粒级计算推移质输运的公式，

式中，q b为推移质输运速率；ρs为沉积物的密度；ρ为海水的密度（缺省值1 027 kg/m3）；pi为底质中组分i占比；fi=Dsand/Di且大于等于1；为组分i的无量纲粒径，g为重力加速度（缺省值9.8 m/s2），s=ρs/ρ，v为水的运动黏度（缺省值 1.36×10-6m2/s）；为浪-流合致底剪切应力；为超过临界值的剪切应力。

3.5.2 水平方向悬浮物单宽通量的计算

SSF（单位：g/(m·s)）) 计算公式为

式中，h为水深；u和v分别为流速的东向和北向分量；SSFu(v)分别为SSF的东向和北向分量；t表示时间（单位：h），当t=1时，计算结果为瞬时通量，当t=25时，计算结果为周期平均的瞬时净通量。由调和分析可知，研究区最主要分潮是M2和K1，因此时间平均的净通量计算近似选取2倍的M2分潮周期，即25个小时为1个周期。

因为观测数据缺乏底层的流速分布，所以需要参数化方法求解。在海床底面以上数米的范围内，流速(u(z))与高度(z)之间满足对数分布，

公式(14)的应用范围在浅水(水深数米)约为底面以上数厘米，在陆架海区 (水深数十米)约为流致底边界层厚度的20%～30%[8]。流致底边界层的厚度为δU，δU=0.44u*/f，f为科氏参数[39]。经计算，在约99.6%的观测时间里，流致底边界层的厚度大于等于5 m；在约83.5%的观测时间里，底边界层流速对数层的厚度大于等于5 m。所以本文将5 m定义为研究站位底边界层厚度，并用公式(14)计算其流速剖面。

4 参数化方案的对比

4.1 剪切应力分析

4.1.1 底剪切应力计算模型对比

如图3a所示，在两个观测站位，τc-Soulsby(Soulsby模型计算值)和(Van Rijn模型计算值)是基本一致的，但τw-Soulsby要略大于图 3b中，τm-Soulsby、τmax-Soulsby 和在趋势上一致，两者更加接近，差异主要是浪致底剪切应力差异造成的。因为本文的后续计算使用了Van Rijn提出的诸多经验公式，所以剪切应力使用Van Rijn模型的计算结果。

4.1.2 临界起动剪切应力计算方法对比

图4给出了T01站不同方法计算的τcr，在粒径小于32 μm颗粒内使用校正系数ξ1(公式(6)) 计算的τcr明显大于其他3种方法，所以公式(6)在计算粒径小于32 μm颗粒的τcr时可能偏大。本文使用的是公式(5)的计算结果，即计算过程考虑了颗粒间的黏性作用。

4.2 不同对流扩散方程假设的对比

为了选取最优的再悬浮浓度剖面参数化方案，本文挑选了不同假设条件下两个站位若干再悬浮时刻的对流扩散方程计算结果进行对比(图5)。当综合考虑浓度分层效应和底质粒级多样性时，模型结果与ADCP反演的SSC对应最好。以中值粒径代表底质计算得到的浓度剖面显著小于分粒级计算的浓度剖面，其主要原因是中值粒径的起动剪切应力高于较细粒的颗粒，导致计算的总参考浓度相对较小，该现象说明在黏性颗粒占一定比例的海区，中值粒径并不能完全代表底质进行再悬浮浓度剖面的计算。此外，忽略分层效应会导致计算的浓度剖面在上下层几乎一致，即随距底高度的增加SSC变化不大。因此为了更准确地表达再悬浮浓度剖面，本文后续计算使用了考虑浓度分层效应和底质粒级多样性的方法。

5 结果与讨论

依据月相、风速（图6）和水位（图7a，图7e）数据，将观测数据分为3个阶段（图6）。S1: 1～142时为大潮阶段；S2: 143～198时为大风阶段（风速大于10.8 m/s定义为大风天气）；S3: 199时到观测结束为小潮（伴随短时大风）阶段。

5.1 风和水动力环境

观测期间，研究海区风速的平均值是7.9 m/s，最大风速16.9 m/s。S1期间，风向主要是在西北到东北之间摆动，S2期间主要为西北风，S3期间风向在西到北之间摆动（图6）。

图3 Soulsby[8]和Van Rijn[17]模型计算底剪切应力的对比Fig.3 Comparison of bed shear stress calculated by Van Rijn's[17] and Soulsby's[8] models

图4 T01站8种粒径组分不同临界启动剪切应力(τcr)计算方法的结果对比Fig.4 Comparison of the results of different critical bed-shear stress (τcr) calculations for 8 particle size fractions at T01 Station

观测流速反映了研究海区具有混合半日潮的特征（图6），最大流速对应着涨潮、落潮的中间时刻（图7a,图7e）。T01站的潮流方向为西北-东南向，距底5 m最大流速（0.64 m/s）出现在S2期间。在S2期间，T01站东向流明显增强，西向减弱（图6）。T02站主要表现为规律的近东-西向的潮流，距底5 m最大流速 （0.76 m/s）出现在S1期间。T02的最大流速从S1到S3有明显的减弱, S2期间并没有出现类似于T01同时段的流速极大值。

图5 T01和T02站在不同时刻的再悬浮浓度剖面与观测浓度剖面的对比Fig.5 Comparison between modeled SSC profile and measured SSC profile at observation stations T01 and T02 at different time

T01站最大有效波高为3.44 m，最大波周期为7.5 s，S2期间平均有效波高为2.26 m，平均波周期为6.54 s（图7b）。T02站最大有效波高为2.88 m，最大波周期为9.5 s（第137、138时），S2期间平均有效波高为1.98 m，平均波周期6.85 s（图7f）。因为波浪的能量随着水深增加而逐渐降低，所以T01站底层的波浪轨道流速（Uw）大于T02站。波浪轨道流速的趋势由有效波高（Hs）和波周期（T）共同决定，且均为正相关关系。当水深h＜0.1gT2或h＜10Hs时，波浪才会产生明显作用于底质的震荡流速[8]。依据这一标准，T01站波浪作用的平均水深约为42 m，T02站波浪作用的平均水深约为46 m，所以T01站底质再悬浮受到潮流和波浪（有效波高及波周期）的共同影响，T02站底质再悬浮主要受潮流的影响。

图6 观测站位T01和T02的风速和距底5 m的流速Fig.6 Wind speed and current velocity at 5 MAB at observation stations T01 and T02

5.2 剪切应力和悬浮物浓度

T01站位的浪-流合致底剪切应力范围为0.003～0.429 N/m2（图 7c）），在 S2 期间和 S3 的部分时刻浪致底剪切应力贡献明显，最大浪-流合致底剪切应力和最大浪致底剪切应力对应着同一时刻。T02站位的浪-流合致底剪切应力范围为0.001～0.365 N/m2（图7g），大风期间浪致底剪切应力贡献小，最大合致底剪切应力和最大流致底剪切应力对应着同一时刻。

T01站的3个阶段均有显著的底质再悬浮，再悬浮时刻（τcw＞τcr）占观测时间的比例均超过 26%（图 7c），最大值出现在S2期间达到58%。在S2期间受波浪作用的影响，再悬浮作用加强，T01站观测SSC（以ADCP反演的距底5 m SSC为例）也有明显的升高（图7d）。T02站3个阶段再悬浮时段占观测时间的比例依次递减，S3期间再悬浮时段占比只有6%。T02站在S1期间再悬浮作用较强（图7g），平均观测SSC明显大于S2和S3（图7h），而在S2期间SSC没有明显升高。

总体来看，观测SSC对底质再悬浮有很好的响应，尤其是在T01站的S1、S2和T02站的S1期间（图 7c, 图 7d, 图 7g, 图 7h），说明在这些时间段内观测站位底边界层SSC剖面分布主要受再悬浮控制。

5.3 模拟与观测悬浮物浓度对比

T01站位距底5 m模拟SSC与观测SSC的对比表明，在第115～124小时期间，T01站观测SSC出现了持续约9个小时的高值，而模拟SSC高值仅与底剪切应力高值对应，只出现在第115个小时前后（图7d）。这一现象可能是因为该时段SSC空间分布不均，渤海一侧的高浓度水体向东输运到观测点形成持续的SSC高值[5,12]。观测SSC较模拟SSC有滞后现象，在距底5 m的位置大约滞后2个小时。第175个小时前后模拟峰值明显高于观测峰值，其可能原因是在经历一次大风事件后，再悬浮颗粒还未沉降，底质沉积物供应不足，所以实际浓度达不到理论值。第252个小时前后，模拟SSC突然出现了高值，这是因为该时刻同时具备较大的扩散系数（εs）和底剪切应力（图7c）。因为模拟过程使用的观测波浪周期是间隔1 h的瞬时值，存在一定的偶然性。而该时刻波周期对应着一个低谷（图7b），导致扩散系数计算值较大，造成了模拟与观测SSC不一致的峰值。T02站观测SSC与模拟SSC在S1期间对应最好，观测SSC较模拟SSC同样有1～2 h的滞后（图7h）。

通过两个站位模拟与观测SSC的对比发现，该计算模型更加适合潮流控制的海区，当有明显波浪作用时，模拟结果比单纯考虑潮流作用时差，主要表现为观测SSC的相对滞后以及观测波浪参数瞬时值的变化导致的扩散系数异常。

5.4 物质输运的讨论

5.4.1 参数化计算底边界层悬浮物通量的重要性

图7 T01和T02站位时间序列的数据Fig.7 Time series data of T01 and T02 stations

在T01站S1、S2和T02站S1的部分再悬浮时刻，参数化方案计算的底边界层内的水平方向悬浮物单宽通量（SSF_1h1）占全水深 SSF（SSFh）的比例 （SSF_1h1/SSFh）都显著高于底边界层内水通量相对全水深水通量的比例（T01站约为 13%，T02站约为10%）（图 8）。T01站再悬浮时刻SSF_1h1/SSFh的平均值约21%，最高值约49%；T02站再悬浮时刻SSF_1h1/SSFh的平均值约17%，最高值约47%。这表明在再悬浮时刻，底边界层SSC的垂向变化对SSF有不可忽略的影响。

为了进一步量化SSC的垂向变化对底边界层SSF计算结果的贡献，本文对比了参数化计算底边界层SSC与用定值代替底边界层SSC这两种情况下，底边界层SSF计算结果的差异。在T01站S1、S2和T02站S2的部分再悬浮时刻，SSF_1h1显著高于将SSC 视为定值计算的底边界层 SSF（SSF_2h1）（图 8）。其中，T02站S1期间SSF_1h1/SSF_2h1的值比T01站S2期间相对更高，这主要是受扩散系数的影响。扩散系数表征沉积物扩散的难易，扩散系数越大，沉积物越容易发生扩散。受到波浪混合作用的影响，T01站位S2、S3期间颗粒扩散系数超过T02站S1期间1倍以上（图7c, 图7g），再悬浮物更加容易扩散到上层水体，SSC在垂向上分布更加均匀，导致SSF_1h1/SSF_2h1相对减小，即波浪作用导致S2期间再悬浮时刻的SSF_1h1/SSF_2h1小于 S1。

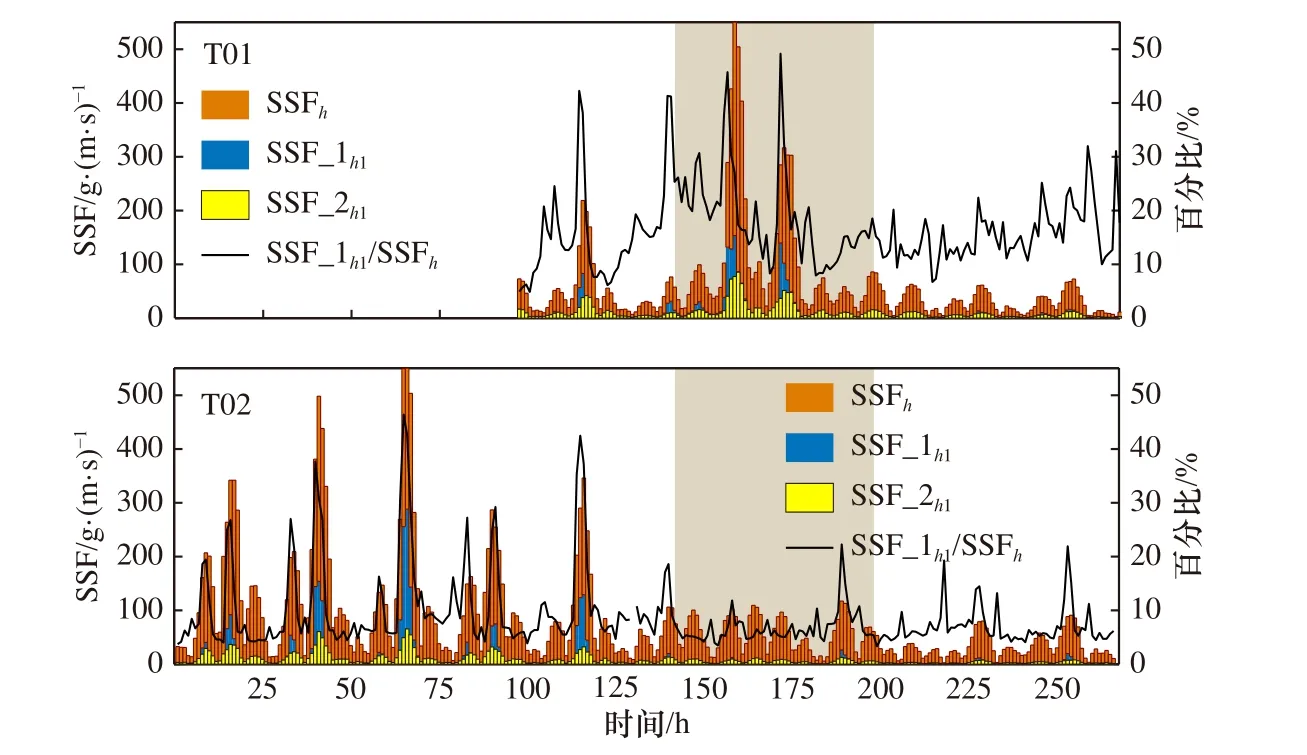
图8 比较参数化计算底边界层（BBL）SSC与用定值代替底边界层SSC这两种情况下，底边界层时间序列SSF计算结果的差异Fig.8 The differences of the calculation results of time-series SSF in BBL under the comparison between SSC calculated by parameterization scheme and SSC in BBL replaced by the constant

前人在计算SSF时总是忽略底边界层SSC的垂向变化[5,7]，为了从定量角度比较差异，本文分别用SSF_1h1和SSF_2h1计算了全水深周期平均的SSF并计算相对误差P(P=(SSF_1h1-SSF_2h1)/(SSF_2h1+SSFh-SSF_1h1)·100%)。计算结果为两个站位S1期间的平均相对误差P≈44%，S2期间平均相对误差P≈10%，S3期间平均相对误差P≈0%。参考前人的统计结果，研究海区冬季的平均大风天气数约为51 d[40]。假设大风天气发生在大潮或小潮期间的概率相当，则依据本文参数化方案估算的渤海海峡冬季平均SSF比传统方法计算结果高约16%。

5.4.2 悬浮物通量和推移质输运量

两个观测站位在观测期间总体的SSF趋势是“北进南出”，即T02站悬浮物由北黄海向渤海输运，T01站悬浮物由渤海向北黄海输运（表3）。T01站只有在S2期间的沉积物输运方向为由西向东，S1、S3期间均为由东向西，但是S2期间平均SSF是其他两个阶段的4～12倍，这表明西北大风对渤海海峡南侧沉积物向北黄海输运有重要贡献。

基于前人的研究结果，在底质粒径小于300 μm的条件下，悬浮物输运量远大于推移质输运量（＜1%）[34]。本文在观测期间计算的推移质通量普遍比SSF低两个数量级左右，与前人结果相近。这表明，推移质输运在渤海海峡沉积物输运量研究中可以忽略（表3）。

表3 T01和T02站平均悬浮物通量（SSF）和推移质通量分析对比Table 3 The comparison of mean SSF throughout the whole water column and bed-load transport

6 结论

依据渤海海峡冬季的定点连续观测资料，本文描述了研究站位大潮、小潮和大风阶段的水动力特征，并用实测数据说明了西北大风对渤海海峡冬季物质输运“北进南出”格局的重要影响。

为了探讨底边界层沉积物输运的重要性，本文利用简化的一维参数化方案，计算了研究站位底边界层的SSF和推移质输运量。为了验证不同参数化方法的可靠性，计算过程对比了不同的参数化方法：（1）Soulsby和Van Rijn提出的两种计算底剪切应力模型的计算结果相近；（2）不同临界起动剪切应力计算方法的差异较大，临界起动剪切应力的计算需考虑颗粒间黏性作用的影响；（3）垂向一维对流扩散方程模型的不同解法与实测数据对比结果表明该模型可以用来定量计算研究区再悬浮时刻SSC，计算过程中要考虑沉积物浓度的分层效应和底质不同粒级颗粒临界起动剪切应力的差异；具体来说，不考虑浓度分层效应会导致SSC在水体上下层几乎一致，而以中值粒径代表底质的粒径分级计算得到的剖面SSC相对偏小。

沉积物输运的研究结果表明，在有显著再悬浮作用的时段，底边界层SSC是垂向变化的。受SSC垂向梯度的影响，渤海海峡冬季底层5 m的SSF占全水深SSF的比例（T01站约为21%，T02站约为17%）显著高于相应层位水通量占全水深水通量的比例。经估算，如果不考虑SSC在底边界层的垂向变化，水平悬浮物通量的平均相对误差在大风期间约为10%，大潮期间约为44%。依据本文参数化方案估算的渤海海峡冬季平均的SSF比传统方法计算结果高约16%。此外，渤海海峡冬季推移质比悬移质输运低两个数量级左右，在研究沉积物输运通量时可以忽略。

致谢：本研究海上观测工作搭载了“东方红2”号科考船执行的黄、渤海共享航次。感谢中国海洋大学海洋地球科学学院王保铎老师和诸位同门在现场观测和室内实验中提供的支持与帮助。