基于Chirp数据和Biot-Stoll模型反演南海北部陆坡海底表层沉积物物理性质

周庆杰，李西双，刘乐军，刘洋廷，高珊，周航，王景强，李天光

(1.自然资源部第一海洋研究所 海洋沉积与环境地质国家海洋局重点实验室，山东 青岛 266061；2.青岛海洋科学与技术试点国家实验室 海洋地质过程与环境功能实验室，山东 青岛 266061；3.青岛海洋科学与技术试点国家实验室 海洋矿产资源评价与探测技术功能实验室，山东 青岛 266071)

1 引言

海底浅表层（海床之下小于1 m范围内）沉积物位于海底海水与沉积地层交界处，主要由砂、粉砂、黏土和孔隙流体（海水）等物质组成，承载了大量且丰富的沉积环境信息[1]。近年来，利用Biot-Stoll模型和浅剖声呐数据反演海底表层沉积物物理性质的研究正在成为一个新兴的浅剖数据应用方向。Schock[2-3]利用Biot-Stoll模型和Chirp声呐数据反演了美国东部Fort Walton海滩和南海海底沉积物的声速、密度、孔隙度等物性参数，且与实验室测量值吻合度较高。国内也有学者应用Biot-Stoll模型和原位测量数据探讨声波在海底沉积物介质中的传播规律[4-7]，并将该模型用于反演沉积物粒径、孔隙度、密度等物性参数[8-9]。然而，Biot-Stoll模型在不同的海域采用不同的参数所预测的声学性质和物理性质之间的关系存在差异，因此，针对特定的海域利用实测物理参数构建Biot-Stoll模型，才能获得较为准确的声学和物理参数预测关系。

浅地层剖面是利用声学方法了解地下介质的物理信息，海底反射系数与沉积物的物理性质密切相关。在常规地震资料反演中发展了许多计算反射系数的理论和方法，如随机稀疏脉冲反褶积[10]、谱反演[11]、稀疏地层反演或基追踪反演[12]、谱稀疏贝叶斯学习反射系数反演[13]等反射系数反演方法。本文在借鉴常规海底反射系数反演方法的基础上，利用地震反褶积技术对浅剖数据进行处理求取其海底反射系数，为反演海底表层沉积物物理性质提供有效的数据支撑。

南海北部陆坡区地形复杂，发育了一系列陆坡峡谷地貌[14]，其沉积物沉积速率较高具有复杂的分层结构[15]，从而影响了沉积物物理性质和声学反射特性的分布特征。本文以研究区海底表层沉积物的声速、密度、孔隙度等实测资料为基础，利用Biot-Stoll模型计算海底表层沉积物的法向入射反射系数，并与样品实测数据得到的反射系数进行对比，分析模型预测海底反射系数的可靠性，并建立海底反射系数与沉积物物理性质之间的相关关系。在研究区选取典型的Chirp剖面计算其海底反射系数，结合基于Biot-Stoll模型建立的海底反射系数与沉积物物理性质之间的相关关系反演表层沉积物的孔隙度、密度、平均粒径等物理性质，并与取样点处实测物理性质结果进行对比，探讨该方法的适用性，为快速获取连续的海底沉积物物理性质提供新的方法参考。

2 Biot-Stoll模型及参数简介

Biot模型作为一种经典的多孔弹性理论模型[16-17]，同时考虑介质的孔隙性与弹性，在描述各向异性和具有黏弹性的双相饱和多孔介质中应用广泛。Stoll[18]在Biot模型基础上提出了Biot-Stoll模型，应用于海底沉积物介质中的声速和声衰减计算，并推导出了简谐平面波在多孔介质中传播的方程，

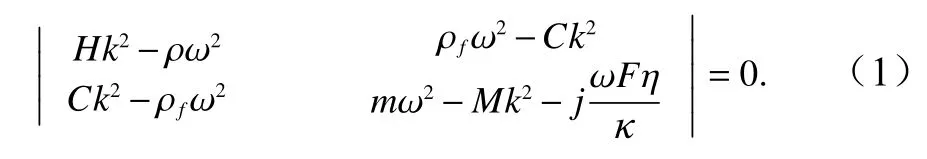
式中，ρ为体密度；ρf为孔隙流体密度；ω=2πf为角频率；参数为宏观压力梯度下流体流动的相位（其中，c为曲折度，n为孔隙度）；j为虚数；Fη是用于解释泥沙孔隙中振荡流的频率依赖性黏性损失的一种黏性修正因子；k为复波数。此外，Biot理论弹性模量H、附加弹性模量C和复弹性模量M可表示为

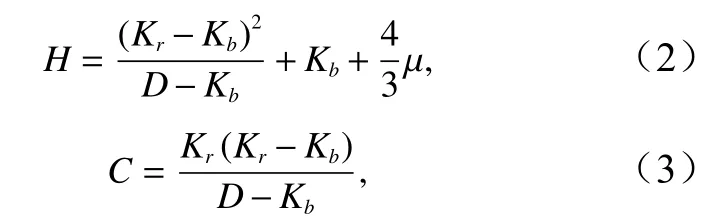
式中，Kb为骨架体积模量；μ为骨架剪切模量；Kr为颗粒体积模量；Kf为孔隙流体体积模量；n为孔隙度；复波数可表示为虚数（v为声波相速度，α为声波衰减）。

在海底表层沉积物与海水的分界面假定孔隙流体沿与界面垂直的方向连续进出骨架，界面总应力平衡且界面流体压力平衡，在这些边界条件的限定下，可以确定海床的反射系数R[2]（图1），

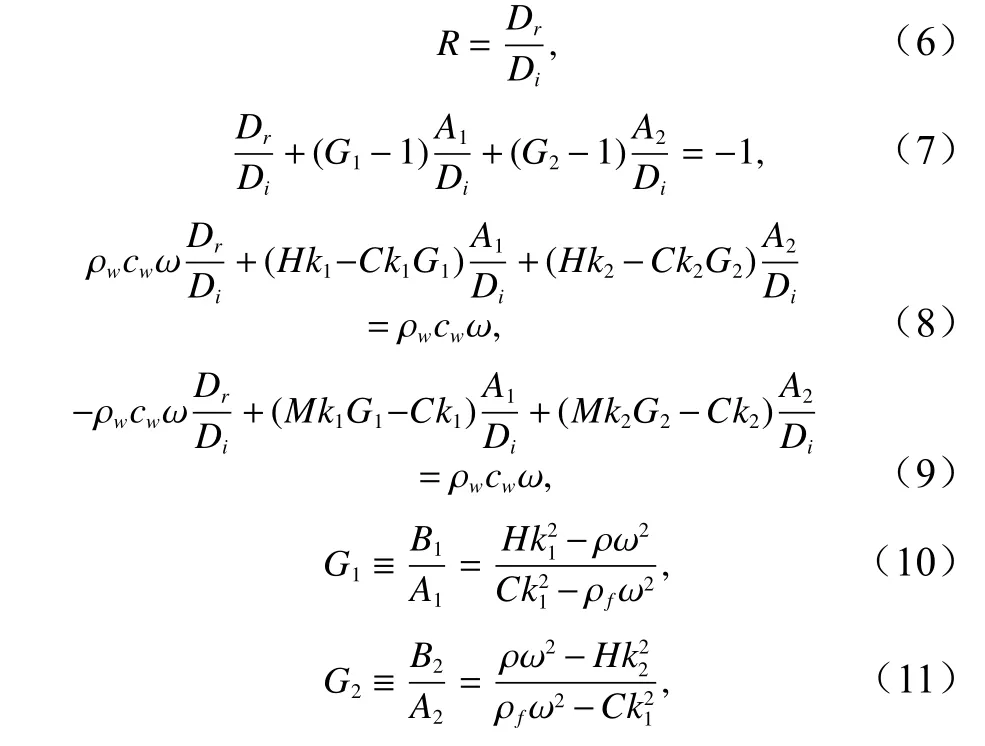
式中，A1和A2分别为沉积物骨架在快波和慢波作用下的复位移振幅值；B1和B2分别为快波和慢波作用下孔隙流体相对于骨架运动的复相对位移；Di和Dr分别为入射波和反射波的复位移振幅值； ρw和cw为海水的密度和声速；k1和k2为快慢纵波的波数，其他字母含义同公式（1）。

3 试验测量与理论计算

3.1 区域概况及数据获取

研究区域位于南海北部陆坡区，发育多条海底峡谷，地形地貌复杂[19-20]，水深 400～2 500 m（图 2）。南海北部陆坡区海底表层沉积物存在两种成因类型[21]，一是来源于河流搬运的现代细粒碎屑物质，二是早期晚更新世冰期低海平面的残留沉积。受物源区沉积物自身特征及后期改造作用的影响，沉积物颗粒组分呈现出粗粒与细粒交错沉积的特征，含量较多的粗粒物质主要是高能环境中长期沉积的产物，在冰后期海平面上升的过程中，可能被细颗粒沉积物覆盖[22]。在南海北部陆坡区海底沉积物存在明显的分带性分布特征[23]，浅水区沉积物以粉砂质黏土、粉砂质砂为主，水深大于1 000 m的深水区域沉积物主要为细颗粒的黏土质粉砂和粉砂质黏土[24-25]。南海北部陆坡区水深变化较大且沉积速率较高[26-27]，浊流及块体搬运作用强烈[28-29]，其沉积物孔隙度变化范围较大，沉积物声学物理性质分布的差异性变化明显[30]。

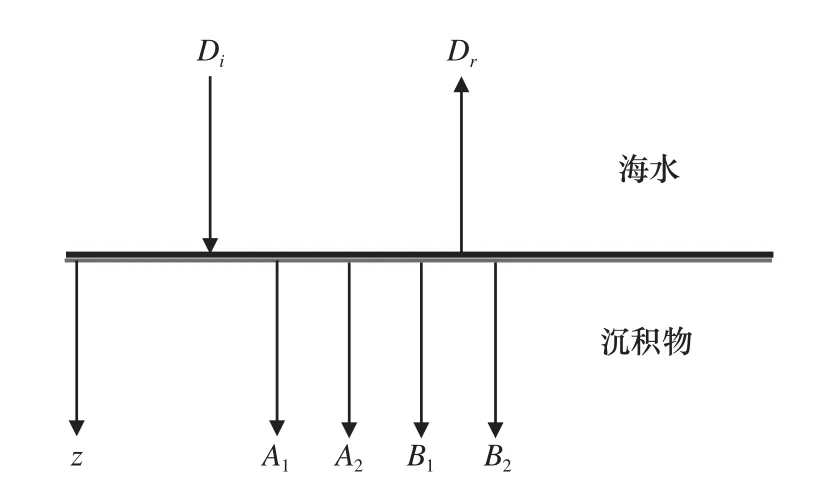
图1 Biot参数计算反射系数的几何示意图（据文献[2]）Fig.1 Geometric sketch of reflection coefficient calculated by Biot parameter (according to reference [2])

图2显示了研究区、取样站位及典型Chirp浅剖测线的分布位置。沉积物柱状样由“海洋石油708”船于2015年2月采用深水重力柱取样器进行采样，每根样品长6 m。样品取回后在实验室内进行了含水量分析、粒度分析、土粒比重测试等试验分析，获得了样品的含水量、粒径、湿密度、孔隙度、颗粒密度等参数。同时，以0.5 m为间距，采用WSD-3数字声波仪和同轴差距法进行了声学测量，测量频率为25 kHz，其中样品长度测量精度为0.05 cm，声时测量精度为±0.1 μs。浅地层剖面数据是利用船载ECHO SOUNDER3500浅地层剖面仪获得，主频3.5 kHz。

3.2 Biot-Stoll模型输入参数

由于Biot理论模型涉及的参数较多，参数的选取对计算结果有不同程度的影响。陈静等[6]曾选取不同模型参数对Biot-Stoll模型在南海南部海底沉积物物理性质预测的准确性方面进行了研究，认为Schock参数与实测结果更为接近。本文模型输入的颗粒密度、孔隙度、湿密度、粒径等参数为实测数据，其他参数，如渗透率、沉积物孔隙因子、颗粒体积模量和剪切模量、孔隙水体积模量等参数，以及海水密度和弹性模量等参数的变化对模型计算结果影响较小，这些参数的选取，结合Schock参数公式[2]确定或从文献资料中获取，详细参数取值如表1所示。

3.3 海底反射系数的求取

由于海水与海底沉积物介质性质（波阻抗）差异较大，声波在海底界面会发生强反射，海底反射系数Rs可表示为

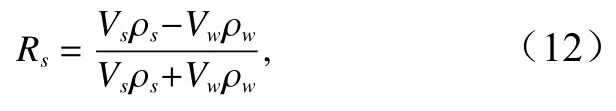
式中，Vs，ρs为海底表层沉积物的声速和密度；Vw，ρw为海水的声速和密度。基于海底表层沉积物样品的声学测量和物理性质测试可以获得沉积物声速和密度值，结合研究区海水的声速和密度经验值[23,30]，根据上述公式可以计算获得取样点处附近的海底反射系数。

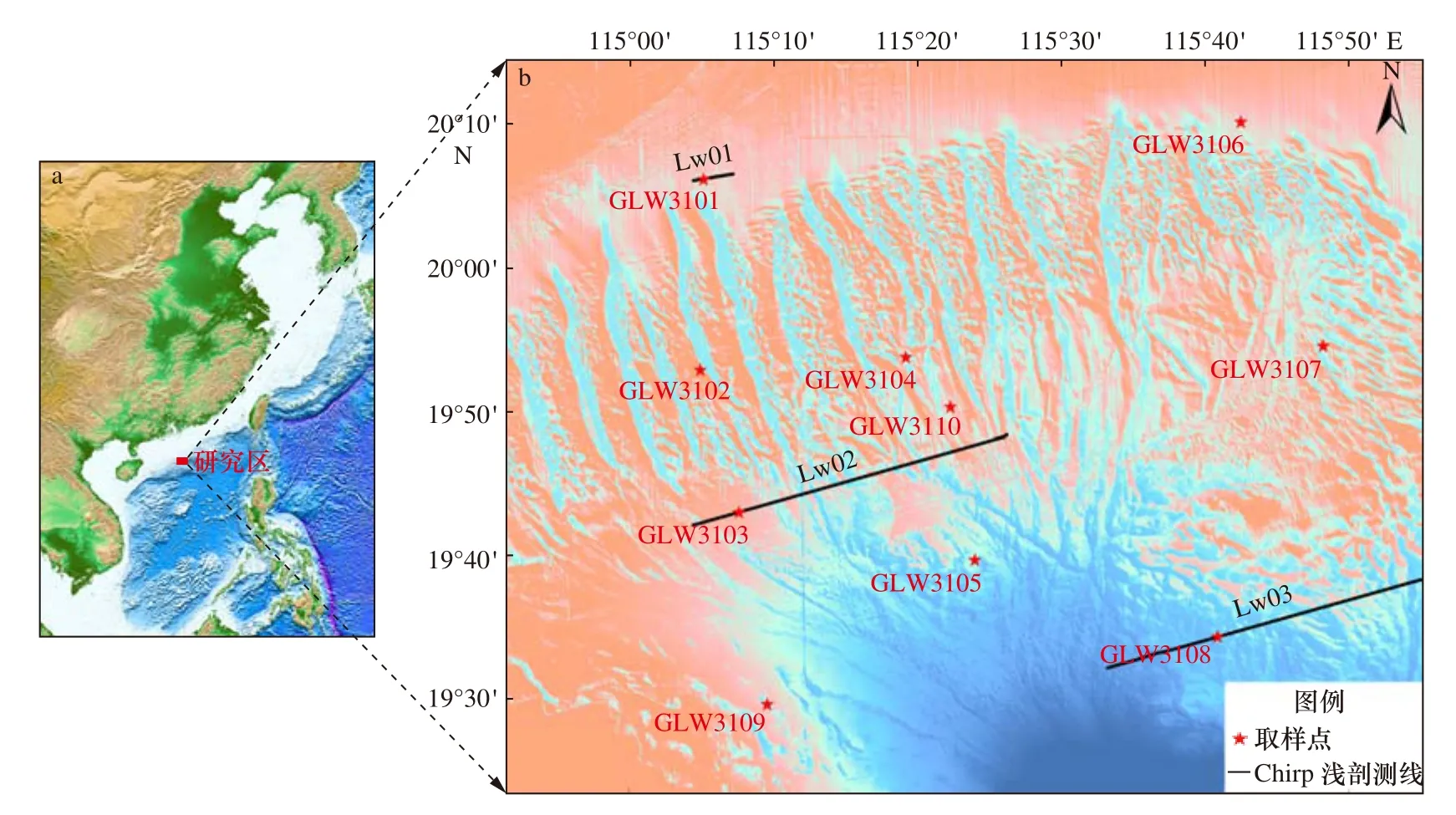
图2 研究区位置、表层沉积物取样站位及典型Chirp浅剖测线分布Fig.2 The location of the study area, surface sediment sampling stations and typical Chirp shallow profiles

表1 Biot-Stoll模型输入的沉积物物理参数Table 1 The input sediment physical parameters of the Biot-Stoll model

在浅地层剖面上，海底地震记录可以简单的认为是震源子波与海底反射系数相褶积的结果，可以利用地震反褶积技术进行子波处理消除子波的影响，得到实际反射系数序列[31]。在海底反射系数求取之前，需要结合浅地层剖面记录中的海底反射波及其对应的双程旅行时和相关的海水声速测量结果，进行波前球面扩散补偿，以提高浅剖资料的保真度。在海水中波前发散对反射波振幅的衰减因子为

式中，D为衰减因子；v0为初始速度；vR为各海水层均方根速度；t为地震波双程传播时间。补偿因子为

球面扩散能量损失是传播路程中球面波前半径的函数，用球面扩散补偿因子对地震道加权就补偿了球面扩散作用对地震振幅的衰减损失。由于球面扩散补偿是一种三维补偿，从理论上来讲具有较高的保幅性[32-33]。

在计算海底反射系数过程中，根据Chirp浅剖的频带特征（表2）定义子波[34]，给出初始海底反射系数并与子波进行褶积，然后计算褶积结果与原始记录的误差，根据误差判断收敛条件，若收敛则结束计算，输出海底反射系数，否则继续迭代计算。图3为计算海底反射系数过程中的子波及合成记录与原始剖面的对比。图4为以Lw01剖面为例计算得到的海底反射系数剖面，图中散点为计算得到的海底反射系数，红色实线为海底反射系数的平均值。

表2 Chirp子波相关参数Table 2 The relevant parameters of Chirp wavelet

4 结果与讨论

4.1 反射系数实测值与模型预测值比较

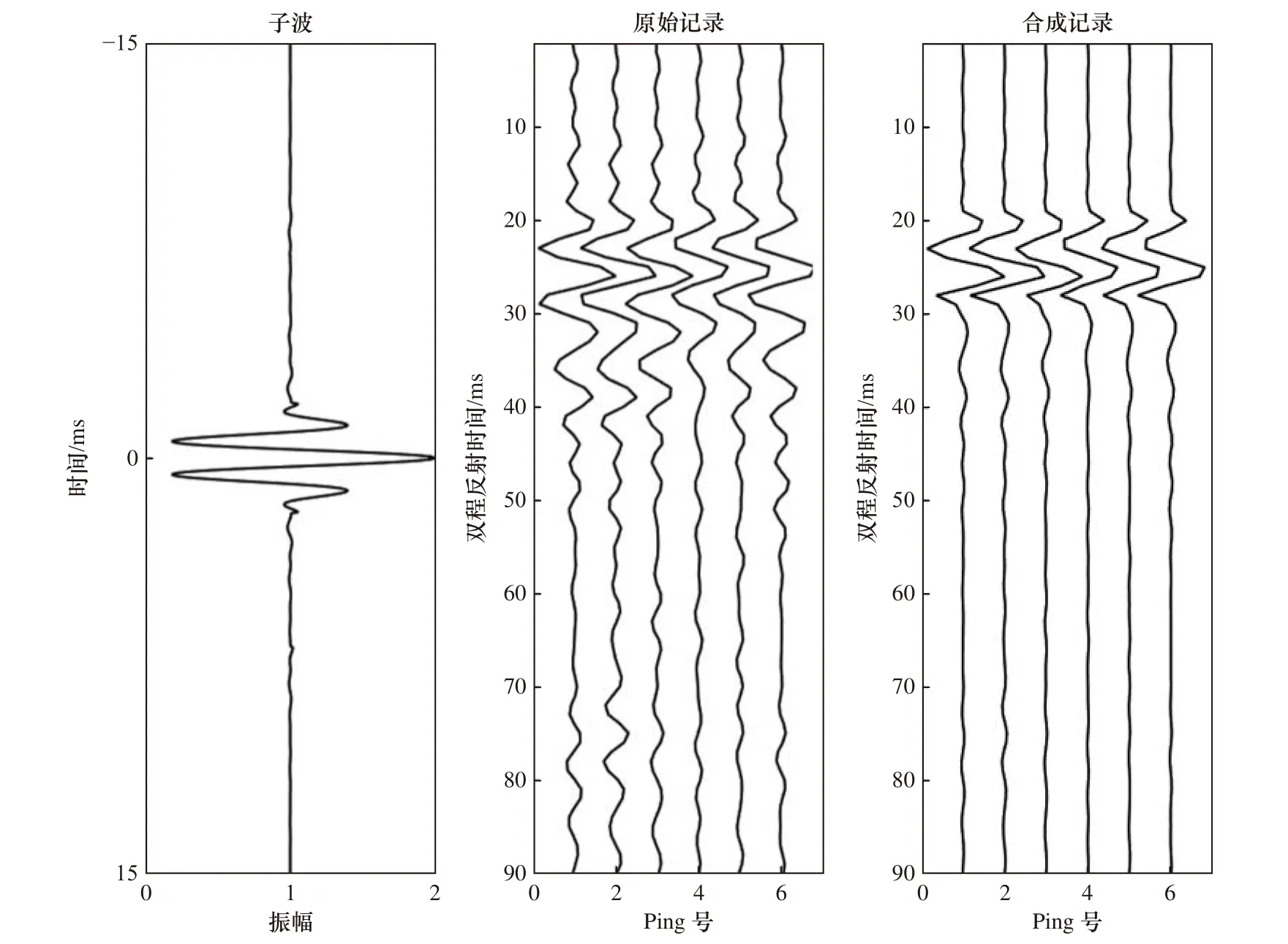
图3 子波褶积合成记录与原始剖面数据对比Fig.3 The wavelet convolution synthetic seismogram and original section data

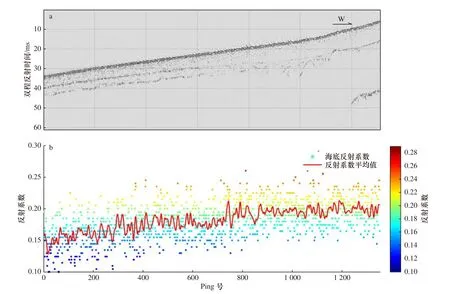
图4 Lw01剖面计算得到的海底反射系数Fig.4 Sea bottom reflection coefficients calculated from Profile Lw01

为比较反射系数模型预测值与实测值，分析反射系数预测模型的适用性，利用Biot-Stoll模型进行了海底反射系数计算，计算所采用的参数见表1。图5显示了反射系数随孔隙度的变化关系，可以看出，Biot-Stoll模型计算的反射系数变化曲线与实测海底反射系数平均值基本吻合。对Biot-Stoll模型的反射系数预测值与实测值进行差值计算，孔隙度小于0.8范围内，模型预测值与实测值的偏差在0.1%～3.8%之间，平均偏差为1.2%，孔隙度大于0.8时偏差较大，约为4.9%。由表层沉积物取样测试结果来看，该区沉积物孔隙度大部分都小于0.8，因此，在该区利用Biot-Stoll模型进行计算是可行的。

4.2 基于Biot-Stoll模型建立的海底反射系数与物理性质关系

基于Biot-Stoll模型研究了海底反射系数随频率的变化关系，计算了频率3.5 kHz时（Chirp浅剖主频3.5 kHz）海底反射系数与沉积物孔隙度、密度、平均粒径之间的相关关系，建立拟合方程（图6）。由图6a可以看出在低频（f＜103Hz）时，海底反射系数受频率变化的影响较小，在高频（f＞103Hz）时，海底反射系数随频率的增大而减小，且随孔隙度的增大这种趋势逐渐减小；图6b为海底反射系数与沉积物孔隙度的变化关系，随孔隙度的减小反射系数呈增大的趋势；图6c为海底反射系数与沉积物密度的变化关系，可以看出其近似呈线性关系，为提高拟合的准确度，本文以二次方程对其进行拟合；图6d为海底反射系数与沉积物平均粒径的变化关系，可以看出，反射系数与平均粒径呈负相关，随平均粒径的增大而减小。

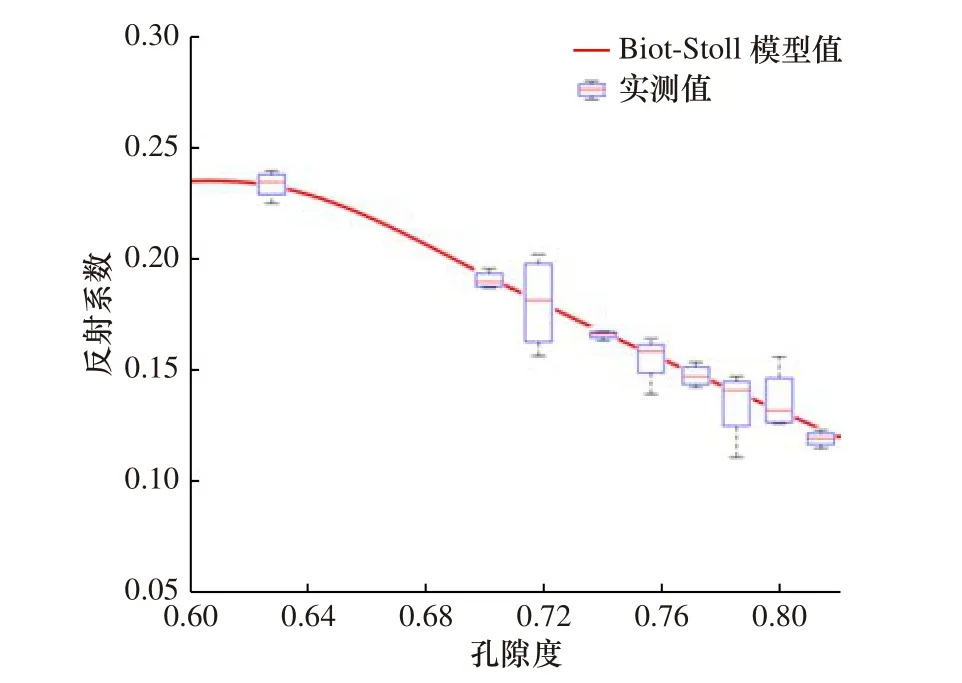
图5 反射系数与孔隙度的关系Fig.5 The relationship between reflection coefficient and porosity

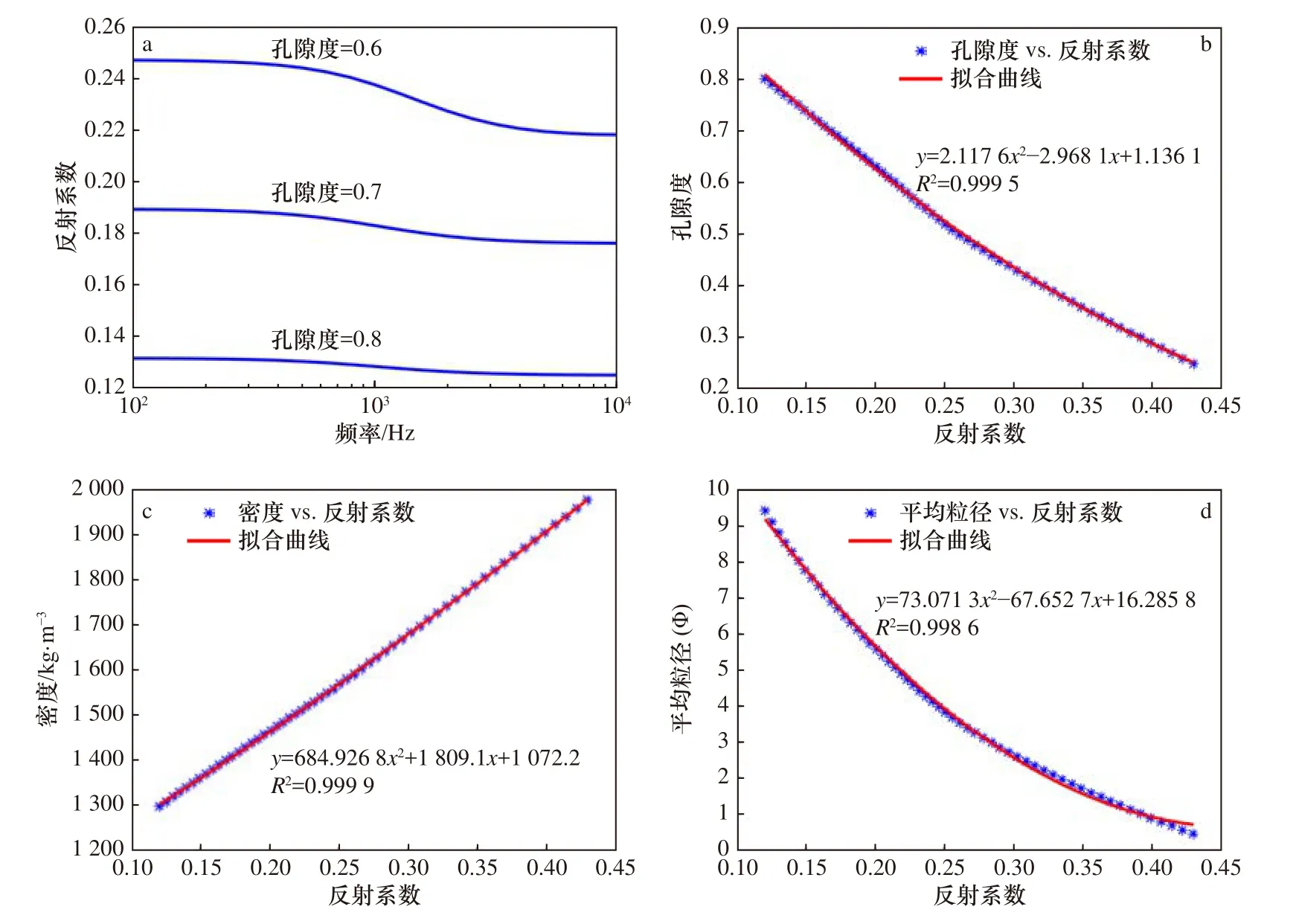
图6 海底反射系数与沉积物物理性质的相关关系Fig.6 Correlation between bottom reflection coefficients and sediment physical properties

4.3 物理性质反演结果与实测结果对比

在研究区选取典型的Chirp浅地层剖面计算其海底反射系数（其中较为典型的3条剖面，位置见图2b），利用基于Biot-Stoll模型所建立的海底反射系数与沉积物物理性质之间的相关关系，对海底表层沉积物物理性质进行反演，得到这些剖面的海底表层沉积物孔隙度、密度和平均粒径等物理性质，对于这3个物理参数的反演，在反演任何一个物理参数的过程中，其他两个物理参数也会发生对应的变化（图7），其中孔隙度与平均粒径变化趋势相近，与密度变化趋势相反。由图可见，这3条剖面的海底反射系数整体位于0.09～0.25区间范围内，最高约为0.25；Lw01剖面的反射系数较Lw02和Lw03剖面变化幅度较小，这是由于Lw01剖面位于海底峡谷上部，地形起伏较小，地势相对平坦，水动力条件较弱，沉积物以黏土为主含少量粉砂[35]；Lw02和Lw03剖面分别位于海底峡谷中部和下部，地形起伏较大，尤其是Lw02剖面横切海底峡谷，地形变化最大（图8），水动力环境较强，浊流及块体搬运作用发育，沉积物中含水量（孔隙度）变化较大[29]，相应的海底反射系数变化幅度增大，说明海底地形的变化在对沉积物的物理性质形成一定影响的同时，形成海底反射系数的差异性变化；Lw03剖面位于海底峡谷区尾部，水深相对较深，沉积物主要以黏土为主，孔隙水含量（孔隙度）较高。从反演的物理性质结果来看，孔隙度的分布范围在0.52～0.85之间，大部分集中在0.6～0.8区间范围内；密度分布主要集中在1 300～1 500 kg/m3区间范围内，平均约为1 420 kg/m3；平均粒径在4Φ～10.5Φ区间范围内，最高约为10.5Φ，最低约为4.1Φ，平均约为7.3Φ。

利用Lw01Lw02Lw03剖面所经过的GLW3101GLW3103GLW3108站位的样品实测孔隙度、密度、平均粒径与反演的结果进行对比（表3）。可以看出，取样站位处反演的孔隙度、密度、平均粒径与实测结果相对误差0.31%，最大为4.60%，均小于5.0%；此外，海底表层沉积物取样测试结果显示，水深大的区域，沉积物孔隙度较大，Chirp剖面反演结果与实测值整体相符，说明基于Biot-Stoll模型在该区建立的海底表层沉积物反射系数和物理性质之间的相关关系是可靠的。

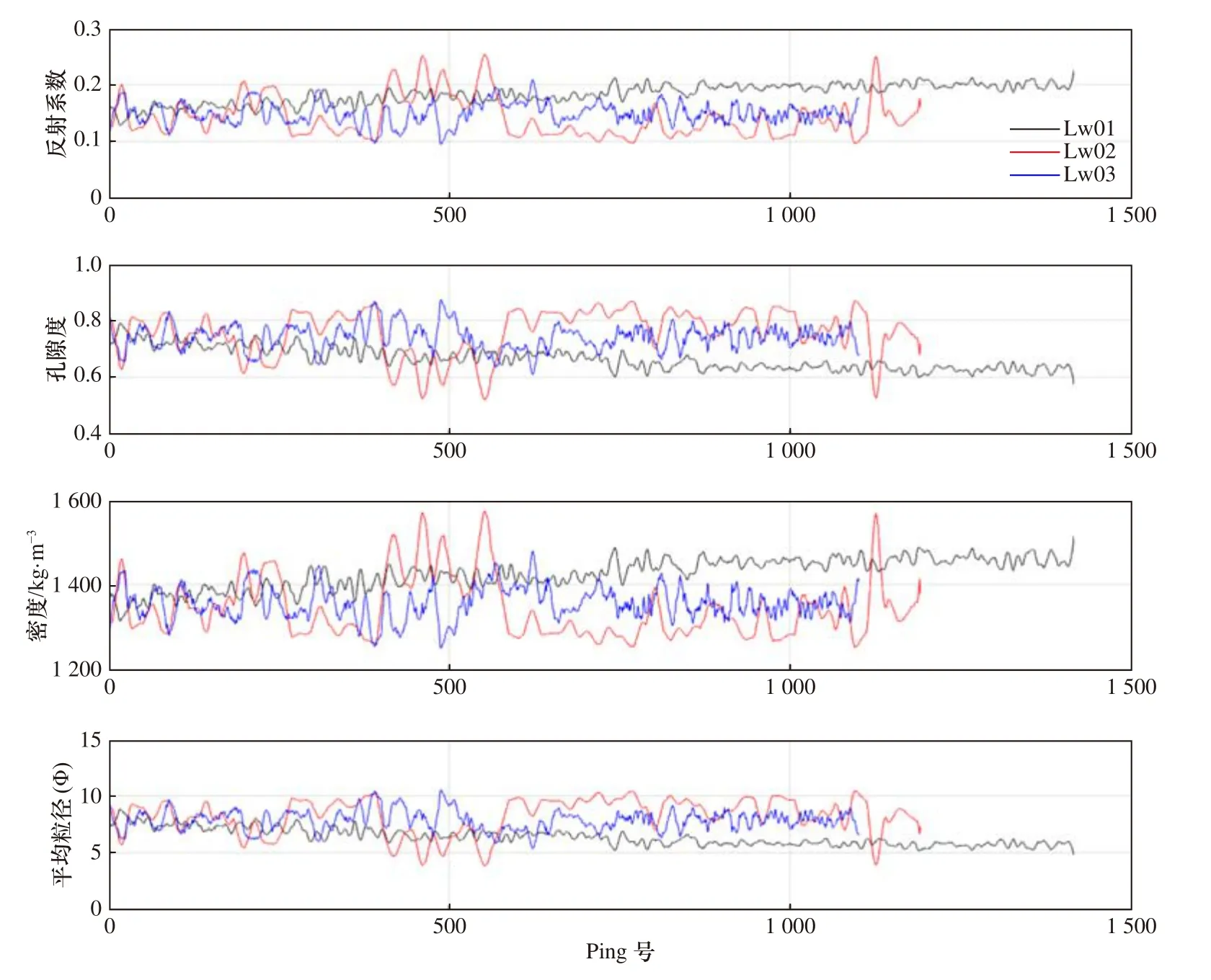
图7 Lw01、Lw02、Lw03剖面沉积物物理性质反演结果Fig.7 Inversion results of sediments physical properties in profiles Lw01, Lw02 and Lw03

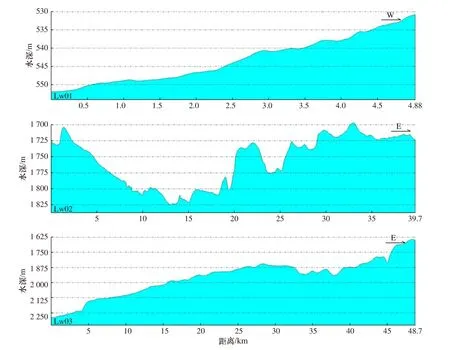
图8 Lw01、Lw02和Lw03测线对应的海底地形剖面图Fig.8 The seabed topography section of profiles Lw01、Lw02 and Lw03

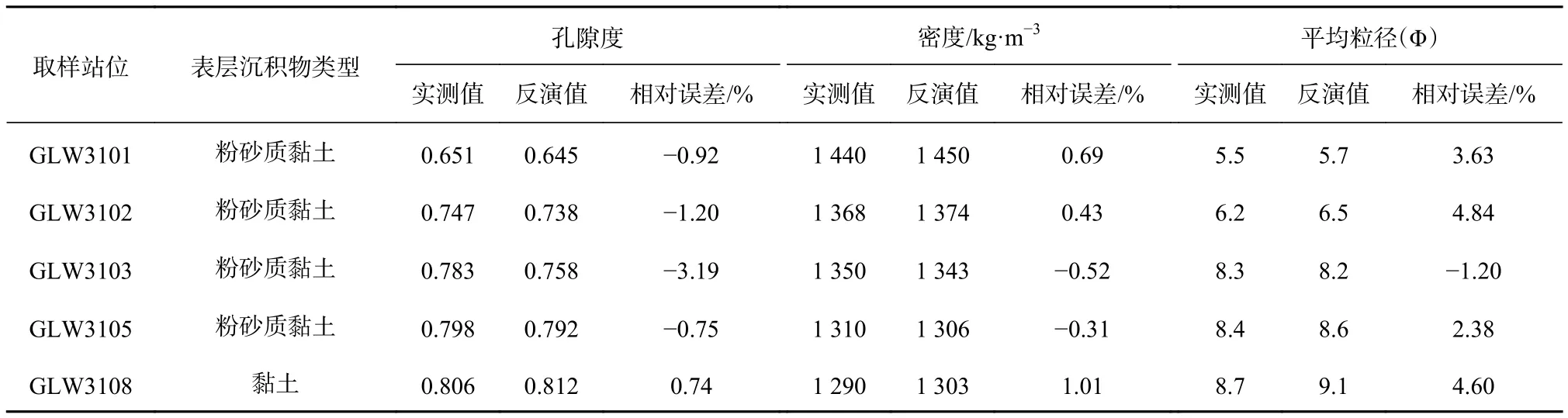
表3 站位实测物理性质与反演结果对比Table 3 Comparison between the measured physical properties and the inversion results

5 结论

通过对南海北部陆坡表层沉积物样品测试和Biot-Stoll模型计算，分析了模型预测海底反射系数的可靠性，并选取典型的Chirp剖面计算其海底反射系数，反演表层沉积物的孔隙度、密度、平均粒径等物理性质，得到以下认识：

（1）实测海底反射系数与Biot-Stoll模型计算值的对比分析表明，模型计算值与实测值的吻合度总体较好。在孔隙度小于0.8时，模型计算值与实测值的平均偏差约为1.2%，孔隙度大于0.8时偏差增大，约为4.9%。且研究区表层沉积物取样测试结果显示绝大部分区域沉积物孔隙度在0.8以内，因此，在该区利用Biot-Stoll模型进行计算是可行的。

（2）在利用Biot-Stoll模型研究海底反射系数随频率变化关系的基础上，建立了频率3.5 kHz时海底反射系数与沉积物孔隙度、密度、平均粒径之间的关系方程，且方程拟合度较高，可决系数R2均大于0.99，为利用海底反射系数反演沉积物物理性质提供了可靠的转换依据。

（3）选取典型Chirp剖面进行计算其海底反射系数并反演了海底表层沉积物孔隙度、密度、平均粒径等物理性质。反演结果与实测结果对比分析表明，反演结果误差在0.31%～4.84%，均小于5.0%，表明该反演方法在南海北部陆坡区的应用是可行的，可为在该海域间接快速获取海底沉积物物理性质提供新的方法参考。