近50年来乌江水沙特征变化研究
郭文献,李 越,查胡飞,王鸿翔
(华北水利水电大学,河南 郑州 450045)
乌江是长江上游南岸的最大支流,也是我国十三大水电能源基地之一[1-2],对流域内的经济发展做出重要贡献;随着人类活动频繁加剧,特别是水利工程的修建,在一定程度上引起乌江水沙特性发生改变。水利工程的拦截作用改变了下游河流自然流动状态,这势必会对流域内水沙和生态造成一定影响。近几十年来,国内同时出现大量的科学文献以研究人类活动对河流水沙状况的影响[3-7]。鉴于以往单独对乌江控制水文站武隆站研究较少,且有关研究采用的方法较为传统且单一,不能系统阐述其水沙特征变化规律。本文通过乌江流域武隆站实测径流泥沙数据资料,采用Mann-Kendall非参数检验法,均值差异T检验,双累积曲线法和小波分析等方法对乌江水沙特征及影响因素进行研究,以便更好的了解人类活动对乌江流域水沙特性的影响。
1 研究方法
1.1 研究区域及数据
研究区域为乌江流域,流域集水面积87 920 km2,干流全长1 037 km,天然落差2 124 m,为长江上游右岸的最大一级支流,流域内多年平均径流量为4.82×1010m3,多年平均输沙量为1.92×107t。其中,武隆水文站位于乌江下游,为乌江汇入长江的控制水文站;故研究采用武隆水文站1956年~2015年的径流量、输沙量数据资料分析近几十年来乌江径流泥沙演变过程及其影响因素。其中的径流泥沙数据来源于长江流域水文年鉴。
1.2 Mann-Kendall非参数检验法
Mann-Kendall非参数检验通过计算时间序列数据的标准化变量UF,与某一置信水平α(取0.05)下的临界变量对比。当UF为正表示有上升趋势,为负则表示有下降趋势;当UF超出临界值时表明上升或下降趋势显著。同时对原时间序列的逆序列进行同样的统计量计算,使UB=-UF,若两条曲线在95%置信度水平内出现交点,表明在该时间点发生突变,方法具体计算参考文献[7- 8]。
1.3 均值差异T检验法
Mann-Kendall非参数检验不受样本值和分布类型的干扰,但是检验过程中可能出现多个突变点,需要对这些突变点进行验证。均值差T检验法假定时间序列某一时段的平均值与另一时段平均值之间差异具有充分的统计显著性,则认为在给定信度范围内的选定时间点上出现了突变现象[9]。即,可以针对某一基准点进行突变性检验。具体步骤如下。
定义样本长度为N的序列突变指数为
AI=|X1P-X2P|/(S1+S2)
(1)
式中,X1p和S1为基准年前M1年的平均值和标准差;X2p和S2为后M2年的平均值和标准差。计算时采用连续移动基准年的方法,就可得突变指数AI的时间序列。
定义统计量
t=(X1p-X2P)/[Sp(1/M1+1/M2)1/2]
(2)
(3)
式中,M1和M2为基准年前后两段序列的样本长度;SP为联合样本方差。统计量t服从自由度为M1+M2-2的t分布。当给出一定的显著水平α,如t 小波分析的基本思想是一簇小波函数系来表示或逼近某一信号或函数。在小波变换中,比较常用的小波函数有Mexican Hat小波、Dmey小波和Morlet小波等[12]。本研究选取复Morlet小波对乌江流域水沙时间序列进行周期性分析。复Morlet小波函数是小波分析的关键,小波分析是指具有震荡性、能够迅速衰减到零的一类函数,亦即小波函数φ(t)∈L2(R)且满足 (4) 式中,φ(t)为基小波函数,可通过尺度的伸缩和时间轴上的评议构成一簇函数系 (5) 式中,φa,b(t)为子小波,若φa,b(t)是由式(5)给出的子小波,对于给定的能量有限信号f(t)∈L2(R),其连续小波函数为 (6) 双累积曲线是检验两个参数间关系一致性及变化的方法,通过在直角坐标系中绘制同时期内一个变量连续累积值与另一个变量的连续累积值关系曲线,可用于水文气象要素一致性检验、缺值插补及趋势性变化和强度分析[14-15]。 为揭示乌江流域多年径流泥沙变化趋势,采用武隆站径流泥沙多年统计资料点绘出武隆站1956年~2015年的年径流量和年输沙量相关图(见图1)。 图1 武隆站年径流量和输沙量变化 从图1可以看出,在研究区间内除1966年、1981年和2006年(1966年和2006年为枯水年,1980年乌江渡水电站正式蓄水)年径流量出现较大波动外,年径流量整体上无明显变化。年输沙量和年径流量在20世纪70年代中期之前保持较好的一致性,基本呈现大水大沙、小水小沙的状态;中期后输沙量开始呈下降趋势,到2000年后基本已不足1×107t,下降趋势极为明显。 由于武隆站径流量和输沙量年际变化波动性较强,直观地观察其变化规律存在一定局限;为定量评估年径流量和年输沙量变化趋势,采用Mann-Kendall非参数检验进行趋势性变化评价。经计算,年径流量、输沙量的Mann-Kendall标准化变量UF分别为-0.50,-7.14。取显著性水平α=0.05,则对应的临界值UFα=1.96;而|UF|径流量<|UF|α,|UF|输沙量>|UF|α。因此,乌江流域近50年来年径流量无明显下降趋势,而年输沙量下降趋势显著,通过95%置信度检验。 根据Mann-Kendall统计检验结果分析(见图2),武隆站多年径流量基本处于0.05显著水平范围内,年径流量UF和UB曲线交点出现在2010年且交点均落入0.05显著性水平内,表明径流量突变点可能发生在2010年。输沙量在1958年~1975年呈增加趋势,1975年后开始呈减少状态,1980年后超出95%置信度检验,且下降趋势不断增强;年输沙量UF和UB曲线相交于1992年,但交点并未落入0.05显著性水平范围内,但考虑到20世纪80年代末乌江流域内已建电站1 630座[16],总库容达到44.06亿m3,水库拦沙效果显著,因此也将1992年考虑为可能突变年份。 图2 武隆站径流量、输沙量Mann-Kendall统计值 为了检验Mann-Kendall非参数检验法对武隆站突变结果的准确性,采用均值差异T检验对上述突变结果进行验证。选取显著性水平α为0.01,其对应的临界值tα为2.704,计算结果参见表1。对于年径流量,当M=55时,突变指数为0.35,对应的统计量1.59 表1 武隆站年径流量和输沙量均值差异T检验 从图3小波分析中可看出,径流量存在着明显的年际变化特征。在较大时间尺度上,20世纪80年代之前主要存在25~28 a的周期变化规律,经历了丰→枯→丰3次交替变化;20世纪80年代后变化为径流量为20~25 a的周期变化规律,经历了枯→丰→枯→丰4次交替并且两个阶段的周期变化表现都较为稳定。在小尺度周期上,主要存在13~15 a,8~11 a和3~5 a的周期性变化规律,且小尺度周期上丰枯变化较为频繁。由径流量小波方差图(见图3)可以看出,年径流变化的主周期为28、15、11 a和5 a,其中,以28 a未主周期的小波方差最大,说明乌江径流在28 a时间尺度上的周期性最为显著。 图3 武隆站径流量小波分析等值线图和小波方差 图4 武隆站输沙量小波分析等值线图和小波方差 从图4可以看出,在较大时间尺度上,20世纪70年代中期前主要存在20~25 a的周期变化规律,经历了丰→枯→丰3次交替变化,20世纪70年代中期后,周期变长且不连续,分析其原因与乌江流域梯级水电站开发导致输沙量显著下降有关,在小尺度周期上,主要存在8~10 a和3~6 a的周期性变化规律。从小波方差图中可以看出,输沙量变化以25、10、6 a为主周期。 双累积曲线法主要利用水沙累积的变化特点研究径流泥沙的变化,当双累积曲线为一条直线时,表明径流泥沙无明显变化;若累积曲线在某点发生明显转折,则表明水沙关系发生显著变化[17]。根据上述径流泥沙趋势性、突变性分析和武隆站径流量—输沙量双累计曲线(见图5),将大通站径流泥沙时间序列划分为1956年~1976年,1977年~1993年,1994年~2015年3个阶段。从图5中可以看出,3个阶段的线性拟合方程斜率表现为减小趋势,1974年~1993年线性拟合方程斜率减少相对平稳,而1994年~2015年线性拟合方程斜率明显降低,说明武隆站年输沙量在近20年来迅速减少。通过武隆站径流量—输沙量双累积曲线的线性拟合方程估算各阶段累积输沙量相对于上一阶段的减少量,具体计算方法参见文献[18]。分别将1993年和2015年武隆站累积径流值(184.31×1010m3和289.01×1010m3)分别带入公式y=0.741 3x-0.080 1和y=0.419 4x+26.878,可得1993年和2015年在曲线转折前的累积输沙量分别为136.54×107t和148.09×107t。将1993年和2015年武隆站的累积径流值分别带入y=0.419 4x+26.878和y=0.094 4x+88.241,可得1993年和2015年在曲线转折后的累积输沙量104.18×107t和115.52×107t。亦即,1977年~1996年和1997年~2015年两个阶段的累积减沙量分别为32.36×107t和32.57×107t。 图5 武隆站径流量—输沙量双累积曲线 图6 武隆站年径流量与输沙量关系 影响流域内径流量和输沙量的因素主要包括流域内下垫面条件、自然灾害、气候降雨、人类影响等[21],其中又以降雨和人类活动对河流产水产沙影响较大。乌江流域多年来年均降水量略有减少[22],且沿江取水稍有增加,但变幅不大,造成年径流量在一定程度上有所减少。这与上述Mann-Kendall分析中乌江年径流量无明显减少相一致;同时,各水文站Mann-Kendall趋势检验的水沙趋势性变化也不相同。这说明年径流量的减少对年输沙量显著减少造成一定影响外,人类活动对年输沙量减少也存在重要影响。人类活动主要包括水库蓄水拦沙、水土保持措施等综合因素,考虑到水土保持造成减沙量在200万~300万t[16],对乌江流域输沙量减少可忽略不计,因此本文重点考虑水库蓄水拦沙对乌江流域年输沙量的影响。 为了评价水库蓄水拦沙对乌江流域年输沙量的影响,以武隆站作为总控制站分析乌江流域内大型水库建设情况与武隆站输沙量年际变化的关系,绘出乌江流域的水库建设总库容与年输沙量变化关系曲线(见图7)。从图7中可看出,流域内水库建设总库容增加与年输沙量减少之间存在着良好的对应关系。截止到20世纪70年代中期,乌江流域建成一些水库,但由于库容相对较小,因此对武隆站输沙量减少造成的影响较小,输沙量在3.44×107t上下波动,无明显的下降趋势。截止到1979年乌江上第一座大型水电站乌江渡水电站建成蓄水后,水库拦截大量泥沙,造成武隆站年输沙量显著减少,年输沙量下降到1.88×107t左右,下降幅度达到45.35%。2000年后,随着洪家渡、构皮滩、思林等水电站陆续建成,水库的拦沙效应也不断增大,基本拦截河流泥沙,年输沙量下降到0.49×107t,武隆站年输沙量进一步减少。 图7 武隆站输沙量和累积库容变化过程 (1)通过径流泥沙的趋势性分析,武隆站径流量无明显变化,其Mann-Kendall标准化变量为-0.50,未通过95%置信度检验;输沙量的Mann-Kendall标准化变量为-7.14,通过95%置信度检验,表明输沙量下降趋势显著。 (2)根据Mann-Kendall非参数检验法和均值差异T检验法对武隆站径流泥沙进行突变分析,结果表明年径流量未发生突变,年输沙量在1992年发生突变,突变点对应的统计量t为8.32。 (3)通过小波分析可得,乌江流域武隆站径流泥沙序列存在多时间尺度变化特征,径流量和输沙量分别存在4类和3类时间尺度周期,年径流量变化以20~23 a为主要周期,年输沙量变化以25~28 a为主要周期。 (4)由径流泥沙的双累积和水沙关系阶段性分析将武隆站划分为1956年~1976年,1977年~1993年,1994年~2015年3个阶段。其中,1971年~1996年和1997年~2015年2个阶段的累积减沙量分别为32.36×107t和32.57×107t,且水沙关系、输沙能力在1974年~1993年变化最为明显。 (5)通过对乌江流域水库蓄水拦沙对年输沙量的影响分析可知,流域内水库建设总库容增加与年输沙量减少之间存在着良好的对应关系,随着累积库容不断增加,年输沙量逐渐减少,说明水库蓄水拦沙是导致输沙量显著减少的重要原因之一。1.4 小波分析

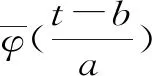
1.5 双累积曲线法
2 结果与讨论
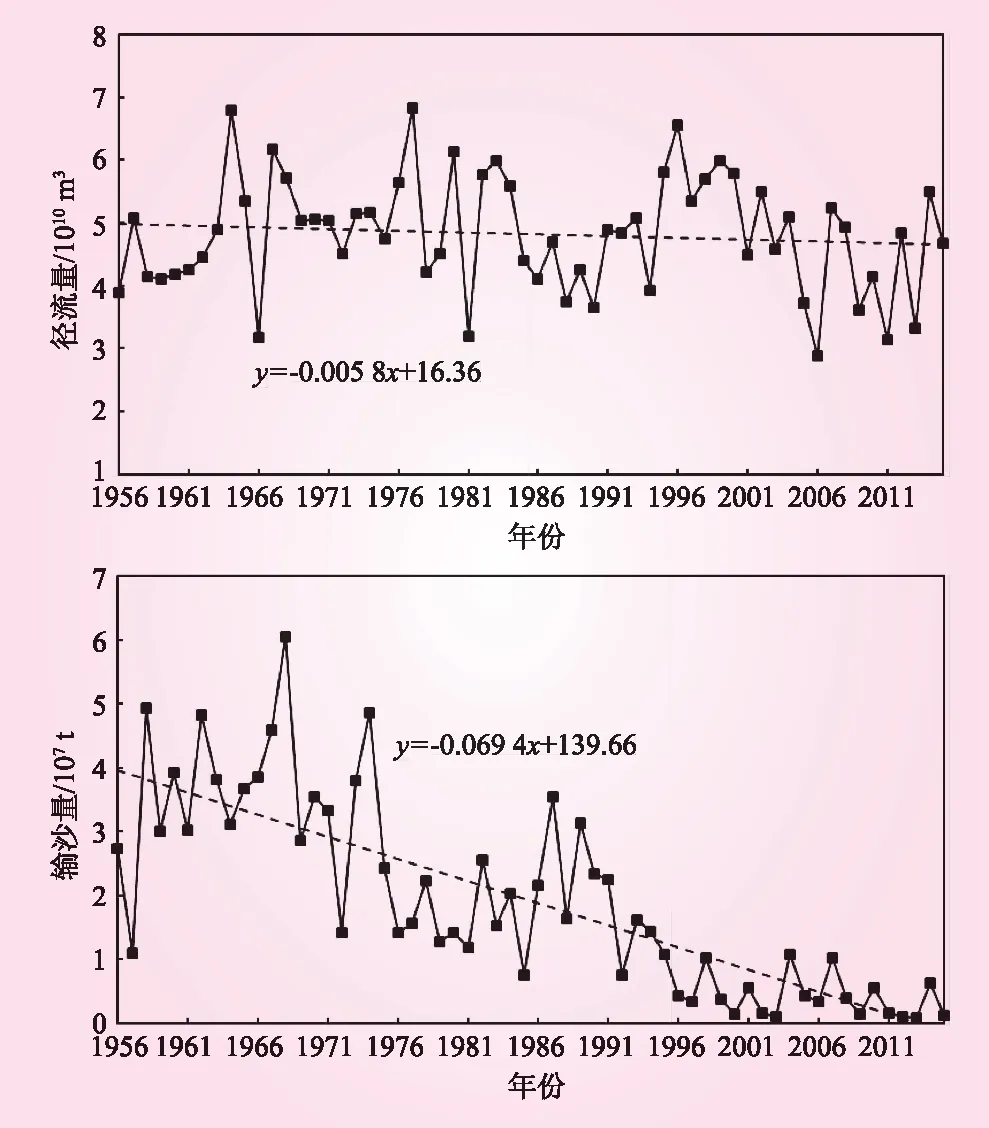
2.1 径流泥沙趋势性分析
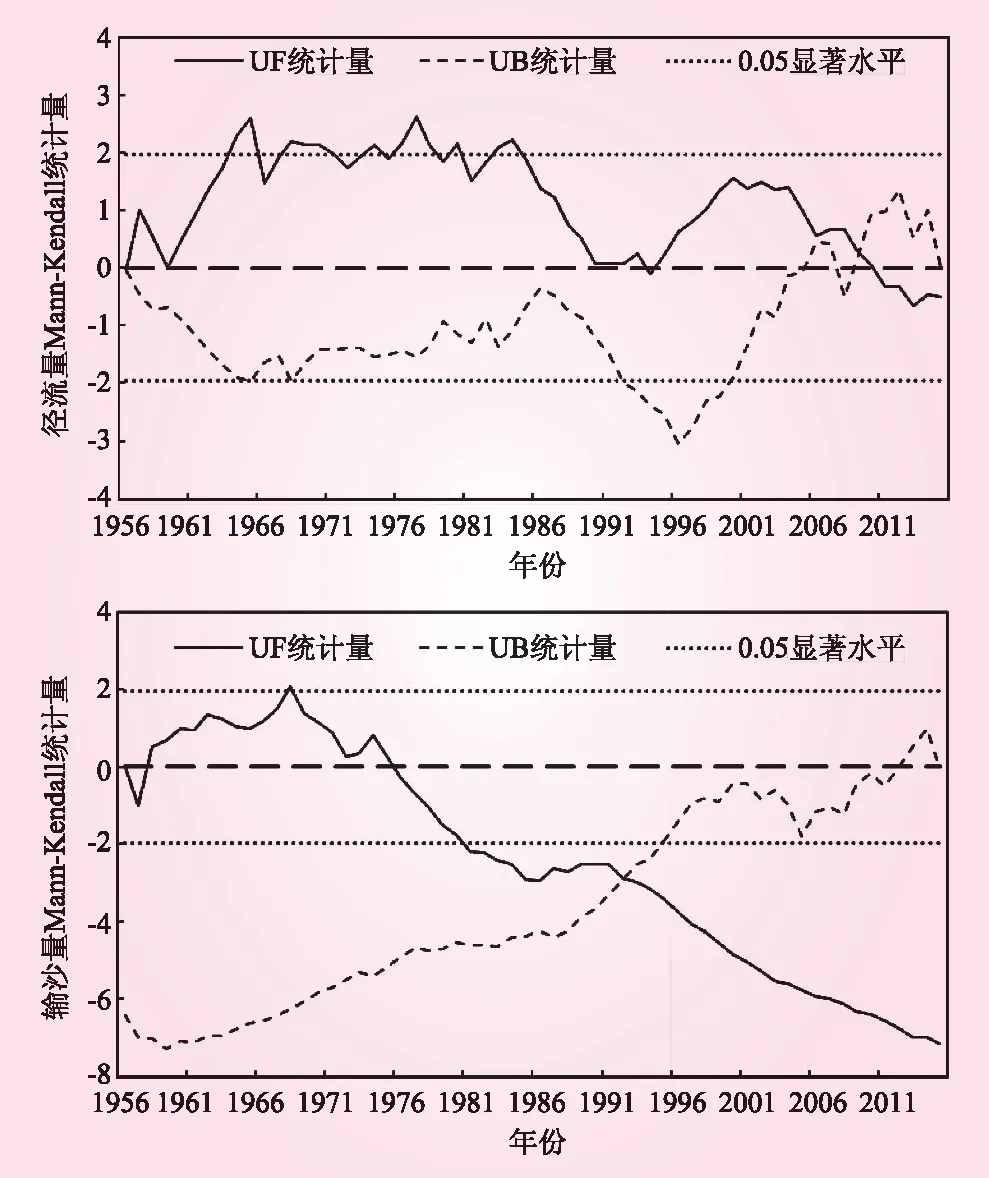
2.2 径流泥沙突变性分析

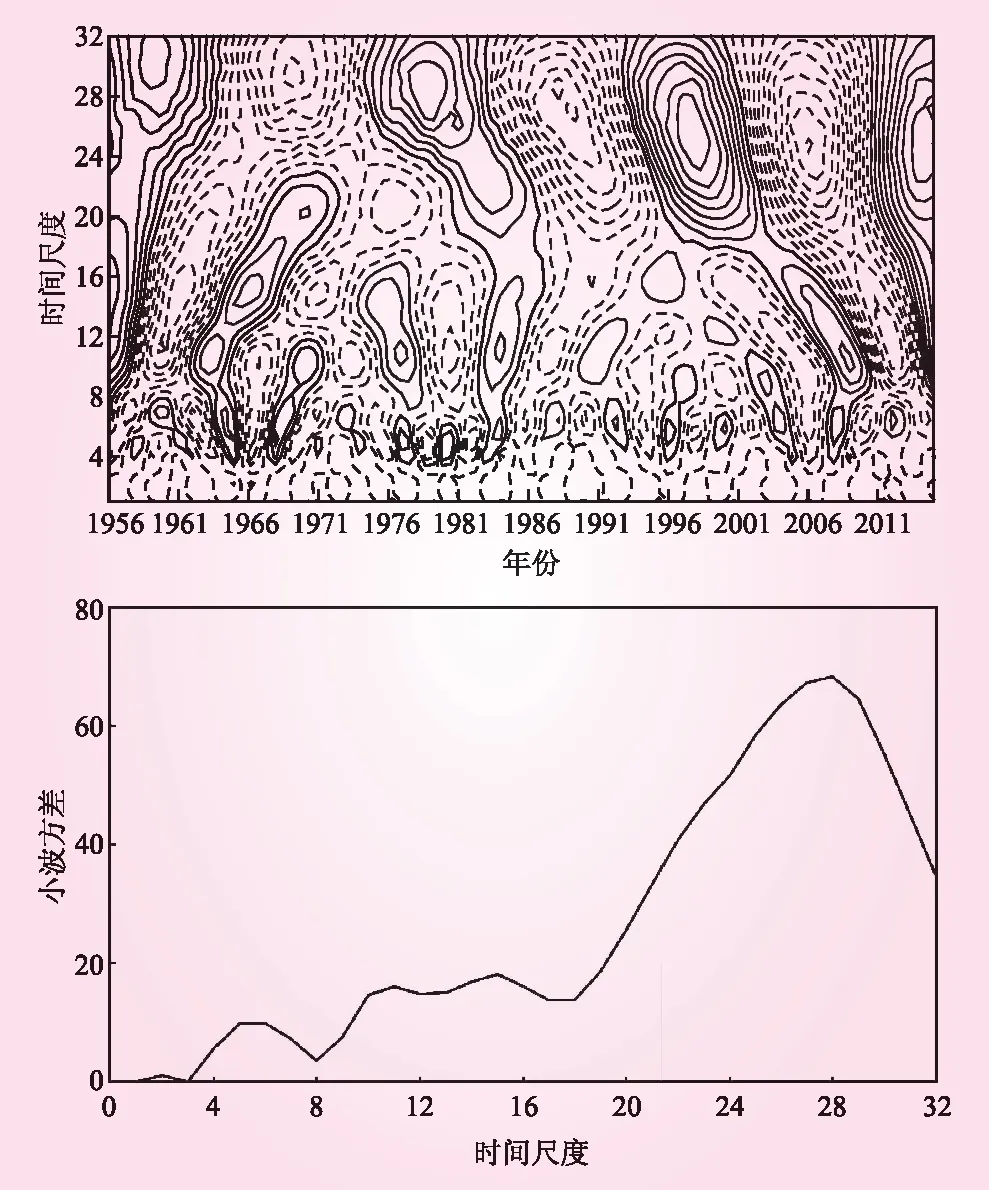
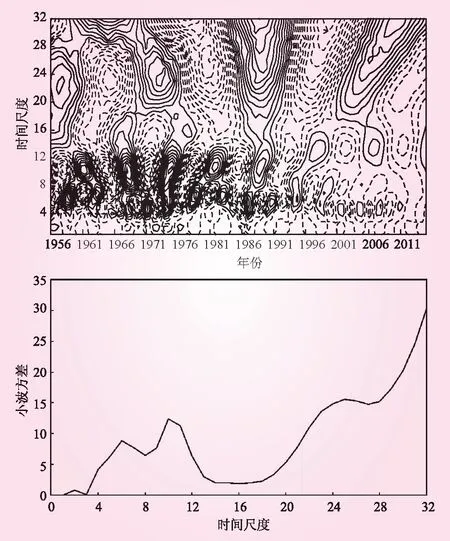
2.3 径流泥沙周期性变化分析
2.4 径流泥沙双累积分析
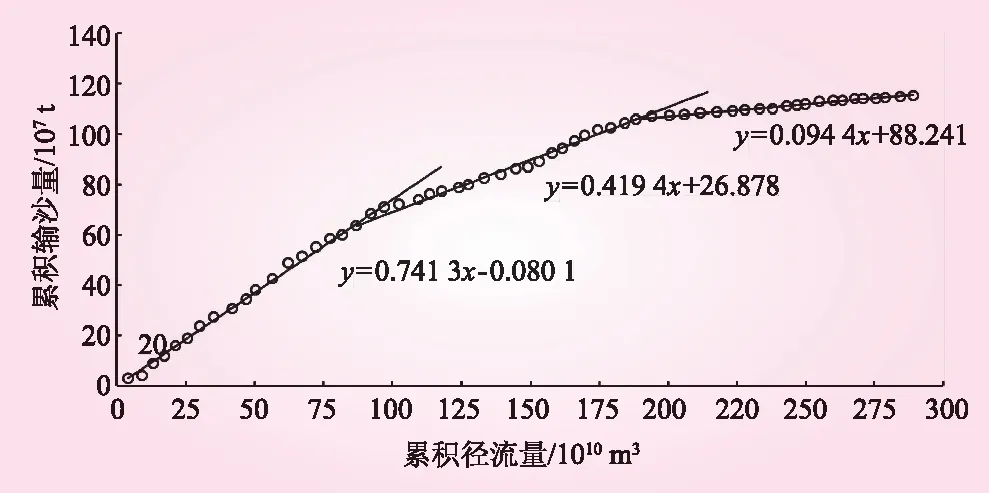
2.5 水沙关系阶段性变化分析
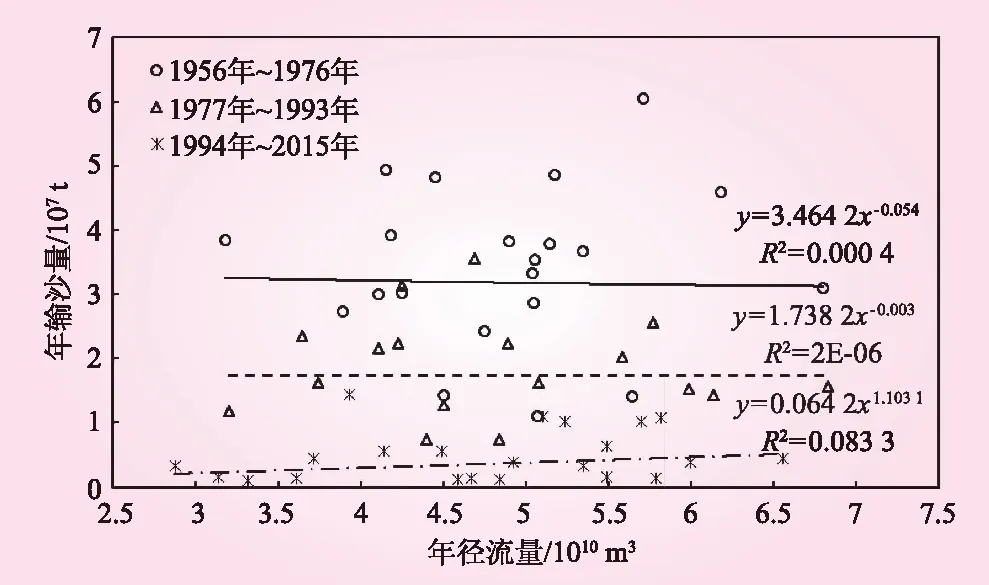
3 径流泥沙演变影响因素
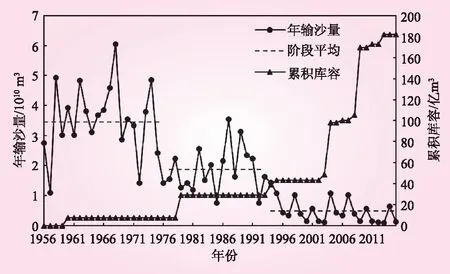
4 结 语

