金纳米颗粒在全血环境中近场增强特性
李俊平,陈娜,刘书朋,陈振宜,庞拂飞,王廷云
(上海大学特种光纤与光接入网省部共建重点实验室,特种光纤与先进通信国际合作联合实验室,上海先进通信与数据科学研究院,上海 200444)
1 引言
当贵金属纳米颗粒(Nanoparticles,NPs)与光相互作用时,如果入射光子频率与贵金属颗粒传导电子的整体振动频率相匹配,纳米颗粒对光子能量产生很强的吸收作用, 这种现象称为局域表面等离子共振(Localized surface plasmon resonance ,LSPR)[1]。贵金属NPs在表面能量发生耦合产生局域电场增强,局域场的产生能够增强介质的线性或非线性响应。贵金属NPs被广泛应用于光子学[2],化学[3],太阳能电池[4],生命科学[5]和生物分析等领域[6]。在生物检测领域,贵金属NPs产生的强局域场可以提高生物分子检测的灵敏度。这种检测灵敏性虽然高,但是依然无法实现在低浓度血药检测和血液中癌症标志物检测上的临床应用。为了提高检测的灵敏性,全面了解贵金属纳米材料在血液环境中的局部电场增强特性以及最大化提高检测灵敏性是非常有必要。
已有研究表明,贵金属NPs的LSPR特性取决于它们的成分,几何参数,空间有序性和周围环境[7]。纳米颗粒所处的周围环境对其共振波长和局域电场增强有所影响,当颗粒所处的环境从水溶液(折射率为1.33)到乙醇溶液(折射率为1.36)时,共振峰发生红移。从水溶液到空气介质(折射率为1.0)时发生蓝移[8]。周围环境不变的情况下,随着金纳米颗粒(Gold nanoparticles,AuNPs)半径的增大,共振峰发生红移。当AuNPs半径为75 nm时,相应的近场强度达到最大值[9]。数值计算为进一步控制LSPR特性提供了明确的指导,有助于探索基础科学新的方面,以满足不同应用场景。
贵金属纳米粒子,如金、银和铜[10]在可见光区域具有较强的近场增强效应。该效应可以强烈放大光学信号,具有大电场增强的耦合系统已应用于拉曼散射信号的增强[11]。AuNPs由于其良好的生物相容性和稳定性被用作生物应用型探针,例如:癌细胞抗原检测、药物分析、细胞内环境监测和生物传感器[6]。2015年上海大学特种光纤实验室陈等人制备表面具有AuNPs基底的光纤纳米探针[11],通过探针体内外检测小鼠血液中药物乳酸左氧氟沙星的浓度变化。其中远程检测乳酸左氧氟沙星的检测限可以达到10-3M。2018年Hoan T. Ngo等人制备银包金纳米立方体直接检测血液裂解液中病原体RNA[12]。在这些应用中,AuNPs所处的介质环境不再是空气或水溶液,而是全血环境。全血是一种相对复杂的介质环境,其主要成分是血细胞,血清和血小板[13]。这些成分对不同的可见光波长具有不同的吸收特性和散射特性,故血液的光学特性对AuNPs的近场特性有所影响。因此,研究全血环境中AuNP的近场增强特性是非常有必要的。据我们所知,尚未研究血液环境中金纳米颗粒的近场特性。我们计算了血液消光系数、建立金纳米颗粒在血液环境中的模型,并采用三维有限元方法系统地分析了共振峰的变化趋势和局部电场强度分布情况。此外,基于仿真结果,分析了全血的消光系数对近场强度的影响。
2 数值仿真
使用COMSOL Multiphysics中RF模块并采用有限元法(Finite Element Method ,FEM)进行近场光强模拟。有限元法是一种用于求解麦克斯韦方程的数值求解方法,即将连续体划分为数目有限的离散单元进行求解,RF模块使用网格剖分实现对求解域的单元化。图1为单个金纳米颗粒在全血环境中的三维模型图,相比于二维模型,采用三维模型更能真实模拟全血环境中AuNP局部电场增强。模型正中间为金纳米球,如图1右上角所示。外层是厚度为250 nm全血环境,AuNP与全血环境区域为计算区域,整个模型处于纳米级别。值得注意的是,实际实验中收集到的散射光是AuNP局域电场通过全血环境(主要为微米级的红细胞)二次散射后获得的,强度会有所减弱。为了计算区域与有耗介质层能够完全匹配,使得电磁场能够无反射进入虚拟有耗介质,本文在全血外层引入厚度为50 nm的完美匹配层(Perfect Match Layer,PML),使得有耗介质层波阻抗和计算区介质波阻抗相等,这样电磁场可以无反射的进入非计算区域。同时PML最外边界被定义为具有散射边界条件。激励源被定义为在z方向上传播,在y方向上偏振的平面波。为了方便计算近场增强和拉曼增强因子,激励源电场强度E0设置为1 V/m。近场增强是指由金纳米颗粒在入射光作用下发生表面等离子体共振产生的局部电场Eloc与入射光电场E0的比值,即Eloc/ E0。
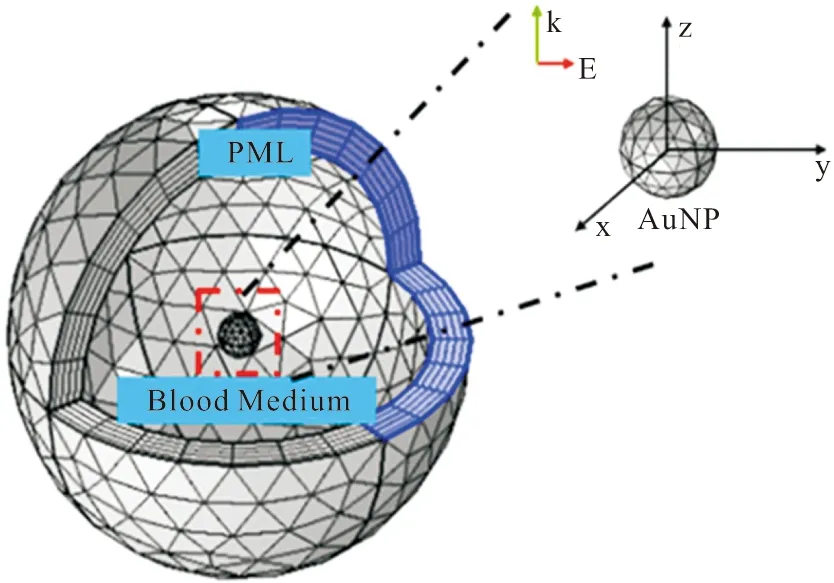
图1 单个金纳米颗粒在血液环境中的模型图Fig. 1 Model diagram of a single gold nanoparticle in the blood environment
LSPR效应的理论模型为当粒子尺度远小于入射波长时,它在任意瞬时都可以看做处于恒定的外电场环境中。因此,可以将系统当做准静态近似从而将Helmholtz方程简化为Laplace方程。模型中粒子颗粒大小为55 nm,入射光波长范围在可见光至近红外,远大于金颗粒,满足LSPR效应理论模型。在入射场E0作用下,金颗粒发生极化,因而可以等效为一个偶极子,其中α为粒子的极化率。在准静态近似理论下,极化率α可以表示为[14]
(1)
式中,R为金属粒子的半径,εm为周围环境的介电常数,也可以用折射率表示,ε(ω)为金属粒子的等效复介电系数。根据散射截面定义,散射截面是σs为散射强度与入射强度的比值:
(2)
考虑金属粒子介电常数的Drude模型[14]:
(3)
其中,ωp表示金属的等离激元频率,取决于金属的电子密度,Γ为阻尼系数,令Γ足够小,由共振条件可以得到金属粒子的局域表面等离激元共振频率ωlsp。公式4表明局域表面等离激元共振频率与金属纳米颗粒的形状和尺寸以及周围环境都有关。
(4)
3 结果与分析
3.1 全血复折射率
本文模型中所建立全血介质层取决于血液的光学特性,其中包括折射率和消光系数。折射率是血液复折射率的实部,消光系数是虚部。血液是一个非常复杂的环境,其消光系数和折射率主要受红细胞中血红蛋白影响[15],含有氧的血红蛋白占总血红蛋白的比例称为氧饱和度(Oxygen Saturation ,SO2)。医学研究人员通常考虑SO2= 0%和SO2> 98%两种方式确定血液吸收系数。本文研究中,基于文献[16]提出的方法获得在可见光到近红外波段下全血的折射率和吸收系数部分数据。进一步通过公式5将吸收系数α(λ)转换为数值模拟所需的消光系数κ(λ)。其吸收系数通过积分球光谱仪测量菲涅尔反射,折射率是通过将Kramers-Kronig分析与散射理论相结合计算得到的[17]。全血复折射率的实部和虚部如图2所示,在450 nm左右波长下,其复折射率实部和虚部都达到最大值,实部高于1.40,虚部高于0.005,高于600 nm波长的折射率基本保持不变。SO2= 0%与SO2> 98%的折射率受波长影响的整体趋势一致,折射率相差不大。
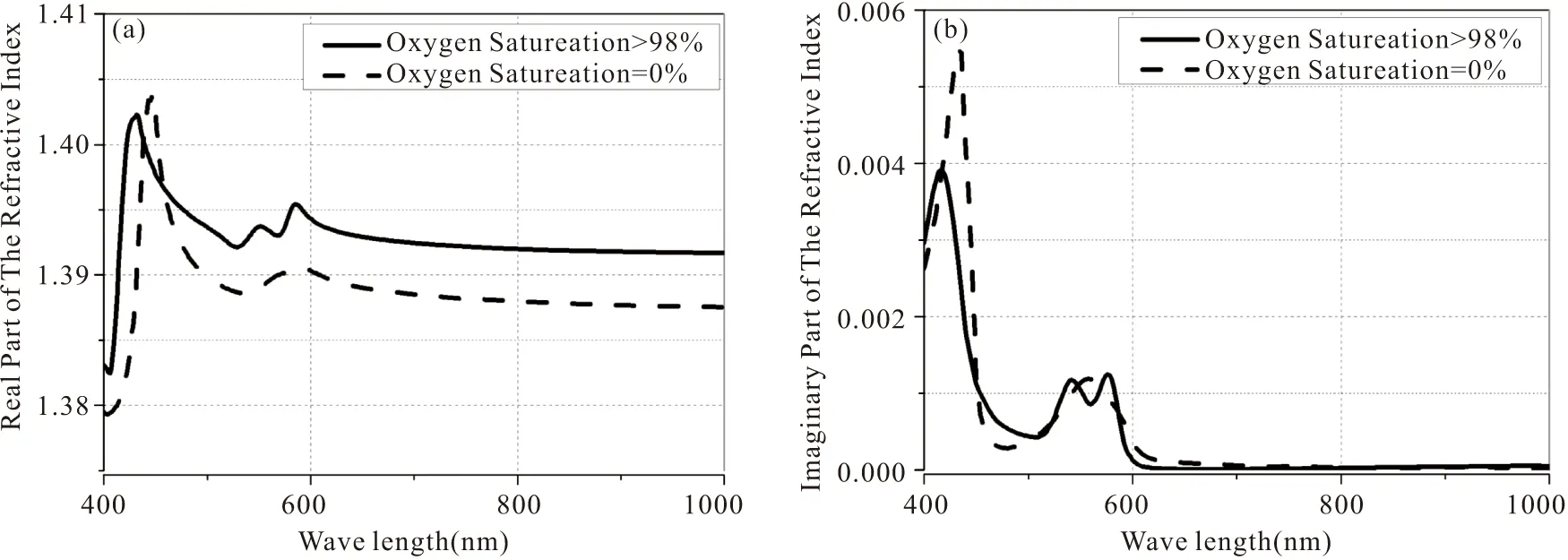
图2 氧饱和度等于0%和大于98%情况下全血的复折射率。(a)复折射率实部(原始数据来自文献[16]);(b)复折射率虚部Fig. 2 The complex refractive index of whole blood in SO2=0% and SO2>98%. (a) The real part of refractive index (Original data comes from the literature[16]), (b) The imaginary part of refractive index
(5)
3.2 单个金纳米颗粒在全血环境下的近场增强
为了研究全血环境中单个金颗粒等离子体共振波长和增强强度,建立了如上图1所示的模型。其中金纳米颗粒尺寸为55nm,这与实际实验中通过还原法制备的金颗粒尺寸相同[18]。图3(a)是单个金纳米颗粒在入射波长为633 nm下y-z平面的近场分布特性图,由于金纳米的LSPR效应使得表面的电场强度得到较大的增强,越靠近球表面电场强度越强。从理论上可知(公式(1-3)),金纳米颗粒的LSPR效应与粒径和激发光波长有关,对图1模型进行波长在500~650 nm扫描,并研究金纳米颗粒尺寸大小对近场分布的影响。如图3(b)所示,粒径大小为30~100 nm时,其共振波长在500和650 nm之间。从图中可以看出,随着粒子尺寸的增大,共振波长红移,这与文献[19]基本一致。表格1是不同粒径的金纳米的共振峰和相应的近场强度。当粒径为80 nm时,共振波长为580 nm,电场强度为7.65 V/m,拉曼增强因子为3.44×103。拉曼增强因子表达式可以简化为| Eloc|4[10]。当粒径小于80 nm时,随着粒径增加,电场增强。当粒径大于80 nm时,随着尺寸增大,电场强度减弱。模拟结果表明粒径为80 nm时,局部增强效果最好。可以通过改变金纳米颗粒的大小调节LSPR的共振峰。

图3 在全血环境中的金纳米颗粒的近场分布特性以及在不同直径下局域电场分布。(a) 在633 nm入射波长下金纳米颗粒的近场特性分布;(b) 金纳米尺寸在30-100 nm,波长范围为500-650 nm下的局部电场Fig.3 Near-field distributioncharacteristics of AuNP in whole blood environment and local electric field distribution at different diameters (a) Near-field characteristic distribution of AuNP at an incident wavelength of 633 nm; (b) Local electric field with a gold nanometer size of 30-100 nm and a wavelength range of 500-650 nm
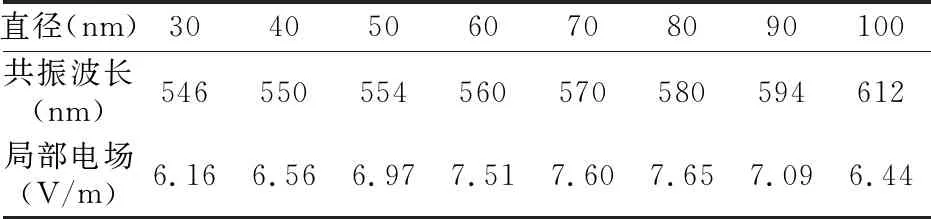
表1 不同粒径下的共振波长和局部电场Table.1 Resonance wavelength and locally electric field under different particle size
相比于空气介质,金纳米颗粒在全血中的增强情况和消光系数对近场增强的影响也需要进一步研究。在粒径为55 nm情况下,改变不同介质环境的折射率参数,其中空气的折射率设置为1,其他条件不变。图4(a)比对了不同环境介质对近场增强的影响,在空气中的金纳米颗粒共振峰位置为530 nm,电场强度为4.6V / m,拉曼增强因子为4.47×102。在全血中的共振峰位置为558 nm,电场强度为7.5 V/m,拉曼增强因子3.16×103。与空气相比,共振峰右移了28 nm,拉曼增强因子提升一个数量级。在近场收集的情况下,表明待测分子在血液中检测灵敏度有可能高于在空气中。全血不同于其他介质环境,例如水,空气等,因为它在不同波长具有对光的吸收特性,从而削减光信号。图4(b)中虚线代表在540 nm到570 nm波长范围内无消光系数模型中计算出的曲线,实线是具有消光系数的曲线,且两者其他条件一致。通过比较可知,全血的消光系数对局部电场的影响非常小,局部电场增强差异小于0.1 V/m。全血环境介电常数εm与全血的复折射率关系如公式6所示。其中,n(λ)为折射率;k(λ)为消光系数,与吸收系数成正比,指吸收光强的能力。血液的消光(吸收)系数会削弱入射光的强度,与纳米颗粒直接接触的光强减弱,导致局部电场减弱。在图2(b)中,血液的消光系数在540~570 nm波长下均小于0.002。相比于血液折射率(>1.39),0.002的消光系数相对较小,导致近场光强削减不明显。这可能是局部电场增强差异小于0.1 V / m的原因。
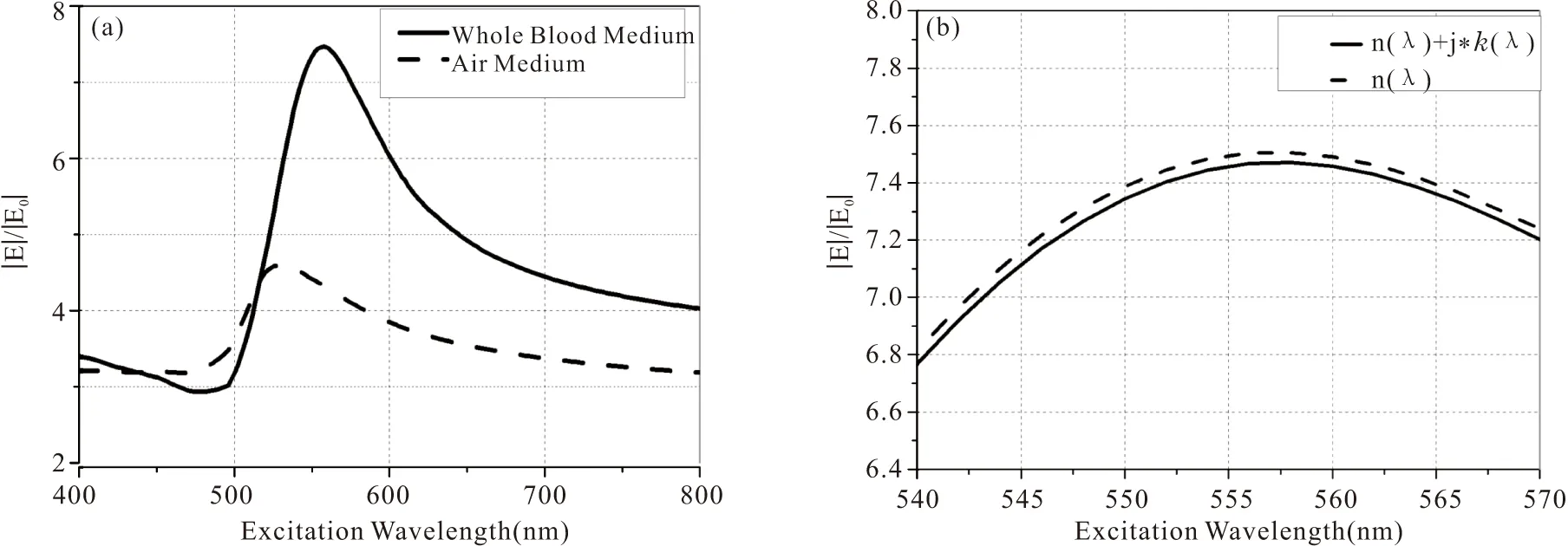
图4 在不同介质中距离金纳米颗粒表面1 nm处的电场值。(a)在空气和全血环境;(b)在全血介质中,折射率无消光系数k(λ)Fig.4 Electric-field values located 1nm away from a single nanoparticle in the different mediums. (a) In air and whole blood medium. (b) In whole blood medium that the refractive index without extinction coefficient k(λ)
εm=(n(λ)+j*k(λ))2
(6)
3.3 双金纳米颗粒在全血环境下的近场增强
在现实应用中,电场的增强或拉曼信号的增强不单单是单个颗粒产生的,还存在多个粒子之间的相互作用,我们对两个粒子之间的近场耦合进行了研究。影响局部电场增强的主要因素是两个金纳米之间的间距,本文模拟了双金纳米粒子在间距1 nm到12 nm的拉曼增强因子和共振峰。模型如图5(a)所示,直径都为55 nm的金纳米粒子位于其中,只改变两个粒子的距离,其他条件与图1一致。由于两粒子间的近场耦合,在两球之间区域产生大的局部电场,‘热点’区域位于两个粒子之间。图5(b)是在波长范围500~800 nm之间,两个AuNPs间距对共振波长和局部电场的影响。当间隙为1 nm时,产生两个共振峰,其中在575 nm处的侧峰是由四极子产生的,700 nm处是由偶极子产生的。从图6可知,随着间隙增大,共振峰蓝移并且拉曼增强因子减弱。从间距为1 nm和12 nm比对可知,虽然间隙仅仅变化11 nm,但增强因子存在巨大差异。当间隙为12 nm时,其增强因子为105且共振峰为582 nm;当间隙为1 nm时,拉曼增强因子可高达到1011,比间隙为12 nm时高达6个数量级。因此很大可能性上可以高灵敏度地检测全血环境中的低溶度分子拉曼信号。
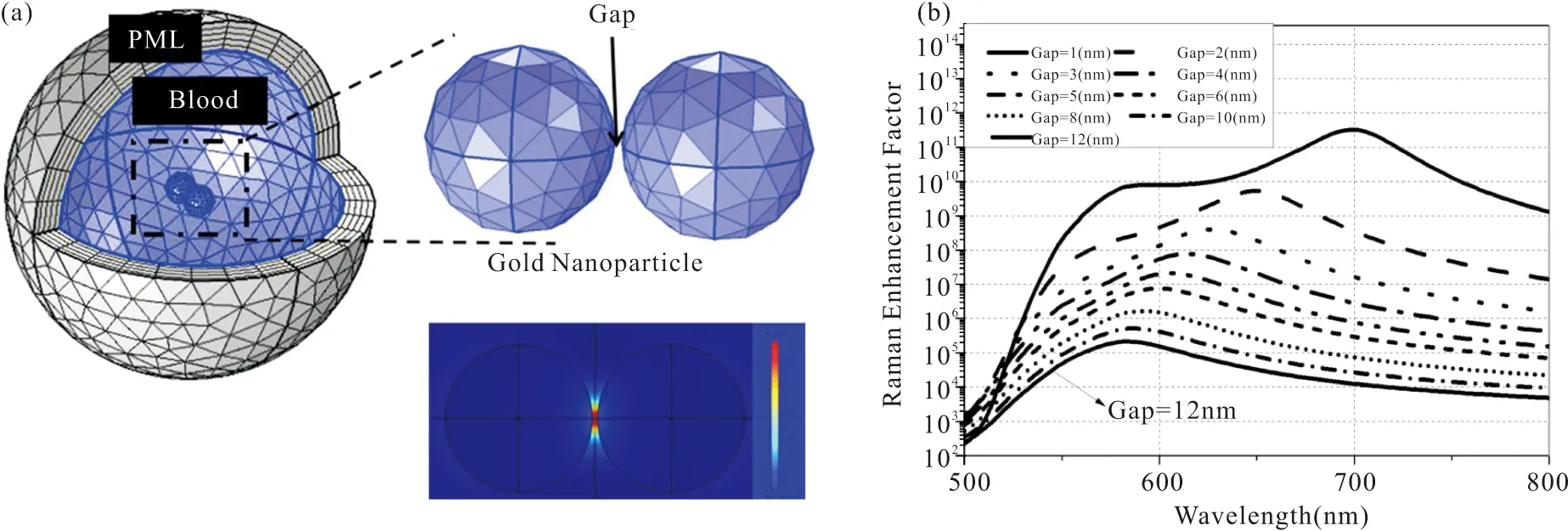
图5 全血中双金纳米颗粒模型及拉曼增强因子随间距的变化情况。(a)双金纳米颗粒在全血环境中的模型;(b)在500~800 nm波长范围内双金纳米颗粒之间的拉曼增强因子随间距的变化情况Fig.5 Double AuNPs model inwhole blood and Raman enhancement factor as a function of gap distance. (a) The model of double AuNPs in the blood environment; (b) The variation of the Raman enhancement factor between the double AuNPs at 500-800 nm with the different gap
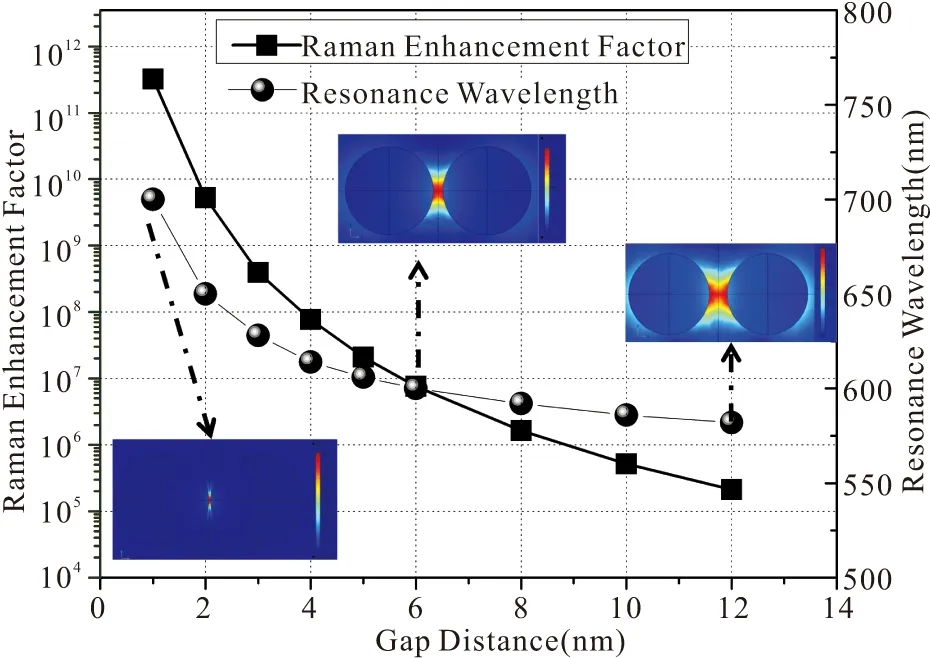
图6 共振波长和拉曼增强因子随两个AuNPs间距的变化Fig.6 The resonance wavelength and Raman enhancement factor varied with the distance between thedouble AuNPs
4 结论
在这项工作中,我们考虑了全血的吸收和散射特性,建立了在全血环境中AuNPs模型,并通过FEM方法研究了AuNPs在全血环境中的近场增强特性,系统地分析了共振峰位的变化趋势和局部电场强度。通过调节金纳米颗粒的尺寸和颗粒之间的间距来提高局部电场,从而可以激发更强的生物分子信号,提高检测灵敏度。一方面表明在全血环境中,金纳米颗粒直径为80 nm时,电场强度最强。两纳米颗粒间距为1 nm时,拉曼增强因子可高达1011。另一方面表明全血的消光系数对金颗粒近场增强影响不大,可以忽略。该方法不仅可用于研究全血中其他贵金属材料的近场增强效应,也为提高纳米颗粒在血液环境中的性能提供参考。

