基于安德森加速的快速B样条拟合算法

秦文杰，张举勇

基于安德森加速的快速B样条拟合算法

秦文杰，张举勇

(中国科学技术大学数学科学学院，安徽 合肥 230026)

曲线拟合技术已被广泛地应用于图像处理、工程实验等领域。其中，B样条曲线拟合是曲线拟合中最常见的方法，它具有局部性好、连续性好等优点，但拟合精度一般较低。在实际应用中，B样条曲线拟合对于精度和速度的要求都较高。为了提升平面B样条曲线拟合速度，将安德森加速的想法应用到曲线拟合的方法之中，提出一种基于安德森加速的拟牛顿方法。首先设定一个初始形状，然后根据初始形状找到其每个数据点的投影点的位置参数，然后利用安德森加速计算出控制点的相应位置，迭代进行以上2步，直到结果收敛。实验结果表明，该方法在收敛速度和迭代时间上均优于其他方法。

B样条拟合；安德森加速；拟牛顿方法；曲线拟合；样条逼近

曲线拟合问题一直是计算机图形学中重要的组成部分，而随着计算机科学与工程技术的发展，B样条拟合问题更成为曲线拟合中的热点问题。在实际的工程应用中，一般获取到的初始数据往往是无序的点云数据，因此，如何拟合无序数据点是一个重要的问题。本文主要讨论如何对平面无序数据点进行快速的B样条曲线拟合的问题。

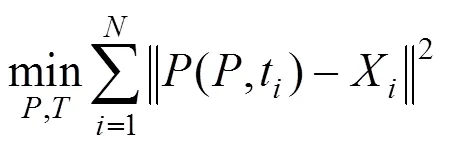
其中，(,t)为为在拟合曲线上距离点X最近的点，也称作投影点。

1 相关工作

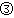
1.1 经典的B样条曲线拟合算法

对于绝大多数B样条曲线拟合方法，迭代的处理方式均采用了分别计算投影点和控制点的想法：

(1) 投影点计算，即固定当前的曲线控制顶点不变，计算出数据点在当前曲线上的投影点。在计算投影点时往往会受到正交性的约束。

(2) 控制点更新，在此步骤中投影点的位置参数是固定的，可用一个二次函数E来近似数据点与拟合曲线之间的距离关系，则优化该二次目标函数的能量就可以得到对应的新的控制点位置，即求解一个线性方程组。而相对应的，不同的二次函数E的取法其实也对应了不同的方法。

对应的是SDM方法[6]。其中，为点(t)处的曲率半径；为X与(t)间的距离值，以正负号来表示其方向。从能量定义的方式可以看出，该方法包含了二阶导数的信息与曲率信息，因此，与前2种方法相比，其更接近于真实的距离平方函数。同时，在优化方面，SDM方法是一种拟牛顿方法，其修正了Hessian矩阵，使之保留了与几何性质相关的简单部分，同时在修正的过程中保证了Hessian矩阵的半正定性。文献[6]证明了SDM方法在收敛速度和稳定性方面明显优于PDM和TDM方法。

L-BFGS方法[7]更多地将注意力放在了优化求解速度上。其与传统方法的区别在于，在迭代求解的过程中，可通过求出近似的逆Hessian矩阵而避免了矩阵计算，并同时优化了投影点与控制点的信息。因此，该方法在收敛速度上要远远优于其他3种方法。

SDM方法和L-BFGS方法均属拟牛顿法，但存在一些区别。如L-BFGS方法能够在每步迭代当中同时优化控制点位置与投影点参数，并且不需要求解任何线性方程组，因此该方法比其他方法效率更高。

在传统的B样条曲线拟合方法中，PDM方法收敛速度较慢；TDM方法本质上是高斯-牛顿法，因此具有不稳定的特点。SDM方法是一种拟牛顿法，利用近似的Hessian矩阵代替真实的Hessian矩阵，在稳定性和收敛速度之间找到了很好的平衡；L-BFGS方法也是一种拟牛顿方法，通过每一步推导近似的逆Hessian矩阵来达到自己优化加速的目的。

1.2 局部-全局求解器

由于局部-全局求解器在近似求解最优化问题上的高效表现，其在图形学的各个领域均有广泛地应用。文献[8]提出了ARAP方法，即通过最小化目标能量来进行曲面建模；文献[9]也应用了该方法来进行保形或保角的三角网格参数化工作；文献[10]也使用了局部-全局求解器的框架对弹簧进行了快速并且接近真实的模拟。

与此同时，针对局部-全局求解器的结果收敛到高精度时耗时过长的问题，许多改进工作被陆续提出。SORKINE和RABINOVICH[11]采用Cheybyshev方法来实现收敛的加速；文献[7]提出了L-BFGS方法，速度比普通的局部-全局求解器更快。本文工作重点在于优化局部-全局求解器。

1.3 安德森加速

安德森加速被广泛地应用于各个领域，该方法能够加快求解迭代问题的收敛速度。其最初由ANDERSON[12]提出，随后PULAY[13]在量子化学的计算中引入了同样的技术。近年来，越来越多的研究者开始关注该方法在数值计算中的应用。文献[14]用安德森加速来加速求解平流扩散问题，文献[15]用其来求解低秩张量近似的问题，文献[16]用来加速几何优化与物理模拟问题的求解。

文献[16]与本文的工作想法类似，但并不完全相同。前者提出了一种统一的、全新的安德森加速的应用思路，即对于固定点迭代问题，用安德森加速进行优化，并举了几何优化与物理模拟 2个例子进行说明。但其求解的问题往往是单变量的问题，本文通过引入辅助变量，使得问题能够用局部-全局求解器迭代求解。由于辅助变量由人为引入，所以辅助变量与待求的变量之间关系简单，能够很容易将问题改写为固定点迭代的格式。而在B样条曲线拟合的问题中，投影点位置参数与控制点之间具有较复杂的关系，也是2个工作的区别所在。

2 算法

2.1 迭代求解的一般方法

已经知道B样条曲线拟合问题可以化为以下最优化问题

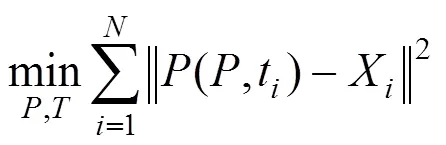
一般分为2个步骤：

步骤1.投影点计算，即保持当前拟合曲线的控制顶点不变，计算出关于数据点{X}的对应位置参数={t}，使得点序列{(t)}均为当前拟合曲线上{X}的投影点。该步骤需要满足

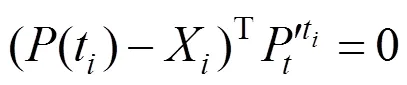
步骤2.控制点更新，位置参数={t}被固定，即B样条的系数矩阵

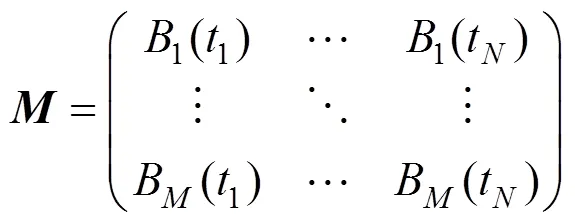
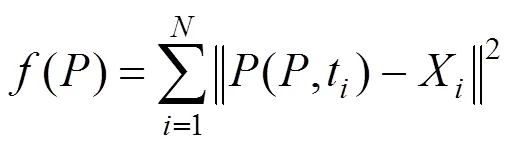
2.2 安德森加速

为了加速迭代过程的收敛，首先要意识到在投影点计算的步骤中，待求的位置参数={t}所对应的矩阵可以表示为当前控制顶点{(t)}的函数，所以将投影点计算与控制点更新结合起来，可以将该问题看成固定点迭代问题，即

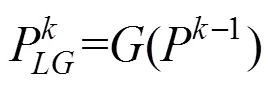
对于此问题而言

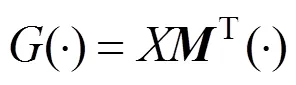
对于固定点迭代问题，其残差为

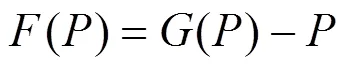
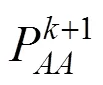
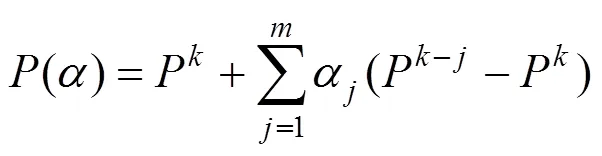
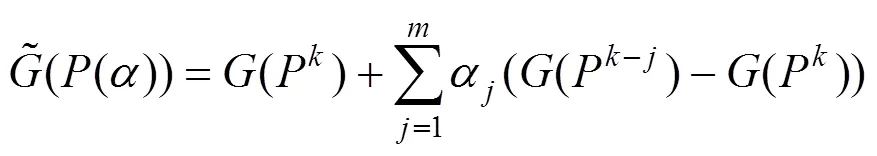
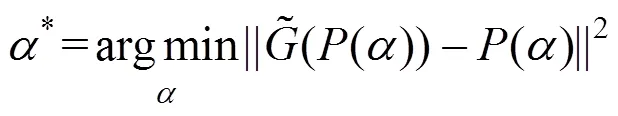
在第步迭代中，本文得到了以上结果，那么对于第+1步的结果，有

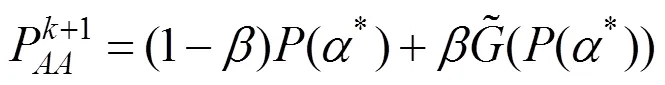
其中，为混合参数，在绝大部分文献中，通常有=1，本文也依此取值。

需要注意的是，最小二乘问题也可以写成如下形式

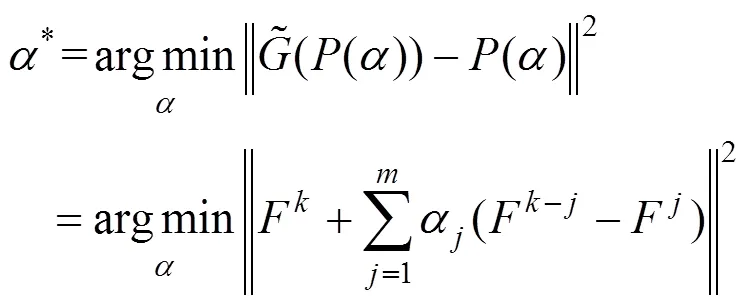
在求解最小二乘问题时，需要在每一步迭代中都重新计算所有的残差，明显影响效率，因此可以采用文献[17]的做法，通过构造法向方程使得效率变高。

2.3 稳定性保证

若存在迭代起始位置靠近真解的情况时，文献[18]已经证明安德森加速在弱条件下收敛。而与此同时，也存在起始位置距离最后的真解很远的情况，在该情况下，安德森加速可能会变得不稳定，可能会出现收敛速度缓慢或是收敛到局部解的情况。

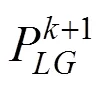
2.4 m的选取

根据以上对于算法的解释可以知道，用于加速的先前的迭代次数对于算法的性能有着较大的影响。当取值较大时，更多的信息被用于近似逆Jacobian矩阵，通常会使收敛速度变快。但另一方面，过大的也会造成每一步迭代的计算成本增加，并有可能导致过拟合。本文经过试验发现，超过6以后对收敛速度影响有限，与文献[16]的经验一致。在本文中，取5。具体试验方式为：对于若干例子，将值取1~6进行试验，得到如图1所示的对比，可以直观看出的取值对收敛速度的影响。事实上，是一个需试验得到的相对最佳值。

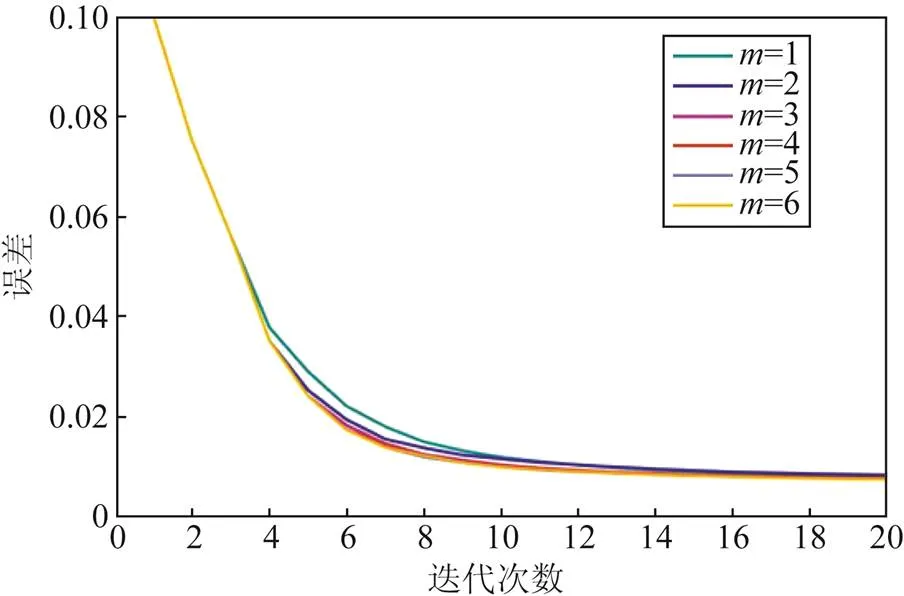
图1 m不同取值对比图

2.5 算法流程

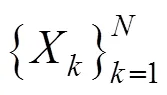
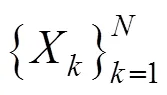
步骤2.对于每个数据点X找到其投影点的位置参数，从而确定出初始的位置参数。

步骤3.计算P+1，其中=1,2,...。

步骤3.2.比较目标能量，根据结果修改相应P，值，修改原则可见2.3节。

王鹤鹏[4]等在基于VR技术的汽车拆装实训课程教学改革探索中认为，VR技术的应用可以有效解决实训场地要求较大，试验材料及教学成本较高且存在一定事故隐患等问题。蒋斌[5]在发动机拆装实训课程中引入翻转课堂的教学方法。李军功[6]在发动机构造与拆装实训课程的教学中采用项目教学的方法。

步骤3.3. 计算P，求解相应的最小二乘问题，求出P+1。

步骤4.重复步骤3直到能量收敛。

在实际应用中，初始曲线一般由人为确定，本文中采用圆形、椭圆等形状。对于步骤3中计算投影点的–步骤，参考了文献[7, 19]。需要注意的是，在本文的模型中，并未引入相应的光滑项。

3 实验结果及分析

3.1 实验的相关定义与参数

首先对每一步的拟合误差给出定义，对于第步，拟合误差为

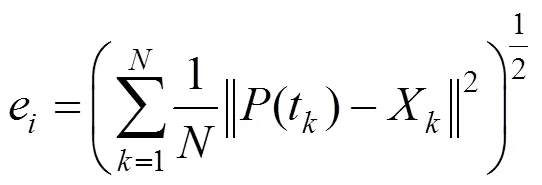
该函数是在稳定性保证过程中需要比较的目标函数。

在本文的实例中，B样条曲线的参数域为=[0,1]，所有曲线拟合数据点都会被缩放至包围盒[0,1]×[0,1]中。

同时，由于文献[7]中已经有了L-BFGS方法与其他经典方法的完整比较，因此在本文中，只与L-BFGS方法作对比。L-BFGS方法的值取5，与文献[16]保持一致，同时，不添加光滑项。本文方法与L-BFGS方法均采用C++编写，L-BFGS方法的具体实现可参考文献[16]。

同时，所有操作均在如下配置下进行：Intel® Core™ i5-8050U @ 1.60 GHz，1.80 GHz，8.00 GB。

3.2 实验对比

对比3个实例，并展示最终结果、误差-时间关系图、误差-迭代步数关系图(图2~4)，及统计最终收敛的总时间与每一步迭代需要花费的时间 (表1~3)。

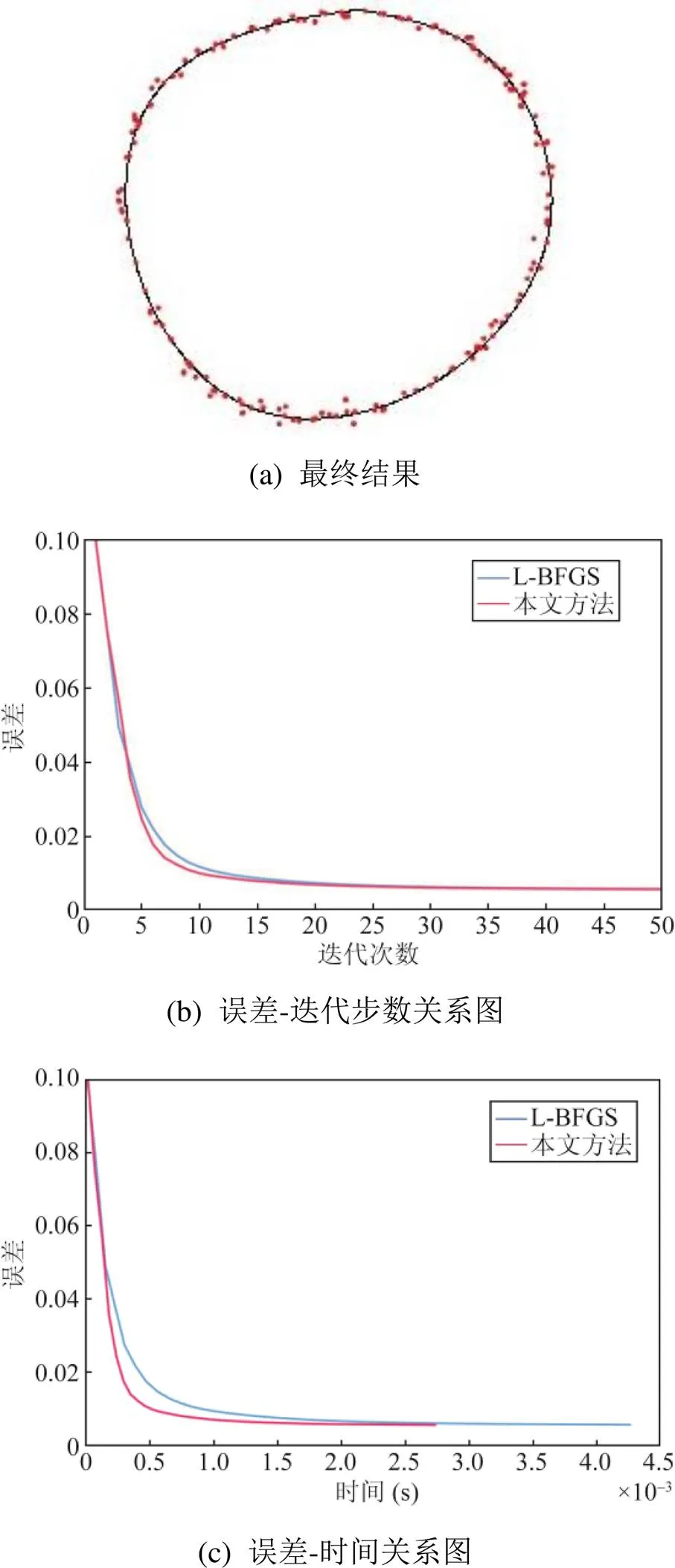
图2 拟合曲线实例1 (8个控制顶点，100个数据点)

表1 实例1收敛总时间及迭代平均时间(s)

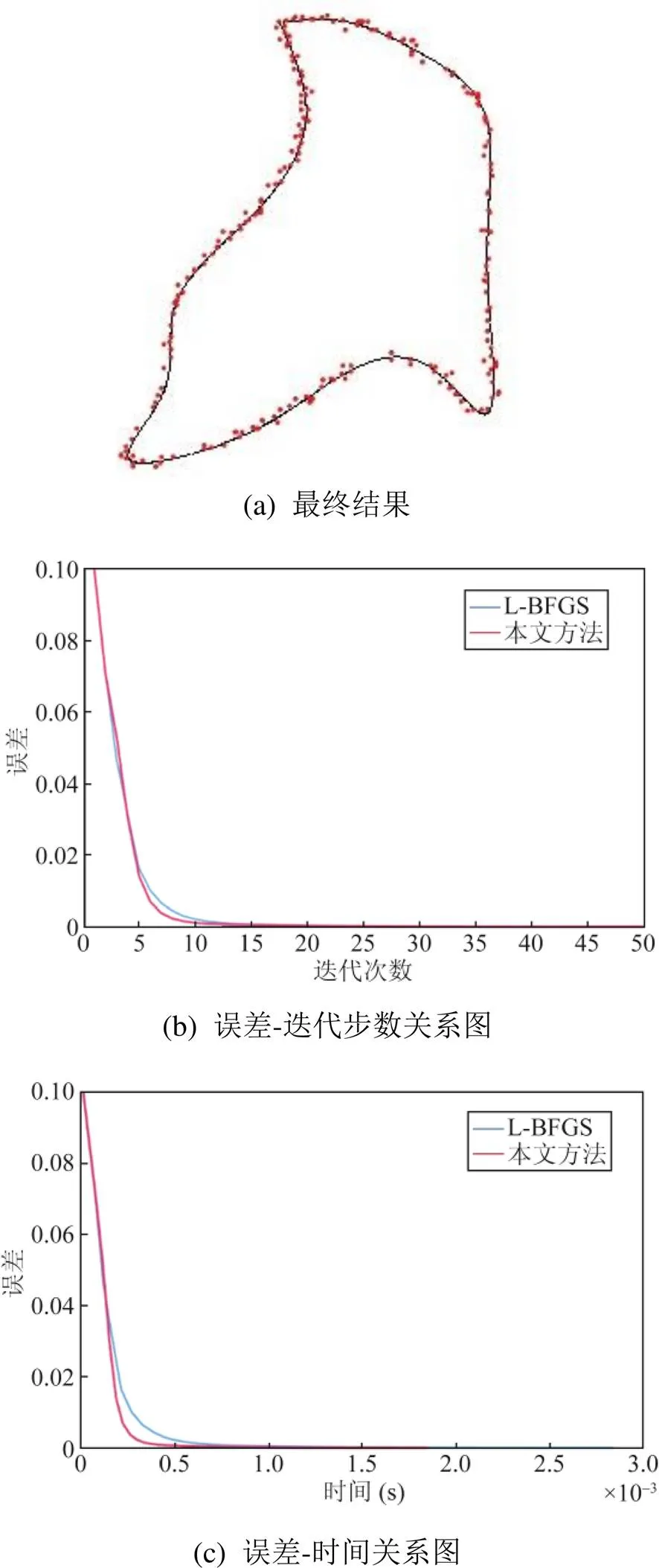
图3 拟合曲线实例2 (20个控制点，90个数据点，包含尖锐特征)

表2 实例2收敛总时间及迭代平均时间(s)

由3个例子可以看出，在最初的几步迭代过程中，L-BFGS与本文方法的效果接近，原因是这 2种方法都需要前步的结果用来优化近似之后的结果，在最初的迭代中2种方法都没有使用各自的优化思路。在之后的迭代中，安德森加速的收敛速度要快于L-BFGS方法，两二者在每一步迭代上所花费的时间基本保持在同一量级。

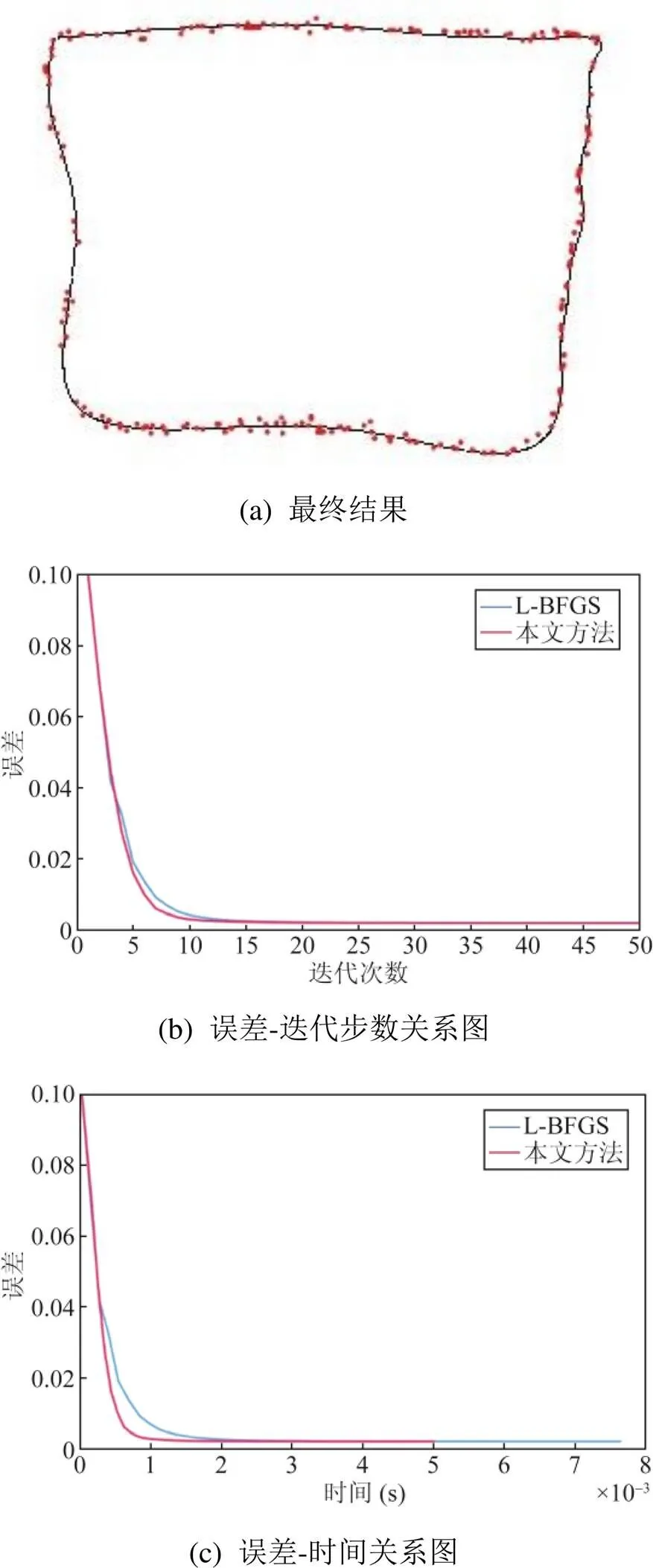
图4 拟合曲线实例3 (8个控制顶点，200个数据点，存在噪音数据点)

表3 实例3收敛总时间及迭代平均时间(s)

同时，从收敛效果上来看，拟合误差是衡量收敛效果的指标，在相同的收敛时间中，本文方法的拟合误差结果总是小于L-BFGS方法。

3.3 单步迭代时间稳定性

3个实例的数据点的个数都在102量级，为了更好地比较算法的稳定性，更希望看到在较大数据点个数下L-BFGS算法与本文算法的表现。因此，对于实例1进行了加点处理。加点原则为：对于每一个已有的数据点，在以其为中心、大小为[0,]×[0,]的包围盒内，随机取个点作为新的数据点；取=5×10–2。

从图5和图6中不难看出，对于L-BFGS算法和本文方法，在误差允许的范围内，每一步的迭代平均时间与数据点的个数成线性关系，且每一步的迭代时间与控制点的个数也成线性关系。由文献[7]可知，传统的拟合方法如PDM，TDM和SDM方法，其平均迭代时间随着控制点和数据点数目的增大而快速增长。

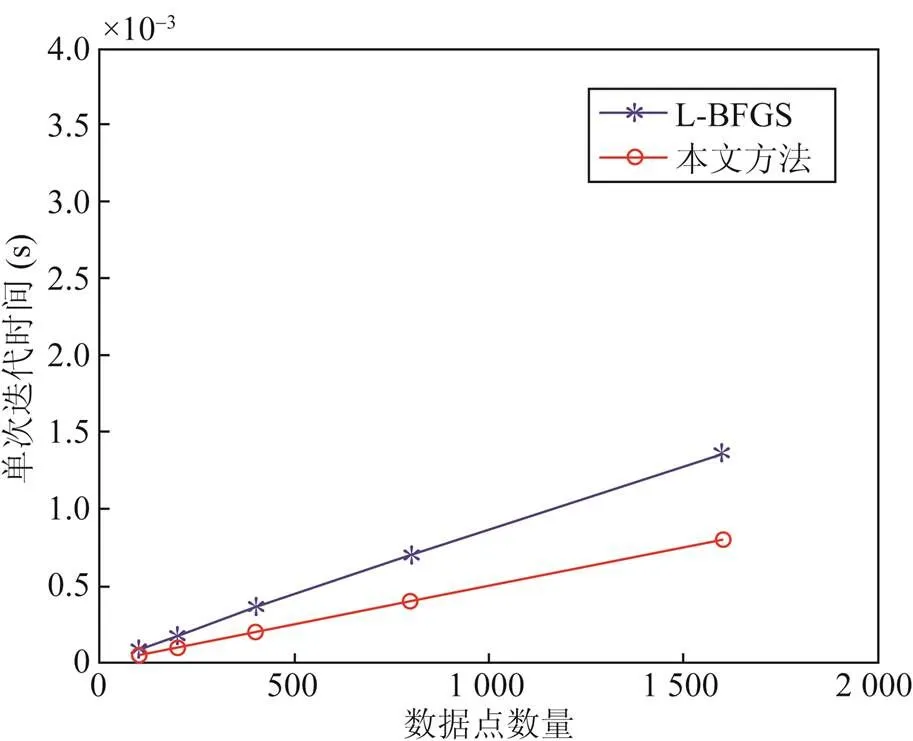
图5 拟合曲线实例4 (8个控制点，数据点个数依次为100，200，400，800，1 600)

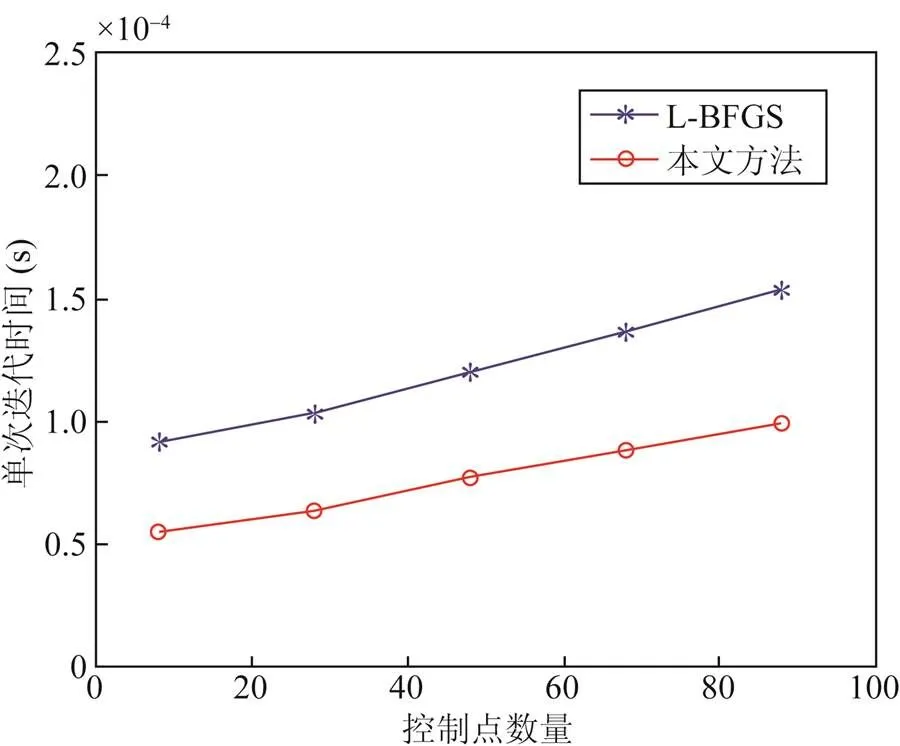
图6 拟合曲线实例5 (100个数据点，控制点个数依次为8，28，48，68，88)

因此，L-BFGS方法与安德森加速方法都有着更适用于大型拟合问题的优点，尤其是控制点较多并且数据点个数较大时，相比其他方法，这2种方法有着较大的优势。

3.4 初值稳定性

算法所取的初始曲线对于算法的效率所造成的影响也是本文所关心的问题。因此，对于实例1，取3种不同的初始曲线进行测试，如图7和图8所示。

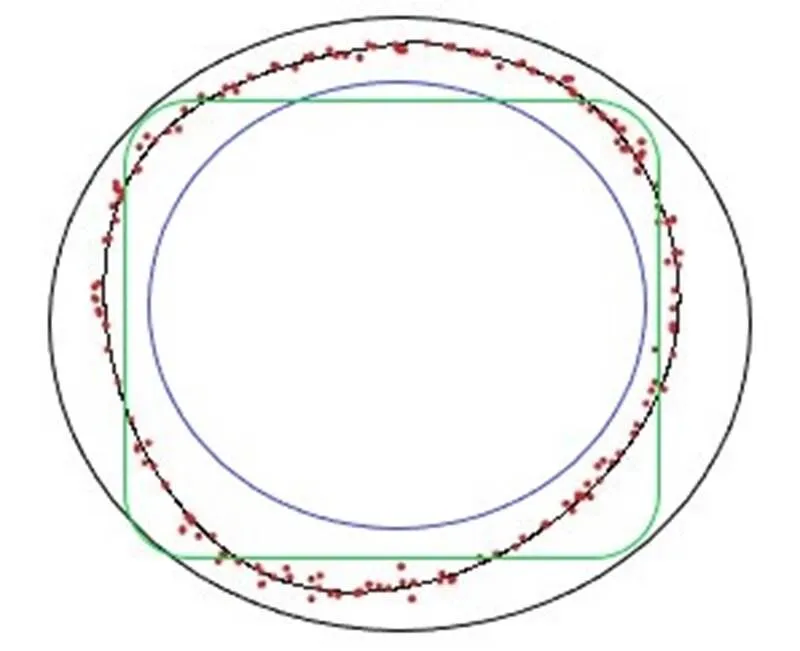
图7 3种不同初始曲线

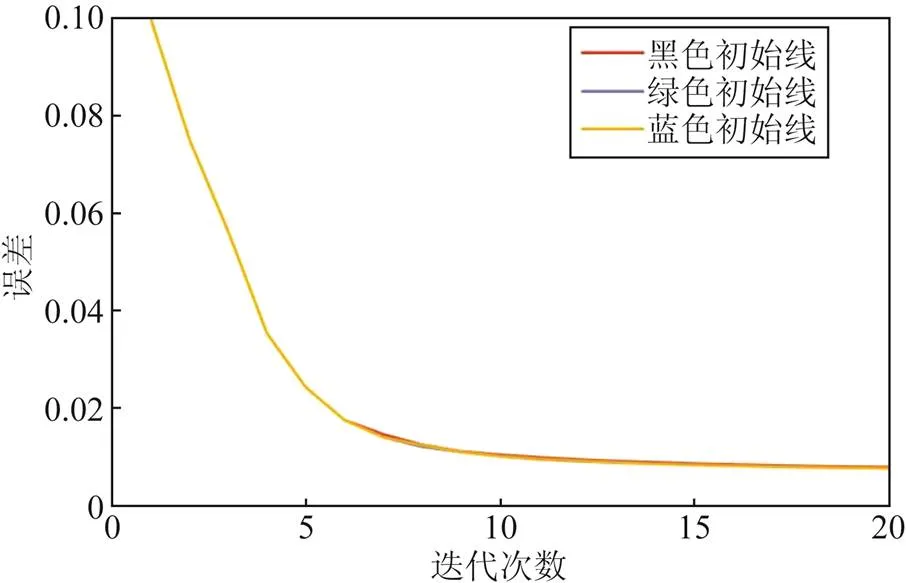
图8 3种不同初始曲线收敛情况

从图8可以看出，不同的初始曲线对于最终收敛情况的影响较小。

3.5 算法分析

从上文实例可以看出，和L-BFGS方法一样，安德森加速方法的计算速度要明显优于一阶的方法，同时，也比L-BFGS方法快一些。

文献[16]和文献[19]已证明了安德森加速是一种用于求解以下非线性方程的拟牛顿方法，即

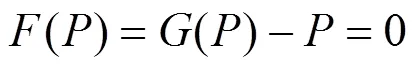
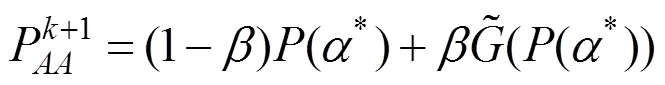
等价于

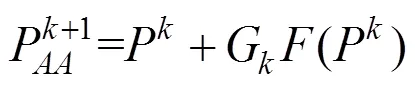
其中，G为在P处的逆Jacobian矩阵的近似。

类似的优化策略在L-BFGS方法中也可以看到，因此L-BFGS方法与安德森加速方法都明显优于一阶方法。在L-BFGS方法中，先为L-BFGS求解器构建初始的下降方向。其求解器的目标是搜索方程()=0的根，其中，为目标能量函数的梯度。在每一个迭代过程中，均需先计算下降方向并进行线搜索来确定下一次迭代。

为了计算下降方向，L-BFGS方法从初始估计-(P)开始计算，其中，是目标函数的逆Hessian矩阵的近似，然后用two-loop recursion算法的步骤来更新出新的逆Hessian矩阵的近似与下降方向。

从以上解释可以看出，L-BFGS方法构造初始逆Hessian矩阵的思路与本文在求解过程中构造逆Jacobian矩阵的思路类似。2种方法的区别就在于构造逆矩阵的方式的不同。在L-BFGS方法中，是基于two-loop recursion算法通过求解次割线方程来更新相应逆矩阵，而本文方法中并没有2步的循环求解的操作。因此，L-BFGS方法在每一步中会有3次点积的操作，而本文方法只需要次，在计算效率上略优于L-BFGS 方法。

4 结束语

本文提出了一种利用安德森加速来进行曲线拟合的方法。该方法本质上是一种求解非线性系统的拟牛顿方法，与传统曲线拟合方法(如TDM，PDM等)相比，不需要在每一步迭代过程中花费大量时间重新进行投影点计算，因而节约了大量的时间。与同为拟牛顿方法的L-BFGS相比，由于在每一步迭代过程中加入的目标能量判断，使得该方法拥有更快的收敛速度。

本文的方法也有一些不足，比如没有加入类似SDM方法中的光滑项，原因是积分形式的光滑项约束很难写成稳定的矩阵形式参与迭代过程。因此，在今后的工作中，期望可以添加合适的光滑项，使得结果更加鲁棒，同时，也考虑将该方法应用到曲面拟合的优化当中。

[1] HOSCHEK J. Intrinsic parametrization for approximation[J]. Computer Aided Geometric Design, 1988, 5(1): 27-31.

[2] PAVLIDIS T. Curve fitting with conic splines[J]. ACM Transactions on Graphics, 1983, 2(1): 1-31.

[3] PLASS M, STONE M. Curve-fitting with piecewise parametric cubics[C]//Proceedings of the 10th Annual Conference on Computer Graphics and Interactive Techniques-SIGGRAPH’83. New York: ACM Press, 1983: 229-239.

[4] SAUX E, DANIEL M. An improved Hoschek intrinsic parametrization[J]. Computer Aided Geometric Design, 2003, 20(8/9): 513-521.

[5] BLAKE A, ISARD M. Active contours[EB/OL]. [2020-03-29]. https://link.springer.com/book/10.1007/ 978-1-4471-1555-7.

[6] WANG W P, POTTMANN H, LIU Y. Fitting B-spline curves to point clouds by curvature-based squared distance minimization[J]. ACM Transactions on Graphics, 2006, 25(2): 214-238.

[7] ZHENG W N, BO P B, LIU Y, et al. Fast B-spline curve fitting by L-BFGS[J]. Computer Aided Geometric Design, 2012, 29(7): 448-462.

[8] SORKINE O, MARC A. As-rigid-as-possible surface modeling[C]//Proceedings of Eurographics/ACM Siggraph Symposium on Geometry Processing. New York: ACM Press, 2007: 109-116.

[9] LIU L G, ZHANG L, XU Y, et al. A local/global approach to mesh parameterization[J]. Computer Graphics Forum, 2008, 27(5): 1495-1504.

[10] LIU T T, BARGTEIL A W, O’BRIEN J F, et al. Fast simulation of mass-spring systems[J]. ACM Transactions on Graphics, 2013, 32(6): 214:1-214:7.

[11] SORKINE O, RABINOVICH M. Least-squares rigid motion using SVD[EB/OL]. [2020-03-29]. https://www.mendeley.com/catalogue/498963b1-7979-3736-915b-85ff25716ed4/.

[12] ANDERSON D G. Iterative procedures for nonlinear integral equations[J]. Journal of the ACM, 1965, 12(4): 547-560.

[13] PULAY P. Convergence acceleration of iterative sequences the case of SCF iteration[J]. Chemical Physics Letters, 1980, 73(2): 393-398.

[14] LIPNIKOV K, SVYATSKIY D, VASSILEVSKI Y. Anderson acceleration for nonlinear finite volume scheme for advection-diffusion problems[J]. SIAM Journal on Scientific Computing, 2013, 35(2): A1120-A1136.

[15] DE STERCK H. A nonlinear GMRES optimization algorithm for canonical tensor decomposition[J]. SIAM Journal on Scientific Computing, 2011, 34(3): A1351-A1379.

[16] PENG Y, DENG B L, ZHANG J Y, et al. Anderson acceleration for geometry optimization and physics simulation[J]. ACM Transactions on Graphics, 2018, 37(4): 1-14.

[17] FANG H R, SAAD Y. Two classes of multisecant methods for nonlinear acceleration[J]. Numerical Linear Algebra with Applications, 2009, 16(3): 197-221.

[18] TOTH A, ELLIS J A, EVANS T, et al. Local improvement results for Anderson acceleration with inaccurate function evaluations[J]. SIAM Journal on Scientific Computing, 2017, 39(5): S47-S65.

[19] HU S M, WALLNER J. A second order algorithm for orthogonal projection onto curves and surfaces[J]. Computer Aided Geometric Design, 2005, 22(3): 251-260.

Anderson acceleration for B-spline curve fitting

QIN Wen-jie, ZHANG Ju-yong

(School of Mathematical Sciences of University of Science and Technology of China, Hefei Anhui 230026, China)

In recent years, curve fitting technology has been widely used in image processing, engineering experiments and other fields. Among them, B-spline curve fitting is the most common method in curve fitting, the method of B-spline curve fitting has the advantages of locality, continuity but the fitting precision is relatively low. In practical application, B-spline curve fitting requires higher accuracy and speed. In order to increase the speed of planar B-spline curve fitting, Anderson acceleration is applied to the method of planar B-spline curve fitting. And then a quasi-Newton method based on Anderson acceleration is proposed. Firstly, an initial shape is set, and then the position parameters of the projection point of each data point are found according to the initial shape. Then, the corresponding position of control points is calculated by Anderson acceleration, and the above two steps are iterated until the result converges. The experimental results show that the proposed method in this paper outperforms other methods with respect to convergence speed and iteration time.

B-spline fitting; Anderson acceleration; quasi-Newton method; curve fitting; spline approach

TP 391

10.11996/JG.j.2095-302X.2020020246

A

2095-302X(2020)02-0246-08

2019-08-19；

2019-09-28

秦文杰(1994–)，男，江苏常州人，硕士研究生。主要研究方向为计算机图形学、最优化算法。E-mail：darkqin@mail.ustc.edu.cn

张举勇(1984–)，男，重庆人，副教授，博士。主要研究方向为计算机图形学、计算机视觉、数字图像处理、数值最优化。E-mail：juyong@ustc.edu.cn