基于LINGO软件的最短路线问题研究

丁正阳

目前，科技的发展越来越快，计算机和信息技术得到越来越广泛的发展。既然要发展，我们就要选择最优的方案，换句话说，也就是消耗资源最小的方案。这也是为了实现资源优化配置的一个主要途径。因此最短路线问题就显得尤为重要，它在交通运输、网络通讯、资源配置等方面有着极为广泛的应用。前人也对这个问题做了大量的研究。参考文献[1]对任意城市间的最短路径问题进行了研究，简单介绍了Dijkstra 算法和Floyd 算法，并且用用MATLAB 软件编写了一段简单的程序Floyd 算法进行了进一步的验证，证明了方法的正确性。参考文献[2]对动态规划的基本原理进行了介绍，并将动态规划成功运用到了运输问题的最短路径当中，结合实例对该方法进行了说明，并且阐述了动态规划整体最优思想和其在求解最短路径问题中的独特优越性。参考文献[3]对大城市的公共交通网络进行了分析，利用图论方法对观光旅游的乘车路径问题进行了设计规划，最后得到的结果能够进行进一步推广应用。

LINGO 软件具有十分强大的功能，可以通过内部已有的函数对0-1 整数规划问题进行求解，软件求解精度高，速度快，并且小巧方便。

1 建模

1.1 数学模型

最短路径问题旨在寻找图中节点与节点之间的最短路径，可以广泛应用到人工智能，神经网络，通信和计算机等学科当中，实际生活中的道路建设，电网铺设，路线规划等等问题也可以用最短路径问题进行描述。最短路径问题有多种类型，典型的任意一点到终点的最短路径问题描述如下。首先给定一张网络图，图中有点和线组成，或者线上还有方向箭头。所有的个点另为，组成集合，集合中的任意一点到另一点的距离我们用表示，假设到没有先进行连接，则令到的距离，并且当时，令，我们任意指定一个终点，求从点出发到的最短路线。

1.2 求解方法

首先介绍一种常用并且对于求解最短路径十分有效的方法—动态规划。动态规划法不是一种局部最优的思想，而是一种全局最优的思想。按照一定的次序求得每个阶段的结果，最终得到得到整个问题的最优化的解。

根据前人对该方法的总结，我们可以将动态规划法归纳为如下的表达式：

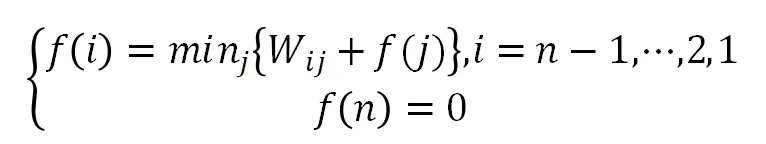
除了常用的动态规划法，我们也可以利用0-1整数规划法来求解最短路径问题。0-1 整数规划问题具有广泛的应用基础，比如线路设计、工厂选址等问题时，都可以采用0-1 变量即逻辑变量，建立数学模型，在满足条件的前提下，使目标解达到最优。应用0-1 整数规划模型求解最短路径问题的思路如下：

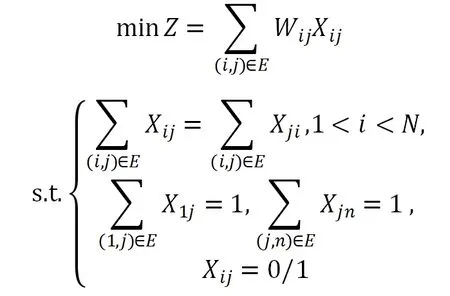
2 案例分析

2.1 案例

如图1 所示，A，B，C，D，E，F，G，H，K 表示9 个不同的村庄，村庄之间的连线表示两个村庄之间的距离，用表示。现在有一个居民需要从村庄A 到村庄K，请求出两村庄之间的最短路线。

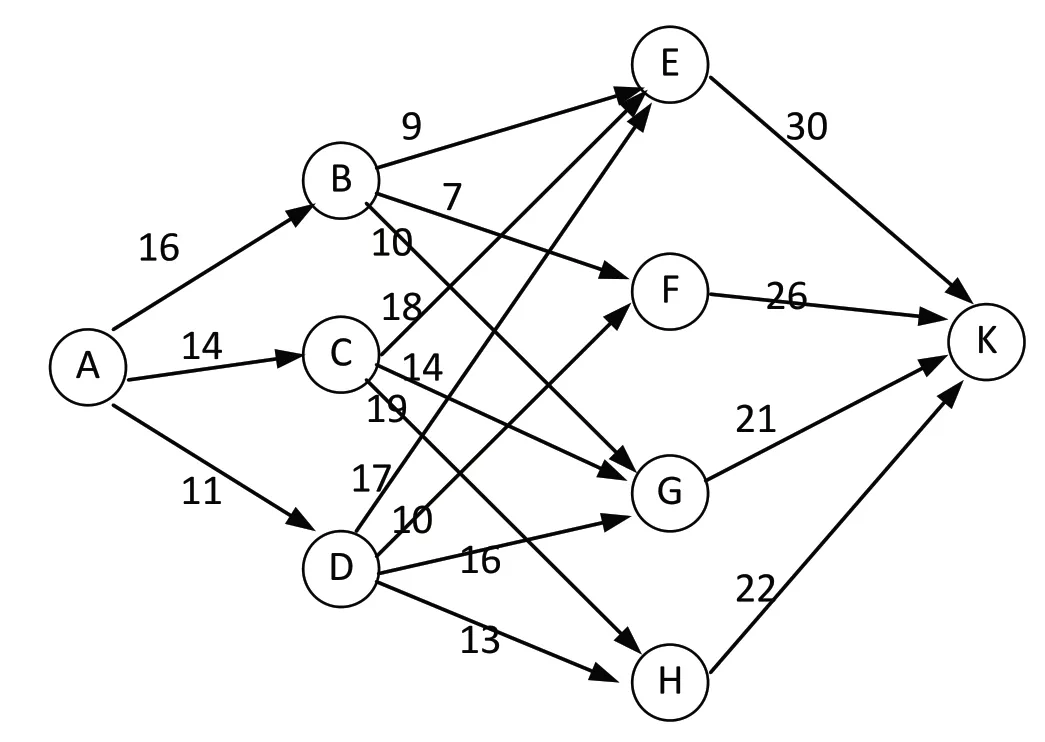
图1 9个村庄之间的网络图

动态规划法：

该问题有三个阶段，第一阶段从A 到B 或C 到D，第二阶段到E,F 或G 或H，第三阶段到终点K，我们从终点往前倒退。对于第三阶段：从集合E,F,G,H 到终点K 的路径分别为30,26,21,22，只有唯一的一条路，这就是最短路，标记为，，，；对于第二阶段：和集合E,F,G,H 相连的下一个阶段的集合是B,C,D，则从B 出发到E,F,G，再到终点K 的路程长度是：

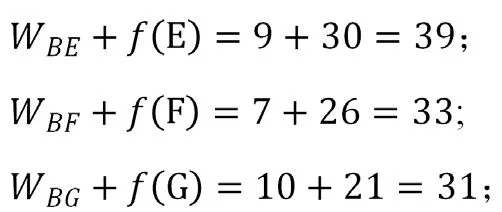
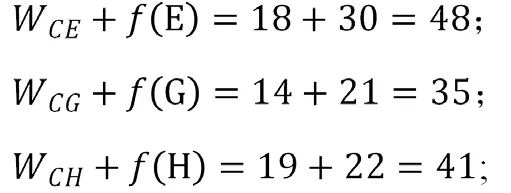
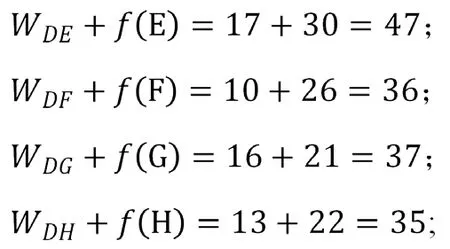
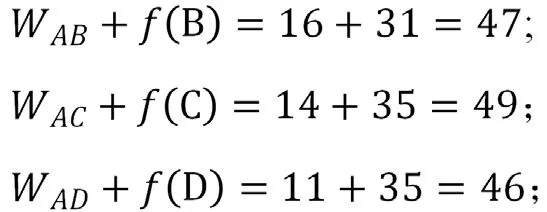
0-1 整数规划法：

由于0-1 整数规划模型在最短路中的算法是遍历进行试凑，因此对于数据点一旦上升的情况没有实用性，因此不采用人工手动求解的方式进行演示，将直接通过计算机编程进行求解。

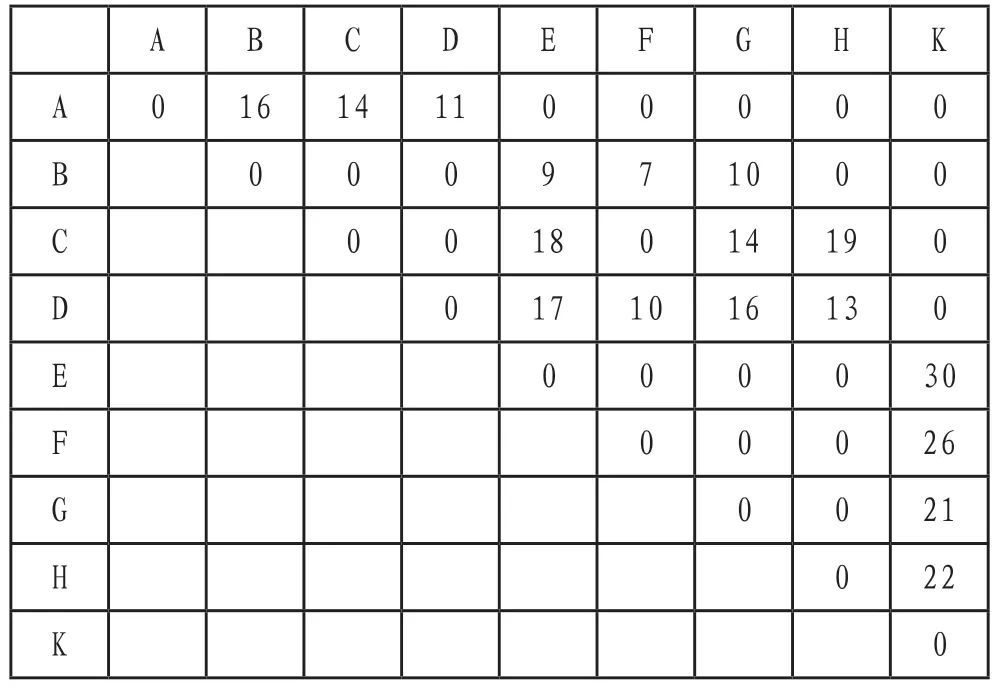
表1 0-1整数规划法求解最短路径

利用0-1 整数规划法进行最短路径问题的手工计算主要是采用整数规划的方法，按照约束条件对所有可能路径进行0-1 试凑，求出某一目标函数值，并且对所有的可能的路径组合的目标函数值进行比较，见表1。

2.2 求解过程

LINGO 软件的程序：

1）动态规划程序

得到的结果如表2 所示：

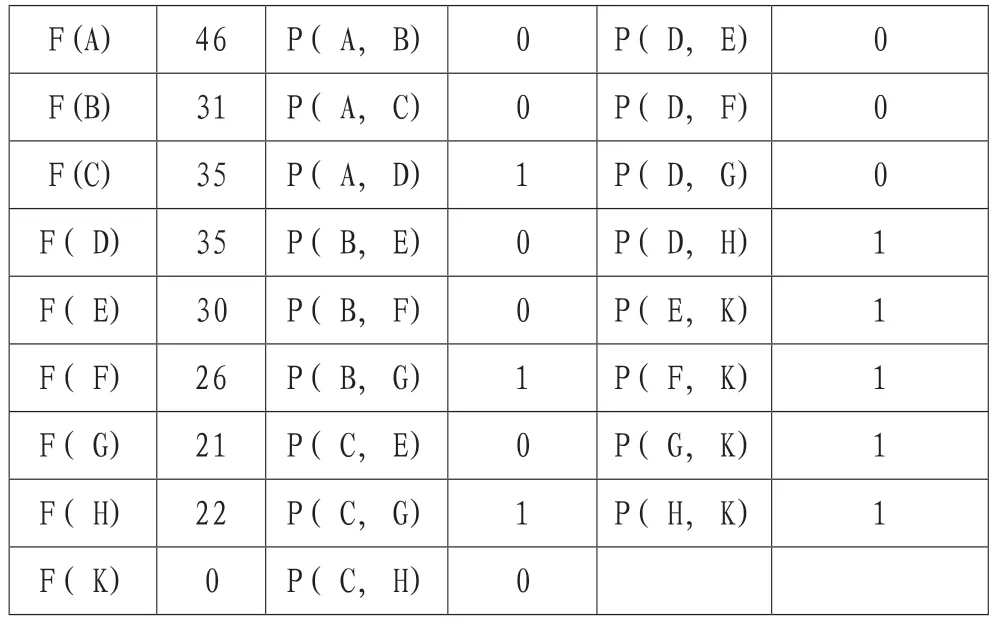
表2 动态规划法求得结果

其中P(H,K)=1 就是最短路径经过这条弧的意思；P(D,G)=0 就是最短路径不经过这条弧的意思；因为P(A,D)=1，P(D,H)=1，P(H,K)=1，所以从A 点到K 点的最短路径是从A 点经过D 点到H 点最后再到K 点。

2）0-1 整数规划程序

得到的结果如下（见表3）：

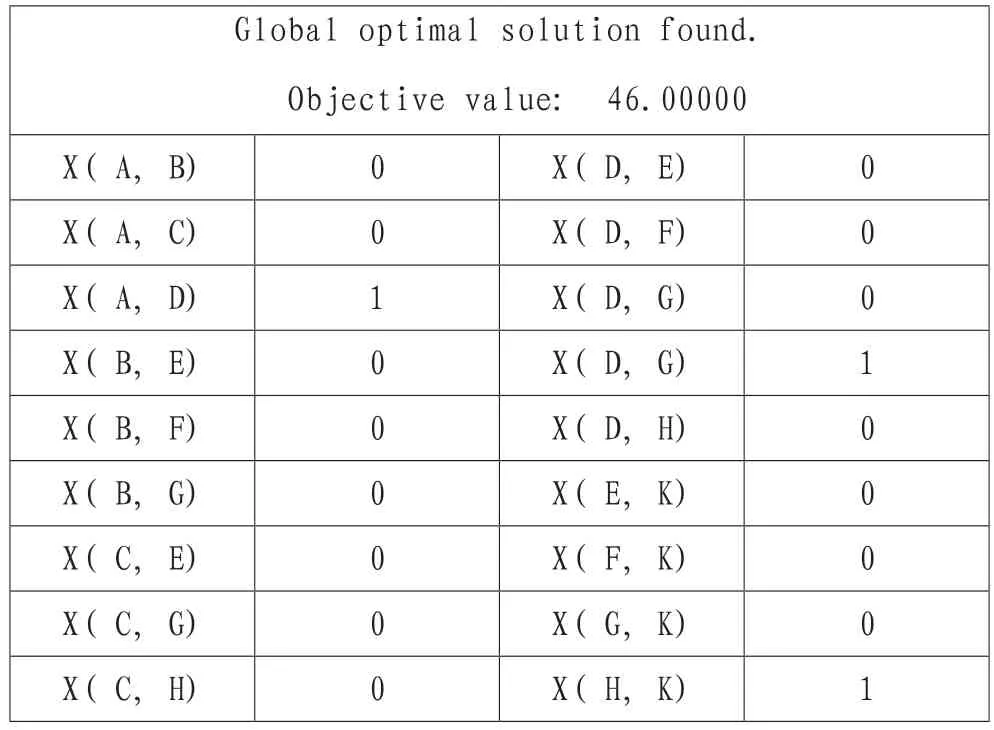
表3 0-1整数规划法求得结果

其中X(A,D)=1 表示从村庄A 到村庄K 的最短路径经过了D 点，X(i,j)=0 表示从村庄A 到村庄K的最短路径没有经过某点或某条路径。从表3 可知最短路径为A-D-G-K，总的长度为46。

3 结论

本文讲解了动态规划法和0-1 整数规划法以及LINGO 软件对求解最短路径问题的作用。同样的经过对文章中的案例和生活中其他案例的分析计算，本文所采用的方法具有普适性。可以解决诸如物流配送、道路建设、网络铺设等一系列问题，除此之外当然也要考虑人力资源配置和当地造价等一系列其他的因素。