基于流固耦合的管道机器人清淤装置

罗继曼，印 辉，郭松涛,戴璐璐

(沈阳建筑大学 机械工程学院，沈阳 110168)

清淤装置作为管道清淤机器人的核心装置，其清淤能力和清淤效果是评价该装置设计合理性的重要指标。使用机械化装置对排污管道进行清淤过程中，因清淤装置的几何复杂性，以及管道内流体、固体及气体等介质的未知的相互作用，使得实际的清淤过程产生了复杂的流固耦合效应[1]。

目前，中外对清淤装置的研究很少，而在流固耦合研究中大多对固体装置在流体中的模态、强度或者力学特性进行研究。吴晓茹等[2]对悬浮式液压立柱进行静力学和单向流固耦合分析，研究其在不同载荷工况下的应力和变形情况，保证液压立柱具有良好的强度和工作性能。隋秀华等[3]从单向流固耦合方向对缸体结构进行分析，分析该缸体的应力和变形，确定缸体的危险位置。前人对流固耦合研究多是通过流体作用后对结构进行相应分析，缺少结构对流体作用的深入研究。研究结构作用于流体后流体的运动状态是验证清淤装置的清淤能力的有效直观的方法。

基于此，利用有限元方法对管道机器人清淤装置在管道中进行流固耦合研究，得到清淤装置与流体相互作用后的流体运动状态，以验证其清淤能力，为该装置的控制系统的研究提供理论依据。

1 清淤装置模型

1.1 清淤机器人模型

以大管径的管道机器人为研究对象，设计研发出一种新型管道清淤机器人。新型管道清淤机器人的工作环境为直径800～1 000 mm，纵深长度小于90 m的地下排水管道。考虑到管道形状和尺寸，机器人体积尽可能地小，考虑到排水管道形状多为圆形，因此机器人外形采用圆柱体结构设计，其机械系统主要由三部分组成，分别为轮式行走机构、步进机构和清淤机构，如图1所示。清淤机构是管道清淤机器人清除管道淤泥的核心部件由支撑装置、清淤盘和叶片组成，如图2所示。

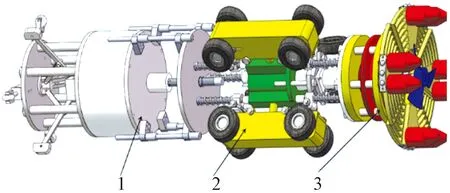
1为步进机构；2为轮式行走机构；3为清淤机构图1 管道清淤器人整机结构Fig.1 The picture of robot structure

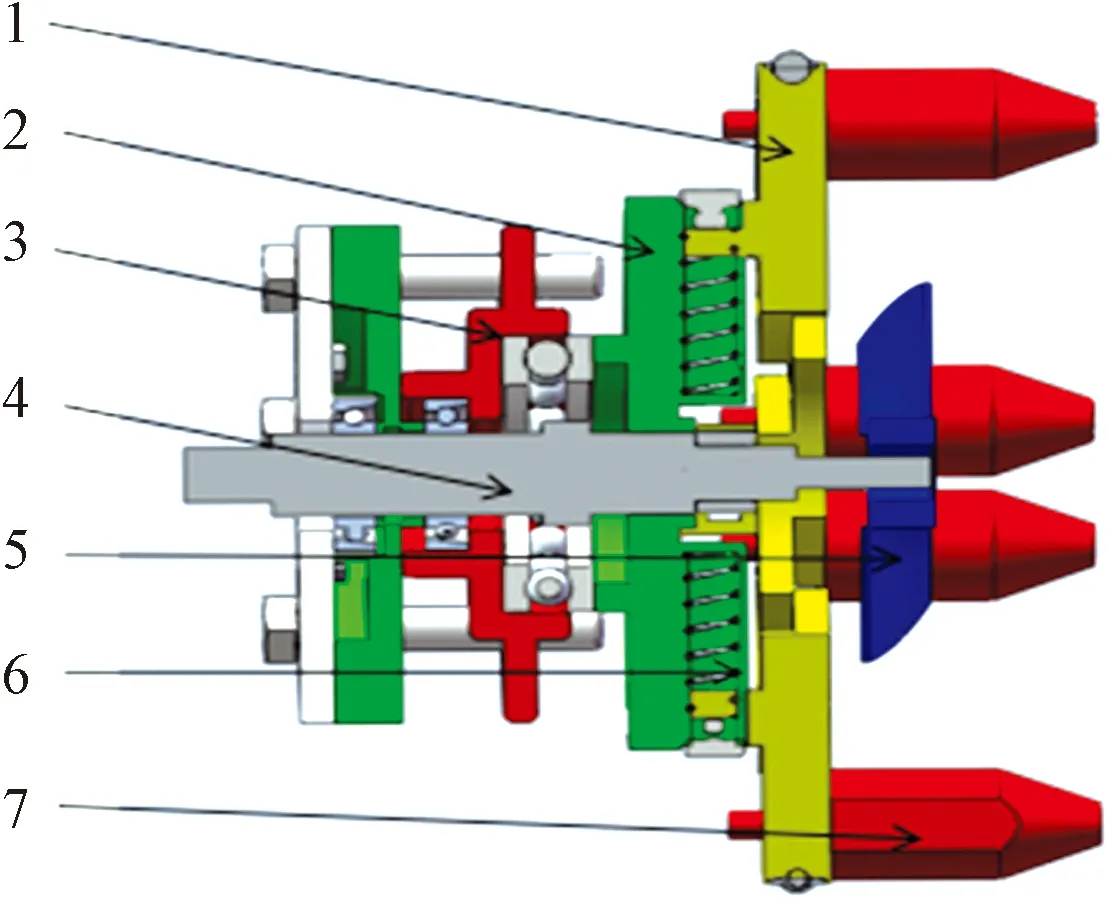
1为扇形盘；2为连接盘；3为支撑盘；4为主轴；5为叶片；6为弹簧；7为刮刀图2 清淤装置剖视图Fig.2 The sectional view of dredging device

1.2 工作原理

在推进系统和主轴旋转时实现刮削-搅拌-过滤-推进-自流冲刷的五位一体清淤动作。扇形盘通过弹簧和滑道的作用可实现在管道内的过载保护功能，在清淤装置的动力特性研究中得到扇形盘在滑道内的振动幅度很小，对流体的影响很小，即在流固耦合分析时不考虑扇形盘的振动。

1.3 确定运动参数

确定清淤运动转速与推进速度,在运动学分析中，分析污泥的流变特性得出以下结论。如图3所示，当清淤盘旋转速度达到0.3～1.6 r/s时，污泥的黏度下降率可达到90%以上，并逐渐趋于稳定即达到极限黏度[4]，依据这一结论，确定了清淤盘的转速为0.3～1.6 r/s。通过查阅城市排污管道相关资料[5]，设定清淤工况，参数如表1所示。机器人在管道内清淤时，前进的阻力主要来自污水流动的作用，根据表1所示的污水流速，考虑顺流时阻力为0的理想状态，确定清淤装置前进方向的速度为0.5～2.5 m/s。

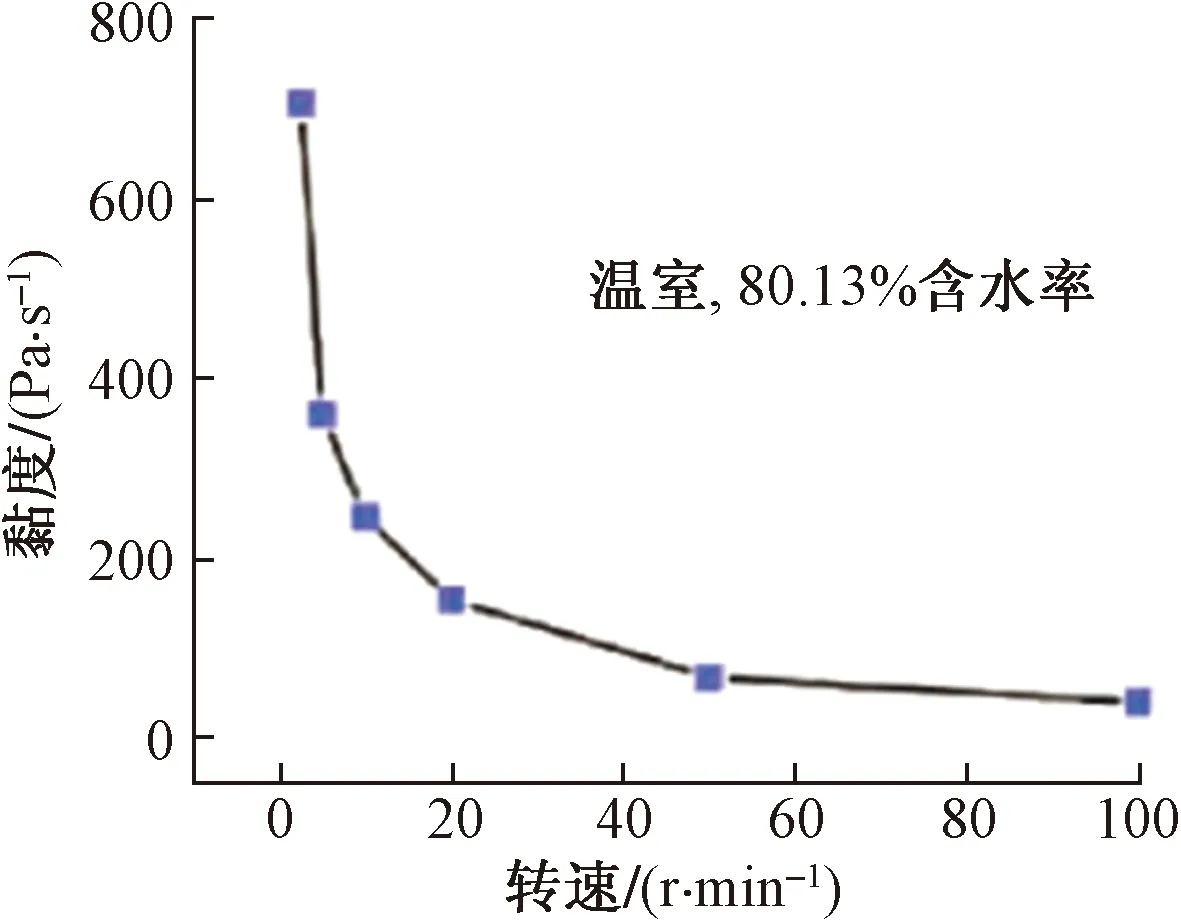
图3 污泥流变特性曲线Fig.3 The curve of sludge rheology characteristic

表1 清淤装置的工况参数Table 1 Working condition of dredging device

2 流固耦合分析

固体和液体之间的相互作用是流固耦合力学的重要特征，即：在流体载荷作用下固体会产生相应的变形或运动，同样变形或运动又会对液体流场产生影响，改变该流体载荷的分布和大小。在这种相互作用和不同条件下产生了形形色色的流固耦合现象[6]。

2.1 流固模型处理

将简化后的清淤装置模型导入ANSYS Workbench软件中，并通过Geometry工具为其添加流体域，并进行布尔减运算处理流固域重叠部分，将处理过的流固模型导入到mesh模块，由于清淤装置结构不规整，而流体域和部分结构形状规则，所以采取MultiZone网格划分方法，采取系统默认的识别方法自动划分合适的网格。

图4 流体域有限元模型Fig.4 Fluid domain finite element model

2.2 有限元模型

模型基于流体域的网格划分如图4所示，其中有458 858个单元，共计127 468个节点。该模型基于固体域的网格划分如图5所示，有270 423单元，共计57 588个节点。由于计算机计算能力有限，网格划分将流固耦合交界面处划分的较细，而距离耦合面处比较远的流体域处划分的较大，这样可以在不影响精度的前提下节省计算时间。

图5 固体域有限元模型Fig.5 Solid domain finite element model

3 流固耦合的有限元法

3.1 流固耦合方程

流固耦合分析常采用分离解法[7]。分离解法又称载荷传递法，是为研究清淤装置对流体的作用采取固-流单向耦合仿真方法，即采用数据由固体传递到流体的传递路径。结构对流体的作用体现在流体的压力和速度的改变，因此用速度和压力来描述流体运动[8]。

3.1.1 压力场下的流体运动方程

设污泥流体为均匀不可压缩介质，可得流体动力平衡方程为

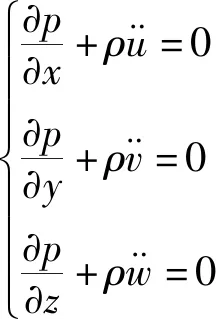
(1)

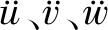
在流体连续下条件下[式(2)]得到基于压力场表达的流体运动方程[式(3)]。

(2)

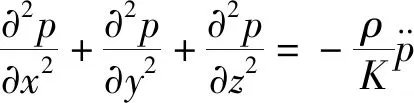
(3)

3.1.2 速度场下的流体运动方程

存在以速度势φ(x,y,z,t)与速度分量得到流体动平衡方程为

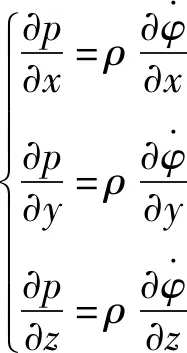
(4)

在流体连续条件[式(5)]下得到速度势的流体运动方程[式(6)]。

(5)

(6)

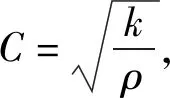
3.1.3 结构运动方程

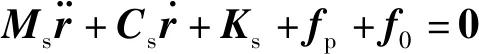
(7)

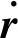
3.1.4 耦合面的数据传递

基于流固耦合分析的数据传递路径是通过接触面将流体计算结果和固体计算结果相互交换传递[9]，如图4所示。在耦合接触面处，该清淤装置的位移变量可以传递给流体，流体的应力变量也可以传递给清淤装置，但基于流固耦合分析的速度参数不能传递到固体耦合面上，同样固体耦合面上应力分布也无法传递到流体场中[10]。

3.2 流固耦合参数设置

进入CFX(computational fluid X)模块，根据表1所示的工况参数，由于计算能力有限设置流体域长度为1 000 mm，流体域直径为320 mm，污水流速为2.5 m/s，密度为2 600 kg/m3，出口压力为0。对给排水管道进行水利计算时，管道内流体流态均按湍流考虑，湍流模型设置为K-epsilon，动力黏度为0.01 Pa·s。

为验证清淤能力，清淤能力仿真采取固-流单向耦合设置计算。根据1.3节清淤装置转速、前进方向速度以及流体流速，考虑顺流和逆流的实际工况，并在逆流条件下在最低转速和最高转速时，在顺流条件下考虑无阻力时，计算清淤装置对流体的耦合作用，仿真初始条件如表2所示。

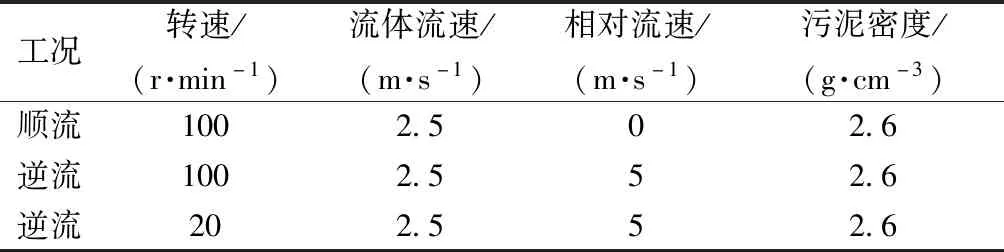
表2 仿真参数Table 2 Simulation parameter

3.3 流固耦合后处理

设置收敛精度为0.001，耦合迭代曲线在计算到700步时各参数收敛。考虑真实工况下的重力作用，流固耦合后处理时选取Y方向的管道中间界面提取仿真示意图。逆流高转速时，基于速度和压力的流体运动曲线如图6所示；逆流低转速时，基于速度和压力的流体运动曲线如图7所示；顺流高转速时，基于速度和压力的流体运动曲线如图8所示。仿真分析结果如表3所示。

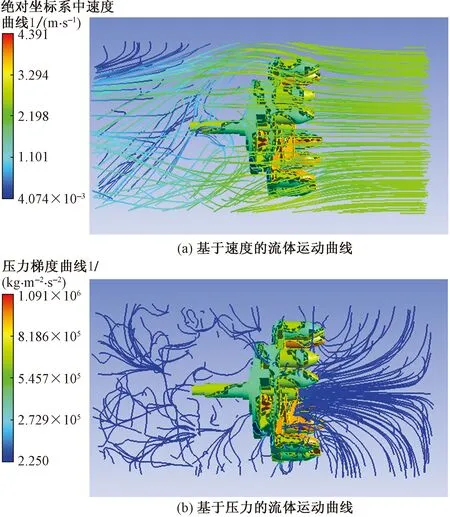
图6 逆流高转速Fig.6 Countercurrent and high speed

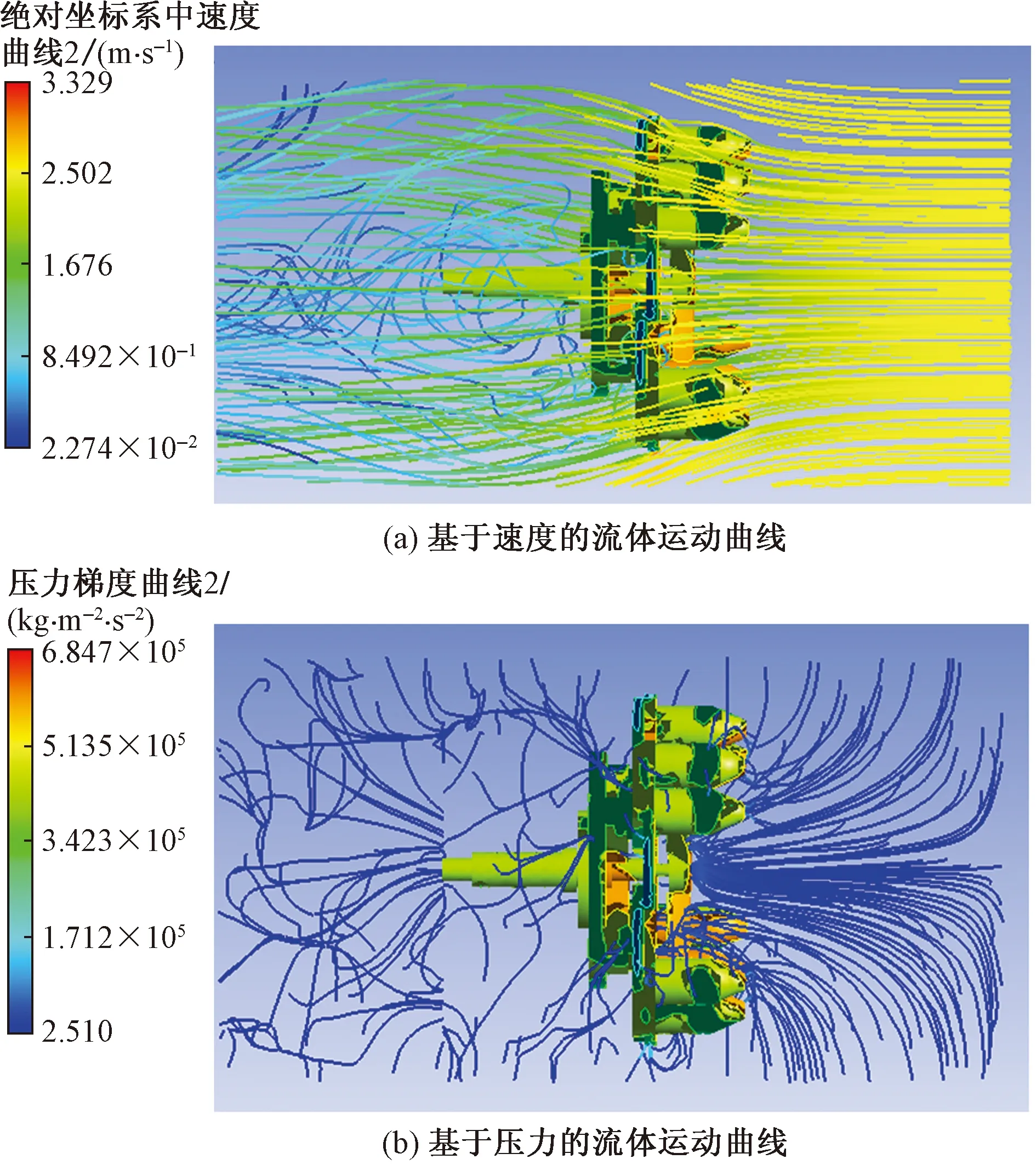
图7 逆流低转速Fig.7 Downstream and down speed

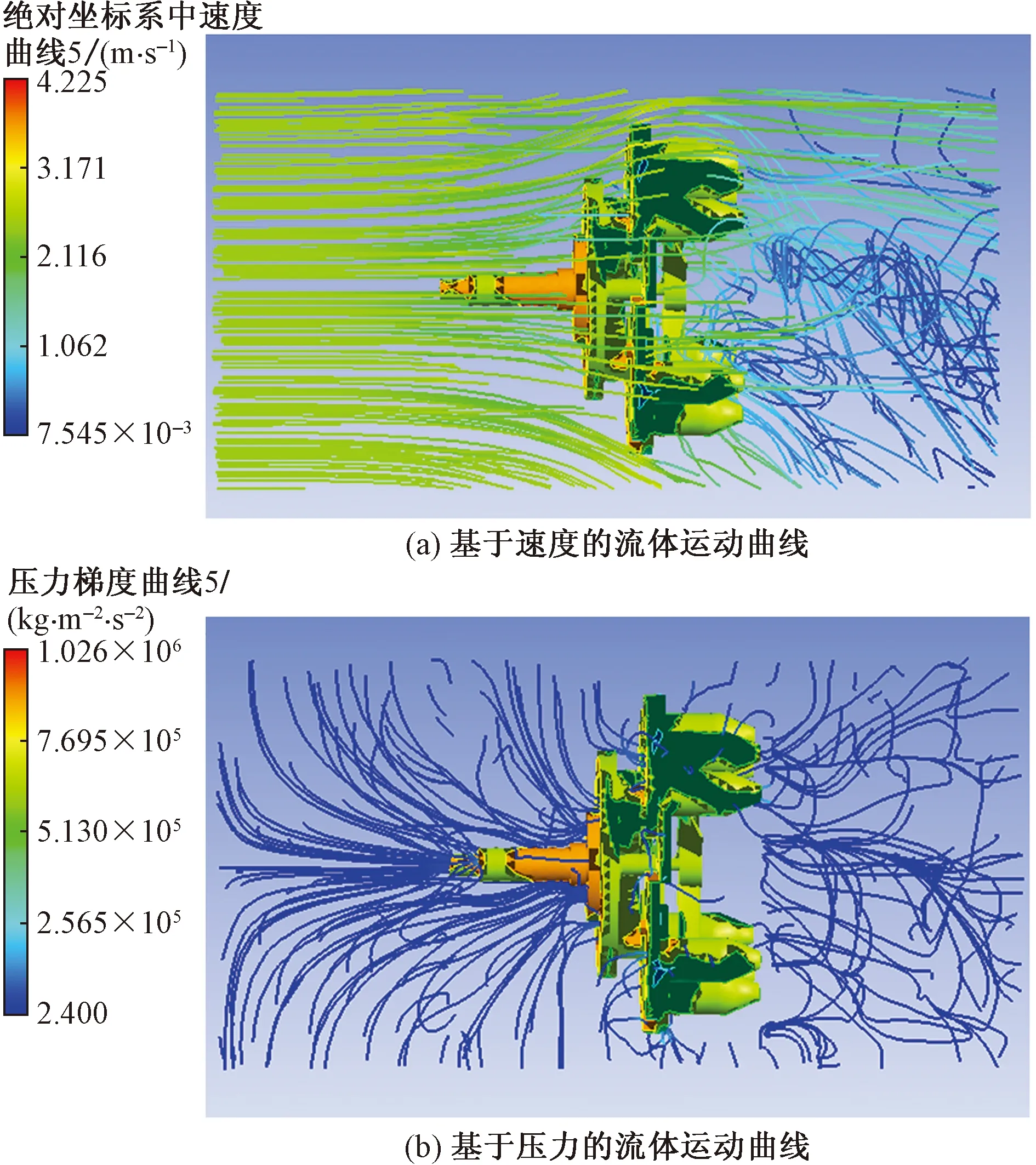
图8 顺流高转速Fig.8 Downstream and high speed

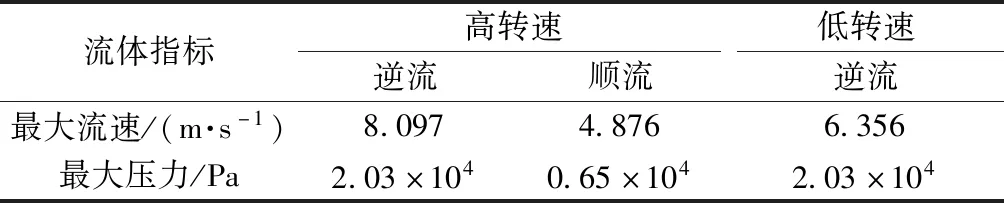
表3 仿真分析结果Table 3 Analysis result of simulation

分析图6～图8、表3可知：①逆流条件下，高转速(100 r/min)与低转速(20 r/min)时，结构对流体产生的压力相同，高转速相对低转速情况下结构对流体作用的速度提高了27.4%，高转速是低转速的5倍，故转速对流体运动速度的提高效率比较低；②在高转速条件下，逆流流速相对顺流流速提高66.1%，逆流流体压力相对顺流流体压力提高210.6%；③对比图6与图7可知，逆流高转速相对逆流低转速，流体的紊流状态范围更大、更显著，而逆流低转速时，流体的紊流状态只发生在清淤装置的中后部；④对比图6和图8可知，高转速时，流体运动均在旋转域内发生滞后于清淤装置的旋流，而逆流相对于顺流时，清淤装置前后的流体的紊流状态更显著。

4 结论

对清淤装置进行了旋转条件下的流固单向耦合研究，得到以下结论。

(1)流体最大速度与最大应力均发生在清淤装置与流体接触面处，以及清淤装置的旋转域内，清淤装置在逆流高转速条件下对流体的搅拌作用效果显著，有利于将沉积在管道内壁底部的淤泥搅拌并细化成推移质状态。

(2)通过清淤装置的流体会发生剧烈不规则运动，有利于淤泥的离散化；高转下的搅拌效果更好，逆流条件下清淤装置对流体作用的速度与压力更大，对淤泥的清淤效果更好。