基于相对灵敏度分析的高速列车车体结构优化
石晓飞, 唐 晖, 高月华
(1 中国铁路广州局集团有限公司, 广州 511483;2 大连交通大学 交通运输工程学院, 辽宁大连 116028)
高速列车车体主要是由地板、侧墙、车顶和端墙等部分焊接而成的薄壁筒形整体承载结构。整备状态下的车体一阶垂弯频率是反映车体振动性能好坏的重要参数。一阶垂弯频率较低表明车体刚度偏软,不仅会降低列车在运行中的乘坐舒适度,还很有可能致使车体因振动过大而导致局部产生较大变形,影响材料疲劳寿命,从而影响列车运行稳定性,无法最大程度的发挥车体承载结构的承载能力。随着列车运营速度的提升,列车阻力及作用力急剧增大,线路固有频率范围增大,使得车体振动情况以及旅客舒适度也进一步恶化。为了避免或减少此类情况的发生,需要对车体承载结构进行合理的优化设计,提高整备状态下车体的一阶垂弯频率,这样不仅可以有效的避免与转向架构架的自振频率产生共振,还可以减小车体的振动,改善其乘坐舒适度及运行平稳性。
在保证车体质量在变化幅度不大的同时,最大程度的提高车体的一阶垂弯频率是国内外学者研究的热点。Enblom等[1]在考虑了振动舒适度、车辆动力学性能及车体强度的基础上对车辆舒适度进行了静强度分析和多体动力学的两级协同优化。干宇文和张立民[2]以内侧地板、侧墙和车顶作为研究对象,分析了承载结构厚度尺寸的变化对车体一阶垂向弯曲、菱形和扭转变形固有频率的影响。结果表明,车顶厚度的变化对车体模态频率的影响最大。崔嵩等[3]介绍了改善车体动态特性,提高一阶垂向弯曲振动频率的几种可行途径,如灵敏度分析,拓扑优化,改变结构阻尼,采用高阻尼金属、智能材料等。贾尚帅和韩铁礼[4]利用灵敏度分析方法,选取18个车体可调整的构件的厚度值作为设计变量,以整备车体的一阶垂向弯曲频率作为优化目标,对车体进行优化设计,优化后一阶垂弯频率有明显的提升。赵阳阳和刘士煜[5]通过调整车体侧墙高度、车窗位置和边梁厚度使车体模态频率达到最大值。李伟等[6]提出一种尺寸敏度分析方法改善车辆动态特性,应用ANSYS计算车体自由模态频率并提取振型,研究单一部件尺寸敏度对车体主振型模态频率的影响。
高速列车车体结构复杂,构件较多,如果在优化过程中盲目地考虑较多的设计参数,不仅对模型的优化求解增加困难,而且还会影响优化求解的精度,因此确定有效的设计参数极为重要。车体模态频率灵敏度分析可以使设计人员能够比较客观地了解车体固有频率对各个设计变量改变的响应情况,确定对结构响应最敏感的设计变量,从而提出合理的优化模型,有效改进高速列车的动态特性。通过相对灵敏度分析方法确定有效的设计变量,在保证车体质量变化较小的前提下,对车体结构进行优化设计以提高车体的一阶垂弯频率。
1 车体结构的有限元分析
车体采用中空挤压铝合金材料,整备质量39 t。经过合理的几何简化处理后,车体结构在左右方向上基本对称,前后方向上不对称。利用Hypermesh软件建立整车车体有限元模型如图1所示。

图1 铝合金车体有限元模型
为验证车体的结构性能是否满足相关标准的要求,对车体进行了静强度、刚度及模态的分析计算。在车体静强度分析的多种工况中,一般情况下最大垂向载荷状态下车钩缓冲区纵向1 500 kN压缩载荷的组合工况是高速列车在运行时所经受的最恶劣工况[7]。因此文中选择该组合工况对车体进行静强度校核,分析结果显示车体最大Von. Mises应力发生在上门角位置,其值为205 MPa,小于该处型材的许用应力225 MPa。在定员工况(垂向载荷449.50 kN)条件下,位于车体中心线底架边梁的最大垂向位移为7.06 mm,小于设计许用值17.80 mm,车体相当弯曲刚度2.51×109N·m2,大于设计许用值1.80×109N·m2。在扭转载荷工况(扭矩40 kN·m)作用下,车体相当扭转刚度7.99×108N·m2/rad,大于设计许用值5.5×108N·m2/rad。综上,车体的静态强度、刚度满足相关标准要求。
车体在整备状态下的前两阶主要振型的固有频率见表1,振型图分别如图2和图3所示。根据我国对于车体垂向弹性振动频率的规定,要求车体在整备状态下的一阶垂向弯曲振动频率不得小于10 Hz。车体在整备状态下的一阶垂弯频率为10.56 Hz,虽然数值大于标准要求,但仍较小。

表1 整备状态下模态计算结果

图2 车体一阶垂弯振型
2 车体结构灵敏度分析
2.1 灵敏度基本理论
灵敏度即求导信息,是一种度量,是一种评价由于设计变量或参数的改变而引起结构变化的变化程度的方法。模态频率灵敏度即结构自由振动频率对结构参数的灵敏度。模态频率灵敏度可以直接用结构的模态方程对设计变量进行微分得到。

图3 车体菱形振型
无阻尼结构特征方程为
([K]-λi[M]){φi}=0
(1)
式中[K]、[M]分别为结构刚度矩阵和结构质量矩阵;λi为结构第i个特征值,{φi}为结构第i个模态向量。
设第j个设计变量为xj,式(1)对其求导数得
(2)
由式 (1)得下式
(3)
式(2)左乘{φi}T,并结合式(3)可得模态频率灵敏度为
(4)

2.2 灵敏度分析
基于车体的静、动态特性的有限元分析结果,选取车顶、上边梁、侧墙及底板等车体主要型材的47个结构件计算车体模态频率和质量对构件厚度变化的敏感程度。构件信息见表2,车体一阶垂弯频率灵敏度和质量灵敏度的曲线图分别如图4、图5所示。
由灵敏度分析结果,不同部位的型材厚度对车体质量和一阶垂弯频率的灵敏度不同。由图4、图5可知,车体一阶垂弯频率的灵敏度数值有正、负之分,而车体质量灵敏度全是正值。正值表示型材厚度与车体一阶模态频率和质量有相同的变化趋势,负值则相反。单纯的依靠一阶垂弯频率灵敏度和质量灵敏度分析结果,仍旧很难选取有效的设计变量,比如底板加强筋(34)的两个灵敏度值都比较大,增加其厚度,虽然可以提高车体一阶垂弯频率,但同时也会引起车体质量的较大幅度的提高。为了能够更好地反映改变车体主要型材厚度对车体质量和一阶垂弯频率的影响,用相对灵敏度MTF表示一阶垂弯的灵敏度FS与质量灵敏度MS的比值,即MTF=FS/MS[8]。因为车身质量灵敏度全部为正值,而一阶垂弯频率灵敏度值则有正、负之分,所以相对灵敏度值也有正、负之分,如图6所示。

表2 构件厚度参数表 mm
根据相对灵敏度结果,将车体型材变量分为3类。第1类型材5、11、13、14、15、17、18、19、20、27、28、29、30、31、33、35的MTF值较大,对于一阶垂弯频率的提高有较为明显的作用;第2类型材1、2、3、4、6、7、10、12、16、21、22、23、24、25、26、32、34、36、37、38、39、40、41、42、43 的MTF值相对较小,型材厚度的增加对于车体一阶垂弯频率的提高影响很小,反而对质量的增加有更为显著的影响;第3类型材8、9、44、45、46、47的MTF为负值,减小型材的厚度不但会提高车体的一阶垂弯频率,还可以有效的减轻车体质量。综合上述相对灵敏度分析结果,对于车体的结构优化,第1类型材(车体的圆顶内外蒙皮,侧墙的内外蒙皮,上边梁外蒙皮,底板的内外蒙皮及筋板)和第3类型材(端墙内外蒙皮)能够保证车体质量变化较小的同时有效地提高车体的一阶垂弯频率。

图4 车体一阶垂弯灵敏度
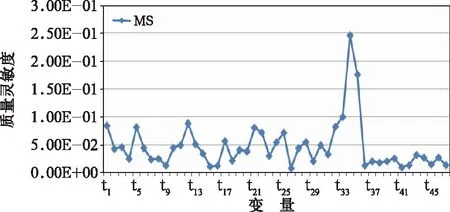
图5 车体质量灵敏度

图6 一阶垂弯相对灵敏度
3 车体结构优化设计
3.1 优化设计模型
根据相对灵敏度分析结果,确定第1类和第3类型材的厚度作为设计变量,变化范围为初始厚度的30%(见表3)。考虑到车体的轻量化,综合考虑车体质量和一阶垂弯频率的作用关系,车体在优化过程中质量不能有明显的增加,选取车体铝合金结构总质量增重不大于2%作为约束条件。以车体一阶垂弯频率最大化为目标函数,构建车体结构优化模型。具体优化模型如下:
(5)
式(5)中X为设计变量向量,xi为第i个设计变量,设计变量要满足上下限xU,xL的要求(见表3);目标函数Λ1为车体一阶垂弯频率;M为车体铝合金结构质量,M0为车体铝合金结构初始质量。
3.2 优化结果及分析
基于给定的优化模型,应用建立近似显示模型的方法进行车体结构优化设计,经过3次迭代后优化过程结束,其目标函数的迭代曲线如图7所示。车体一阶垂弯频率随迭代步数的增加逐渐增加,优化前车体一阶垂弯频率为10.56 Hz,优化后车体一阶垂弯频率为11.14 Hz,频率提高了5.5%,车体动态刚度得到有效提高。另外车体的二阶菱形振动频率提高为12.35 Hz,较优化前提高了3.1%。优化后的车体铝合金结构质量增重1.7%,符合预期目的。
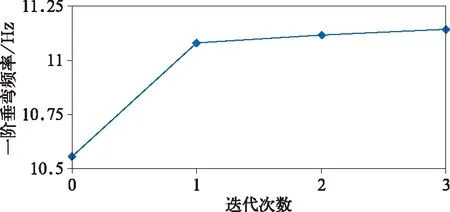
图7 优化迭代过程
设计变量的优化结果见表3。由表3中数据可知,圆顶、上边梁、侧墙型材处的设计变量取上限值;平顶、端墙型材处的设计变量取下限值;底板及下边梁型材处的设计变量取中间值。由于在优化过程中设计变量的厚度变化是连续的,优化结果中一些构件的厚度不可避
免会出现多位小数,不能直接用于实际生产,因此对优化结果进行圆整,具体调整值见表3。
对优化后的车体结构进行了静态刚度及强度校核,结果见表4。由表4中的对比数据可知,优化后车体的刚度及强度均有了不同程度的提高,符合相关标准的规定。

表3 设计变量参数表 mm

表4 车体优化前后主要性能指标对比
4 结 论
以车体结构的静、动态特性的有限元计算为基础,对车体结构进行了动态灵敏度分析,并基于灵敏度分析结果对车体进行了结构优化设计。
(1) 车体结构的模态分析结果表明:车体的一阶垂弯频率略大于相关标准规定,其数值较小。
(2)灵敏度分析结果显示:车体的圆顶内蒙皮、平顶筋板、侧墙内外蒙皮、底板的内外蒙皮、上边梁内外蒙皮和端墙等车体的型材结构对一阶垂弯频率影响较大,对质量的变化影响较小。
(3) 经灵敏度分析确定有效的设计变量,针对性地对车体结构进行尺寸优化,优化后的车体一阶垂弯频率提高5.5%,车体铝合金结构增重1.7%,达到优化的预期目的。
(4)优化后的车体结构的静强度、刚度等方面均有不同程度的提高。

