挖掘图形特征 凸显问题本质
施平
[摘 要] 试题命制源于教材,以课本资源为载体,从学生已有的活动经验出发,关注提升数学核心素养;试题的命制过程,是经历从原始框架到几易其稿,再到最终定稿的蜕变过程;依托图形的性质进行深层次的挖掘拓展延伸,揭示问题的本质特征.
[关键词] 试题;命制;生成;思考;延伸
笔者有幸多次参与本县市统一考试数学试题命题工作,在试题的命制过程中逐步掌握一些命题技术、原则和技巧;对于本道题的命制,基于图形的基本特征,借助“几何画板”的动态与度量功能,持续挖掘,不断增强试题与预设目标的契合度,经历了反复权衡、不断斟酌、抽丝剥茧、凸显内涵的过程. 以下笔者将对试题如何生成、命题过程中的思考以及试题拓展延伸讲一些体会,与同行交流.
试题展示
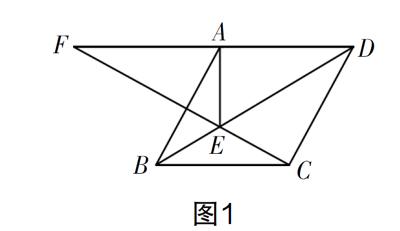
如图1,菱形ABCD中,AB=4,∠ABC=α(0<α≤90°),E为BD上的一个动点(不与B重合),BE (1)求证:∠AFE=∠BAE. (2)若α=60°, ①当△AEF为直角三角形时,求BE的长; ②点M为BE的中点,求CE+ME的最小值. 命题立意及来源 (一)命题立意 本试题的命制,借助几何基本图形的特征,将导角问题、特殊三角形存在探究问题、最值问题、相似、圆等有机融合一起,力求既能深度考查初中数学的核心知识,又能综合考查数学基本思想方法的运用;既能提升学生数学核心素养,又能挖掘学生后续的数学学习能力. 知识层面:着重考查平行线的性质、全等三角形的性质判定、角平分线性质、菱形的性质、直角三角形的性质、勾股定理、三角形三边关系、垂线段最短等; 思想层面:试题渗透转化、数形结合、分类讨论、方程函数、特殊与一般的思想; 能力层面:力求提高抽象概括能力、推理论证能力、运算求解能力和创新意識; 素养层面:关注提升学生的逻辑推理、直观想象、数学运算等核心素养. (二)原始模型 命制时选取的素材是人教版八年级下册第十八章56页的例3,通过这个例题给我们启示:赋予菱形一个内角度数和边长,即可求出其他的元素,包括其他边、其他角、两对角线长,菱形的高、周长、面积等. 试题的生成与解析 菱形是特殊的平行四边形,具有平行四边形所有的性质,同时菱形又有一个很重要的本质特征——对称性. 基于此,本道试题就以菱形为基本图形,通过菱形的对角线特征(垂直平分、平分对角),利用菱形的对称性,如图2在对角线BD(对称轴)上任取一点E,设置BE 1. 点E在运动时,∠AFE在变化,但由于平行关系,∠AFE恒等于∠FCB,而∠FCB=∠BAE,导角得出角之间的相等关系,基于此思考,第一问设置了一个两角相等的证明问题. 2. 赋予∠ABC=60° ,几何画板上拖动E点,在运动变化过程中观察△AEF,其特征是点A定,点E和点F在动,在某个位置可能出现特殊三角形,进而可以设置三角形的存在探究型问题,而特殊三角形的指向可能是直角或等腰三角形,引发学生分情况讨论直角三角形存在的可能性. 图形定性后考查线段或角度的定量,探究直角三角形下边角之间的特殊关系,可直接计算或通过设元利用勾股定理将问题转化,实现从定性到定量的有效融合,通过由静到动的过程拓宽试题的广度,设置存在探究性问题达到思维路径和解决策略的开放性. 3. 菱形中的最值问题常围绕“菱形的高”去命制,本问对高进行拆分,看成由两线段AE和EH构成,AE通过对称可转化为CE,EH可利用直角三角形30度的特殊边角关系与ME进行互化,并利用菱形的对称性、两点之间线段最短(三角形三边关系)或垂线段最短将两线段最值问题转化为单线段(即菱形的高)最值问题. 试题的拓展延伸 在命完上述问题后,仔细琢磨这个图形,借助画板继续挖掘图形特征,笔者尝试在原题基础上做变化拓展延伸. 1. 延伸1:对于原题的第一问(求证两角相等),结合一个公共角相等,可进一步发现△AEG∽△FEA,即由此可拓展延伸为:求证AE2=EG·EF,或由于对称性得到AE=EC,可设置问题“探索EC,EG,EF三条线段的数量关系,并说明理由”. 2. 延伸2:原题的第二问设置了直角三角形的存在探究类问题,尝试拓展为:当△AEF为等腰三角形时,求BE的长. 这里同样需要分情况讨论. 简解 (1)若FA=FE,如图5,可求得∠F=20°,进而得出∠EAO=40°,并将BE转化,进而可求出BE=OB-OE=2 -2 tan40°; (2)若AE=AF,如图6,可求得∠F=40°,进而得出∠EAO=20°,并将BE转化,即可求出BE=OB-OE=2 -2tan20°; (3)若EA=EF,出现∠EFA=∠FAE=∠BAE的情况,即∠FAB=0°,与已知产生矛盾,故这种情况不可能存在. 这里发现一个遗憾:就是求BE的长时要用到非特殊角的三角函数,学生解答时应提供给其具体数据,并且答案要取近似值. 3. 延伸3:如图7,原题中的第二问(直角三角形),当∠AEF为直角时,可得出∠AEC为直角,此时若把∠AEC看作圆周角,此时AC应为直径,由此可设置问题“当点E在以AC为直径的圆上时,求AF的长”.
简解 可将此问题化归为原题中的第二问(直角三角形存在问题),再通过相似求出AF.
4. 延伸4:以上研究△AFG的存在探究问题,尝试研究其周长或面积,拖动点E,发现其面积随着点E的变化而变化,受此启示,尝试渗透“函数”思想,如图8,设AF=x为自变量,△AFG的面积y为因变量,设置问题是“求y与x的函数关系式”.
简解 由于AF∥BC,因此△AFG∽△BCG,设△AFG的高为h, = ,h= ,进而表示出面积.
5. 对于第三问的最值问题可拓展为:隐去中点M,改变问题的形式,将原问中的系数为1的两线段相加变式为系数不等的两线段相加,考查学生思维应变能力,这个问题与原题本质相同,形式不同,关注考查学生对 BE如何合理转化,这就出现了延伸5的问题:求CE+ BE的最小值.
6. 在此基础上,将α的度数进行变化,当α=90°时,如图9,此时菱形就为正方形,问题拓展为:求CE+ BE的最小值,从60度变化为90度,即从菱形变为正方形,如图9,探究对 BE如何转化. 再将问题一般化,α角是一个任意角呢?如图10,求CE+BE·sin 的最小值,设计意图是将BE·sin 转化为EH,CE转化为AE,化折为直,化斜为直,从特殊到一般将问题逐步推向深处.
7. 延伸7:对于最值问题,利用菱形的对角线特征,在此图形中还可做如下的延伸拓展:如图11,取DE中点N,求CM 2+CN 2的最小值.
简解 设BM=x,ME=BM=x,CM 2=OM 2+OC 2=(2 -x)2+22,CN 2=x2+22,CM 2+CN 2=(2 -x)2+22+x2+22=2x2-4 x+20=2(x- )2+14,当x= 时,CM 2+CN 2的最小值为14.
8. 延伸8:受到上述启发,两线段平方和的最值可求,那么两线段的和是否存在最值呢?如图12,由于M,N分别是BE,DE的中点,BD是定长,MN也是定长,基于此思考,还可设问:“取DE中点N,求△CMN周长的最小值”.
现将两种解法呈现如下:
解法1 可将CM+CN转化为含x的两根式相加,进而再转化成平面直角坐标系中两点的距离问题.
解法2 如图12,过点C作CP∥MN,且CP=MN,易得到?荀MNPC,从而CM+CN=CN+NP,而A,C两点关于BD对称,即转化为AP的长,将“一定两动”转化为“两定一动”问题,而MN为定长,从而三角形周长最小值问题得以解决.
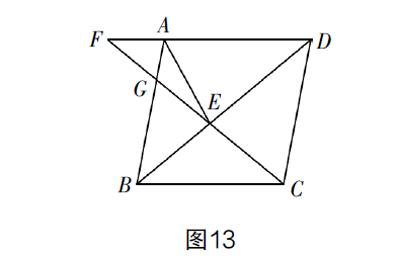
9. 延伸9:进一步挖掘图形特征,如图13,∠ABC为任意锐角,在∠F=∠BAE已证的基础上,而这两角为一线上的两等角,试想如果∠ADB=∠F=∠BAE,这个图形就具备“一线三等角”的图形特征. 顺着这个思路往下走,若∠ADB=∠ABD=∠BAE,相当于EA=EB=EC,因此就加了一个条件:动点E为△ABC的外心,在此前提下,可发现△ADE∽△GFA. 又△GFA∽△GCB,所以△ADE∽△GCB. 这两个三角形中,AD与BC均为已知边,且不是对应边,因此就有了结论:DE·CG为定值.
简解 因为E为外心,可知EA=EB=EC,这就有∠EAB=∠ABE=∠ADE=∠AFG,从而△ADE∽△GFA∽△GCB,所以 = ,DE·CG=AD·CB=4×4=16.
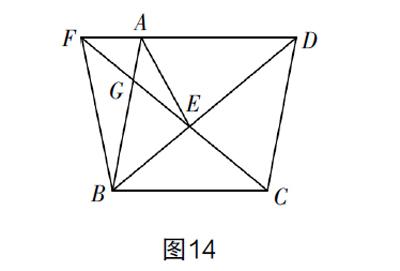
10. 延伸10:如图14,当动点E为△ABC的外心时,发现∠AFE=∠ABE,看到了A,F,B,E四点在同一个圆上,只是“共圆”的证明过程较烦琐,回避这个问题. 从另一角度可以看到△AFG∽△EBG,再进一步得出△AEG∽△FBG,进而得到∠GAE=∠GFB=∠AFG,基于以上这些分析,可设置问题:“求证:EF平分∠AFB”.
简解 E是外心时,可知EA=EB=EC,可得∠EAB=∠ABE=∠AFE,进一步得到△AFG∽△EBG,就有 = ,依此可发现△AEG∽△FBG,从而就有∠GAE=∠GFB=∠AFG,所以EF平分∠AFB.
命题反思
(一)重视教材,关注学生发展
试题应对一线教学具有一定的导向作用与指导价值,引领老师们重视教材,创造性运用教材,引领老师们反思教学,树立以发展学生核心素养为导向的教学意识,在课堂教学中关注知识的内涵,知识间的内在联系,关注几何图形变化过程中的不变性,关注分类讨论转化思想的渗透.
(二)关注能力,提升素养发展
试题源自教材例题、习题,依托图形特征,利于学生找到解决问题的切入口,学生会有似曾相识的感觉,因此可以有效激发学生的主动探究欲望,促进学生的数学思考,在思考的同时关注其能力的发展;同时试题的设计、拓展问题的设置实现了数学内容、思想、方法的高度融合、运用与考查. 试题的解决,需要学生具有逻辑推理、直观想象、数学建模、数学抽象、数学运算等数学核心素养.
(三)恒久坚守,不断追求卓越
数学命题过程辛苦而又孤独,常常是独自一人闭门而思,往往是长时间的不懈思考,为寻求好的问题经常绞尽脑汁,对身心是极大的挑战. 这就需要恒心毅力,以高标准严格要求自我,突破自我,超越自我,把命题过程当作是一次惬意的旅行,不在乎目的地,在乎沿途的风景. 多年的堅守只为了不断追求卓越,命题路漫漫,无畏路途的崎岖,只因初心不改!

