基于非参数回归-粒子滤波模型的公交到站时间预测

张孝梅，陈旭梅，张 溪

(1. 北京交通大学 综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044；2.北京交通发展研究院，北京 100073)

0 引言

随着生活节奏的加快，大众越来越重视时间管理，以期合理分配和高效利用时间。特别是对通勤者而言，时间管理的精细化程度已从以前的1 h逐渐缩短到15 min，甚至更短；与此同时，他们对出行时间的敏感程度也越来越高；若其选择公交方式通勤，则期望尽可能掌握公交到站时间，减少等待时间，提高出行效率。

考虑到公交系统具有较强的时变性、非线性等特点，学者们已提出很多关于公交到站时间预测的算法[1-5]，主要有基于历史数据的模型、神经网络模型[2-3]、支持向量机模型[4]及卡尔曼滤波模型[5]等方法。其中，基于历史数据的模型对历史数据依赖性很高；支持向量机模型的参数确定较为困难且不适用于实时预测[6]；神经网络模型结构较难确定且其存在过拟合或欠拟合的问题[7]；卡尔曼滤波模型是将非线性问题通过函数简化为线性问题，预测精度取决于函数的准确性[8]。

粒子滤波，是一种基于蒙特卡洛思想进行采样的算法，在处理复杂非线性问题时具有优越性[9]。不少学者也探索性地将粒子滤波应用到公交到站时间预测中[10-11]。H Chen[8]提出基于大数据驱动的粒子滤波算法来预测车辆的单程运行时间。H Chen[12]又提出基于非显性状态方程的粒子滤波算法来预测短期、中长期内的车辆运行时间。E Hans[13]等人构建了公交车辆在站停留时间及站间运行时间模型，并利用真实数据对模型参数进行校正，采用粒子滤波算法对固定线路全天的公交到站时间进行预测。任远[7]、B Dhivyabharathi[14]、赵衍青[15]等人将路段进行等长度划分，利用粒子滤波算法对公交车辆在高峰、平峰时段的运行时间进行分段逐步预测。而目前研究成果在涉及对站间速度的预测时，多是采用加权平均的方法简化处理，忽略了速度传达出的实时交通信息，比如天气状况、道路状况等。

为提高预测精度并充分利用数据信息，本研究基于历史数据，利用非参数回归方法对站间速度进行预测，进而利用粒子滤波方法对到站时间进行预测。同时，从速度自身的时变特性出发，在预测站间速度时采用扩展欧式距离作为相似度的度量准则，保证了相似曲线的相似性。本研究所提的方法预测精度较高、鲁棒性较强，为公交到站时间的预测提供了一种新思路。

1 粒子滤波算法概述

Xt=f(Xt-1,Wt-1),

(1)

Zt=g(Xt,Vt),

(2)

式中，Wt-1,Vt分别为系统的过程噪声和观测噪声。

为更好理解粒子滤波公式，本研究引入图1说明。其中，由Xt-1指向Xt的单向箭头表示P(Xt/Xt-1)，即状态值Xt-1与状态值Xt之间的转移概率，由式(1)计算得到；由Xt指向Zt的单向箭头表示P(Zt/Xt)，即状态值Xt与测量值Zt之间的测量概率，由式(2)计算得到。在粒子滤波中，转移概率和测量概率可为任意函数。

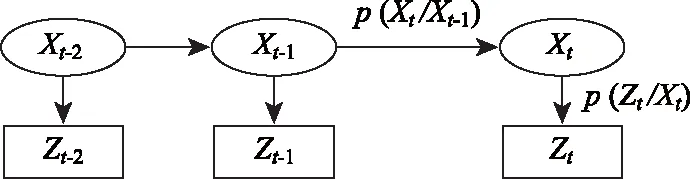
图1 粒子滤波抽象示意图Fig.1 Abstract schematic diagram of particle filtering

本研究采用的粒子滤波算法基于采样-重要性重采样思想。首先借助序贯重要性方法(SIS)进行粒子采样，即可充分利用过去的粒子状态集预测当前的粒子状态集[16]，采样函数服从特定的概率分布q(Xt/X1:t-1)；然后根据当前的粒子状态集及相应权重得到当前系统状态值，权值由式(3)递推估计得到。

(3)

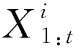
式(3)中，最优的q(Xt/X1:t-1)应为真实的后验概率函数p(Xt/X1:t-1,Z1:t)，但鉴于真实的后验概率函数难以获得，便采用转移概率函数p(Xt/Xt-1)替代q(Xt/X1:t-1)[11]，则式(3)可简化为式(4)，并对权值进行归一化处理[16]，以便得到系统状态值Xt，如式(5)所示。

(4)

(5)

基于序贯重要性采样的粒子滤波会出现粒子退化的现象[12]，即经过一定的迭代次数后，样本的概率分布函数可能会集中于少数粒子，换句话说，是由少量的几个数值代替原来的分布函数。为解决该问题，本研究采用重要性重采样方法进行粒子重采样，做法如下：基于式(5)得到的归一化权值的分布函数作为粒子采样的分布函数,其粒子状态值的确定仍采用转移概率函数p(Xt/Xt-1)[16]。式(3)则进一步简化为式(6)。

(6)

粒子滤波算法流程[10]如下：

Step1：t=0，进行粒子初始化；

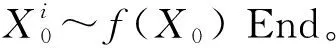
Step2：Fort=1:T。

(1)重要性采样

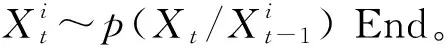
(2)计算权重

Fori=1:N，根据式(6)计算权值 End。

(3)权重归一化

Fori=1:N，根据式(5)使得权值归一化 End。

(4)重采样

根据权值归一化后的分布W(X1:t)，重新采样N次；

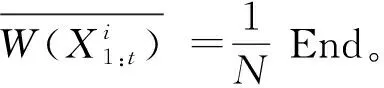
End。

2 公交车辆到站时间预测模型

首先构建了基于粒子滤波算法的公交车辆到站时间预测模型。为提高到站时间模型的预测精度，进一步对模型参数中涉及的站间速度进行预测说明。最后，对预测公交车辆到站时间的算法进行详细阐述。

2.1 到站时间预测模型

公交到站时间构成要素一般划分为站点停留时间、区间运行时间[17-18]、交叉口延误时间[19]等。本研究在描述公交车到站时间的状态方程时，以到站时间为参考点，将站点停留时间及交叉口延误时间等其他构成要素均包含在区间运行时间内，则基于粒子滤波算法的公交到站时间预测模型如下。

状态方程：

(7)

式中，Xt为t站点公交车辆到站时间；A为系数矩阵；Xt-1为t-1站点公交车辆到站时间；Lt为站间距长度；Vt为根据历史数据预测的站间速度；W为系统的过程噪声。

测量方程：

Zt=HXt+V，

(8)

式中，H为系数矩阵；Zt为观测到的公交车辆到达时间；V为测量噪声。

本研究选取A，H为单位矩阵，假设W，V服从高斯分布[7,9]，且二者相互独立。

2.2 站间速度预测模型

在对公交车辆到站时间预测算法介绍之前，先对式(7)中站间速度Vt的预测过程做出详细说明。

假设站间速度是以天为循环周期变化[20]，且不同日期的同一时刻站间速度具有很强的相似性。对站间速度的预测采用非参数预测方法。预测模型的基本思想是，寻找与当前速度趋势相近的速度曲线图，并通过相似度进行衡量，进而得到下一站间速度预测值。因平均站间速度曲线可能具有提前或者滞后的相似性[21]，所以本研究采用扩展欧式距离方法作为评价曲线相似度的度量准则，即分别向前、向后扩展一个数据点，如图2所示。因此，同一条相似曲线的3个相邻点会取3次参与预测站间速度，从一定程度上减少一些噪音干扰，进而保证了相似曲线的精确性。

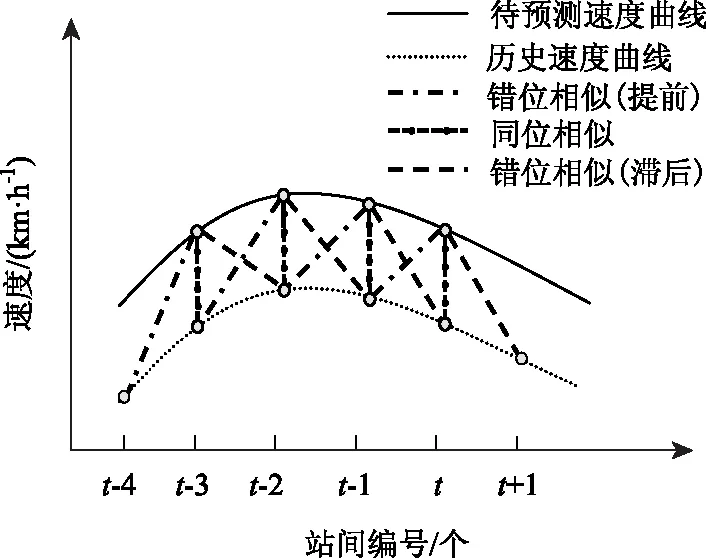
图2 速度曲线相似图Fig.2 Similarity diagram of speed curves

其中，扩展欧式距离公式说明见式(9)～式(11)。式(9)为同位相似曲线对应的计算公式，式(10)为错位相似(提前)曲线对应的计算公式，式(11)为错位相似(滞后)曲线对应的计算公式。

(9)

(10)

(11)

式中，t为待预测站间;j为待预测站间t的前j个站间;Vt-j为待预测速度曲线中站间t-j已预测的速度;V′t-j为站间t-j的历史速度;d为待预测速度曲线与历史速度曲线之间的距离。

预测站间速度Vt的算法流程如下：

Step1：初始化：对线路运行方向前4个站间的站间速度V1，V2，V3，V4进行赋值；

Step2：对该线路其他的站间速度Vt进行顺序预测。

Fort=5∶T。

(1)构建历史数据集：从历史站间速度数据库中挑选出同条线路每天相近时刻运行的站间速度曲线。

(2)根据式(9)～式(11)，挑选出与前4个站间速度Vt-1，Vt-2，Vt-3，Vt-4变化趋势最相似的K条历史曲线。

(3)获取K条历史曲线中站间速度V′t，并根据曲线相似性大小给予权重，预测得到站间速度Vt，见式(12)。

End

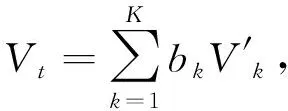
(12)

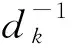
2.3 公交到站时间预测算法流程

基于粒子滤波的公交到站时间预测模型的算法流程如下。

Step 0：选定此次预测的线路编号、日期、时间点。

Step 1：t=0，粒子初始化；

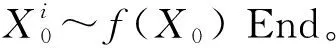
Step2：Fort=1∶T。

(1)重要性采样

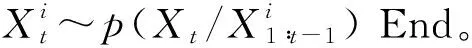
(2)预测

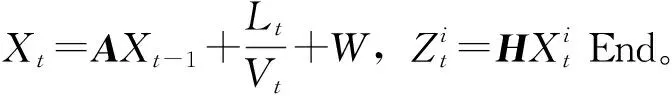
(3)计算权重

Fori=1∶N根据式(6)计算权值 End。

(4)权重归一化

(5)重采样

根据步骤(4)得到的分布W(X1∶t)，产生新的N个粒子，即Xi′t～W(X1∶t)；

End。

3 案例分析

3.1 基础数据描述

为验证模型的有效性及正确性，选取北京市市区3条典型线路(全天客运量均处于较高水平)为研究对象，预测其早高峰时段的公交车辆到站时间。其中，3条线路分别为公交1路(老山公交场站-四惠枢纽站)、特11路(时代庄园北站-宋家庄枢纽站)、300路快车内环(草桥-草桥)。本研究选取2019年3月1日至3月29日共21个工作日的历史GPS速度数据，对4月1日至4月4日在特定时刻(7:30)发车后的区间运行速度进行预测，进而对公交的到站时间进行预测。

本案例选取的公交到站时间观测数据来源于公交车载GPS技术采集的逐秒速度数据；区间长度数据是基于北京市公交线网，借助ArcGIS计算的站间距离；站间平均速度的历史数据是基于逐秒速度数据集成的平均站间速度。考虑3条线路的最大发车间隔(由首发站发车间隔计算得到，受GPS班次数据识别算法的影响)，本研究在选取预测时间点时增加了10 min的弹性时间。如预测某一线路发车时刻为7:30的公交车辆站间运行速度，则从历史速度数据库中选取发车时刻为7:20—7:40的运行数据。需要说明的是，弹性时间越大，预测准确度越高，但也将相对耗时。

3.2 公交到站时间预测结果3.2.1 站间速度预测结果

目前，普遍采用加权平均模型等对站间速度进行预测。图3为利用非参数回归方法、加权平均法两种方法，预测4月1日(星期一)300路快车内环公交发车时刻为7:30的各站间速度的误差对比图。由图可知，非参数回归方法的预测结果与实际值更为接近，而加权平均法预测结果与实际值有较大偏差。

图3 300路快车内环站间速度预测对比Fig.3 Comparison of predicted average speeds between inner ring stops of No.300 express bus

为进一步衡量预测精度，本研究采用平均绝对误差(MAE)、标准误差(RMSE)、平均绝对百分误差(MAPE)3个指标来对两种方法进行评价。计算公式如式(13)～式(15)所示。

(13)

(14)

(15)

式中，Si为区间速度实际值;S′i为区间速度预测值;n为样本量。

早高峰时段(发车时刻为7:30)，3条线路的站间速度预测效果如表1所示。从3条线路的MAE，RMSE及MAPE3个指标可看出，非参数回归法均优于加权平均法；特别是300路快车内环，基于非参数回归方法预测的站间速度平均绝对误差为0.64 km/h，平均绝对百分误差小于1.00%，预测精度较高，为后续预测公交车辆到站时间提供了基础性数据支撑。

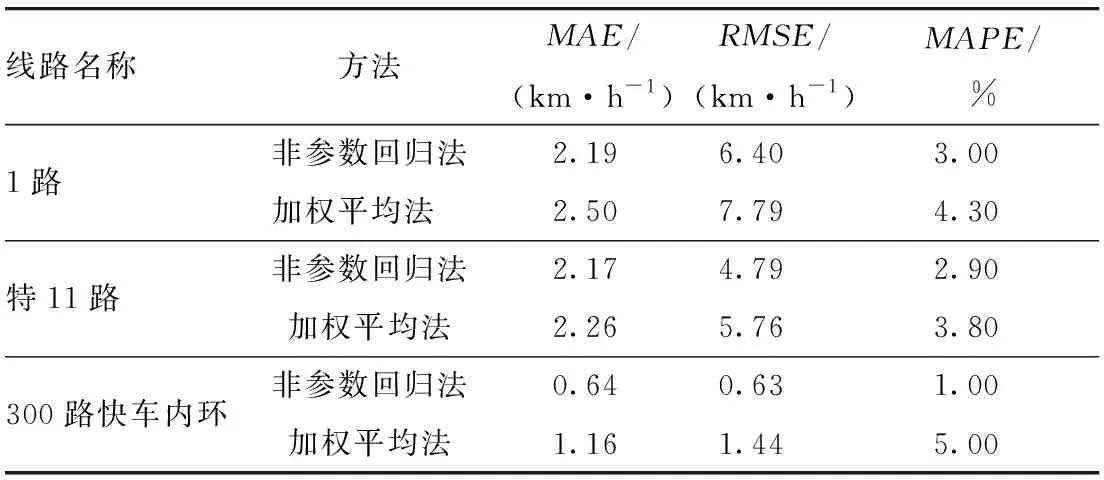
表1 早高峰时段站间速度预测误差汇总表(一周平均)Tab.1 Prediction errors of speed between stops at morning peak hours (one-week average)

3.2.2 到站时间预测结果

图4为利用非参数回归-粒子滤波(本研究所提算法)、加权平均法-粒子滤波、非参数回归-卡尔曼滤波、加权平均法-卡尔曼滤波4种算法，得出的早高峰时段内线路各站点到站时间预测误差(一周平均)的对比图。由图4可知，利用非参数回归-粒子滤波算法得到3条线路的预测结果均优于其他3种方法,且因为3条线路运行情况复杂程度不同，造成预测误差存在差异，300路快车内环的预测效果要明显优于其他两条线路。

表2为利用4种算法得出的线路预测平均误差汇总表，由表可知，从线路角度来看，4种方法中预测效果最好的为非参数回归-粒子滤波，其次是加权平均法-粒子滤波算法和非参数回归-卡尔曼滤波算法，最后为加权平均法-卡尔曼滤波算法；利用本研究所提算法得到的1路到站时间的平均绝对误差均处于1.28 min之内，特11路的平均绝对误差均处于0.97 min之内，300路快车内环的平均绝对误差均处于0.63 min之内；3条线路的标准误差均在3 min内，平均绝对百分误差均小于4%。

图4 到站时间预测误差Fig.4 Prediction errors of bus arrival time

以粒子数目的变化对该模型的敏感度进行分析。以300路快车内环为例，如图5所示，线路平均到站时间预测的估计误差呈带状分布，且随着粒子数目的增多，标准差越小越稳定，即预测效果越好。

4 结论

考虑到速度数据包含众多信息，本研究提出了一种基于非参数回归-粒子滤波算法，利用历史速度数据趋势来预测公交车辆的到站时间模型。

(1)采用非参数回归方法，利用历史趋势来预测站间速度的变化趋势：创造性地对历史数据的选取时刻和站间速度趋势参照点进行拓展，增加模型的预测鲁棒性。结果表明该方法的预测精度高于加权平均方法。

(2)采用粒子滤波算法对公交到站时间进行预测，为避免粒子退化，每次迭代均采用重抽样技术；选取北京市内3条线路，利用非参数回归-粒子滤波(本研究所提算法)、加权平均法-粒子滤波、非参数回归-卡尔曼滤波、加权平均法-卡尔曼滤波4种算法对公交到站时间进行预测，证明了本研究所提算法的优越性；对模型进行敏感度分析，发现随着粒子数目的增多，标准差逐渐稳定在1.1 min左右，说明模型的稳定性较好。

图5 粒子数目对模型敏感度的影响Fig.5 Influence of particle number on model sensitivity

未来拟对公交车辆到站时间预测模型进行深入研究，将公交车辆站间运行时间进行细化，进一步区分出在站停留时间、交叉口候车时间等成分，使得对站间速度、到站时间的预测更加合理。