含砂天然气节流阀冲蚀仿真模拟及结构改进
钱东良, 田辉芳
(山西省燃气规划设计研究院有限责任公司,山西太原030024)
1 概述
由于天然气中含有泥砂,管道输送介质为气-固两相流,在运行过程中,节流阀内部长时间受到气-固两相流(特别是其中的砂粒)的冲击,易发生冲蚀和刺漏等现象,严重影响生产安全。在节流孔处,由于流通面积减小,其压力、速度以及粒子的流动轨迹都发生改变,故此处常常是发生冲蚀较严重的部位[1]。以楔形节流阀阀芯为例,楔形节流阀阀芯失效现场实物见图1[2],阀芯迎流面受到的冲蚀破坏较为严重,直接导致其节流功能失效。

图1 楔形节流阀阀芯失效现场实物
目前,关于节流阀的研究已取得一定的进展,文献[2-4]中对节流阀进行了流场分析,得出其内部流场的分布规律,但是,针对不同类型的节流阀内部易产生冲蚀的具体位置及防护措施并未全部给出。因此,有必要在已有研究的基础上做更进一步的仿真模拟。
本文采用Pro/E 5.0软件建立锥形节流阀和楔形节流阀的几何模型,利用ANSYS Fluent 14.5软件建立仿真模型,模拟得到节流阀内产生冲蚀的具体位置,并在此基础上,针对阀芯进行一定程度的结构优化,通过仿真模拟验证其有效性,从而实现减缓冲蚀的目的。
2 几何模型的描述
节流阀主要由阀体、阀芯、弹簧和调节手轮等部件组成,通常情况下竖直安装,通过阀芯的竖直移动来改变节流孔的流通面积,从而达到节流效果。以规格为DN 50 mm锥形节流阀为例,其简化三维模型见图2,结构尺寸见图3,图3中标注的尺寸均为内壁尺寸,相应的单位为mm,图3中设定的开度是某一工况下的开度,本文以此开度为例进行模拟。
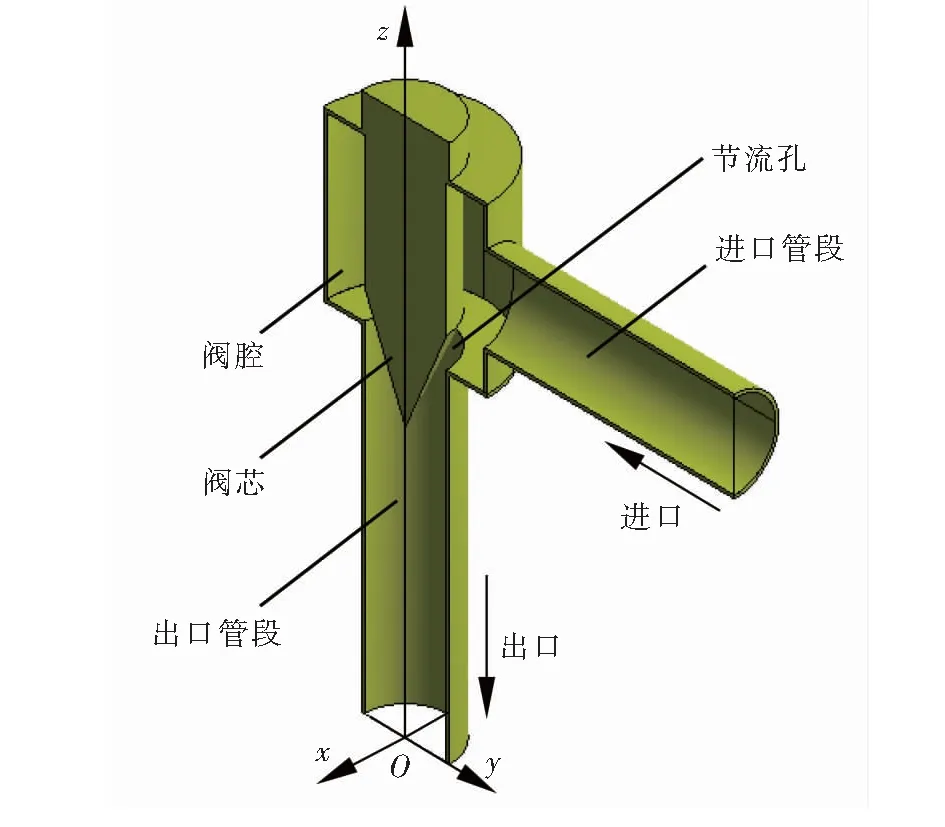
图2 DN 50 mm锥形节流阀的简化三维模型
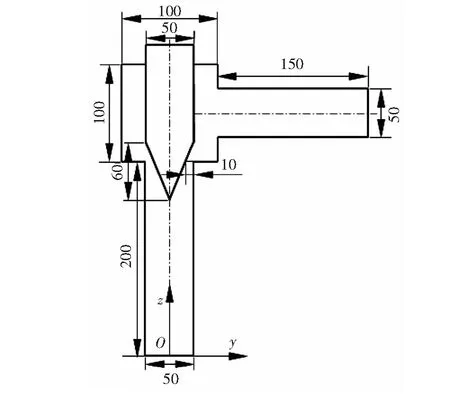
图3 DN 50 mm锥形节流阀的结构尺寸
图2中,三维坐标系的建立以出口端面的圆心为原点O,x轴和y轴均在出口端面所在的水平面上,与进口管段中轴线相垂直的是x轴,与进口管段中轴线相平行的是y轴,阀芯中轴线为z轴。为了方便了解简化模型的内部结构以及节省模拟计算的时间,以yOz平面为中心面进行对称剖分,取其一半进行分析。在三维模型中,弹簧和调节手轮等部件简化为图2中与阀芯相连且凸出阀腔的圆柱部分。节流阀垂直安装,即重力加速度g的方向为-z方向,流体流入方向为-y方向,流体流出方向为-z方向。进口端面、进口管段内壁、阀腔内壁、阀芯外壁、出口管段内壁、出口端面及yOz平面共同组成的空间区域即为计算域,利用ANSYS Fluent 14.5进行建模分析时,只需研究该计算域即可。
本文以应用比较广泛的锥形节流阀和楔形节流阀为基础研究对象,并在其现有结构的基础上,针对阀芯进行一定的结构改进,其中,将锥形节流阀阀芯的顶端(尖端)改为圆台状,将楔形节流阀阀芯改为圆台状阀芯或三段式阀芯,得到3种优化的结构形式,分别为圆台状阀芯锥形节流阀、圆台状阀芯楔形节流阀和三段式阀芯楔形节流阀。利用Pro/E 5.0建立不同类型节流阀的三维几何模型,锥形节流阀和圆台状阀芯锥形节流阀的几何模型见图4,楔形节流阀、圆台状阀芯楔形节流阀、三段式阀芯楔形节流阀的几何模型见图5。

图4 锥形节流阀和圆台状阀芯锥形节流阀的几何模型

图5 楔形节流阀、圆台状阀芯楔形节流阀、三段式阀芯楔形节流阀的几何模型
3 网格划分
将建立的几何模型导入ANSYS Workbench中的Geometry里,应用Fill功能填充计算域,完成后将其导入Mesh中划分网格。以进口处的网格划分为例,进口处网格划分见图6。
整个模拟区域可分为湍流核心区和边界层区。在网格划分的过程中,湍流核心区采用自动划分网格,以四面体网格为主。边界层区添加边界层网格,对近壁面处的网格进行局部加密,在计算过程中,使用壁面函数法来处理该区域,壁面函数法的具体分析详见4.5.1条,其目的在于将壁面上的物理量和湍流核心区相应的物理量联系起来。边界层网格的划分方式采用First Layer Thickness,边界层网格划分需要设置的参数为:第1层网格高度(First Layer Height)为1.0 mm,边界层数(Maximum Layers)为5层,网格渐变率(Growth Rate)为1.05,这样能够保证无量纲距离y+处于(30,60)范围。
4 数学模型
4.1 数学模型概述
本文研究的对象是气-固两相流,其中,天然气作为连续相,砂粒作为离散相。为了简化模拟计算,本文假定天然气介质为不可压缩流体且流动是稳态的,天然气的密度不随空间位置和时间变化,流场处于完全发展的湍流状态,忽略流体分子之间黏性的影响,在该假定情况下能够满足工程仿真模拟精度的要求。
采用ANSYS Fluent 14.5软件进行冲蚀仿真模拟需要建立合适的数学模型,它主要包括:内部流场计算、颗粒轨迹计算和冲蚀速率计算。连续相采用RNGk-ε湍流模型,离散相采用离散相模型,通过交替求解连续相控制方程和离散相运动方程来实现连续相与离散相的双向耦合;冲蚀速率模型采用ANSYS Fluent 14.5中定义的冲蚀速率公式;近壁面区域采用标准的壁面函数法进行处理;采用有限体积法对控制方程进行离散化处理;采用SIMPLE算法求解速度场与压力场的耦合。
4.2 湍流模型
节流阀连续相计算必须选用合理的湍流控制方程。根据流体动力学理论,RNGk-ε湍流模型对具有分离和二次流的湍流流动具有较好的模拟性[5],既适应于高雷诺数的湍流流动,也适应于低雷诺数的湍流流动,其模型常数是利用重整化群(RNG)方法精确推导出来的[6]。RNGk-ε湍流模型是半经验公式。
k方程见式(1)[5]:
Eg+Eb-ρε-EM+Sk
(1)
式中ρ——天然气(不含砂粒)密度,kg/m3
k——湍流动能,J
t——时间,s
i——取值为1、2、3,分别对应x轴、y轴、z轴
ui——速度分量,分别对应x轴、y轴、z轴上的速度分量ux、uy、uz,m/s
xi——对ui求偏导时对应的x轴、y轴、z轴的坐标,m
Prk——k方程的湍流普朗特数
μeff——有效动力黏度,Pa·s
j——取值为1、2、3,分别对应x轴、y轴、z轴
xj——对k求偏导时对应的x轴、y轴、z轴的坐标,m
Eg——层流速度梯度产生的湍流动能,J
Eb——浮力产生的湍流动能,J
ε——湍流耗散率,J/s
EM——湍流流动中波动对整个能量耗散的贡献,J
Sk——k方程中与实际问题有关的修正项,由用户自定义,无因次
需要注意的是:ui、xi、xj均为笛卡尔张量记法,均表示1组分量,1个含有3个与坐标相关的独立变量集合用1个下标表示,例如,对于坐标x、y、z可表示为xi(i=1,2,3),即x1表示x轴坐标,x2表示y轴坐标,x3表示z轴坐标;对于x轴、y轴、z轴上的速度分量ux、uy、uz可表示为ui(i=1,2,3),即u1表示ux,u2表示uy,u3表示uz。以上表示方法为流动方程表达式中惯用的张量记法。在式(1)中关于xi、xj的偏导数表示下标i和j分别为1、2、3时的各项之和,即式(2)和式(3)。
(2)
(3)
ε方程见式(4)[5]:
(4)
式中Prε——ε方程的湍流普朗特数
C1ε、C2ε、C3ε——经验常数,无因次
Rε——ε的函数
Sε——ε方程中与实际问题有关的修正项,由用户自定义,无因次
4.3 离散相模型
离散相模型将天然气作为连续相、砂粒作为离散相进行处理,离散相与连续相间通过实时进行质量、动量和能量交换实现双向耦合求解。离散相模型在应用中忽略砂粒之间的相互作用以及砂粒的体积对连续相的影响,应用离散相模型的前提是离散相的体积分数应小于10%。文献[7]针对砂粒运动方程、砂粒受力分析、离散相边界条件的设置以及离散相与连续相的耦合等方面进行了详尽的分析。
4.4 冲蚀速率模型
节流阀内壁面的冲蚀失效程度可以通过计算全部砂粒在天然气携带下冲击节流阀内壁而产生的冲蚀速率来表示,冲蚀速率模型采用ANSYS Fluent 14.5中定义的冲蚀速率公式,该冲蚀速率模型在文献[5]中已经做了详尽的分析。
4.5 其他相关数值计算方法
4.5.1 壁面函数法
针对近壁面区域有2种处理方式:① 采用低雷诺数k-ε模型来直接求解黏性影响比较明显的黏性底层和过渡层区域;② 不直接求解该区域,而是应用壁面函数法,即用一组半经验公式将壁面上的物理量与湍流核心区内的相应物理量联系起来。采用低雷诺数k-ε模型时,因黏性底层和过渡层内的物理量变化大,需要划分较为细密的网格才能满足计算要求,计算成本较高。与前者相比,壁面函数法能够处理各种不同壁面流动问题,且具有计算效率高和工程实用性强的优点。因此,在本文的研究中,对近壁面区域采用标准的壁面函数法[7]27-29。
4.5.2 控制方程的离散方法
对控制方程采取不同的离散方式将会产生不同的数值求解方法,根据离散原理的不同主要分为有限差分法、有限元法和有限体积法。有限差分法对复杂几何体适应性较差,近年来已经逐渐被有限元法和有限体积法代替。有限元法相对有限差分法,能够处理复杂的几何边界条件,在固体力学的仿真计算中使用较多,但在流体力学计算中应用极少。有限体积法不仅具有有限差分法良好的守恒性,而且能够和有限元法一样,处理复杂的边界条件,在流体力学的仿真计算中有着良好的适用性[7]29。ANSYS Fluent 14.5就是使用有限体积法来离散Navier-Stokes方程的。
4.5.3 SIMPLE算法
ANSYS Fluent 14.5中包括3种压力-速度耦合算法:SIMPLE算法、SIMPLEC算法和PISO算法。前2种主要应用于稳态问题计算,PISO算法在用于计算瞬态问题时具有一定的优势。在工程实际中,SIMPLE算法一般用于不可压缩流体的仿真计算,经实践检验是一种求解流体力学中流动问题的十分成功的算法之一。SIMPLEC算法在本质上与SIMPLE算法相同,理论上相当于采用不同的松弛因子的效果,故只要在SIMPLE算法中采用合适的松弛因子,即可达到与其他算法相同的收敛速度。因此,本文在数值模拟过程中选用SIMPLE算法来求解速度场与压力场的耦合[7]30-31。
5 各项设置
① 模型设置
应用ANSYS Fluent 14.5中的离散相模型,开启Erosion/Accretion物理模型。计算过程中,对控制方程组的离散采用有限体积法,扩散项采用二阶迎风差分格式,压力-速度耦合采用SIMPLE算法,湍流模型采用RNGk-ε双方程,利用拉格朗日法对通过流场的颗粒进行逐个追踪。
② 边界条件设置
进口设置为速度进口(velocity-inlet),出口设置为自由出流(outflow),即在出口处的流动为充分发展的,各个变量(压力除外)沿流动方向的梯度为0,离散相均设置为逃逸(escape),壁面设置为无滑移壁面。
③ 其他设置
节流阀的规格为DN 50 mm。
进口处流体的速度为5 m/s,压力为1.1 MPa,常温输送。整个模型重力场加速度为9.8 m/s2。
节流阀的材料采用碳素钢,碳素钢密度为7 850 kg/m3,碳素钢法向反弹系数en的各项取值[7]24为0.993、-0.031、4.75×10-4、-2.61×10-6,碳素钢切向反弹系数et的各项取值[7]24为0.998、-0.029、6.43×10-4、-3.56×10-6。
砂粒质量流量为0.000 5 kg/s,砂粒密度为1 500 kg/m3,砂粒直径为150 μm,砂粒形状系数为0.53,砂粒直径函数的取值[7]27为1.8×10-9,速度分量函数的取值[7]27为2.6,冲击角度函数的取值[7]27见表1。
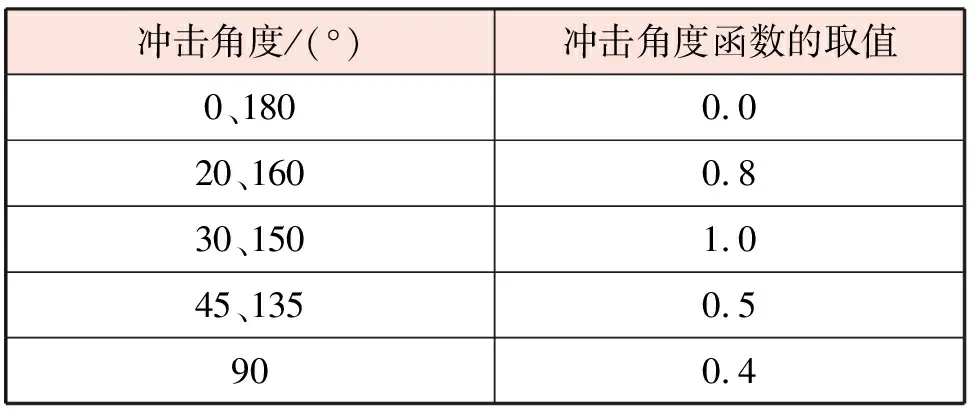
表1 冲击角度函数的取值
本文假定天然气介质为不可压缩流体且流动是稳态的,天然气的主要组分是甲烷,因此,模拟时连续相选择甲烷,与甲烷有关的ρ、μeff等参数取系统默认值;Prk、Sk、Prε、C1ε、C2ε、C3ε、Rε、Sε等其他相关参数取系统默认值。
6 求解
求解控制参数:ANSYS Fluent 14.5基于有限体积法对控制方程进行离散和求解,在Solution Methods中,压力速度耦合选择SIMPLE。Gradient选择Least Squares Cell Based,Pressure选择Second Order,Momentum、Energy、Diffusive Phase均选择Second Order Upwind。
亚松弛因子:在Solution Controls 中,Pressure、density、Body Force分别取0.3、1、1,Momentum、Energy分别取0.7、1。
残差设定:Energy为10-5,其他均为0.001。
初始化:初始化方法选择Standard Initialization,选择Initialize从进口端面开始计算,经过迭代计算,得到结果。
7 模拟结果分析
7.1 锥形节流阀模拟结果分析
锥形节流阀冲蚀速率云图见图7,图7中的色标右面的标值为冲蚀速率的数值,相应的单位为mg/(cm2·a)。

图7 锥形节流阀冲蚀速率云图(软件截图)
由图7分析可知,锥形节流阀内部产生冲蚀的具体位置分为3个部分:①阀芯迎流壁面处,呈半椭圆状区域,冲蚀速率相对较大;②阀芯与节流孔交接处,呈圆环状区域,其中,在背对阀芯迎流壁面的一侧靠近yOz平面的节流孔位置附近冲蚀速率最大;③出口管段内壁面处,呈长条状区域,冲蚀速率相对较小,冲蚀区域面积较大。
综合分析以上3个冲蚀位置,本文将出口管段作为冲蚀控制的主要区域,其主要原因包括以下3个方面:①出口管段的冲蚀面积较大,更需要加以控制;②通过采取改进阀芯结构的方式,容易实现对出口管段的冲蚀控制;③虽然阀芯迎流壁面处和阀芯与节流孔交接处的冲蚀速率均比出口管段内壁面处大,但是这两处的冲蚀不可避免,故本文不做研究。
锥形节流阀粒子迹线图见图8,图8中的色标右面的标值为砂粒编号的数值,以图8中编号为第5 900号的砂粒的迹线为例,其颜色为红色,由进口至出口构成其完整的运动轨迹。
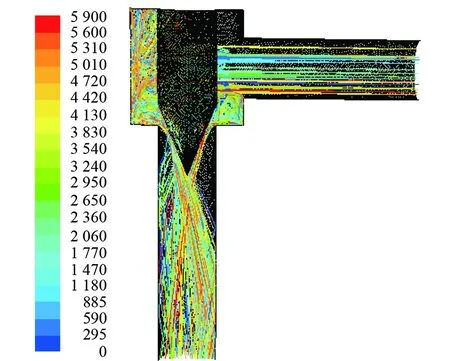
图8 锥形节流阀粒子迹线图(软件截图)
将图8中砂粒迹线与壁面相交的位置与图7中的冲蚀位置相对比,两者的位置基本一致,因此,砂粒迹线与壁面相交的拐点即为冲蚀点,由此可以判定冲蚀产生的原因主要是气体携带的砂粒不断冲击和切削壁面所致。
由图8分析可知,砂粒与阀芯迎流壁面碰撞反弹后,在背对阀芯迎流壁面处产生一定的积聚,积聚后的大量砂粒经节流孔处yOz平面两侧位置进入出口管段,在背对阀芯迎流壁面的一面靠近yOz平面的节流孔位置附近,砂粒与阀芯壁面接触的相对速度和频率比其他位置都大,因此,在该位置产生的冲蚀速率最大。
以下图9~16,类似的云图中关于色标标值的含义和单位分别与图7和图8一致。
7.2 圆台状阀芯锥形节流阀模拟结果分析
圆台状阀芯锥形节流阀冲蚀速率云图见图9,粒子迹线图见图10。
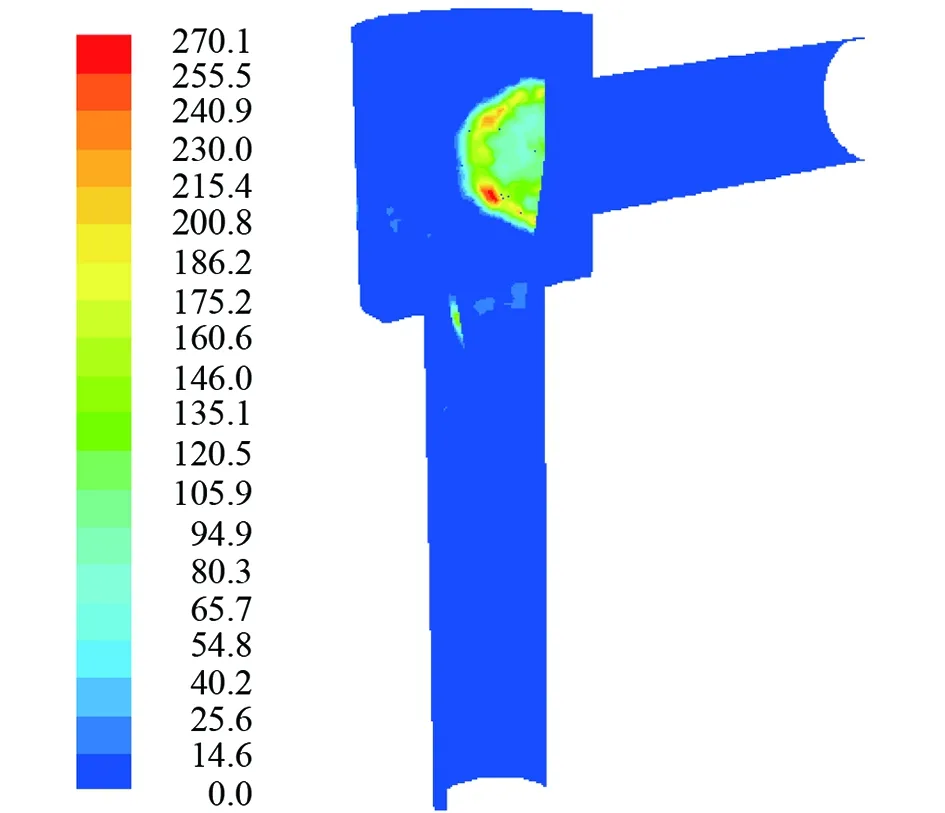
图9 圆台状阀芯锥形节流阀冲蚀速率云图(软件截图)
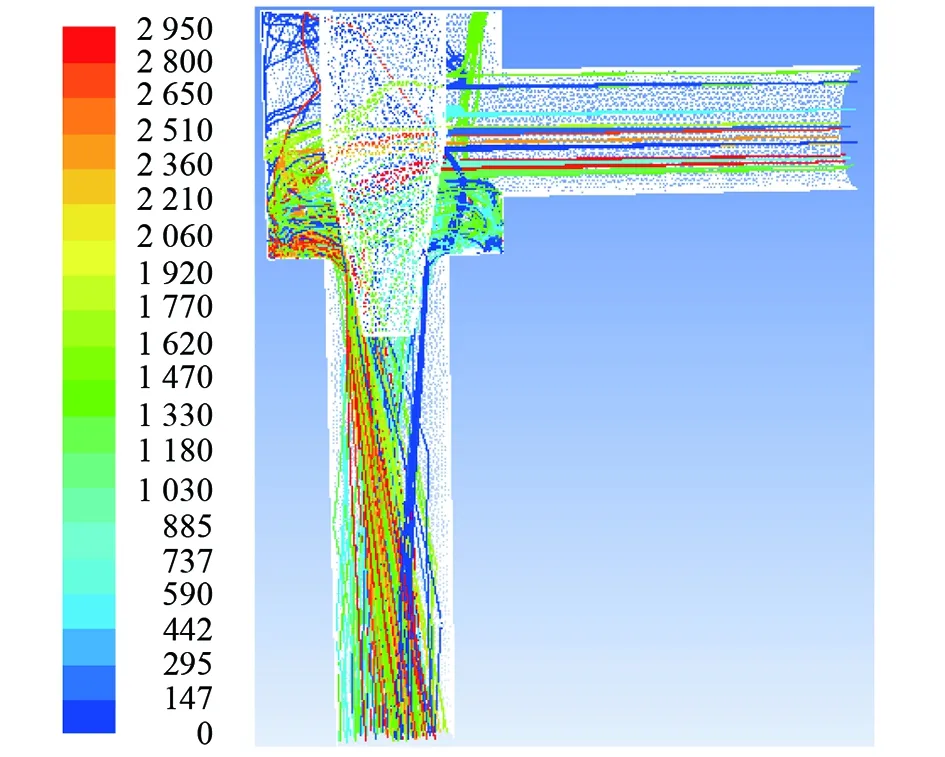
图10 圆台状阀芯锥形节流阀粒子迹线图(软件截图)
由图9分析可知,阀芯迎流壁面处和阀芯与节流孔交接处产生冲蚀,出口管段基本无冲蚀破坏。与图7相比,出口管段的冲蚀得到明显改善。
由图10分析可知,经节流孔后砂粒的轨迹受到阀芯结构改变的作用顺势向下,只有少数的砂粒碰撞到壁面,避免了出口管段内壁面受到较大冲击。
图9、10证明了改进后的阀芯结构既能够满足节流效果,又能够针对出口管段起到一定减缓冲蚀的作用。
7.3 楔形节流阀模拟结果分析
楔形节流阀冲蚀速率云图见图11,粒子迹线图见图12。

图11 楔形节流阀冲蚀速率云图(软件截图)

图12 楔形节流阀粒子迹线图(软件截图)
由图11、12分析可知,楔形节流阀内部产生冲蚀的具体位置为阀芯迎流壁面处和出口管段内壁面处;最大冲蚀速率发生在阀芯迎流壁面处,是由砂粒与阀芯迎流壁面相碰撞产生较大的冲击和切削作用所致;砂粒在与阀芯壁面碰撞反弹后直接进入出口管段,在节流孔处无冲蚀破坏,在出口管段内壁面处产生的冲蚀区域较大。
7.4 圆台状阀芯楔形节流阀模拟结果分析
圆台状阀芯楔形节流阀冲蚀速率云图见图13,粒子迹线图见图14。
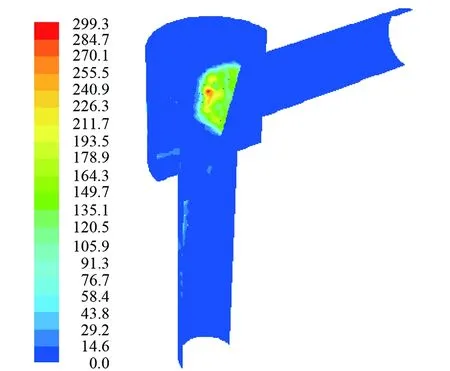
图13 圆台状阀芯楔形节流阀冲蚀速率云图(软件截图)
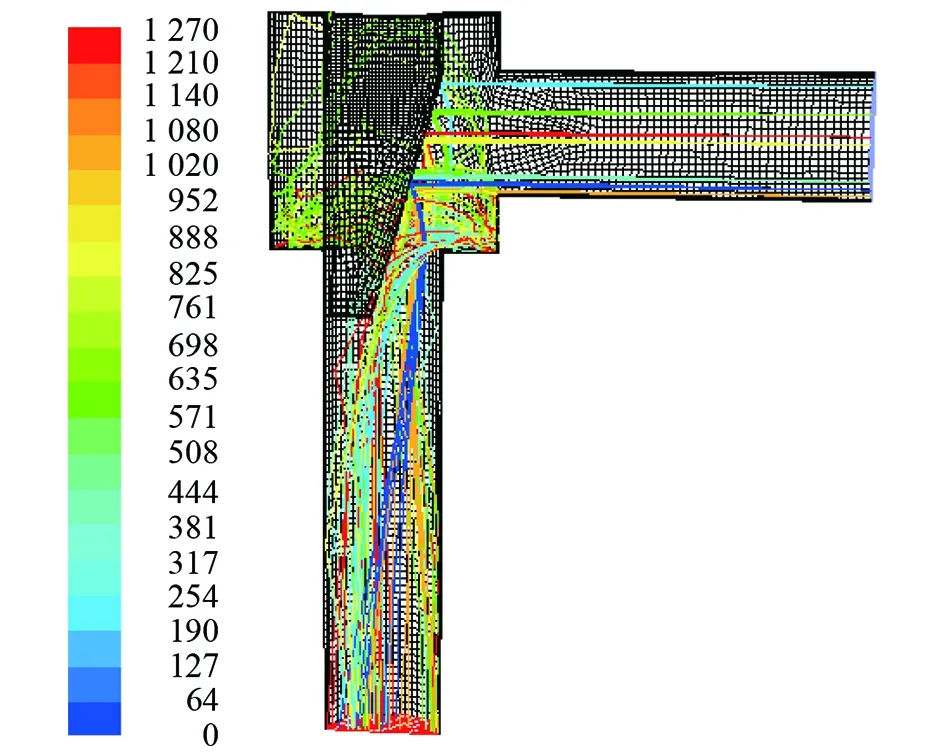
图14 圆台状阀芯楔形节流阀粒子迹线图(软件截图)
由图13分析可知,产生冲蚀的主要区域为阀芯迎流壁面处,该处的冲蚀速率最大,与图11的冲蚀情况基本一致,证明了阀芯迎流壁面处受到的冲蚀是不可避免的。
由图14分析可知,该阀芯结构能够为气流及砂粒提供一定的导向作用,经过节流孔后砂粒的轨迹发生了部分改变,对出口管段内壁面的冲击变小。
与图11相比,出口管段的冲蚀区域和冲蚀速率都明显变小,节流阀出口管段的冲蚀得到了一定的控制。
7.5 三段式阀芯楔形节流阀模拟结果分析
三段式阀芯楔形节流阀冲蚀速率云图见图15,粒子迹线图见图16。

图15 三段式阀芯楔形节流阀冲蚀速率云图(软件截图)

图16 三段式阀芯楔形节流阀粒子迹线图(软件截图)
为了方便模拟结果的分析,现将三段式阀芯楔形节流阀的阀芯结构分为上、中、下三段,其中,阀芯上部圆柱段为阀芯上段,阀芯中部与阀芯中轴线斜交段为阀芯中段,阀芯下部与阀芯中轴线平行段为阀芯下段。由图15、16分析可知,冲蚀速率最大的位置为阀芯下段,主要是由于阀芯下段改变了砂粒的轨迹,此处壁面受到的冲击和切削作用最大,故冲蚀速率也最大;与此同时,阀芯下段对节流效果影响较小,故实现了冲蚀破坏向对节流效果影响较小区域位置的转移;由于三段式阀芯结构避免了大量砂粒直接冲击出口管段内壁面,使得出口管段内壁面的冲蚀速率减小,起到了减缓冲蚀的作用。
另外,三段式阀芯楔形节流阀还能够弥补楔形节流阀不易改变砂粒流向以及圆台状阀芯楔形节流阀节流效果差的缺陷。
8 冲蚀的预防和减缓措施
为了预防和减缓冲蚀破坏的发生,在设备构件本身因素方面,除本文中提出的改进阀芯结构的方法外,还可以在阀芯迎流壁面处采用耐冲蚀的材料、涂层保护以及加装硬质合金套等措施,以提高阀芯的强度和耐磨度来减缓冲蚀。
对于节流阀出口管段内壁面的冲蚀破坏,可以通过结构上的改进来控制。目前最常用的方法是安装防冲刺短节[8],用防冲刺短节替代出口管段,在防冲刺短节入口段加装硬质合金套,加大防冲刺短节的中段腔室,在防冲刺短节出口处加装硬质合金套球头[9]。
在流动介质因素方面,可以采取适当措施减少砂粒的含量。
在人为因素方面,关停和再启动时应注意保持平稳性,不断更新升级检测设备,加大检测频率,及时发现问题,及时更换,加强预防。
9 结论
① 在气-固两相流条件下,节流阀内部的冲蚀破坏不可避免。
② 节流阀内部产生冲蚀破坏的位置为阀芯的迎流壁面处、阀芯与节流孔交接处以及出口管段内壁面处,软件模拟结果与现场冲蚀失效情况一致。
③ 3种改进后的阀芯结构在一定程度上均改变了砂粒的运动轨迹,减小了对出口管段内壁面的冲蚀,对节流阀冲蚀控制的主要区域起到一定的保护作用。
④ 除采取改进阀芯结构的方法外,还可以通过采用耐冲蚀材料、涂层保护、加装硬质合金套、加装防冲刺短节等措施减缓节流阀内部的冲蚀破坏。

