王正非林火蔓延模型改进研究
张晓婷,刘培顺*,王学芳
(1.中国海洋大学信息科学与工程学院,山东 青岛 266000;2.中国海洋大学数学科学学院,山东 青岛 266000)
由于全球气候日渐变暖,近年来森林火灾发生的频率和规模十分反常,对人类、环境和经济造成了前所未有的危害,森林火灾已经成为生态文明建设和森林资源安全的最大威胁。森林火灾蔓延模型可以对火灾的发生、发展以及变化趋势进行精确地灾情分析和评估,还可以准确的模拟灾情使预估结果可视化,能够帮助专家进行决策,为救灾工作提供帮助。
多年来国内外学者对此进行了深入研究,取得很多成果[1]。目前比较经典的林火蔓延模型有:美国的Rothermel模型[2]、加拿大森林火险等级系统[3]、澳大利亚的McArthur模型[4]和中国的王正非模型[5]。美国的Rothermel提出的林火火峰蔓延模型,是基于能量守恒定律的物理机理模型。此模型的实用性很广泛,但是所需参数太过繁多且不易获取,而且此模型对可燃物的要求很苛刻,要求建立在均一的可燃物状态下,因此只适用于一维方向上的蔓延方向及速度的预测。加拿大国家林火预报系统给出的试验模型主要是侧重坡度对林火蔓延速度的影响,在遇到与实验数据不符的情况时,精度下降。澳大利亚的Noble I.R.等人提出的McArthur模型的林火蔓延速度仅由火险指标和风速等气象因子确定,忽略了可燃物本身的因素。
国内的王正非教授针对我国森林的情况,给出了基于可燃物类型、风速和坡度等的林火蔓延模型[5],在我国适应范围最广。王正非林火蔓延模型(以下简称“王正非模型”)虽然是目前国内比较先进的模型,但是由于林火行为的复杂性,目前此模型还没有达到真正的普遍适用于所有的林火实际蔓延行为,仍存在许多不足。本文将结合已有的成果进一步改进王正非模型,主要是增加了可燃物湿度对林火蔓延速度的影响,改进了各种坡度对林火蔓延行为的影响,使其对林火蔓延情况的预估更为精准。
1 王正非林火蔓延模型
影响林火蔓延速度、蔓延方向和蔓延面积的因素有很多,主要包括两大方面:可燃物性质和环境因素[6]。可燃物性质分为可燃物的类型、湿度、密度等;环境因素包括地形变化(坡度和坡向)、温度、湿度、风速、风向等。其中的可燃物类型、风速、坡度、可燃物湿度对林火蔓延行为的影响比较大。
王正非模型选取可燃物类型、风速、坡度作为主要影响因子对林火蔓延情况进行预测。该模型是建立在大量的实验数据的基础之上,属于统计模型。王正非教授给出的林火蔓延速度方程如下:
其中,R表示预估火灾蔓延速度(m/min);
R0表示初始蔓延速度(m/min);
Ks表示可燃物类型修正系数,随时间和地点而改变的常数;
Kw表示风力修正系数;
cosφ表示坡度修正系数;
φ表示坡度。
下面给出各参数获取方法。
1.1 初始蔓延速度R0的确定
王正非教授给出的初始蔓延速度R0是在室内燃烧(或无风)的条件下给出的,是由火强度的公式反求得到的,如下式:
其中,L为发火点与火峰前缘的最大距离(m),t为时间(min)。此公式是一个实验公式,必须经过实验才能获得一定条件下的林火初始蔓延速度。
1.2 可燃物类型修正系数Ks的确定
可燃物类型是指具有明显的代表植物种、可燃物种类、形状、大小、组成以及其它一些对林火蔓延和控制有影响的特征相似或相同的复合体[7]。不同可燃物类型对林火蔓延速度的影响不同,比如草甸比针叶林更易燃,且草甸着火后的蔓延速度比针叶林快[8]。
由于王正非教授给出的可燃物修正系数Ks在可燃物类型方面没有详细分类[9],无法进行精确计算,郑焕能教授对该问题进行了深入研究,得到可燃物类型影响因子Ks经验常数表[10],见表1。

表1 可燃物类型对林火蔓延速度的修正系数 KsTable 1 Correction coefficient Ks of combustible type to forest fire spread speed Ks
1.3 风速修正系数Kw的确定
风因素分为风速和风向。一般来说,风方向便是林火火头的蔓延方向,而风速则直接影响了林火的蔓延速度。众所周知,风速越大,林火在风方向的蔓延速度越大,风速修正系数Kw越大。当可燃物为草甸,坡度为零(即平地)时,根据王正非对林火蔓延实验的实验记录(见表2),取指数函数为经验回归方程类型,利用一元回归的方法得到风速与火速的经验公式:
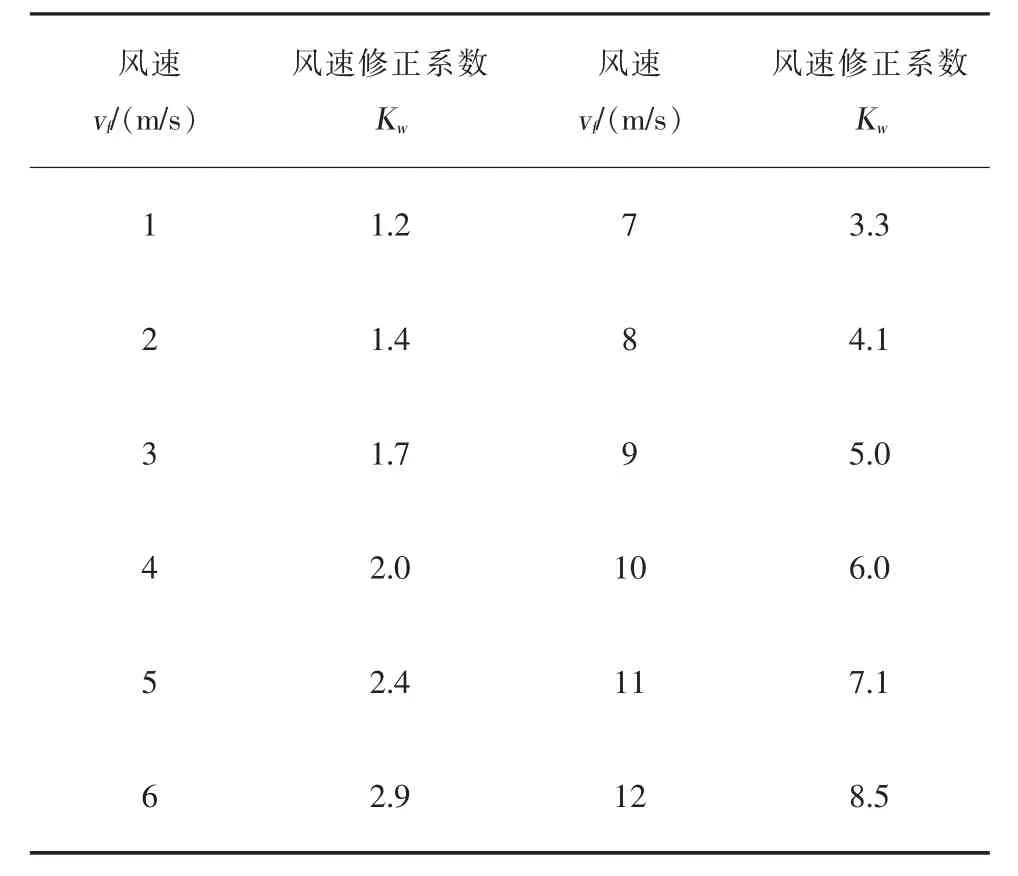
表2 风速对林火蔓延速度的修正系数KwTable 2 Correction coefficient of wind speed to forest fire spread speed Kw
其中,vf表示风速;Kw表示风速修正系数。
1.4 坡度修正系数Kφ的确定
地形中的坡度和坡向则是林火蔓延速度的另一主要影响因素。通常上坡火蔓延速度快,下坡火蔓延速度慢。坡度越大,降水易流失,可燃物越干燥,间接加速林火蔓延。坡向不同也会影响可燃物湿度,向阳坡有太阳光照射,可燃物湿度小,易燃;反之,可燃物湿度大,不易燃。
国外的Lawson提出了蔓延因子公式[11]为:
其中,SF为蔓延因子,δ为斜地面每百米上升的高度。
加拿大国家林火预报系统根据上式进一步求出了上坡、下坡两个方向的蔓延速度,给出的坡度影响因子Kφ为:
其中,Φ为地形坡度角。
王正非教授给出的坡度对林火蔓延速度的影响因子,见表3。表中的正坡度指的是林火上山蔓延时的坡度,负坡度指的是林火下山蔓延时的坡度。
毛贤敏等人则考虑风向和地形的组合,对坡度影响因子Kφ继续改进,导出了上坡、下坡、左平坡、右平坡和风方向的五个方向的方程组,使该模型更更适用于实际[12],此模型在目前的林火蔓延情境中应用广泛。风向和地形结合后的模型为:
1.5 模型存在的不足
王正非教授的模型主要存在两个不足:
不足一:此模型在初始蔓延速度R0的确定上,只是在室内(或无风)条件下,根据实验数据给出初始蔓延速度R0,对可燃物与蔓延速度的关系没有进一步研究,无法推广。在初始蔓延速度R0的确定上目前没有任何研究给出模型。
不足二:在坡度影响因子Kφ的模型关系式中,正切函数在计算一些随机地形坡度角时,会出现计算困难和结果不准确的问题,导致最终的计算结果不准确。而且,即使使用王正非教授给出的经验值,也是一个区间内的坡度对应一个坡度影响因子,导致计算结果不准确。

表3 坡度对林火蔓延速度的影响因子 KφTable 3 Impact factors of slope on forest fire spread speed Kφ
2 改进的林火蔓延模型
本文在林火蔓延模型的建立中,除了考虑可燃物类型、坡度、风速三大影响因素以外,重点研究可燃物湿度对林火的初始蔓延速度R0(即无风时在水平方向上的火蔓延速度,仅取决于可燃物类型与可燃物湿度)的影响,结合改进后的坡度影响因子实现风向与坡度的更准确结合,最终实现对林火蔓延速度预估模型的整体改进。
2.1 林火初始蔓延速度R0
影响初始蔓延速度R0的因素主要与可燃物本身性质有关,外界环境因素(如风和坡度等)影响次之[13]。受条件所限,本文仅研究可燃物湿度与初始蔓延速度R0的影响因子,给出初始蔓延速度R0与可燃物湿度之间的关系式。
根据可燃物湿度可以判断可燃物燃烧的难易程度,及火灾发生后火势和林火蔓延速度等[14]。王正非模型中的初始蔓延速度R0仅适用于实验情况下的R0判断,当实际情况与实验数据不符时,导致模型精度下降。
本文利用西南林学院气象教研室收集安宁县、楚雄市的有关气象资料、森林火灾资料以及小气候观测原始数据,选取其中6组点烧实验数据[15]。可燃物湿度是使用相对应的仪器精准测量得到,初始蔓延速度R0是实验数据,即单位时间内的火蔓延速度,整理可燃物湿度与初始蔓延速度R0的对应表,见表4。
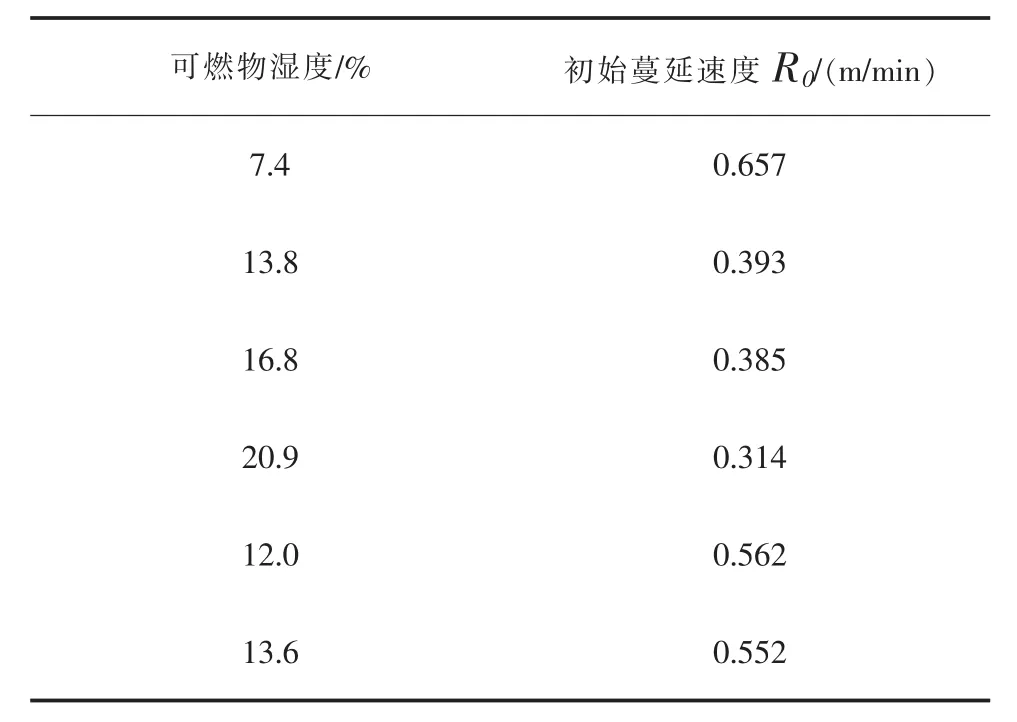
表4 可燃物湿度与初始蔓延速度R0的对应表Table 4 Correspondence table between combus-tible humidity and initial propagation velocity R0
不考虑其他因素对初始蔓延速度的影响,即暂时将其他因素看做常数,取指数函数为经验回归方程类型,利用一元回归的方法得到可燃物湿度与初始蔓延速度R0的关系式:
其中,m为可燃物湿度(%),R0为初始蔓延速度(m/min)。
为了使实验值与计算值的对比更直观、明显,图1展现了两组数据的对比情况,r平方值为0.8415,将其开方得到相关系数r=0.9201。
根据得到的模型关系式,将可燃物湿度依次代入,得到模型计算值,与实验值进行对比,见表5。

表5 初始蔓延速度R0的实验值和计算值的对比表Table 5 Comparison table of experimental and calculated values of initial propagation velocity R0
综上可见,可燃物湿度对初始蔓延速度R0的影响极高,可以在实际火情中,应用可燃物湿度对初始蔓延速度R0进行简易判断,提高了预估林火蔓延速度的效率。
2.2 林火蔓延速度R
王正非模型中影响林火蔓延速度R的因素主要有四个:初始蔓延速度R0、风速、可燃物类型、坡度。本节采用王正非教授出的坡度影响因子经验值,得到坡度与影响因子Kφ的散点图。下坡及平坡坡度修正系数,见图2;上坡坡度修正系数,见图3。横坐标为坡度,纵坐标为坡度影响因子Kφ。
利用一元回归的方法得到坡度与影响因子Kφ的线性回归模型公式为:
其中,w为坡度,Kφ为坡度影响因子。下坡及平坡(w≤0)时,r平方值为 0.9814,将其开方得到相关系数 r=0.9907;上坡(w>0)时,r平方值为 0.9773,将其开方得到相关系数r=0.9886。
最终,得到的林火蔓延速度改进模型为:
3 模型测试与结果对比
为了验证此次改进模型的精确程度,本文以于良成等人在铁岭、开原以及桓仁所做的点火实验所得数据为林火蔓延的实测值[16],与此次改进模型的计算值进行比对。参数为可燃物修正系数Ks=1.1,坡度w=15°,坡向南,风速 v=1m/s,风向 NW,θ=315°。 于良成等人给出的初始蔓延速度R0=0.36m/min,而本文经过使用可燃物湿度m=18.6%计算,得到初始蔓延速度R0=0.359m/min,与于良成估算的初始蔓延速度极其接近,然后使用改进的坡度修正系数Kφ进行计算,得到林火蔓延速度计算对比结果如表6。

表6 实测值、改进前与改进后计算值对比表Table 6 Comparison of measured values,preimprovement and improved calculated values
显而易见,改进后的林火火峰蔓延速度模型比改进前的计算值更接近实测值。
由于风方向和上坡方向都对林火的蔓延起到促进作用[17],本文分两种情况使燃烧试验更具直观性,并使用下列两图对模型结果进行可视化展示。图4为风方向与上坡基本处于同一方向,林火蔓延30min后各个方向的蔓延情况。图5为风方向与上坡基本处于相反方向,林火蔓延30min后各个方向的蔓延情况。
4 结论与讨论
通过对林火蔓延速度的研究,得到以下几点结论:
(1)林火蔓延的初蔓延始速度对于林火行为的预测,是一个非常重要的因素。而影响初始蔓延速度的因素有很多,本文针对可燃物湿度对初始蔓延速度的影响做出了研究,模型相关系数达到0.9201,说明可燃物湿度对林火初始蔓延速度的影响很大,可以作为预估初始蔓延速度的一个重要因素。
(2)坡度和坡向是影响林火蔓延速度和方向的重要因素,即地形与风因素相结合下可以得到多种不同的情况,不能仅仅局限于几个方向的研究,要理论联系实际,从实验中总结经验,对林火蔓延行为的研究有重要意义。
本文的改进模型,使初始蔓延速度的计算和坡度修正系数的计算更加准确快速,从而使林火蔓延速度的预估结果也更加准确,对做好森林灭火决策,最大限度地减少森林火灾造成的损失,具有重要的作用。

