基于自适应遗传算法的弹道性能优化设计*
王睦深,谭湘霞
(北京电子工程总体研究所,北京 100854)
0 引言
飞行空域是导弹武器系统的一个重要作战综合性能指标[1]。高界、低界、远界和近界是垂直平面内飞行空域参数中的几个主要参数,其中命中点位于低界和远界交点的弹道称为低远弹道,是导弹所有工作状态中对大气层内稳定控制性能要求最高的一种情况。以往的方法是将飞行过程按时序分割成几个阶段,然后分段设计优化,忽略了各阶段之间的相互影响。本文以某第三级包含2个脉冲的三级导弹为例,采用自适应遗传算法,将常温低远弹道作为一个典型工况,对其性能进行整体优化。
1 动力学模型
本文将导弹视为变质量质点系,地球模型使用旋转总地球椭球体模型,大气模型采用标准大气模型,在弹体系和发射惯性坐标系下,进行质心动力学模型的建立和求解。
变质量质点系在惯性坐标系下的质心动力学矢量方程为[2]
(1)

附加哥氏力矢量的表达式为
(2)

导弹的受力分析在弹体系下进行[3],通过坐标变换,将作用在导弹上的力变换至发射惯性坐标系进行积分运算。
本文还对导弹所受突风进行了建模[4-7],仿真过程中考虑了风场附加攻角对导弹飞行的影响。
2 优化模型
2.1 优化变量
本文的优化问题为不引入目标模型的开环弹道参数优化模型,因此为了对飞行空域进行优化,需要对飞行过程中各级飞行程序和飞行时序进行设计。
(1) 一级飞行程序
一级飞行程序以攻角作为控制变量,采用解析的经验关系式生成飞行程序,飞行程序如下:
(3)
(4)
(5)
式中:t11为亚声速段开始攻角转弯时刻;t12为亚声速段结束攻角转弯时刻;αm为亚声速段上攻角绝对值的最大值;tm为攻角达到最大值的时间,π为圆周率。
假设导弹发射后,进行几秒的垂直上升稳定飞行后开始攻角转弯。
理论上,当导弹达到跨声速段时,导弹的飞行稳定性较差,攻角越小越好[8]。
综上,一级飞行程序中的t11时刻前,导弹完成垂直上升稳定飞行,t12时刻后,导弹进入跨声速段(Ma>0.8),此时攻角必须减小接近于0,因此攻角必然在t11,t12之间达到极大值,即:
tm∈[t11,t12].
由弹道初步仿真结果,导弹的可用攻角有很大余量,但由于受到一级分离点高度等条件的限制,导弹不能在一级飞行过程中进行较大攻角的转弯,需用攻角事实上远小于可用攻角,因此人为设定αm的上界αup以缩小优化变量范围,提升优化算法求解速度:
αm∈[0,αup].
(2) 二级飞行程序
二级飞行程序采用俯仰角程序,在二级飞行稳定后,使俯仰角线性下降一定时间,然后保持常值,直至二级飞行结束。
假设t21时二级飞行达到稳定,开始进行转弯,俯仰角指令线性下降,于t22时刻停止下降,保持常值,二级飞行程序表达式为
(6)
ak为俯仰角直线下降斜率,设其最大不超过aup,则取值范围为
ak∈[0,aup].
(3) 三级飞行程序
三级程序采用俯仰角程序,设一脉冲和二脉冲的俯仰角程序均保持常值,分别为φ31和φ32,即
(7)
式中:φ31为一脉冲作用时的俯仰角;φ32为二脉冲作用时的俯仰角,无量纲取值范围均设为0~1。
(4) 飞行时序
导弹的飞行空域与其飞行时序有关,其中,设一级关机后、一级分离前的滑行时间为Tc1;一级分离后、二级开机前的滑行时间为Tc2;二级分离后,三级一脉冲开机前的滑行时间为Tc30;三级一脉冲关机后,三级二脉冲开机前的滑行时间为Tc31。
由于一级关机后,二级开机前,导弹处于大气层内且无姿态控制能力,因此不进行滑行,三级处于大气层外,可以滑行。
时序变量的表达式为
(8)
综上,全部优化变量如下:
式中:t3=1.187;f4=1;t5=0.396;f6=1。
2.2 目标函数
本文对低和远2个矛盾的指标进行优化,因此使用加权法对二者进行结合,得到其优化目标函数为
maxJ=λR+(1-λ)(15 000 000-H),
(9)
式中:高度指标H通过构造减法的形式,得到与航程指标R数量级一致的极大值指标;λ为权重系数,二者加权结合后形成极大值指标J。
2.3 约束条件
本文考虑的约束条件包括可用攻角约束、可用过载约束、分离点动压约束、最终点弹道倾角约束[9-10],其表达式为
(10)
式中:α(t)为t时刻需用攻角;n(t)为t时刻需用过载;αmax(t)为t时刻可用攻角;nmax(t)为t时刻可用过载;qsep12为一、二级分离点动压;Q为一、二级分离点动压值上限;θf为最终点的弹道倾角;ω为导引头视场角。
2.4 优化方法
优化方法使用自适应遗传算法[11-13],约束条件使用罚函数法处理。
优化变量由于个数较多,采用二进制编码时,若要保证结果的计算精度,需要很长的基因长度,因此本文对优化变量直接采用实数编码的方式[14-15]。
交叉概率Pc和变异概率Pm的自适应方法如下:
(11)
(12)
式中:[Pc2,Pc1]为交叉概率取值范围;[Pm2,Pm1]为变异概率取值范围;fc为交叉的2个个体适应度中较大的适应度;fm为要变异个体的适应度值;favg为每代群体的平均适应度值;fmax为每代群体中最大适应度值。
由于本文所求极值为极大值,且所有适应度值均为正值,直接对不符合约束条件的适应度值进行一定程度的缩小即可有效排除不符合约束条件的个体,处理约束条件的罚函数法表达式为
Jcost=c·J,
(13)
式中:J为适应度值;Jcost为考虑了惩罚的适应度值;c为对适应度值进行放缩时的比例系数。
3 仿真计算结果分析
仿真计算基于自适应遗传算法对弹道进行整体优化,并与已有的分段优化结果相比较,已有分段优化的三级双脉冲采用数值相等的俯仰角指令设计。
对导弹进行整体优化的遗传算法设置为种群规模100,进化代数200,目标函数权重系数设为0.5,适应度放缩比例系数符合约束条件时取为1,不符合约束条件时取为0.001,交叉概率取值范围设为[0.4,0.9],变异概率的取值范围设为[0.001,0.4]。进行无量纲化处理后,优化结果如表1所示。
整体优化结果与分段优化结果在特征点处的无量纲参数对比如表2所示。表2中,t1代表一级分离点,t2代表二级分离点,t9代表三级分离点。
优化后弹道的无量纲航程-海拔曲线如图1所示。
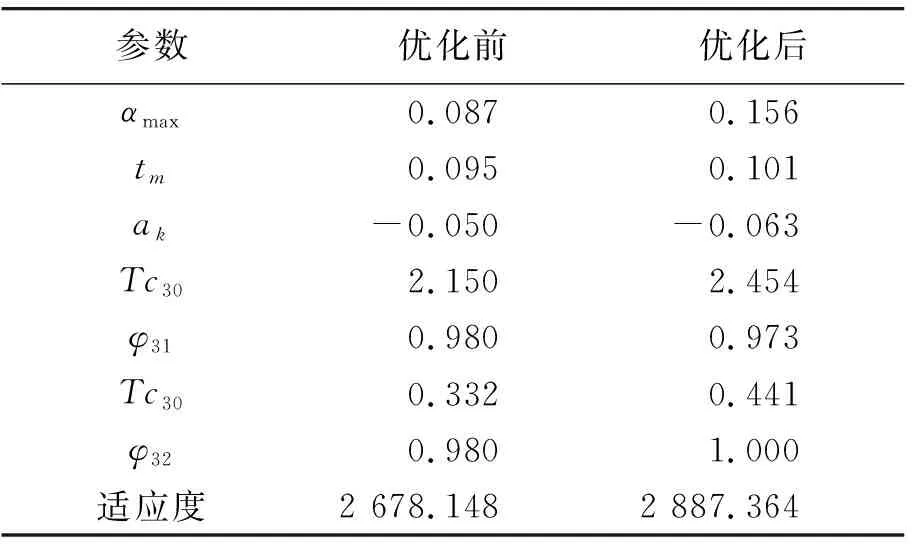
表1 优化结果Table 1 Optimization Results
注:表1中各量均为相对量
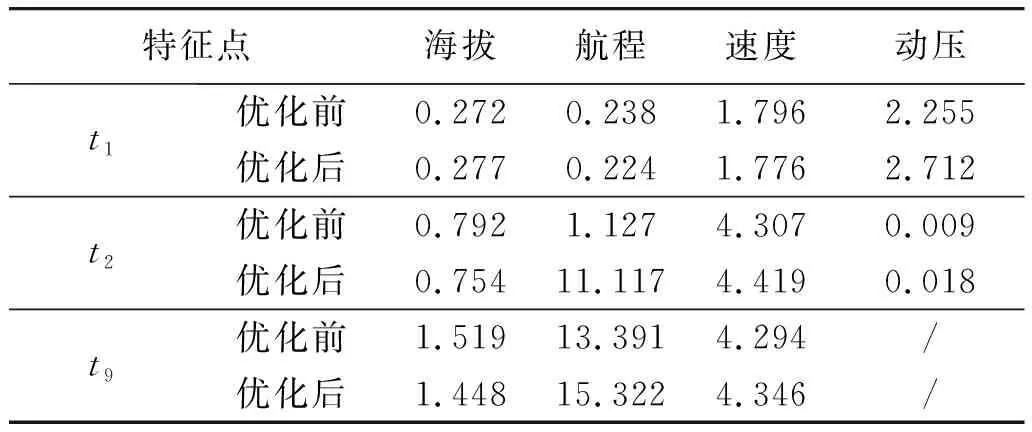
表2 优化前后参数对比表Table 2 Parameter comparison before and after optimization
注:表2中各量均为相对量

图1 优化结果曲线Fig.1 Image of optimization result
由表2和图1可以看出优化后的结果在保证最后处于上升段命中的条件下,比优化前海拔低4.7%、地面航程远14.42%,导弹的低远射界得到了进一步扩大。
整体优化后,导弹在一级和二级的下压程度比分段优化得到结果的下压程度小,弹道的抛物线部分更高,并通过三级滑行时间的增长和三级俯仰角程序的重新设计及优化,得到了性能更好的弹道,而且优化后一级分离时的动压减小9.73%,有利于导弹分离时的稳定,优化后t9时刻的导弹速度提高了1.2%,有利于提高杀伤效果。
4 结束语
本文对导弹进行了动力学建模,对导弹的飞行程序和时序进行了设计,对优化问题的目标函数和约束条件进行了设计,最终使用自适应遗传算法对常温低远弹道参数优化问题进行了求解,得到的优化结果相对于以往优化方法得到的结果海拔更低、航程更远,性能更好。

