偏载作用下单箱三室波形钢腹板悬臂梁的力学特性
周东波1,邓文琴,刘 朵3,张建东
(1.宁波市鄞州区交通投资有限公司,浙江 宁波 330200; 2.华中科技大学 土木工程与力学学院,湖北 武汉 430074; 3.河海大学 土木学院,江苏 南京 210024; 4.南京工业大学 土木工程学院,江苏 南京 211800)
波形钢腹板组合箱梁因其自重轻、抗震性能优、预应力效率高等优势,在国内外桥梁工程中得到了广泛的应用[1-3]。为满足日益增长的交通梁需求,桥梁逐步向大跨度发展,单箱多室箱形截面形式被广泛采用[4-5]。目前大跨径波形钢腹板组合梁桥一般采用对称悬臂施工[6-7],相比成桥状态,单箱多室波形钢腹板悬臂施工期稳定性较弱,且施工过程中不对称荷载因素较多,偏载产生的空间力学性能更加明显。
李宏江等[8]、郑尚敏等[9]、王保圣[10]、陈宜言等[11]对单箱单室波形钢腹板扭转与畸变性能、扭转振动特性、抗扭性能进行了模型试验和理论分析,得到了该类截面翘曲应力分布特征及影响因素,并提出了扭转与畸变计算方法。刘保东等[12]研究了内衬混凝土对波形钢腹板刚构桥扭转和畸变性能的影响,马磊等[4]基于模型试验推导了单箱双室波形钢腹板简支梁扭转与畸变计算公式,并分析了宽跨比等几何参数截面抗扭性能的影响。上述研究主要针对单箱单室简支梁体系或连续梁体系,但针对单箱多室箱梁及悬臂体系偏载作用下梁体空间力学性能的研究很少,与简支梁或连续梁相比,施工期悬臂状态下梁体受力更为复杂,不对称荷载因素较多,偏载作用下截面空间效应更加显著。
基于此,本文通过模型试验研究了悬臂状态下单箱三室波形钢腹板组合箱梁在偏载作用下,截面因扭转产生的翘曲应力及附加剪应力等力学特性,为单箱三室波形钢腹板组合箱梁悬臂施工期截面翘曲应力的计算提供依据。
1 模型试验
1.1 试验设计
试验模型为等截面双悬臂梁,总长426 cm,单侧悬臂长度为168 cm。截面形式为单箱三室波形钢腹板组合箱梁,梁高84 cm,顶板宽230 cm,底板宽180 cm,顶底板厚度均为12 cm,波形钢腹板厚度为3.75 mm,模型具体构造尺寸如图1所示。试验梁所用混凝土为C60,实测抗压强度为72.6 MPa,弹性模量为49.3 GPa,泊松比为0.2,波形钢腹板采用Q345钢,弹性模量为210 GPa,泊松比为0.3。
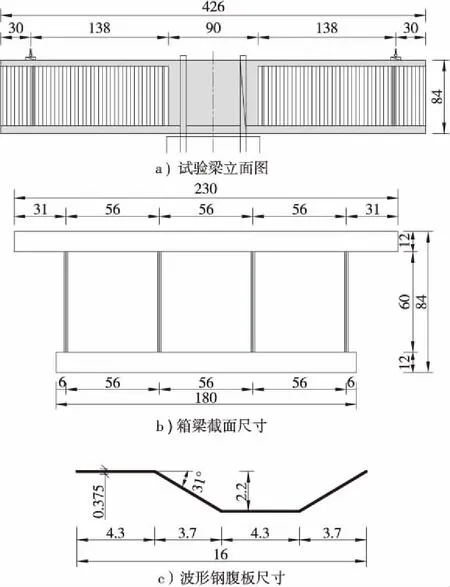
图1 试验梁尺寸构造图(单位:cm)Figure 1 Dimension of specimen (Unit:cm)
1.2 加载方式
试验采用4台千斤顶串联加载,荷载作用于距两侧悬臂端30 cm处,加载点位于4道腹板上方,分别进行对称加载和偏心加载,如图2所示。加载共分为4级,每40 kN一级,每级加载稳定5 min后读数。
1.3 测点布置
试验测试内容包括梁体变形、混凝土板应变和钢腹板应变,两侧悬臂端部均在4道腹板对应底板位置各布置4个位移计,在A、B截面处布置应变测点,其中波形钢腹板沿高度方向布置3个应变花测点,顶底板沿横向布置纵向应变测点,测点布置如图3所示。

(a)试验加载装置
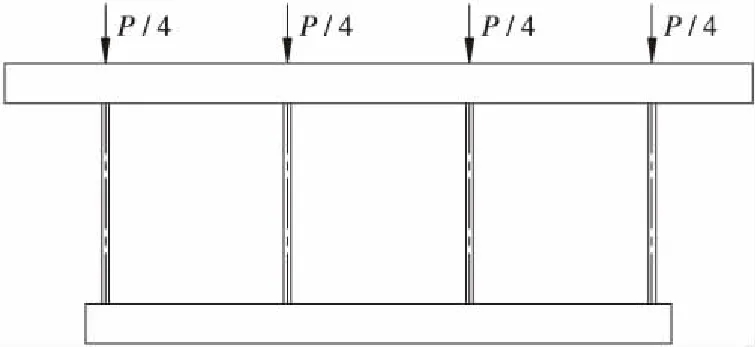
(b)对称加载
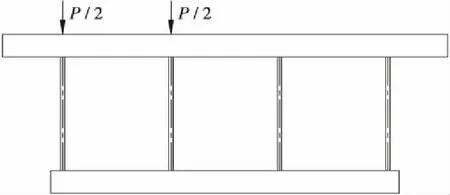
(c)偏心加载图2 加载方式Figure 2 Loading method
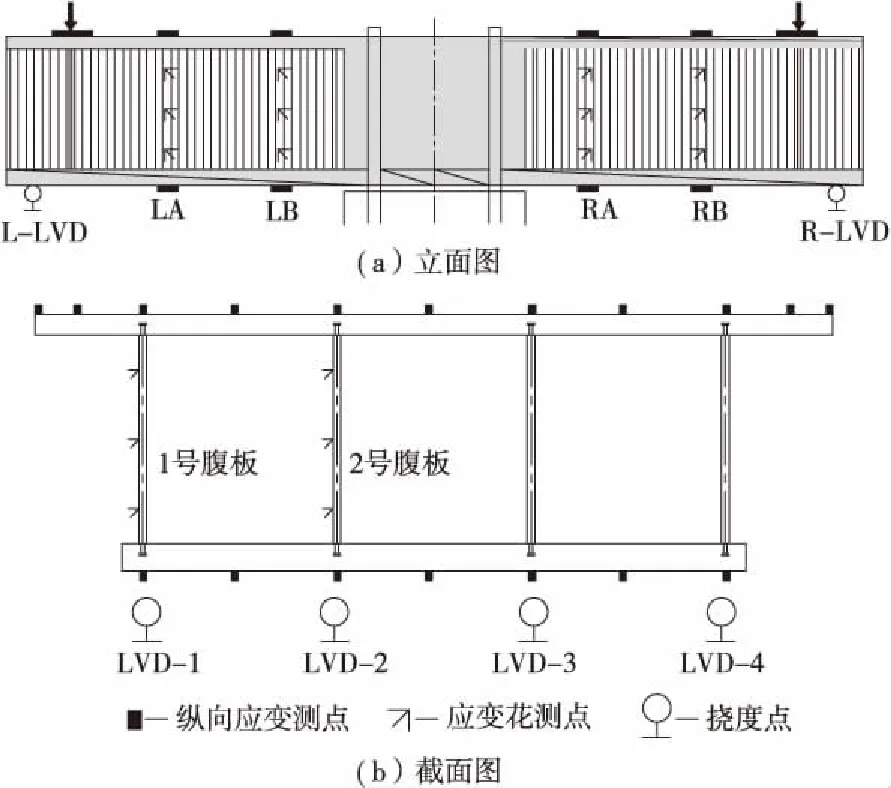
图3 测点布置图Figure 3 Layout of measurement points
2 试验结果与分析
2.1 挠度
表1列出了各级荷载作用下试验梁悬臂端截面的挠度实测值,由表1可知,在相同荷载工况下,偏载加载侧产生的挠度值均大于对称荷载产生的挠度值,其比值为1.23~1.32;远离加载侧最外侧腹板偏载产生的挠度值稍小于对称加载,其比值为0.83~0.85,因此,偏载作用下角点位移在设计计算中不容忽视。
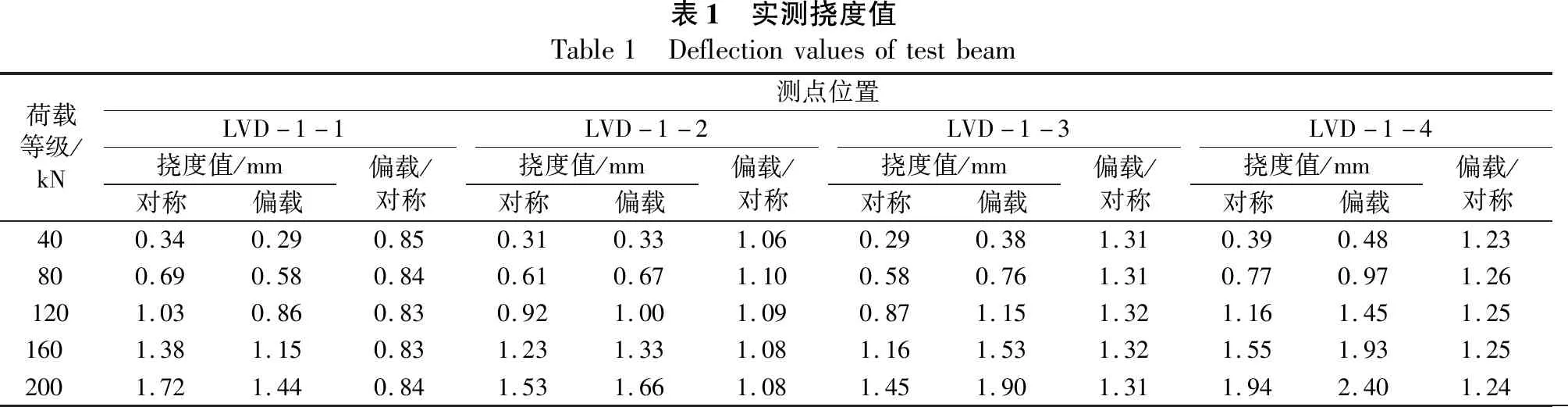
表1 实测挠度值Table1 Deflectionvaluesoftestbeam荷载等级/kN测点位置LVD-1-1LVD-1-2LVD-1-3LVD-1-4挠度值/mm对称偏载偏载/对称挠度值/mm对称偏载偏载/对称挠度值/mm对称偏载偏载/对称挠度值/mm对称偏载偏载/对称400.340.290.850.310.331.060.290.381.310.390.481.23800.690.580.840.610.671.100.580.761.310.770.971.261201.030.860.830.921.001.090.871.151.321.161.451.251601.381.150.831.231.331.081.161.531.321.551.931.252001.721.440.841.531.661.081.451.901.311.942.401.24
2.2 纵向翘曲正应力
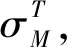
(1)
a.钢板翘曲正应变。
偏心荷载作用下,截面纵向翘曲正应变可通过式(1)求得,A、B截面边腹板和中腹板纵向翘曲正应变分布如图4所示。从图4中可以看出,由于波形钢腹板存在手风琴效应,腹板沿纵向可伸缩,在对称荷载及偏心荷载作用下,腹板上纵向正应变明显小于顶底板。A截面顶底板翘曲应变相差不大,B截面底板翘曲应变明显大于顶板,且各截面底板翘曲正应变随荷载增加呈线性增大,而腹板的翘曲正应变相对于顶、底板而言较小。
b.混凝土板翘曲正应力。
图5给出了截面纵向翘曲正应力沿横截面的分布趋势,由图5可知,混凝土顶、底板翘曲正应力随荷载增加基本呈线性增长,顶板最大翘曲应力出现在悬臂翼缘板处,底板最大翘曲应力出现在底板边腹板角点处,底板翘曲应力稍大于顶板,截面最大翘曲应力出现在底板角点处。表2给出了偏心荷载作用下混凝土板最大翘曲正应力与弯曲正应力比值,由表2可知,A截面顶板最大翘曲正应力约为弯曲正应力的1.3倍,底板最大翘曲正应力约为弯曲正应力的1.5倍,B截面顶板最大翘曲正应力约为弯曲正应力的1.3倍,底板最大翘曲正应力约为弯曲正应力的1.2倍,由此可知,波形钢腹板组合截面偏心荷载作用下截面翘曲正应力对截面应力影响较大,应给予重视。另外还可看出,B截面顶、底板翘曲正应力大于A截面,说明对于等截面悬臂梁而言,截面翘曲应力由悬臂端向墩顶锚固端逐渐增加。
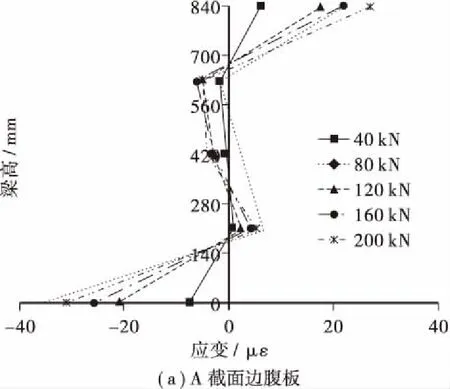
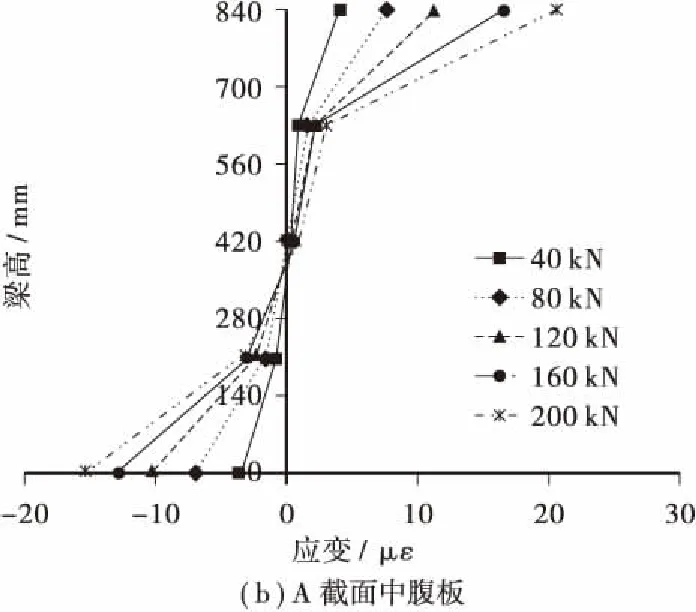
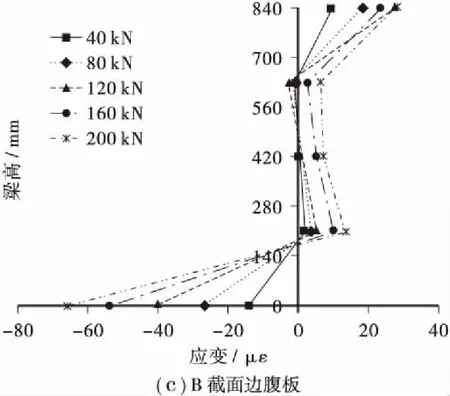
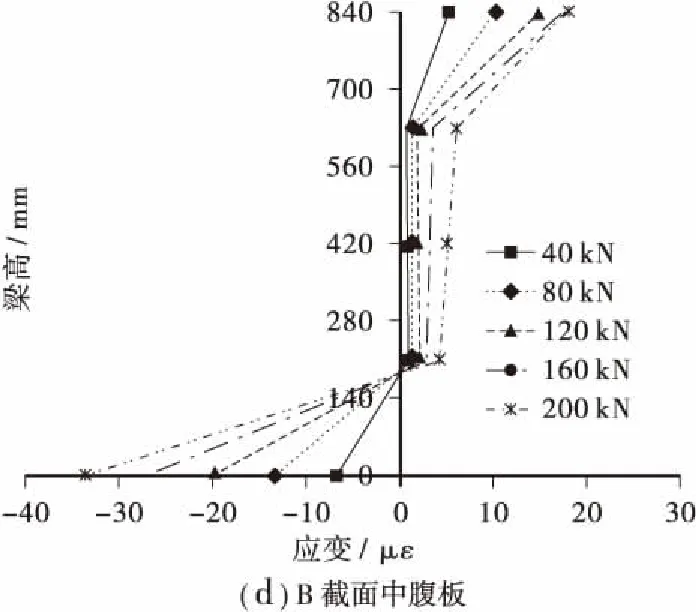
图4 翘曲正应变沿梁高分布Figure 4 Distribution of warping normal strain along the height of girder
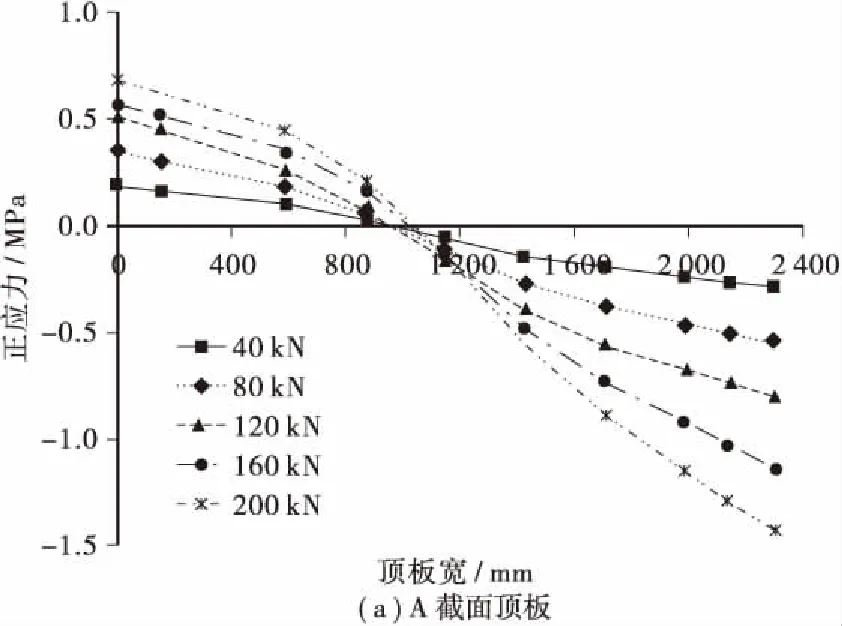
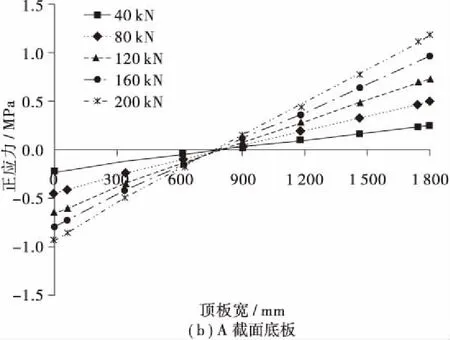
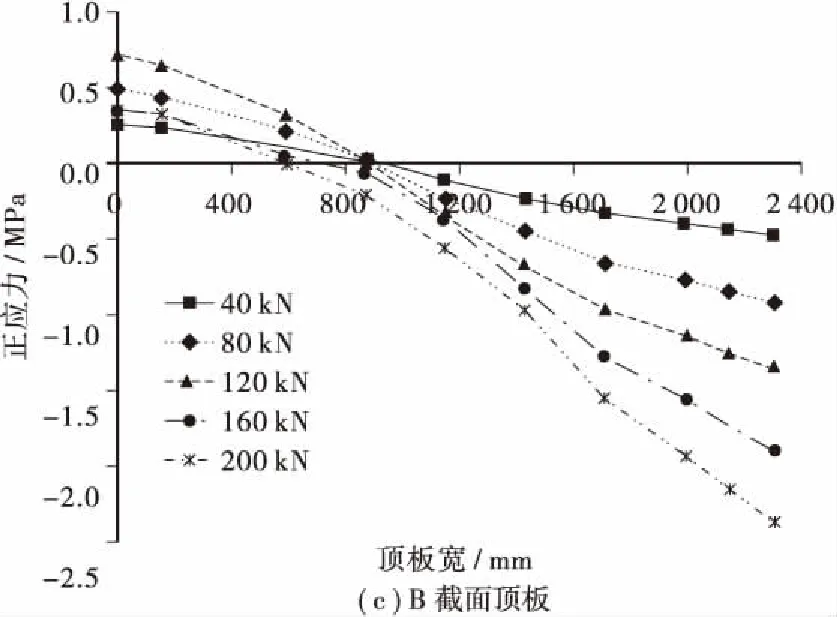
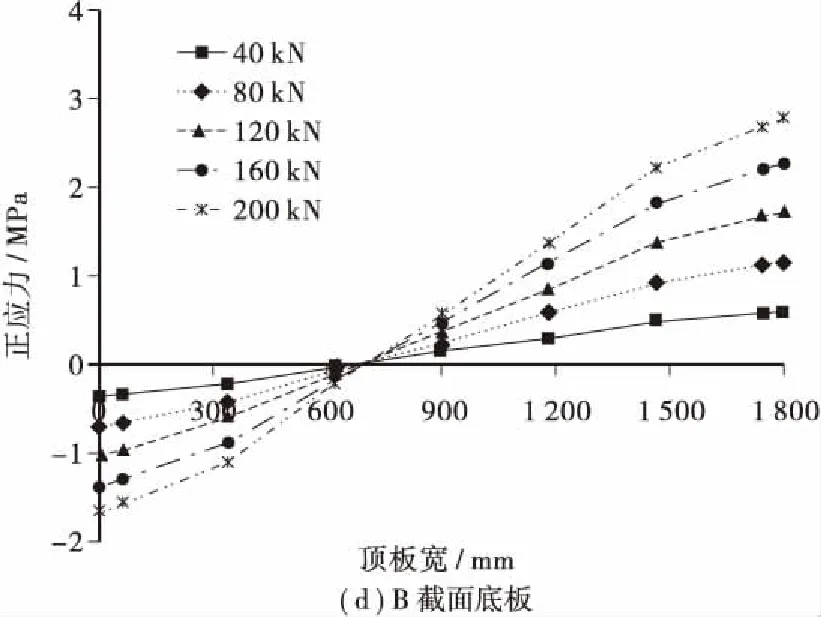
图5 混凝土板纵向翘曲正应力横向分布Figure .5 Distribution of warping normal stress of the concrete slabs along the transverse direction
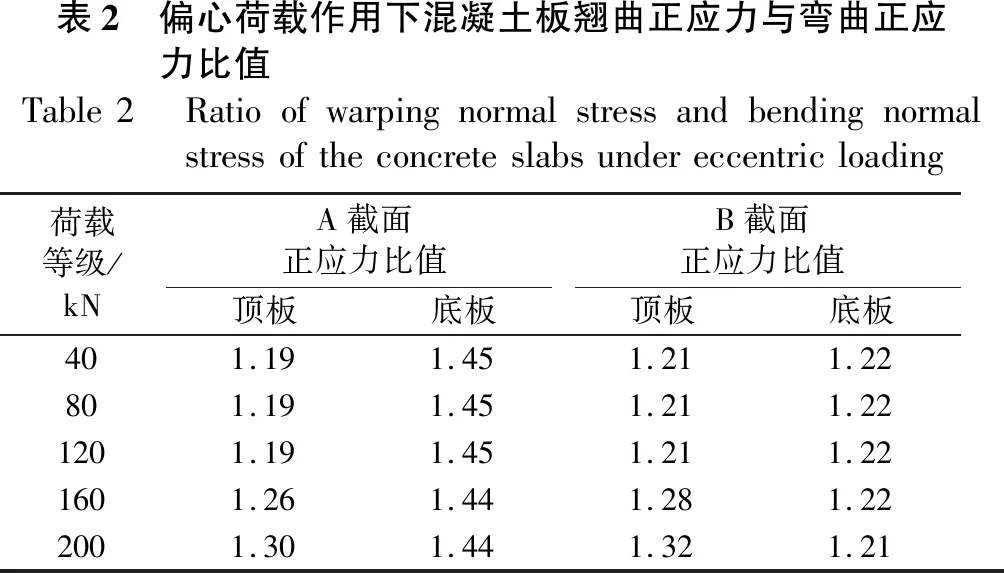
表2 偏心荷载作用下混凝土板翘曲正应力与弯曲正应力比值Table2 Ratioofwarpingnormalstressandbendingnormalstressoftheconcreteslabsundereccentricloading荷载等级/kNA截面正应力比值顶板底板B截面正应力比值顶板底板401.191.451.211.22801.191.451.211.221201.191.451.211.221601.261.441.281.222001.301.441.321.21
2.3 钢腹板附加剪应力
(2)
偏心荷载作用下,腹板附加剪应力可由式(2)求得,图6给出了各荷载工况下腹板附加剪应力沿高度方向的分布图,从图6中可以看出,腹板附加剪应力沿梁高方向也基本呈等值分布,同一截面,加载侧边腹板附加应力值明显大于中腹板,由此可知,对于单箱多室波形钢腹板组合箱梁而言,偏心荷载作用下,加载侧边腹板产生的附加剪应力最大,设计时可选取边腹板进行计算分析。
表3给出了偏心荷载作用下腹板附加剪应力与弯曲剪应力比值,从表中可以看出,对称荷载作用下,A截面边腹板产生的附加剪应力较大,约为弯曲剪应力的1.10~1.21倍,中腹板附加剪应力占弯曲剪应力比值相对较小,约为0.51~0.55倍;B截面边腹板附加剪应力约为弯曲剪应力1.23~1.34倍,中腹板附加剪应力约占弯曲剪应力0.55~0.64倍。对比A、B截面可知,针对单箱多室等截面悬臂梁而言,越靠近墩顶截面,附加剪应力越明显。
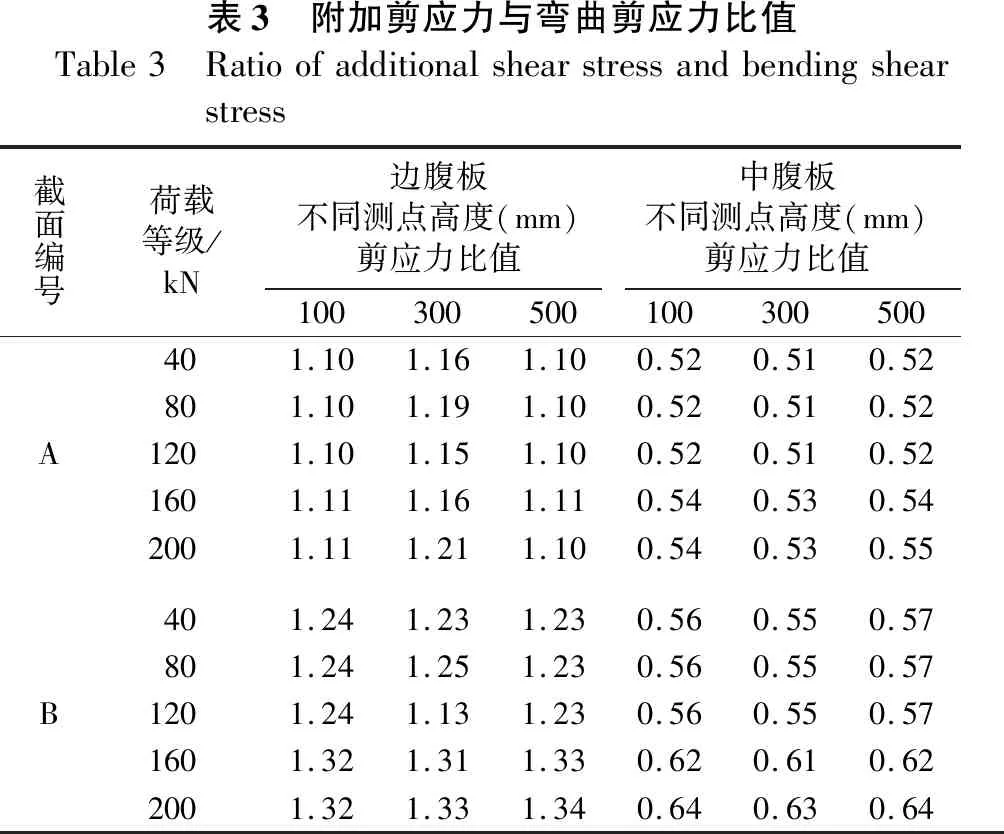
表3 附加剪应力与弯曲剪应力比值Table3 Ratioofadditionalshearstressandbendingshearstress截面编号荷载等级/kN边腹板不同测点高度(mm)剪应力比值中腹板不同测点高度(mm)剪应力比值100300500100300500401.101.161.100.520.510.52801.101.191.100.520.510.52A1201.101.151.100.520.510.521601.111.161.110.540.530.542001.111.211.100.540.530.55401.241.231.230.560.550.57801.241.251.230.560.550.57B1201.241.131.230.560.550.571601.321.311.330.620.610.622001.321.331.340.640.630.64
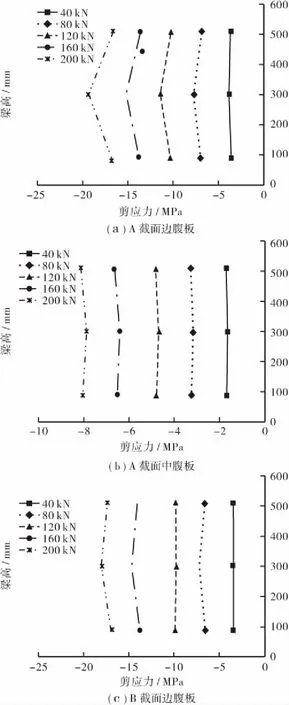
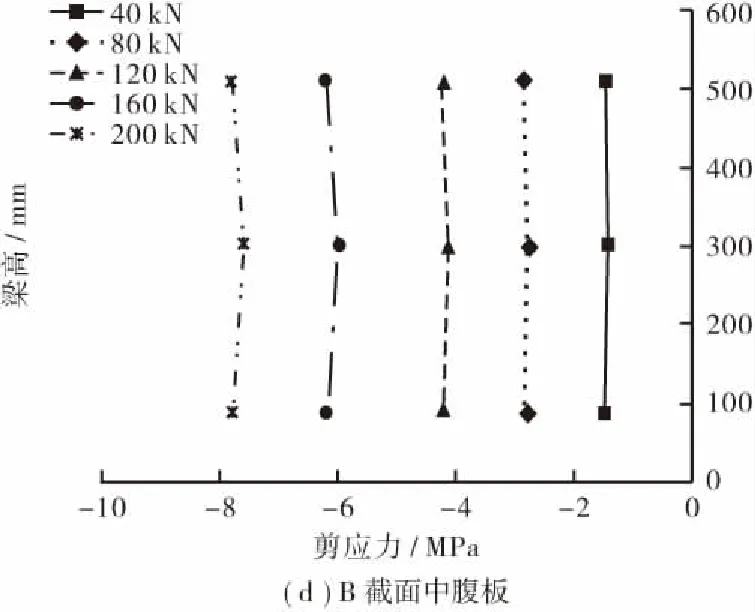
图6 腹板附加剪应力沿高度方向的分布Figure 6 Distribution of additional shear stress along the height of the corrugated steel webs
3 某实桥有限元分析
3.1 工程概况
为研究实际工程中单箱三室波形钢腹板悬臂施工期偏载作用下力学性能,以某三跨单箱三室波形钢腹板组合梁连续梁桥为研究对象,其跨径及截面构造如图7所示。
3.2 有限元模型建立
采用三维有限元实体分析软件建立大桥最大悬臂施工阶段有限元模型,最大悬臂施工共划分为16个节段,混凝土部分均采用3D实体单元进行模拟,波形钢腹板采用2D壳单元模型,预应力筋采用1D杆系单元进行模拟,波形钢腹板单元与混凝土单元通过共节点的方式进行处理,模型如图2所示。
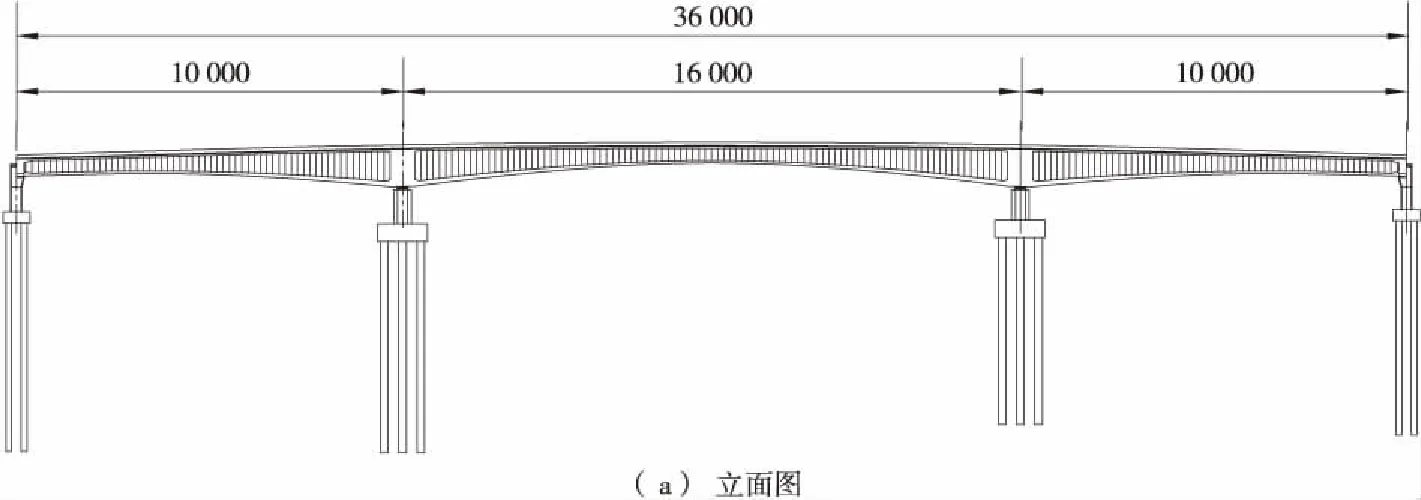
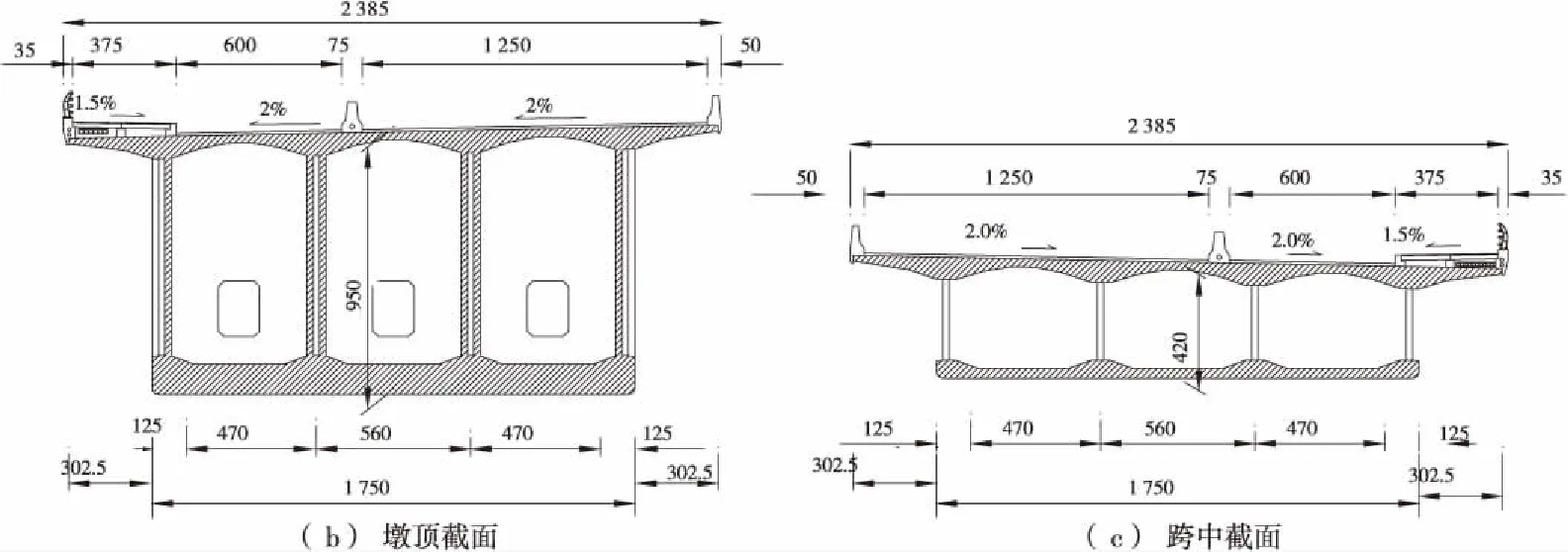
图7 某波形钢腹板连续梁桥结构布置 (单位:cm)Figure 7 Structural arrangement of a continuous girder bridge with corrugated steel webs( Unit:cm)

图8 最大悬臂阶段有限元模型Figure 8 Finite element model of the maximum cantilever stage
3.3 加载工况
为分析单箱三室波形钢腹板组合梁截面偏心荷载作用下施工期的力学性能,分别进行2组工况分析。CASE 1为仅考虑偏载作用,即60 t(取挂篮荷载的一半)荷载作用于最大悬臂节段两端;CASE 2为考虑恒载(自重+预应力)+偏载作用。为避免集中力作用影响,选取15节段靠近墩顶侧截面进行分析,加载工况如图9所示。
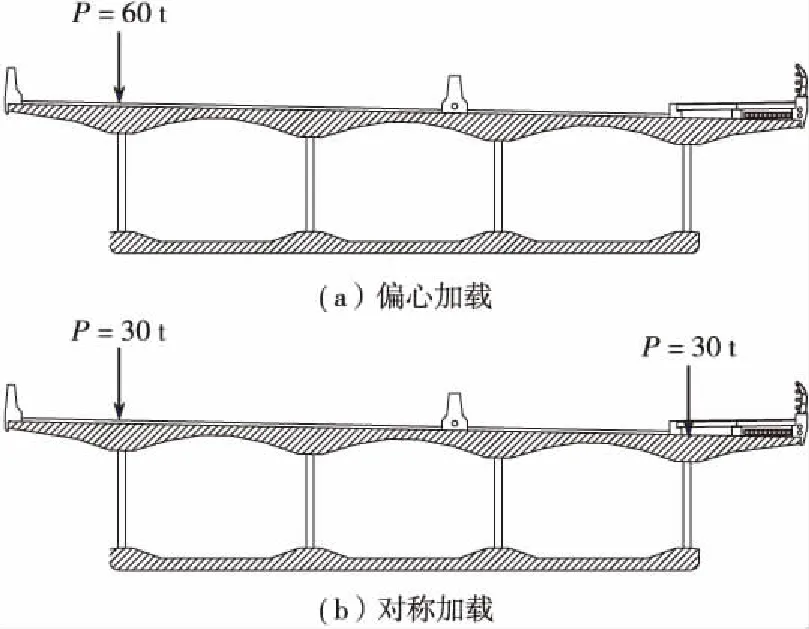
图9 加载位置Figure 9 Loading position
3.4 最大悬臂阶段扭转与畸变性能分析
CASE 1和CASE 2工况作用下截面顶、底板翘曲应力与弯曲应力比值分别如图10、图11所示。由图10可知,仅考虑偏载作用是,截面顶板最大翘曲应力与弯曲应力比值为110.0%,底板最大翘曲应力与弯曲应力比值为125.8%,结果与缩尺模型试验结果相差不大。由于梁体弯曲应力大部分由结构自重引起,试验结果仅反映偏载作用下截面翘曲应力结果,其翘曲应力影响比值会被放大,其结果仅可定性反映翘曲应力的影响,但其具体比值不具有工程参考价值。由图11可知,考虑恒荷载作用时,截面顶板最大翘曲应力与弯曲应力比值为10.0%,底板最大翘曲应力与弯曲应力比值为20.4%,而考虑恒载作用时,偏载作用下截面翘曲应力与弯曲应力比值明显小于不考虑恒载作用时,但底板翘曲应力仍占弯曲应力20%左右,因此实际工程悬臂施工过程中不可忽视偏载引起的翘曲应力产生的影响。
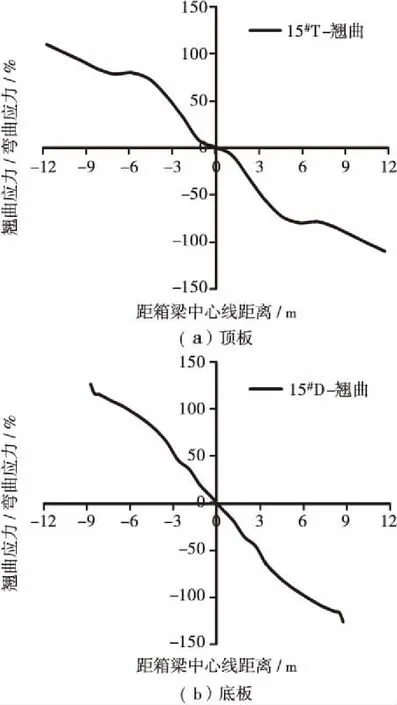
图10 CASE 1作用下混凝土板翘曲应力与弯曲应力比值Figure 10 Ratio of warping normal stress and bending normal stress under the loading of CASE 1
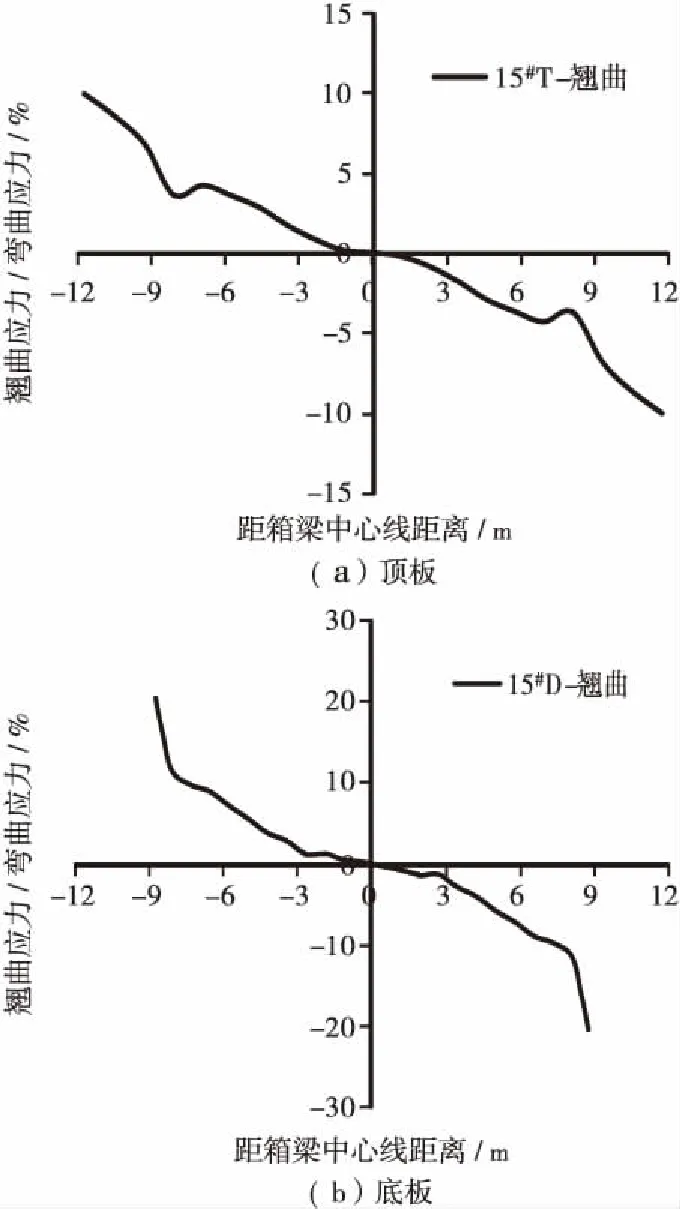
图11 CASE 2作用下混凝土板翘曲应力与弯曲应力比值Figure 11 Ratio of warping normal stress and bending normal stress under the loading of CASE 2
4 结论
a.由于波形钢腹板存在手风琴效应,在对称荷载及偏心荷载作用下,腹板上纵向正应变明显小于顶底板,可忽略不计。
b.偏载作用下,混凝土板最大翘曲应力出现在底板角点处,腹板附加剪应力沿梁高方向呈等值分布,同一截面,加载侧边腹板附加应力值明显大于中腹板,故单箱多室波形钢腹板组合梁设计时,应考虑混凝土板翘曲应力的影响,且可选取边腹板进行翘曲应力计算分析。
c.由于梁体弯曲应力大部分由结构自重引起,考虑恒载作用时,偏载作用下截面翘曲应力与弯曲应力比值明显小于不考虑恒载作用时,但底板翘曲应力仍占弯曲应力20%左右,因此实际工程悬臂施工过程中不可忽视偏载引起翘曲应力产生影响。

