基于ANN的岩土体热阻系数预测模型研究
张 涛, 王才进, 刘松玉, 段隆臣
(1.中国地质大学 工程学院, 湖北 武汉 430074; 2.东南大学 岩土工程研究所, 江苏 南京 210096)
建筑材料的热学特性测试与分析是当前土木工程领域研究的热门课题之一,准确、有效地测定土体的热导率/热阻系数是各类构筑物温度场分析和能源建筑设计的重要内容[1-3].低温地区建筑地基与道路基础的冻土融沉、地下管线和核废料处置场地的设计、地下热能的存储与利用和能源桩设计等工程实践问题均与土体的热物理性质密切相关[4-6].土的热物理性质参数主要有热阻系数Rt(热导率k的倒数)、热扩散系数α和比热容(包括质量比热容和体积比热容),其中热阻系数对于稳态传热过程中土体的温度场分布有着决定性的影响,需要进行系统、深入的研究[7].一般的,土是由固、液、气三相介质组成的复杂建筑材料,其热阻系数主要由三相介质内部和介质之间的热能传递组成,同时受到多个因素的影响,如固体颗粒矿物成分、干密度、颗粒级配与形态、时间和温度等[8].因此,深入了解土体的热传导特性和准确获得其热阻系数对于建筑热工结构的设计与应用有着重要的实践指导意义.
现有学者对土体热传导特性与计算模型进行了大量研究.Naidu等[9]利用非稳态热探针对印度地区多种类型土体的热阻系数进行了室内测试,分析了含水量和干密度等参数对这些土体热阻系数的影响规律.Barry-Macaulay等[10]采用分隔平板装置对澳大利亚地区岩石材料的热导率进行了测试,并探讨了矿物成分和各向异性对岩石传热性能的影响.Zhang等[11]在利用热-时域反射探针测试ASTM标准砂热阻系数的基础上,提出了一个砂土热阻系数的经验关系模型.现有关于土体热阻系数的计算模型大体可分为经验模型和半经验理论模型2类.经验模型是借用数学统计方法对土体热阻系数的测试结果进行回归分析,建立土体热阻系数与含水量、干密度、孔隙率和饱和度等影响因素之间的数学关系式;半经验理论模型常在经典热传导理论基础上,通过简化岩土材料的热传递过程,最终形成土体热阻系数的理论模型[12-13].从严格意义上说,半经验理论模型实质上亦是一种经验模型.现有研究结果表明,大多热阻系数预测模型的计算精度因土体类型、赋存状态的差异而低于设计要求,难以推广应用.因此,土木工程师们亟需寻求一种简单、准确估算土体热阻系数的新模型.
为建立准确预测土体热阻系数的计算模型,本文首先简要分析了影响土体热阻系数的主要因素,然后利用人工神经网络(artificial neural network,ANN)方法,提出了预测土体热阻系数的单一模型(2个输入参数)和广义模型(4个输入参数),并与传统经验关系模型相对比,验证了本文模型的有效性和优越性.研究内容可为岩土体热阻系数的预测提供新的途径,同时,对其他建筑材料工程性质指标的估算也具有一定借鉴意义.
1 岩土体热传导特性
笔者曾利用非稳态热探针对多种类型土体的热阻系数进行了测试,得到了土体热阻系数Rt与含水量ww、干密度γd的相互关系,如图1所示[14].显然,增加含水量可使土体热阻系数逐渐降低,并远小于其在干燥状态下的值.水分不仅可以排挤出孔隙中的空气,还可以包裹固体颗粒,在其表面形成水膜,同时可使固体颗粒间产生“水桥”,有利于热量的传递.当水分占据土体孔隙中绝大部分空间时,颗粒表面水膜和水桥形成完全,此时热量的传递仅发生于固、液两相介质内部和两相之间[15],热阻系数表现为最小[16].土体三相介质中,固体颗粒的导热能力显著优于其他两相介质,且颗粒接触特性改善亦可提高土体的传热能力,降低热阻系数.因此,相同条件下,增加干密度可使土体热阻系数有所降低.图1中黏土和砂土的热阻系数随干密度的变化均符合上述规律.
矿物成分对固体颗粒的导热性能有着决定性的影响.Cote等[17]指出常见岩土体的矿物成分中,石英的热阻系数(约13K·cm/W)最低,泥炭的热阻系数(约400K·cm/W)最高.估算土颗粒热阻系数常采用Johansen[18]提出的“几何平均法”,其中石英含量是非常重要的计算参数之一.图1中的黏土和细砂在含水量和干密度相差不大时,其热阻系数却相差很大.这一显著差异主要是土颗粒矿物成分不同所引起.颗粒粒径分布与形态对土体热传导性能亦有一定影响,此影响主要归因于颗粒间接触数量的变化[19-22].单位体积土体的颗粒接触数目随其粒径减小而增加,然而,因颗粒间的接触热阻显著高于颗粒内部的热阻,致使热量在土体中的传递变得困难,热阻系数增加.这也在某种程度上阐释了图1中砂性土热阻系数小于黏性土的原因.温度改变会影响材料分子的热运动,进而影响材料的热传导性能.一般情况下,升温引起的材料分子、原子热运动加剧有利于热量的传递,降低土体的热阻系数[23].天然岩土材料均具有各向异性特点,现有少数学者研究了各项异性对岩石传热性能的影响,一般以热量传递方向与节理面的夹角为研究对象,分析热阻系数随夹角的变化规律[10,24].由于细粒土的各向异性难以定量描述,目前关于其对细粒土导热性能的影响鲜有报道.
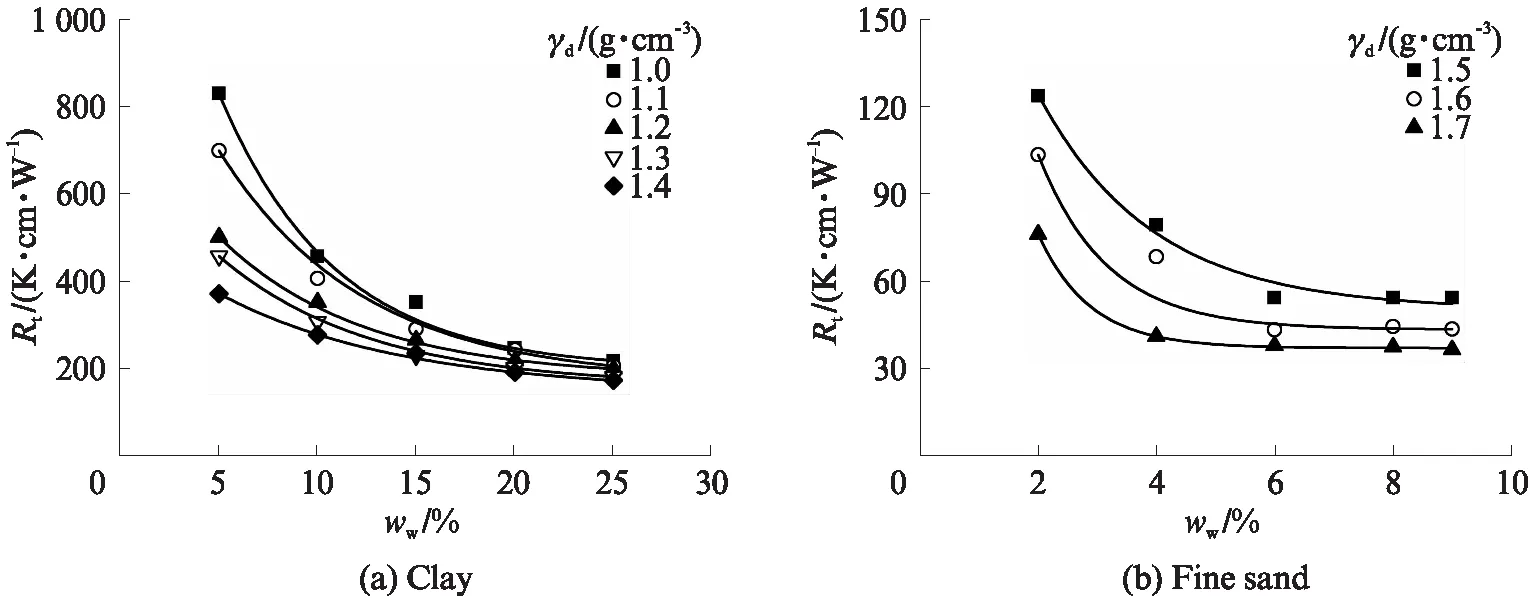
图1 含水量和干密度对土体热阻系数的影响Fig.1 Effect of moisture content and dry density on soil thermal resistivity[14]
2 ANN模型建立
2.1 人工神经网络
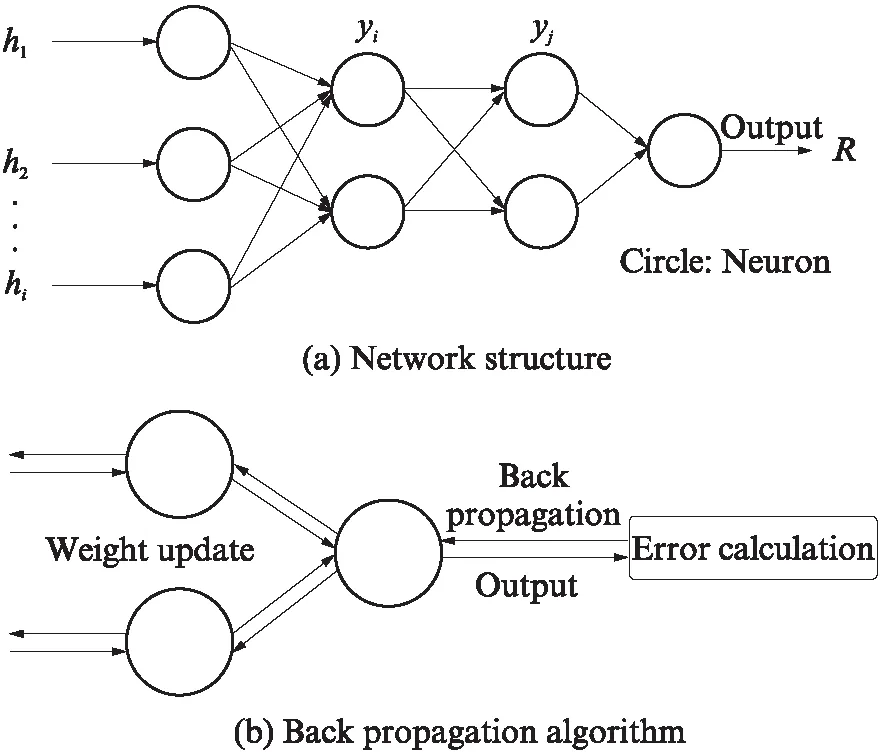
图2 人工神经网络结构示意图Fig.2 Sketch diagram of artificial neural network architecture
人工神经网络(ANN)一般由输入层、隐藏层和输出层3部分组成,每层之间通过赋有权重的神经元相互连接,每个神经元与下层所有神经元相连接. 图2(a) 为一个典型的多层前馈神经网络结构,其中h1、h2,…,hi为输入参数,yi和yj为隐藏层神经元,R为输出参数.反向传播算法是目前ANN较为流行的算法之一,通过将隐藏层内神经元的权重相乘并求和,再利用“激活函数”进行处理,根据实际输出值与目标值之间的误差来修改神经元的权重,从而达到不断“学习”的目的,最终得到满足误差要求的输出参数(如图2(b)所示).该算法在土木工程的基坑支护、隧道监测和边坡治理等领域得到了良好的应用[25-26].本文建立用于预测土体热阻系数的计算模型,在其训练阶段采用Levenberg-Marquardt反向传播算法.
图3为本文所提ANN预测模型计算流程示意图,其主要步骤为:(1)选择合理的模型输入参数;(2)划分数据库子集,用于交叉验证计算结果;(3)设置模型计算参数,包括传递函数f、误差限值、最大循环次数Cmax和动量因子μ等;(4)模型训练与验证;(5)优化计算模型结构,获得计算精度高、训练良好的最终模型.
2.2 模型数据库
如前所述,土体热阻系数受众多因素影响,其中含水量、干密度的影响显著且规律清晰,石英含量和颗粒粒径对于土颗粒和颗粒接触间的热传导性能具有决定性影响.此外,文中所有热阻系数值均为室温条件(20±2)℃下获得,细微的室温差别(≤2℃)对土体热阻系数的影响可忽略不计.针对上述问题,本文在ANN技术基础上,选用5种典型土体(黏土、粉土、粉砂、细砂和粗砂),以含水量(ww)和干密度(γd)作为输入参数,对其分别建立热阻系数单个计算模型.与此同时,以含水量(ww)、干密度(γd)、黏粒含量(c)和石英含量(qc)作为输入参数,建立所有类型土体的热阻系数广义计算模型.模型的输出参数均为热阻系数(Rt).5种类型土体的基本物理性质指标如表1所示.
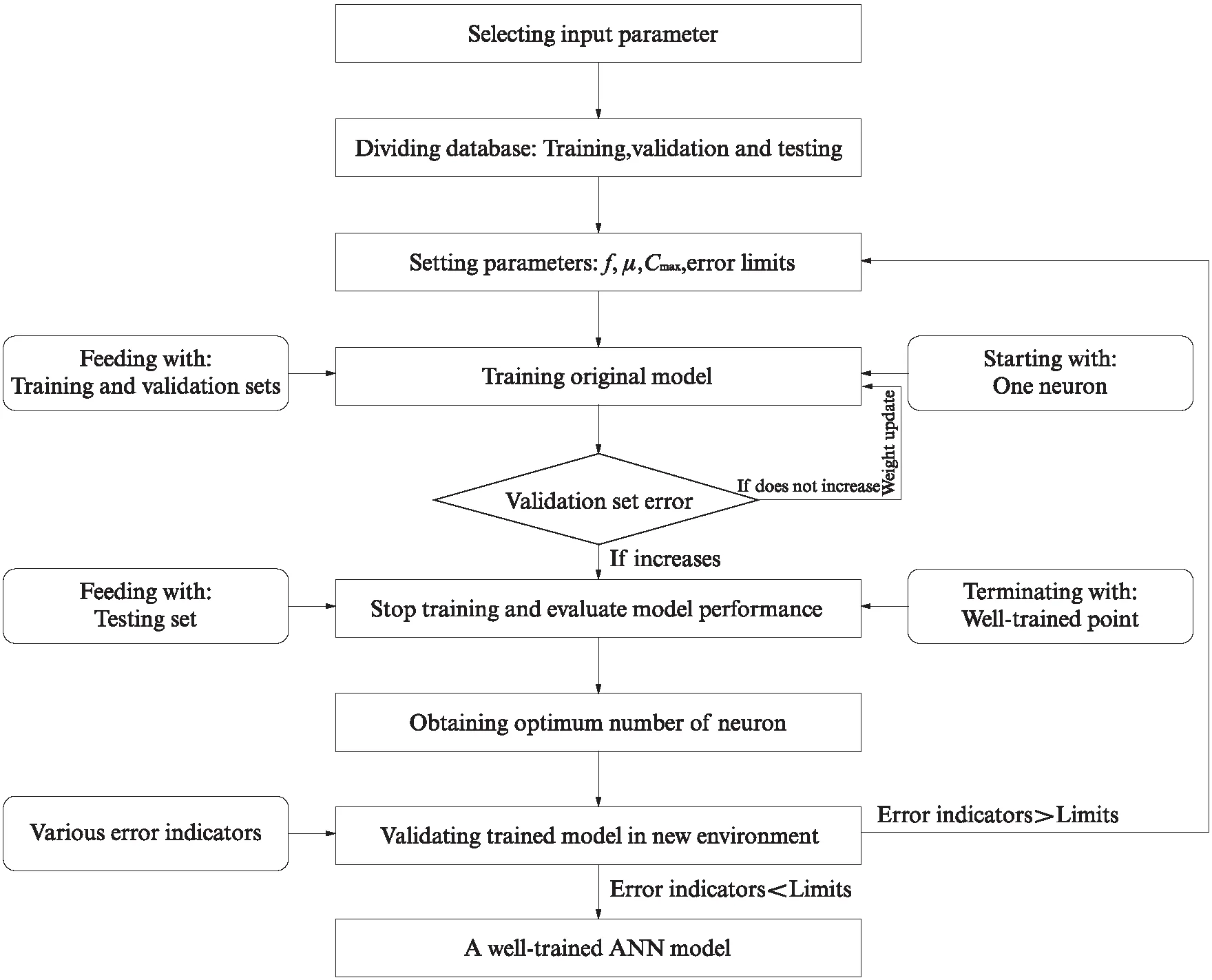
图3 ANN预测模型计算流程图Fig.3 Flow chart of proposed ANN prediction model
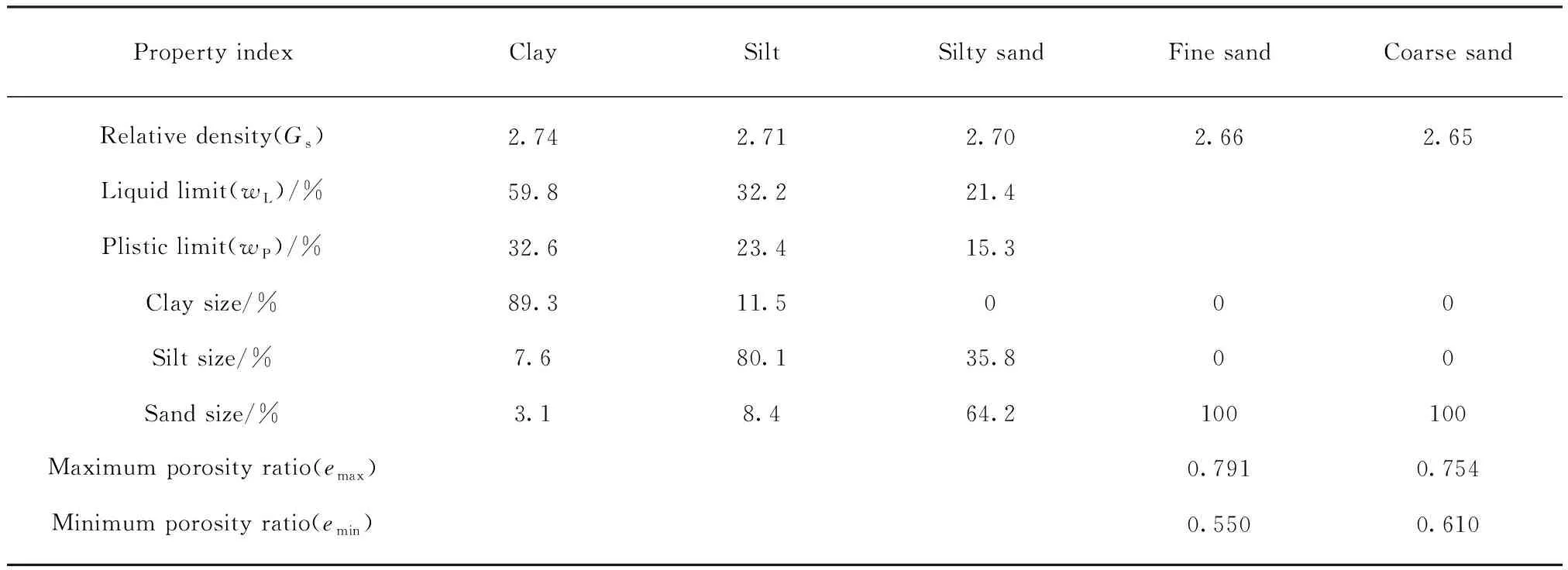
表1 土体基本物理性质指标
表2、3分别列出了单个计算模型和广义计算模型的输入参数、输出参数的边界值.表2中符号ANN-C、ANN-S、ANN-SS、ANN-FS、ANN-CS分别对应于黏土、粉土、粉砂、细砂和粗砂模型;表3中0%含水量的土样为干土,黏粒含量为0%的土样为砂性土;RtC为热阻系数的模型计算值.此外,对所有模型的输入、输出参数进行归一化处理,使其值在 0~ 1之间,归一化计算式为:
(1)
式中:xN为归一化值;x为实际值;xmin为实际最小值;xmax为实际最大值.待模型训练结束后,将各变量还原至初始的真实分布范围.
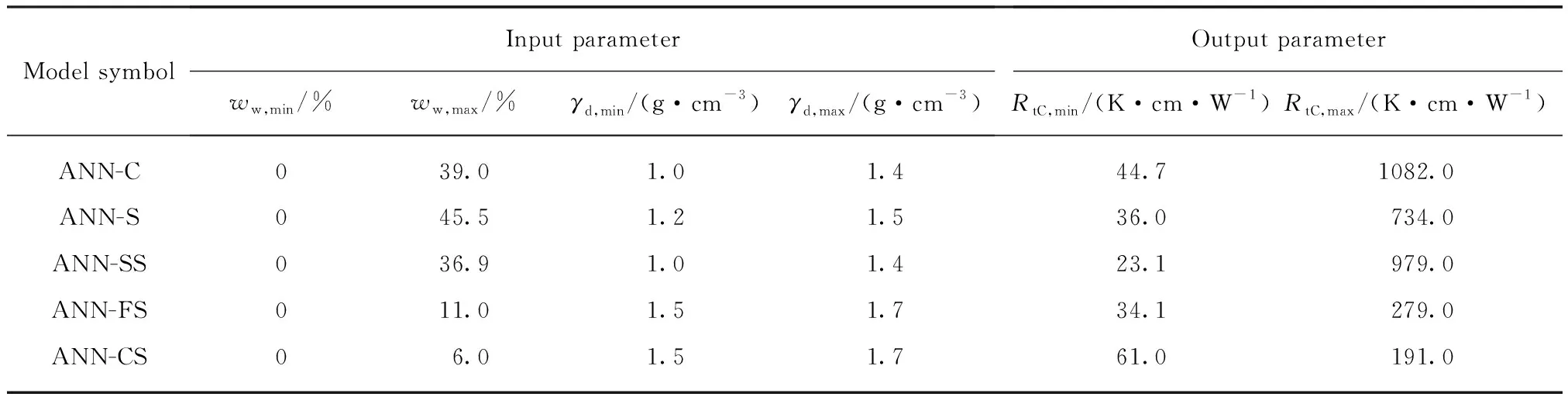
表2 单个计算模型输入参数和输出参数边界值
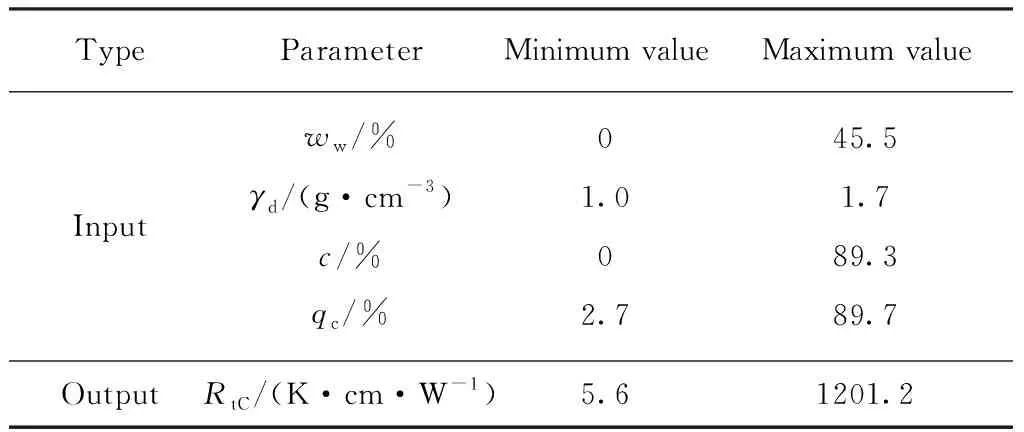
表3 广义计算模型输入参数和输出参数边界值
2.3 模型参数设置
人工神经网络技术通常将对象数据库划分为2个子集:(1)训练集,用于构建模型;(2)验证集,用于验证、评价模型的适用性能.然而这种划分方法可能会导致模型计算结果过度拟合,使得当前的训练模式不能更好地推广至新的数据环境.因此,根据已有相关研究报道,本文选用交叉验证作为终止标准的依据.在交叉验证中,数据库被划分为3个子集,即训练集、验证集和测试集.训练集用于更新训练网络的权重,在此更新过程中,时刻监测验证集的误差变化,当误差值开始增加时,立即停止训练,认为到达训练的最优点[27].然后,将测试集数据反馈至训练完成的网络中,用于评价该模型的性能优劣.本文训练集、验证集和测试集分别占整个数据库总量的55%、25%和20%.
土木工程设计通常选用具有1个隐藏层的神经网络,在连接权重充分的条件下,此类网络结构可以近似任何的连续函数.因此,本文模型的隐藏层数目设置为1个,隐藏层中神经元的数量从1开始逐次递增,每次增量为1,直至网络到达最优.设置2个动量因子μ1=0.010和μ2=0.001,用以寻求训练过程中神经网络的最佳结构和优化收敛速度.Erzin等[28]利用神经网络预测土体渗透系数,计算的样本容量、隐藏层数量以及最优结构的误差值选择标准均与本文模型存在一定的相似性;此外,土体热阻系数与渗透系数也具有许多相同的影响因素.因此,本文动量因子数值的选择参照文献[28]进行.最大训练次数设为1000次,选用相关系数R2和平均绝对误差MAE作为评价模型性能的指标.所有计算模型参数的设置如表4所示.已有研究证明,若隐藏层神经元数量和初始权函数选择得当,采用Sigmoid函数作为网络结构的传递函数,可以使网络以任意精度逼近1个多维映射.故本文表4中的传递函数均选用Sigmoid函数.网络结构经历多次训练优化,达到满足前述误差值要求的最优结构后,其单个计算模型和广义计算模型的输入参数权重值与偏差值计算结果如表5、6所示.
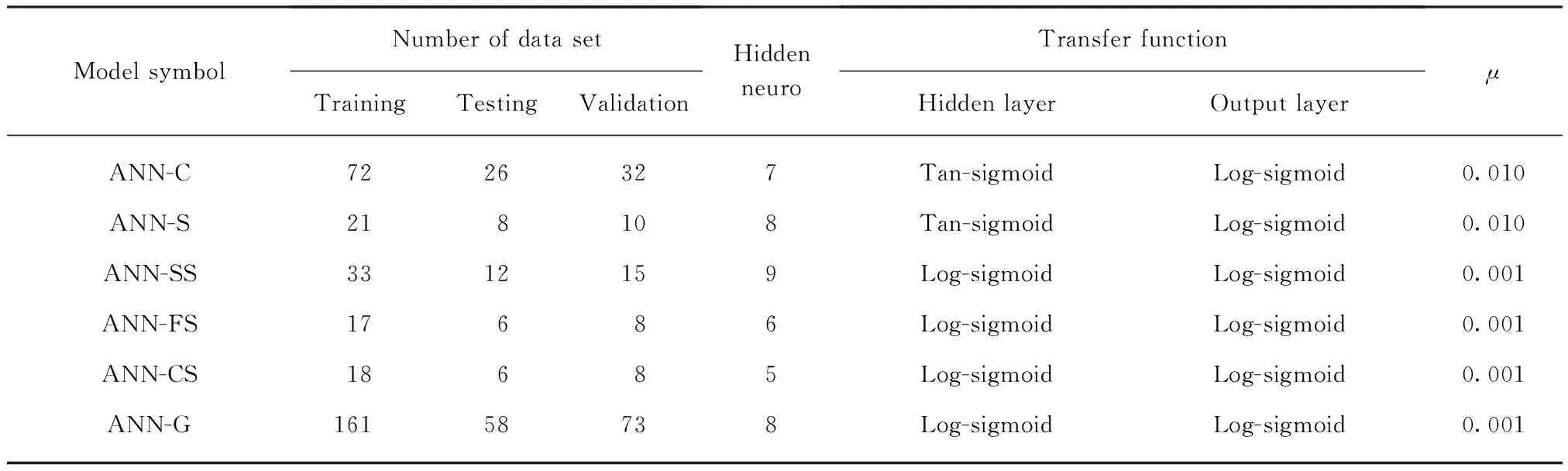
表4 计算模型关键参数设置
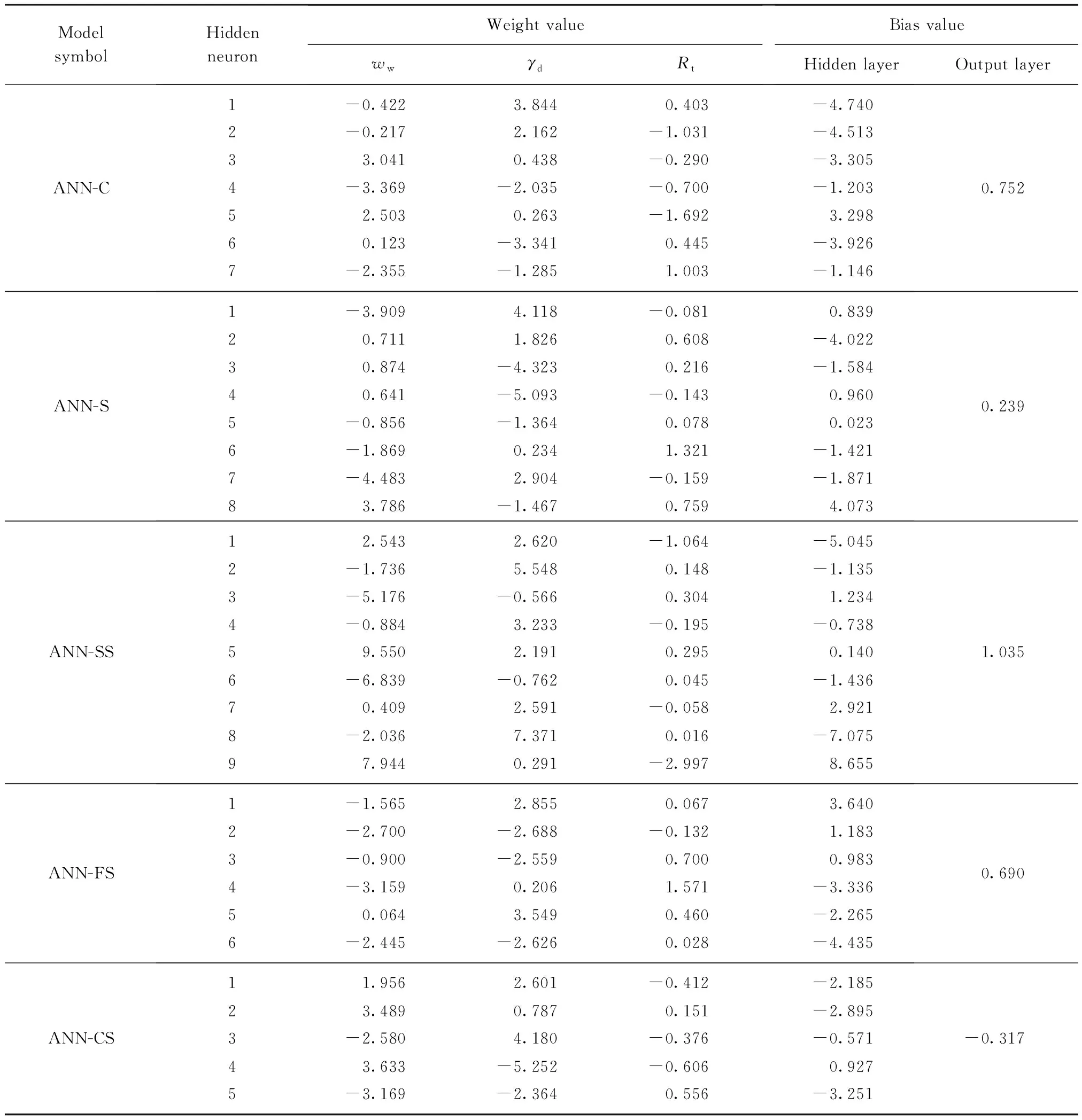
表5 单个计算模型输入参数权重与偏差值
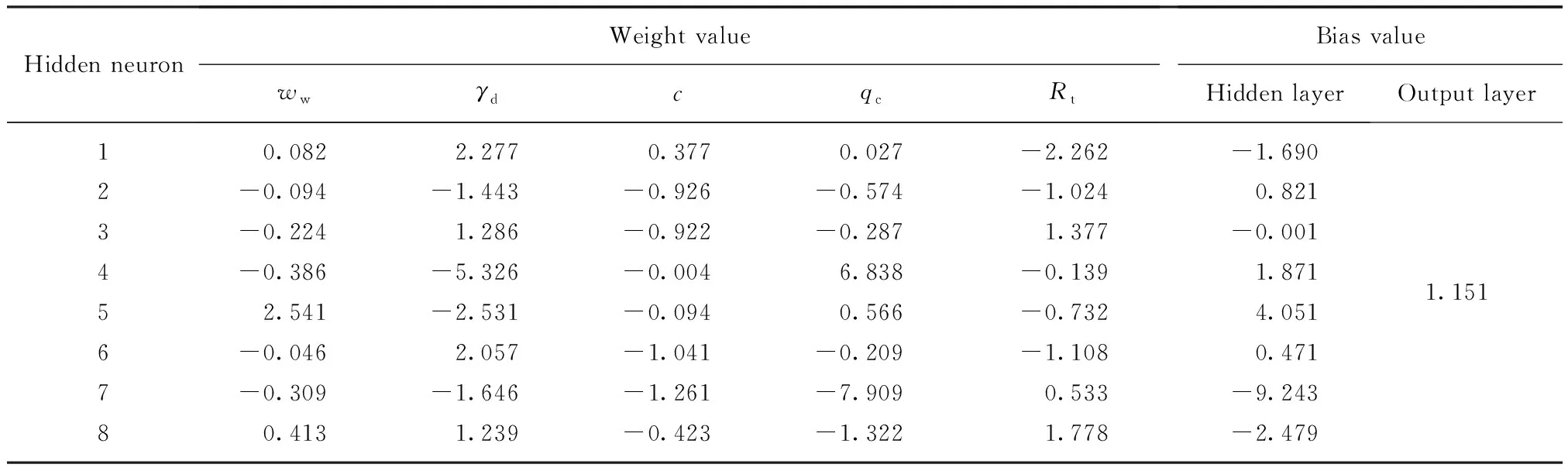
表6 广义计算模型输入参数权重与偏差值
3 模型验证
图4为不同类型土体热阻系数的单个模型计算结果RtC与实测结果RtM对比.由图4可见:(1)整体而言,热阻系数计算值与实测值较为吻合,模型计算结果表现出较高的精确度;(2)黏性土(黏土和粉土)计算结果的离散性较砂性土(粉砂、细砂和粗砂)高,这主要是细粒土颗粒的矿物成分多样、颗粒形态复杂等因素所致;(3)3个子集的训练结果保持一致,且均具有较强的预测能力.由此说明,ANN单个计算模型可以很好地预测特定类型土体的热阻系数,交叉验证方法亦有效、可行.
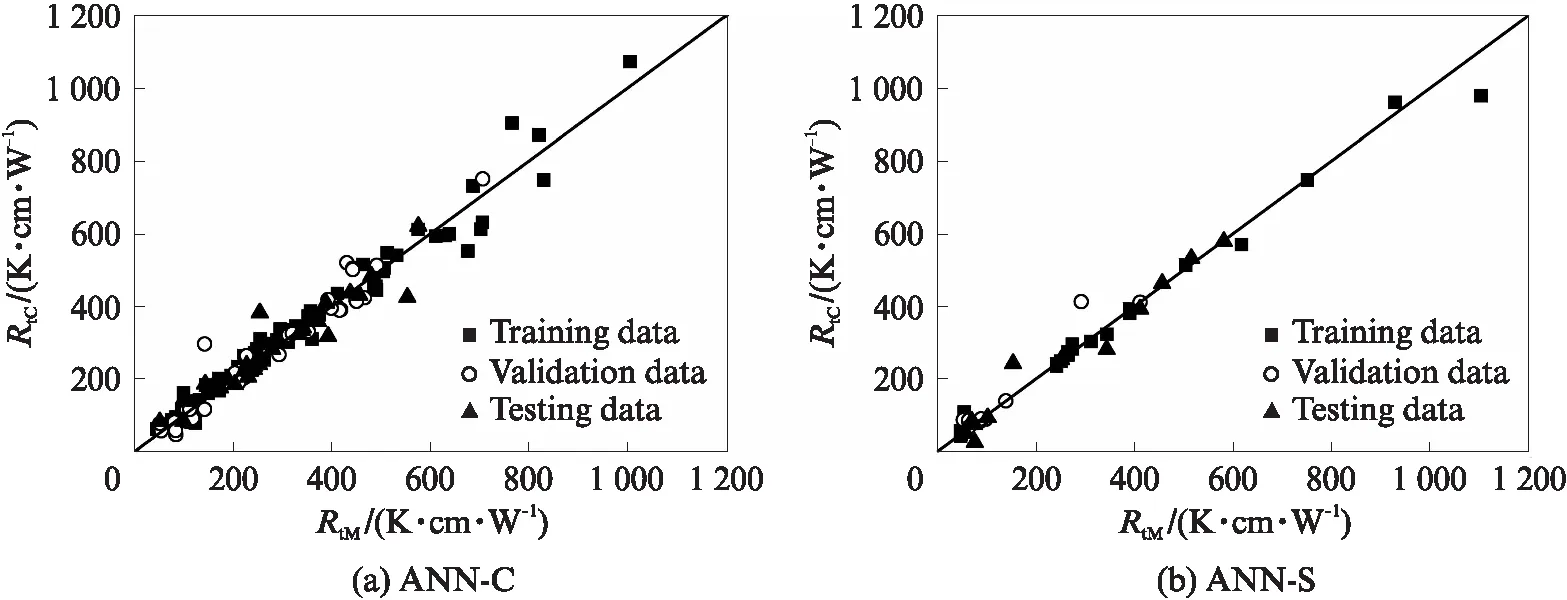
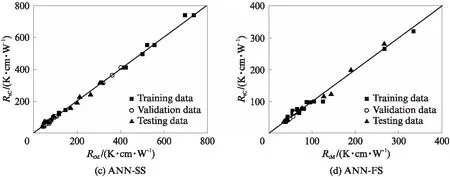
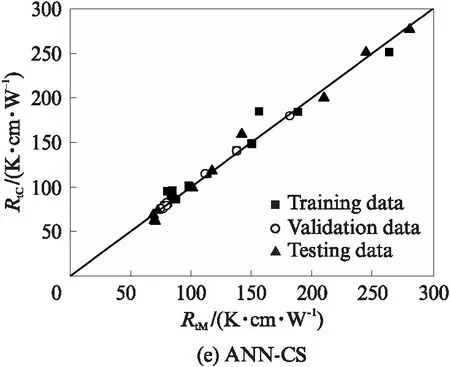
图4 单个模型计算结果验证Fig.4 Verification of calculation results for ANN individual models
为了增强ANN模型的适用性,本文对具有4个输入参数的广义模型(ANN-G模型)也进行了对比分析,其结果如图5所示.一般而言,在ANN结构相同的条件下,相关联的输入参数越多,训练后得到的计算结果越接近目标值.相比于单个模型,广义模型增加了黏粒含量c和石英含量qc这2个参数,两者分别对应颗粒粒径和矿物成分对土体热传导特性的影响.然而,样本容量和差异的增加又会降低模型预测结果的精度,2种效果之间会相互影响、抵消.图5中ANN-G模型对于5种类型土体热阻系数的预测表现出了良好的性能,RtC与RtM一致性较高.这表明,训练完成后的ANN-G模型对于不同土体热阻系数的预测是有效、可行的.
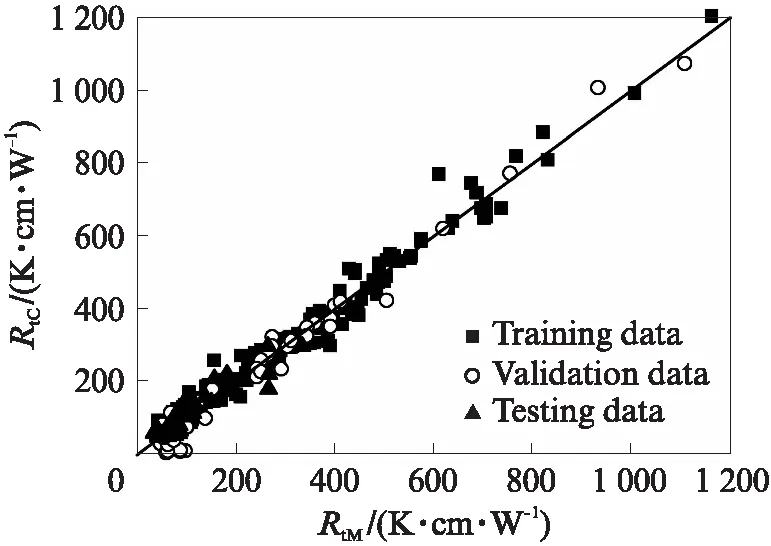
图5 广义模型计算结果验证Fig.5 Verification of calculation results for ANN generalized model
为了进一步定量评价ANN单个模型和广义模型的可靠性,除采用前述的相关系数R2和平均绝对误差MAE指标外,还选用了方差比VAF和均方根误差RMSE,2个误差指标的计算式分别为:
(2)
(3)
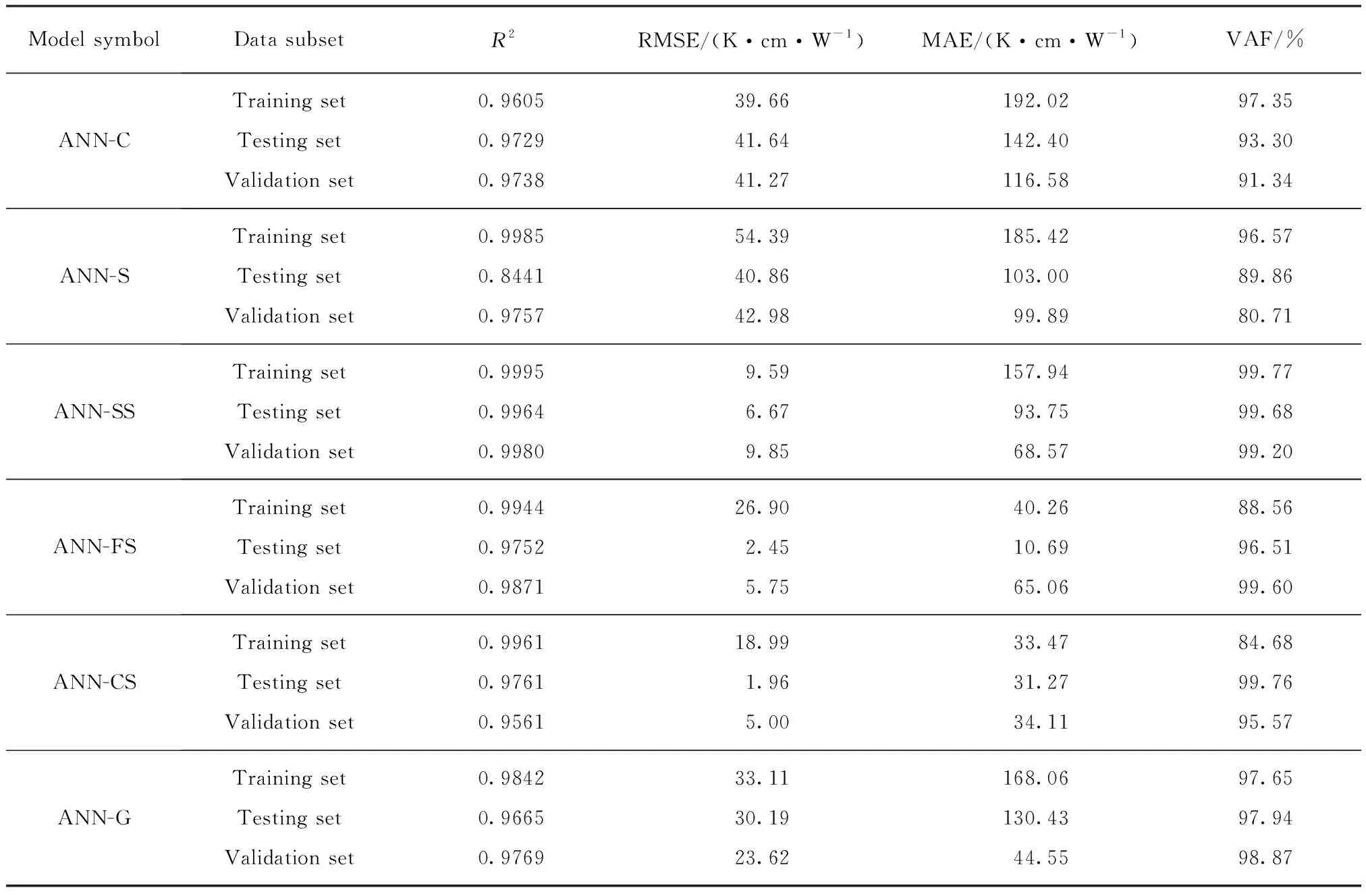
表7 ANN计算模型性能评价指标
4 模型性能评价
4.1 经验关系模型
目前,估算土体热阻系数的各模型中,理论模型计算过程复杂且参数要求较多,难以实际普遍应用;经验关系模型具有简单、易操作等特点,工程设计中大多采用此类方法.为了评价ANN模型预测土体热阻系数性能的优劣,本文选取了3个典型的经验关系模型,将其与ANN模型相对比.3个典型经验关系模型的背景和计算式概述如下:
(1)Kersten模型.Kersten[29]采用单根线柱热源径向加热的方式对19种类型土体的热阻系数/热导率进行了测试,并分析讨论了含水量、饱和度、矿物成分、温度和密度等因素对土体传热性能的影响,提出了估算不同类型土体热阻系数的经验关系式.
对于黏土或粉土:
Rt=[1.3×lgww+0.29]-1×10(3-0.01 γd)
(4)
对于砂性土:
Rt=[1.01×lgww+0.58]-1×10(3-0.01 γd)
(5)
式中:ww为含水量;γd为以lb/ft3计的干容重(1lb/ft3= 16.03kg/m3).
(2)Gangadhara模型.Gangadhara等[30]采用非稳态热探针技术对印度地区5种类型土体进行热阻系数测试,通过对试验结果的统计分析,提出如下经验模型:
Rt=[1.07×lgww+b]-1×10(3-0.01 γd)
(6)
式中:b是与土体类型相关的无量纲参数,对于黏土、粉土、粉砂、细砂和粗砂,其b值分别为-0.73、-0.54、0.12、0.70和0.73;ww为含水量.
(3)Cote模型.Cote等[31]对多种岩土材料(土、岩石和道路基层材料等)的热阻系数/热导率进行了测试,并在Johansen[20]提出的归一化模型基础上,建立了广义的归一化预测模型:
(7)
式中:ksat和kdry分别为饱和土和干土的热导率;kr为归一化热导率;Sr为饱和度;κ是反映土体类型对kr-Sr关系影响的系数.
4.2 模型计算对比
图6为黏性土热阻系数的各模型预测结果与实测值对比.由图6(a)可见:Kersten模型和Gangadhara模型的RtC值均具有明显“高估”的现象;Cote模型的RtC值与RtM值吻合较好,但仍存在部分数据点“低估”的现象;ANN单个模型的计算结果与实测值RtM吻合度最高,两者绝对误差控制在25%以内.由图6(b)可见,ANN-G模型的计算结果比3种经验关系模型更接近实测值,且相比于ANN单个模型的计算误差更低,其值在20% 以内.
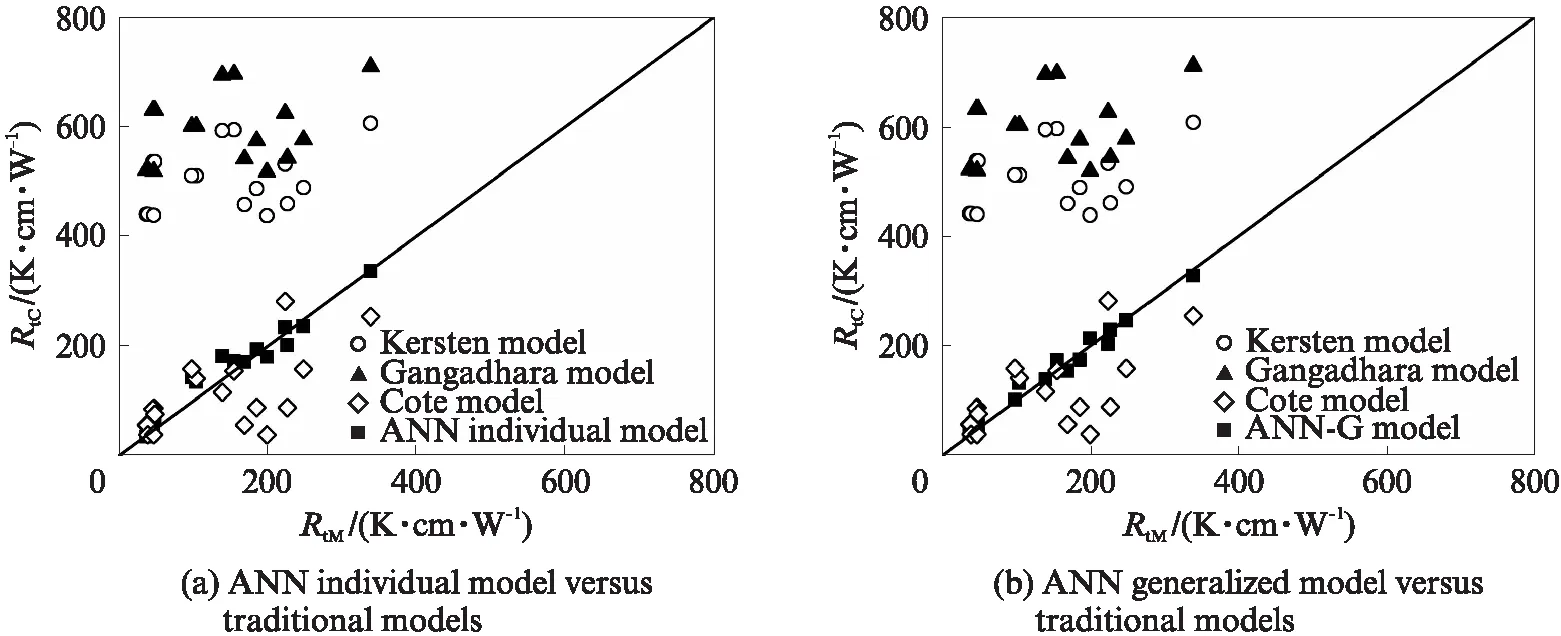
图6 黏性土热阻系数模型计算值与实测值对比Fig.6 Comparison between measured values and calculated values of clayey soils thermal resistivity with different models
图7为砂性土热阻系数的不同模型计算值与实测值对比结果.与图6中黏性土热阻系数计算结果相似,Kersten模型和Gangadhara模型的RtC值与RtM值之间存在较大误差,精确度较低.砂性土在Rt值较小状态下(Rt<200K·cm/W),Cote模型的预测结果精确度较高,但在Rt值较大状态下(Rt>200K·cm/W),该模型计算结果有明显“低估”现象.ANN单个模型和ANN广义模型对砂性土热阻系数的预测均表现出良好的性能,RtC值与RtM值之间的误差在15%以内.砂性土矿物成分和颗粒形态较黏性土单一,在一定程度上缩小了单个模型与广义模型预测结果之间的差距.
为了定量评价各个热阻系数预测模型的性能优劣,对上述预测结果的均方根误差RMSE值进行了计算,其结果如表8所示.由表8可见:不论是黏性土还是砂性土,ANN广义模型均表现出优于其他模型的预测性能(RMSE值最小);ANN单个模型的预测结果优于3个经验关系模型,其对于砂性土热阻系数的预测精度与广义模型相当,对于黏性土则稍逊;3种经验关系模型中,Cote模型的预测结果误差较小,其他2个模型的RMSE值较大,最大值约 467K·cm/W.整体而言,ANN广义模型的热阻系数预测结果最优,ANN单个模型次之,经验关系模型应用于新环境时均存在较大的预测误差.
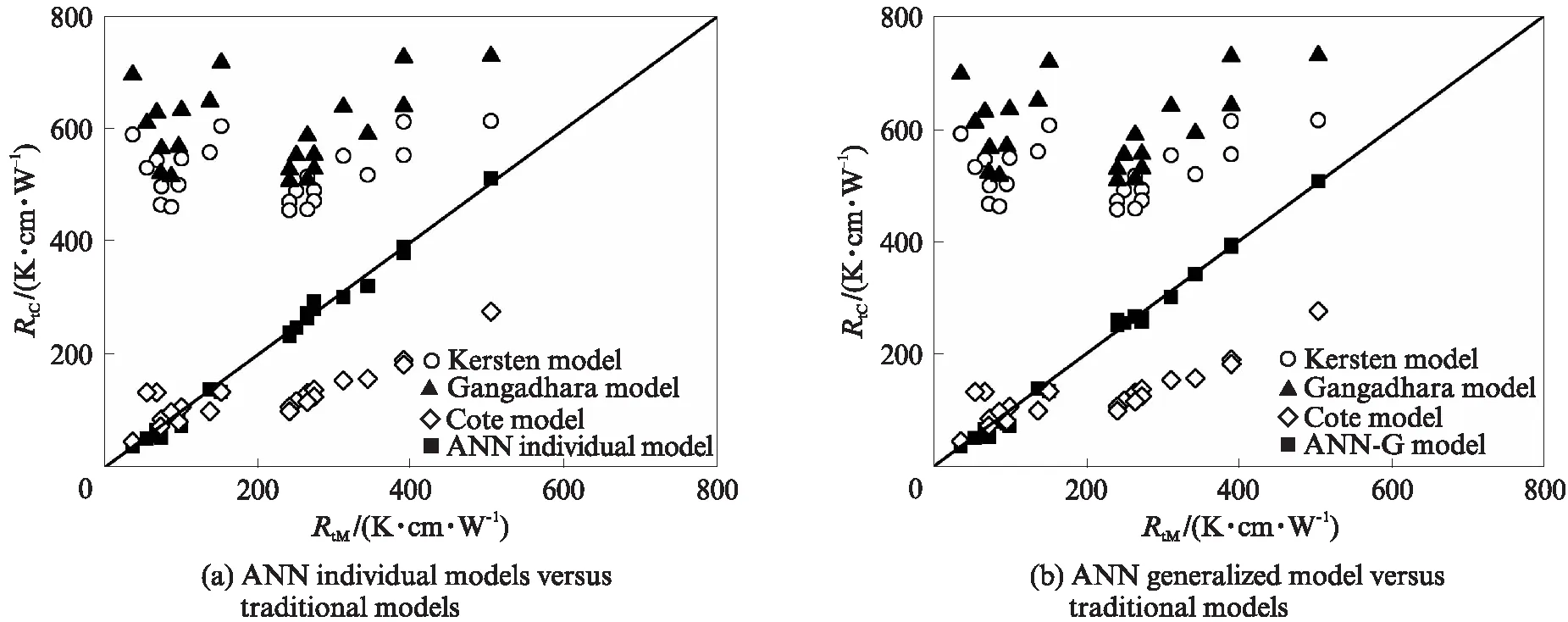
图7 砂性土热阻系数模型计算值与实测值对比Fig.7 Comparison between measured values and calculated values of sandy soils thermal resistivity with different models
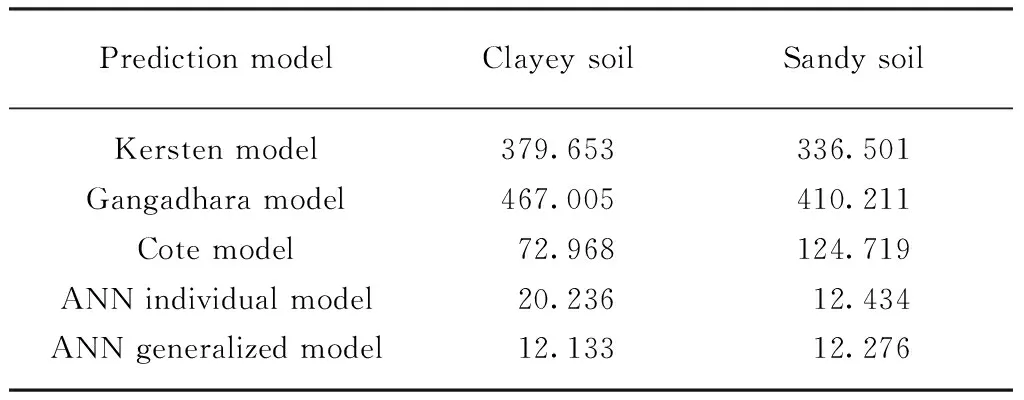
表8 各模型预测结果的RMSE值
对比上述计算结果可知,仅选用含水量、干密度和粗略表征土体类型的参数b作为计算参数,将难以准确估算土体热阻系数.这也从侧面验证了只有2个输入参数的ANN单个模型预测结果的精确度要低于ANN广义模型.Cote模型虽然考虑了较多因素对土体热传导性能的影响,计算结果优于其他2种经验关系模型,但仍存在一定离散性.对于工程性质参数有限、矿物成分不明的特定类型土体,可采用ANN单个模型估算其热阻系数;对于工程性质差异显著、沉积环境复杂的不同类型土体热阻系数预测,建议选用ANN广义模型更为合理.
5 结论
(1)基于人工神经网络的计算模型可以较好地预测土体热阻系数,以含水量、干密度为输入参数的ANN单个模型可用于预测特定类型土体的热阻系数;以含水量、干密度、黏粒含量和石英含量为输入参数的ANN广义模型可用于不同类型土体热阻系数的估算.
(2)交叉验证结果表明,ANN广义模型的精确度与ANN单个模型相当,增加相关输入参数可有效保证对多种类型土体计算结果的精确度.神经网络计算模型的精度显著优于传统经验关系模型,仅以含水量和干密度为计算依据的经验关系模型计算结果与实际值偏差显著,难以满足工程设计要求.新环境中ANN广义模型对于不同类型土体热阻系数的估算更胜于ANN单个模型.
(3)某一类型土体在物理化学性质尚不明确条件下,可采用ANN单个模型进行估算;对于工程性质差异明显、沉积环境复杂的不同类型土体,建议优先选用ANN广义模型来评价其传热性能.下一步可考虑针对孔隙液特征、颗粒形态和接触特性等因素影响,进行有关土体热阻系数更精细的计算模型研究.

