一种光伏组件无阴影遮挡时间计算方法
张 震
(中国能源建设集团江苏省电力设计院有限公司,江苏 南京 211102)
当前,全球可再生能源开发利用规模不断扩大,发展可再生能源已成为许多国家推进能源转型的核心内容和应对气候变化的重要途径,也是我国推进能源生产转型的重要措施。“十二五”期间,我国可再生能源发展迅速,为我国能源结构调整做出了重要贡献。而太阳能作为一种极具经济开发价值的清洁能源,近年来发展迅速。国家能源局最新数据显示,截止2018年底,全国光伏装机已达到1.74亿kW,占全部装机比例近10%。《太阳能发展“十三五”规划》提出“继续扩大太阳能利用规模,不断提高太阳能在能源结构中的比重,提升太阳能技术水平,降低太阳能利用成本”等发展目标。由此可见,光伏产业作为我国新能源产业发展的重要支撑点,具有极大的发展和增长空间。
在上述背景下,光伏产业蓬勃发展,各项技术趋近成熟,光伏电站整体造价呈现下降趋势。对光伏行业技术作更深入的剖析势在必行,而光伏组件无阴影遮挡的时间则是分析光伏电站经济性指标的一个重要参数[1]。目前,要记录光伏组件在一日中无阴影遮挡的时间,仅能通过对已运行的电站进行实际监测记录,但光伏电站所在山地坡度的差异,使日照时间记录极为困难。本文研究了一种新型的计算方法,可在项目设计初期光伏组件布置确定的前提下,根据光伏电站所在地纬度、电池组件长度、电池组件间距、电池组件倾角、山地坡度等参数计算光伏组件无阴影遮挡的时间。这一研究可在项目前期进一步优化光伏电站的组件布置,对电站的科学合理设计有着重要意义。
1 光伏组件无阴影遮挡模型分析
一般来说,决定光伏电站发电量的要素主要有三点,分别是光伏组件接收到的太阳辐射量,光伏组件无阴影遮挡时间,以及各电气设备的损耗。光伏组件接收到的太阳辐射量取决于项目地点太阳辐射量及光伏组件的安装倾角,电气设备的损耗则主要由设备本身所决定,故本文暂不讨论。对于光伏组件无阴影遮挡时间来说,在相同安装设计前提下,无阴影遮挡时间越长,光伏发电量越多,该内容是光伏电站建成后经济性评价的重要理论因素。本文试从光伏电站前期的设计过程中分析计算光伏组件无阴影遮挡时间的可行性。
1.1 光伏组件在水平面上的布置模型
以光伏电池阵列前后排均在同一水平面上为例,具体的布置示意图如图1所示。

图1 水平面上光伏电池阵列布置图
由图1可知:
D=Ycosβ
(1)
Y=H/tanα
(2)
式中:D为电池阵列相对间距;Y为太阳射线在地面上的影长;H为前排电池阵列最高点与地面垂直高度;α为太阳高度角;β为太阳方位角;L为电池阵列斜面长度。
由式(1)(2)可知:
D=Hcosβ/tanα
(3)
且根据相关研究[3],α、β与项目所在地的纬度、赤纬角和时角等参数具有如下关系[2]:
α=arcsin(sinφsinδ+cosφcosδcosω)
(4)
β=arcsin(cosδsinω/cosα)[3]
(5)
式中:φ为当地纬度;δ为赤纬角;ω为时角。
赤纬角,是阳光射线与赤道平面的夹角,太阳照射到北半球时为正,照射到南半球时为负,春、秋分时为0,一年之中,太阳赤纬角每一天都在变化,一年中从元旦之日起,第n天的太阳赤纬角计算为[3]:
(6)
时角,是由于地球的自转形成的,正午时时角为0,每小时的时角为360°/24=15°,上午时角为正,下午时角为负。

(7)
1.2 光伏组件在山地上的布置模型
在实际项目中,由于受到土地性质及地理环境等因素的影响,在同一水平面上布置光伏组件的情况较少,越来越多的光伏项目会选择在山地进行组件布置。
光伏组件布置在山体南坡或北坡时,光伏组件的布置示意图如图2或图3所示。

图2 山体南坡情况下光伏组件布置模型图
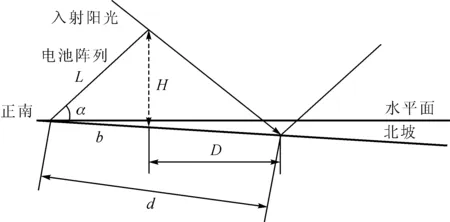
图3 山体北坡情况下光伏组件布置模型图
由图2、图3可知:
D=d×cosb-L×cos(a+b)
(8)
H=L×sin(a+b)-L×cos(a+b)×tanb-d×tanb
(9)
式中:d为光伏组件前后排间距;L为电池组件长度;a为光伏组件倾角;b为山地坡度(南坡为正,北坡为负,平坡为0);D为电池阵列相对间距;H为前排电池阵列最高点与地面垂直高度。
2 光伏组件无阴影遮挡时间的计算方法
2.1 理论无阴影遮挡时间分析
对于山地光伏项目来说,在确定项目地点后,项目所在地的纬度φ,项目所在地的山地坡度b,均为定值。在设计过程中,电池阵列斜面长度L,光伏组件倾角a,以及光伏组件前后排间距d均可以在设计初期进行设计规划。在已知上述条件的情况下即可求出1年当中某1天的无阴影遮挡的临界时角ω,从而分析出当天的无阴影遮挡时间Δt。
公式(3)等式两边同时平方可得:
(10)
由公式(4)可得:
cosα2=1-sinα2=1-(sinφsinδ+cosφcosδcosω)2
(11)
由公式(5)可得:
(12)
将公式(11)(12)代入公式(5),可得:
(13)
展开后并整理可得:
cos2ω(H2cos2δ-(H2+D2)cos2φcos2δ-
cosω(H2+D2)2sinφsinδcosφcosδ+
(H2sin2δ-(H2+D2)sin2φsin2δ=0
(14)
此时,令:
cosω=x
(15)
H2cos2δ-(H2+D2)cos2φcos2δ=A
(16)
(H2+D2)2sinφsinδcosφcosδ=B
(17)
H2sin2δ-(H2+D2)sin2φsin2δ=C
(18)
不难发现,此时等式已经变成了一元二次方程,即:
(19)
ω=arccosx
(20)
结合公式(7),可得当天的理论无阴影遮挡时间Δt:
t1=-ω/15+12
(21)
t2=ω/15+12
(22)
Δt=t2-t1
(23)
式中:t1为上午光伏组件无阴影遮挡临界时间;t2为下午光伏组件无阴影遮挡临界时间;Δt为理论无阴影遮挡时间。
2.2 实际日照时间分析
早上太阳升起到下午太阳落山的这段时间,实际日照小时数ΔT计算为[4]:
(24)
2.3 光伏组件实际无阴影遮挡的时间
通过比较理论无阴影遮挡时间及实际日照时间ΔT。较小值即为光伏组件实际无阴影遮挡的时间。
3 验证过程
以江苏某一项目地为例,通过现场踏勘测得,该厂址纬度为φ=31.61°,场地坡度倾角b=0°。并且根据可行性研究设计,光伏组件采取双排布置,即L=3.32 m,光伏组件倾角α=26°,组件前后排间距d=7.2 m。
运用本计算方法进行计算冬至日(12月21日)光伏组件无阴影遮挡的时间。
冬至日为1年当中的第355天,所以:
(25)
可以求得,前排电池阵列最高点与地面垂直高度H,电池阵列相对间距D:
D=d×cosb-L×cos(a+b)=4.216 0 m
(26)
H=L×sin(a+b)-L×cos(a+b)×tanb-d×tanb
=1.455 4 m
(27)
此时,可以计算光伏组件无阴影遮挡时的临界时角ω:
(28)
那么,理论无阴影遮挡时间Δt:
Δt=ω/15+12-(-ω/15+12)=7.741 8 h
(29)
而太阳一天当中照射时间ΔT:
(30)
因为Δt<ΔT,即Δt为光伏组件实际无阴影遮挡的时间。
所以,若在工程地点,采用可行性研究中方案进行组件布置,则在冬至日光伏组件实际无阴影遮挡的时间为7.741 8 h。
而根据光伏电站建成后实际测量数据发现,冬至日光伏组件无阴影遮挡时间为7 h 45 min,即7.75 h,计算结果与实际测量数据一致。所以本计算方法是可行的。
4 结 语
目前在光伏电站前期设计中,光伏组件无阴影遮挡时间很难被计算,本文基于这一难题,在已知光伏电站所在地纬度、电池组件长度、电池组件间距、电池组件倾角、山地坡度等关键参数后,探索了一种光伏组件无阴影遮挡的时间的可行性计算方法,但是该方法为全天天气晴朗条件下的计算结果,实际运用时还应该结合多年天气变化情况来计算。该方法为光伏电站的全面分析提供了重要途径,可在项目前期有效优化项目各项参数指标。

