海洋起重机冲击载荷研究

郭宏亮 隋振华，2

1 上海振华重工(集团)股份有限公司2 中交公路长大桥建设国家工程研究中心有限公司

1 引言

随着起重机的大型化、高速化和轻量化发展，其动力学研究显得愈发重要。起重机的冲击载荷问题是指钩头部分突然加载或卸载引起的臂架头部载荷显著变化，如起吊物从静止到稳态上升过程中速度增加，导致钢丝绳拉力增大。这会导致起重臂的弹性势能做功，引起应力的增加，甚至发生倾覆。

研究冲击载荷，探究其形成的理论原因，将对工程设计具有积极的意义。本文从力学原理上研究冲击导致载荷增大的原因及相应的计算方法，并通过有限元计算对推理过程进行验证。

2 起升载荷冲击现象及理论分析

如图1所示，起重机的起吊模型可以简化为一个质量为M的重物及垂直牵引它刚度为K的钢丝绳。

图1 起吊模型

冲击问题因速度变化而产生。当速度为0时，钢丝绳被稳定拉伸，其拉力等于重力Mg。当速度由0突然变为V时，根据振动理论，可以得出动力学方程：

(1)

求解该方程，即可得圆频率:

(2)

故重物自由振动的振幅为:

(3)

因此，在振动过程中，钢丝绳的最大拉力为自由振动达到最大振幅(即钢丝绳具有最大拉伸量)时的拉力：

(4)

为方便应用，可用冲击系数φ来描述这一现象。

(5)

从式(5)可以看出，影响冲击载荷(冲击系数)的主要原因包括稳态起升速度V，悬吊系统刚度K及悬吊物质量M。起升速度V主要来源于电机和卷筒，海浪导致的船体运动(垂荡和纵摇)等，其为冲击载荷的外因。悬吊系统的刚度K则取决于起重机的固有结构，是内因。

3 起重机的刚度计算

从整体概念说，悬吊系统包括牵连重物的钢丝绳及起重机的钢结构，因此起重机的刚度可以分解为以下4个部分(见图2)：

(1)起升系统K1，主要指直接连接吊重的钢丝绳。

(2)俯仰绳+臂架系统K2，这一部分的刚度主要指俯仰绳的伸长和臂架的变形。

(3)人字架或桅杆系统K3。

(4)筒体部分K4。

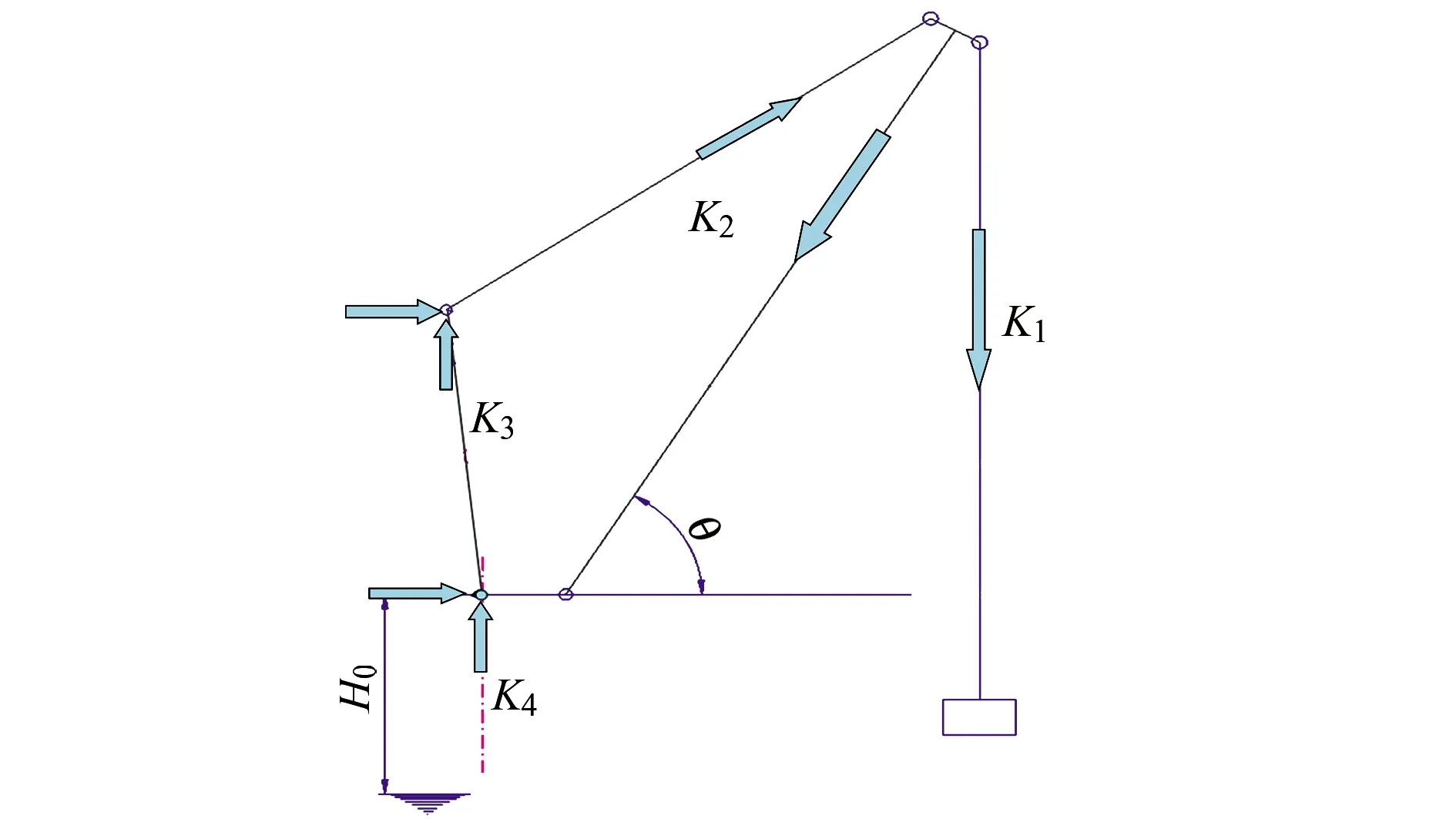
图2 起重机刚度分解

3.1 起升系统

起升系统主要是指起吊载荷的钢丝绳。起升系统通常由2个连贯的部分组成，一个是卷筒端到臂架头部的单根部分，另一个是臂架头部吊钩定动滑轮之间的多倍率部分。当吊钩处滑轮缠绕倍率较小时，卷筒端到定滑轮部分的变形对整体影响比较大，这常见于较小的吊钩。

如图3所示，单根钢丝绳从卷筒端R0，绕经滑轮R1，R2，R3，到达臂架头部定滑轮组R4，然后通过滑轮组增大倍率到达吊钩端的R5。

考虑单根钢丝绳截面积为A，弹性模量E，从R0端到R4端的总长度为L04，从R4到R5端高度为L45，吊钩端的倍率为n，吊钩处作用的垂直载荷为F。则L04的伸长量为：

图3 起重机起升系统

(6)

L45的伸长量为：

(7)

L04导致的钩头向下位移量将被滑轮组倍率稀释为Δ04/n，所以，起升系统部分导致的钩头向下位移量为：

(8)

起升系统的刚度为：

(9)

3.2 俯仰绳+臂架系统

在空间上，俯仰绳(L12)和臂架(L02)构成了一个三角形，维系着臂架铅垂平面的稳定(见图4)。俯仰绳受拉，端点下移，臂架受压，端点后移。

图4 俯仰绳+臂架系统

可以用解析这个三角形的办法获得相应刚度，臂架头部的变形计算如下。

根据轴向力变形公式计算变幅绳的伸长量：

(10)

根据轴向力变形公式计算臂架的轴向压缩量：

(11)

由上，可计算出钩头受力变形后的变幅绳长度L′12=L12+Δ12，臂架长度L′02=L02-Δ02。根据P0、P1坐标和新的变幅长度L′12和臂架长度L′02，计算臂架头部P2的新坐标(X′2，Y′2)。变幅和臂架系统在外力F作用下，引起的臂架头部下移量为Δ2=Y′2-Y2。其中Y2是变形前臂架头部的纵坐标。可得俯仰绳+臂架系统刚度为：

(12)

3.3 人字架或桅杆系统

人字架或桅杆用来撑起俯仰绳的上端点，在比较大型的起重机，一般采用人字架(A架)的形式，因为是三角布局，整体刚度比较好。在近海起重机中，为了节约空间，经常做成桅杆形式，桅杆上细下宽，桅杆整体成悬臂梁形式，在俯仰绳拉力作用下，顶端更容易变形。

当变幅绳水平分力比较大时，人字架或桅杆顶端向前位移，从而导致变幅臂架三角形整体向前向下倾转，使臂架头部产生向下位移Δ3。可得人字架或桅杆系统刚度为：

(13)

3.4 圆筒体部分

圆筒体坐落于人字架之下，在近年发展的风电安装平台中，筒体经常是高度方向的尺寸远大于直径，这使得筒体作为一个悬臂梁，其末端弯曲变形不可忽略。

圆筒体部分的受力特征以垂直方向的压力和向前的倾覆为主要特征，可通过计算压弯变形获得筒体顶端的垂直变形量以及倾覆平面内的角变形量。根据角变形及起重机整体尺寸，继而可以求得其引起的臂架头部的垂直变形量Δ4，可得圆筒体部分刚度为：

(14)

3.5 起重机的整体刚度

各分项刚度K1，K2，K3和K4成串联关系，统合起来，起重机的整体刚度为：

(15)

4 起重机整体刚度计算的有限元验证

用有限元方法也可以获得起重机的刚度。建立包含圆筒体在内的起重机模型，在臂架头部施加垂直向下一个单位的载荷，静态计算该载荷引起的位移Δ234，则1/Δ234即为起重机钢结构贡献的刚度。

前述过程从理论上推导了起重机刚度的组成部分，为了验证其准确性，对某600 t起重机不同臂架仰角下的刚度用前述理论和有限元模型分别进行计算，计算结果比较见图5。

图5 起重机刚度有限元计算和理论计算比较

由图5可见，理论计算结果和有限元计算结果吻合度非常高，证明上述推导的理论计算是可行的。理论计算公式可以编制为EXCEL程序，通过简单的几个输入参数，就可以迅速获得起重机的整体刚度值。这可省去繁琐的有限元建模过程，提高工作效率。

5 结语

随着起重机向高速化、大型化、轻量化发展，起重机的载荷冲击问题受到更多的重视。从理论上着手，分析了冲击载荷背后的结构动力学原理，分解了起重机的刚度组成，相应地提出了刚度计算的公式方法，经有限元分析证明计算方法的正确性，为起重机的刚度计算提供了更加快捷的途径。