对马克思价值转形问题中鲍特凯维兹传统的批判

张晓倩 王明扬

(中共中央党校，北京 100091)

价值向生产价格的转化被西方学者称为转形问题，并把它视作劳动价值论的核心。转形问题也是马克思主义经济学者内部以及与西方主流经济学者之间争论最激烈的主题之一。鲍特凯维兹最先将简单再生产平衡条件和一般利润率条件结合起来，尝试解决转形问题。之后的学者或者以鲍特凯维兹传统为基础，对其解决方法进行完善和发展；或者完全抛弃鲍特凯维兹传统，提出新的转形问题研究视角。本文旨在构建基于鲍特凯维兹传统的价值转形模型，运用归谬法对鲍特凯维兹传统进行批判。

一、马克思关于一般利润率规律的论述

马克思在《资本论》第三卷第九章以五个资本有机构成各不相同的生产部门为例，抽象地考察了一般利润率的形成和价值转化为生产价格的过程。一般利润率规律所描述的就是价值向生产价格的转化问题。他使总利润等于总剩余价值，总价格等于总价值，用总剩余价值与总预付资本相比得出一般利润率，每个资本家都依照一般利润率获得平均利润，成本价格加上平均利润就是生产价格。但马克思并没有说明不变资本和可变资本(生产要素)的生产价格化过程。他虽然提到了这一点，但只是说“一个商品的生产价格，对它的买者来说，就是它的成本价格，……必须记住成本价格这个修正了的意义，”[1]却没有详细论述。

紧接着在第十章中马克思试图说明一般利润率通过竞争而平均化的实际过程。他明确指出“这种平均化显然是结果，而不可能是起点，”[2]并在整章中始终把一般利润率作为结果并试图说明它的实现过程。马克思论述资本通过竞争实现一般利润率时思路很明确，第一步论述部门内竞争使不同厂商生产的同一种商品形成统一的市场价值，第二步论述供求偏离使价格和价值相偏离，第三步资本流动导致供求偏离使得商品价格偏离其市场价值，各部门利润率相等时的价格就是生产价格。可见生产价格只是价格的一种特殊形式，说明了价格的形成也就说明了生产价格的形成。问题的关键是资本流动如何导致供求偏离进而导致价格偏离的。这一点马克思并没有告诉我们。

总体看来，转形问题存在三个争议：一是生产要素的生产价格化问题；二是“两个相等”①是否成立的问题；三是一般利润率形成的具体过程。这三个问题交织在一起，只有在不同资本相互联系的错综复杂的总体运动中才能研究清楚。而且，如果出现生产过剩就不可能实现平均利润，在不考虑再生产平衡条件的情况下研究一般利润率的形成是没有意义的。因此，马克思在第九章中的数学计算可以当作示例来对待，②解决价值转化为生产价格的问题必须与社会总资本再生产理论相结合。

二、转形问题中的鲍特凯维兹研究传统

鲍特凯维兹(Bortkiewicz，1906，1907)最先尝试解决转形问题。③他对马克思的代数解决方法进行了修正，划分了三个部类(生产资料部类、工人消费品部类、奢侈品部类)，把简单再生产平衡条件和平均利润率条件结合起来构建了如下方程组：

c1x+v1y+r(c1x+v1y)=(c1+c2+c3)x

c2x+v2y+r(c2x+v2y)=(v1+v2+v3)y

c3x+v3y+r(c3x+v3y)=(s1+s2+s3)z

其中，x、y、z分别为三个部类的价格转换系数，r为平均利润率。

在这三个方程式中有四个未知数x、y、z、r，无法求出单一解，因此应增加一个方程式或减少一个未知数。鲍特凯维兹令总价值等于总价格构建了第四个方程式，但在实际计算中没有利用这个条件，而是假设奢侈品部类的价格系数z=1，由此减少一个未知数，z④完成求解。鲍特凯维兹据此得出结论，总利润始终等于总剩余价值，只有当奢侈品部类的资本有机构成等于社会平均资本有机构成时，总生产价格才等于总价值。

鲍特凯维兹的方法表明一个价格计算体系是可以从一个价值计算体系中推演出来的，因此，之后的学者在鲍特凯维兹三个基本方程式的基础上，或者利用总价值等于总价格这一条件构建第四个方程式(温特尼茨，1948)，⑤或者假设第二部类资本有机构成等于社会平均资本有机构成即令y=1(米克，1956)，⑥或者同鲍特凯维兹一样，假设第三部类资本有机构成等于社会平均资本有机构成即令z=1来说明“两个相等”的成立(塞顿，1957)。⑦他们都遇到了“两个相等”无法同时成立的问题，即使成立条件也非常苛刻。

Diaz和Velasco(2016)利用马克思的扩大再生产图式和“两个相等”条件构建了动态模型。⑧他们由“两个相等”条件求出平均利润率，进而求出价格系数ati。在举数值例进行说明时，由于at1>1，即高于价值出售，因此会有一部分资本被“束缚”，而第二部类会有部分资本“游离”出来。Diaz等令两部分资本相等，根据at1的值又求出一个at2，与之前所求的at2不相等。但是他们并未说明为什么会求出两个不等的数值，而是在数值例中直接用了第二个at2的取值。他们的数值例显示到第15年价格不再变化，系统达到稳定状态。另外，他们指出，要想在“两个相等”条件的基础上解决转形问题，必须放弃基于固定(名义或实际)工资率的限制性假设。实际上，Diaz和Velasco仍然是基于鲍特凯维兹传统解决转形问题，只是他们通过加入“两个相等”条件、考虑资本的“游离”和“束缚”、放弃固定工资率假设等，求出了一般解。但固定工资率实际上是劳动力再生产他自身所需要的生活资料的价值，放弃这一假设意味着工资可能远远低于劳动力价值，这是不现实的，也不符合马克思的工资理论。

国内基于鲍特凯维兹传统研究转形问题的学者，主要以沈民鸣(2008，2016)为代表，他在鲍特凯维兹的模型基础上提出了从两部类、三部类至n部类的转形模型，并论述了“两个相等”同时成立的情况。⑨但他认为价值转形不是通过生产资料和劳动力的流动实现的，而是通过社会对资本有机构成不同的部类所耗费的劳动给予不同程度的承认实现的，因为资本流动会破坏原有的再生产平衡。此外，沈民鸣把转形问题分为理论上的价值转形和价值转形的历史过程两种类型，他认为实际的价值转形过程是动态的、非均衡的，无法用数学方法准确描述，因此只讨论理论上的价值转形。

总的来看，基于鲍特凯维兹传统研究转形问题的学者都利用了再生产平衡条件，也就是将转形问题与社会再生产结合起来，这是值得肯定的。他们都将研究重点放在了“两个相等”同时成立的论证上，但其成立条件要么非常苛刻，要么不符合马克思关于价值转化为生产价格的论述。

三、基于鲍特凯维兹传统的价值转形模型

鲍特凯维兹及其后的学者已经证明，仅利用再生产平衡关系构建的方程组缺少条件。解决办法是或者引入“两个相等”条件，或者令某一部类的价格系数等于1。首先，令某种商品的价格系数等于1是不合理的。因为，即使是货币商品也仍然要以生产价格和其他商品交换，这一点和一般均衡分析有本质区别。其次，根据马克思关于一般利润率规律的论述，“两个相等”条件是一个整体，我们没有任何理由令模型只满足其中一个条件而舍弃另一个条件。因此，如果只是总量分析，为了补足条件只能令“两个相等”同时成立。

不管是鲍特凯维兹等人基于简单再生产的静态模型还是Diaz和Velasco基于扩大再生产的动态模型，结论都是价值体系可以转化为稳定的价格体系。因此，我们只需要用均衡分析的方法考察这个稳定状态是否存在即可。

(一)简单再生产条件下的转形模型

我们首先研究简单再生产过程，假设社会再生产已经实现了平均利润率并保持稳定，因为是简单再生产，每一期的总商品价值都相等。任一期期末总商品产品的价值形式可以表示如下：

Ⅰ：c1+v1+m1=W1

Ⅱ：c2+v2+m2=W2

其中资本有机构成ki和剩余价值率m'i保持不变并满足关系：ci=kivi，mi=m'ivi。价值价格转化系数ai=Pi/wi(Pi为产品价格，wi为产品价值)。i=1，2。则总商品产品的价格形式可以表示为：

a1c1+a2v1+p1=a1W1

(1)

a1c2+a2v2+p2=a2W2

(2)

两部类按价值计算的利润率不相等，经过竞争形成了一般利润率r，两部类资本家都获得了平均利润：

p1=(a1c1+a2v1)r

(3)

p2=(a1c2+a2v2)r

(4)

简单再生产的实现条件为：c2=v1+m1，用价格形式可表示为：

a2v1+p1=a1c2

(5)

马克思认为通过竞争，高资本构成部门产品的生产价格高于其价值，低资本构成部门产品的生产价格低于其价值，两者差额正好相抵，总利润等于总剩余价值，总生产价格等于其价值总和。用方程式表示如下：

a1W1+a2W2=W1+W2

(6)

p1+p2=m1+m2

(7)

(1)-(7)式联立方程组，已知k1、k2、m'1、m'2，求解a1，a2，v1，v2，P1，P2，r。

方程组求解：

由(3) (4) (7)得

(8)

由(5)得

p1=a1c2-a2v1

(9)

将(9)代入(1)得

a1(v1+m1-c2)=0

(10)

因为a1≠0，若a1有解，则v1+m1-c2=0，即v1+m1=c2。

由(7)得

p2=m1+m2-p1

(11)

将(9)(11)代入(2)得

(12)

若(10)成立，则将c2=v1+m1代入(12)得a2=1

将a2=1代入(6)得a1=1

由(1) (2)得p1=m1，p2=m2

显然，如果存在我们所假设的稳定状态，则必须满足两部类按价值计算的利润率相等，此时根本不存在价值向生产价格转化的问题。而我们是在假设两部类按价值计算的利润率不相等的情况下，考察通过资本竞争已经实现了平均利润率的状态能否保持稳定，这显然是矛盾的，说明我们假定的稳定状态无法实现。

(二)扩大再生产条件下的转形模型

我们再来研究扩大再生产的情况。相比简单再生产，需要再增加两个变量，设第一部类积累率为e1，第二部类积累率为e2。另外，因为扩大再生产不是简单的重复，所以还需要区分不同的时期。我们任取一期t，t期末总商品产品的价值形式可以表示如下：

Ⅰ：ct1+vt1+mt1=Wt1

Ⅱ：ct2+vt2+mt2=Wt2

其中资本有机构成ki和剩余价值率m'i保持不变并满足关系：ci=kivi，mi=m'ivi。设积累率为ei，价值价格转化系数ai=Pi/wi(Pi为产品价格，wi为产品价值)。i=1，2。则t期末总商品产品的价格形式可以表示为：

a1ct1+a2vt1+pt1=a1Wt1

(1)

a1ct2+a2vt2+pt2=a2Wt2

(2)

两部类按价值计算的利润率不相等，经过竞争形成了一般利润率r，两部类资本家都获得了平均利润：

pt1=(a1ct1+a2vt1)r

(3)

pt2=(a1ct2+a2vt2)r

(4)

t期末总商品产品经过一系列的交换，从卖者手中到达买者手中，形成了t+1期的生产基金和消费基金，简单再生产中只是不断重复(1)(2)式，而扩大再生产不同，第t期各部类的总支出等于第t+1期的资本和第t期的资本家消费之和，必须满足如下关系：

a1ct+11+a2vt+11+(1-e1)pt1=a1Wt1

(5)

a1ct+12+a2vt+12+(1-e2)pt2=a2Wt2

(6)

扩大再生产的实现条件为：ct+12=vt+11+(1-e1)mt1。。价格形式可以表示为：a1ct+12=a2vt+11+(1-e1)pt1，将其带入(5)式可化简如下：

ct+11+ct+12=Wt1

(7)

(7)式是再生产实现条件的通式，同时适用于简单再生产和扩大再生产两种情况。

这里我们仍然采用马克思所论述的“两个相等”条件，表示如下：

at1Wt1+at2Wt2=Wt1+Wt2

(8)

pt1+pt2=mt1+mt2

(9)

(1)-(9)式联立方程组，求解a1，a2，vt+11，vt+12，pt1，pt2，r，e1，e2。

方程组求解：

由(1) (3)式得

(10)

同理，由(2) (4)式得

(11)

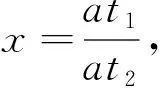
(10)式与(11)式相比得

α1k2x2+(α1-α2k1)x-α2=0

(12)

由(12)式可解得x为常数，只与k1，k2，m'1，m'2有关，代入(11)式可解得

(13)

则r也为常数，只与k1，k2，m'1，m'2有关。

(9)式代入(3)+ (4)式得

(14)

(8) (9)式代入(1)+ (2)式得

a1ct1+a2vt1+a1ct2+a2vt2=ct1+vt1+ct2+vt2

(15)

(15)式代入(14)式得

(16)

(16)式可转化为：

[(k2+1)r-m′2]β=m′1-(k1+1)r

(17)

若(17)式成立，则或者满足情况一：

(k2+1)r-m′2=0且m′1-(k1+1)r=0

或者满足情况二：

(k2+1)r-m′2≠0

若满足第二种情况，则β=[m′1-(k1+1)r]/[(k2+1)r-m′2]

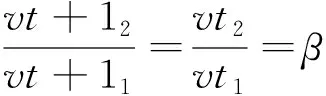
(5)(6)式分别减(1)(2)式得

vt+11=(1+e1r)vt1

(18)

vt+12=(1+e2r)vt2

(19)

两式相比得e1=e2=e

(18)(19)式代入(7)式得

(1+er)(k1+k2β)=α1

(20)

将(13)式求得的r和第二种情况下所求得的β代入(20)式得

其中，λ=k1-k2，α3=k2m′1-k1m'2

(12)(21)两式比较，若要方程有解则必有

(22)

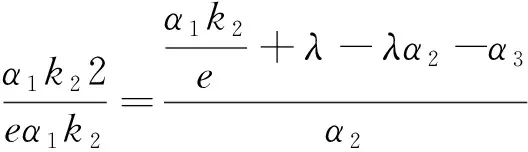
(23)

由(22)式得

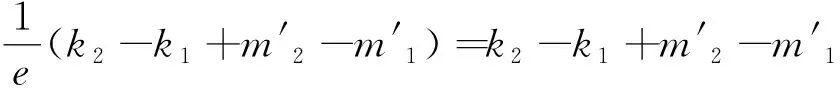
由(23)式得

因为e<1，所以k2-k1+m′2-m′1=0且k2-k1+k2m′1-k1m′2=0

与简单再生产条件下的转形模型所求得的解一样，只有满足这一等式，扩大再生产才存在稳态解。事实上简单再生产模型只是扩大再生产模型在积累率e=0时的特殊情况。此式成立意味着两部类按价值计算的利润率已经相等，不会发生资本跨部类流动，从而不存在价值向生产价格转化的问题。在开始建模时，我们假设两部类按价值交换的利润率不相等，资本从利润率低的部类流出投入到利润率高的部类，通过这样的竞争实现了平均利润率并且保持稳定状态。而我们求解的结果和这一假设矛盾。

四、结论及展望

通过以上这个归谬的过程，可以证明“两个相等”条件不成立。因为从单个部门来看，价值向生产价格转化的现实过程是资本流动导致本部门供求失衡(此处的供求平衡指的是商品按价值交换时的供求平衡)形成新的供求比例，在供求作用下商品按照偏离价值的价格进行买卖。因此，几乎每一个部门都面临着供求失衡，高资本构成的部门供小于求，低资本构成的部门供大于求。在这种情况下，要使得所有部门供求偏离相互抵消，总供求仍然保持平衡，从而总商品产品仍然按价值交换，其可能性微乎其微。稳态模型实际上证明了这种可能性不存在，即“两个相等”不成立。而当“两个相等”不成立时，这种总量分析的思路也难以找到其他更加合理的替代条件，因此这种方案必然行不通。⑩因此，鲍特凯维兹传统的转形问题解决方案是不正确的，必须另辟蹊径解决转形问题。

根据马克思关于一般利润率的论述可知，价值向生产价格的转化只能在社会再生产这个大框架下，通过分析资本流动形成的“一定的供求比例”关系，用单个部类的供求条件代替“两个相等”来说明。解决转形问题必须考虑资本流动，说明一般利润率形成的具体过程。因此，满足“两个相等”条件的静态分析无法解决转形问题，必须进行考虑资本流动、资本竞争过程的动态分析。

注释：

①“两个相等”指的是，价值转化为生产价格后，总利润等于总剩余价值，总价格等于总价值。我们可以把总商品产品看作一个单独的“组合商品”，如果“两个相等”成立，则这个“组合商品”按价值交换，此时总供求平衡。而价值转化为生产价格恰恰是各部门供求偏离的结果。因此，“两个相等”是否成立归根结底就是在各部门都出现供求偏离的情况下能否保持总供求平衡。因为马克思所说的供求平衡指的就是商品按价值交换时的比例。他说：如果供求之间的比例，使某个生产部门的商品总量能够按照它们的市场价值出售，既不高，也不低，供求就是一致的。这是我们听到的第一点。又说：第二点是：如果商品都能够按照它们的市场价值出售，供求就是一致的。参见：马克思恩格斯文集，第7卷[M].北京：人民出版社，2009.184-211.

②比如肯尼思·梅(K·May)认为：马克思使用的计算，主要是用作文字论证的补充说明，他的文字论证将过程和横断面分析结合在一起了，这样的计算即使对今天现有的数学技巧来说，也是做不到的。

③参见：保罗·斯威齐.资本主义发展论——马克思主义政治经济学原理[M].陈观烈,秦亚男,译.北京:商务印书馆,1997.133-143.

④此条件等价于总利润等于总剩余价值。将鲍特凯维兹的三个基本方程相加可得：[(c1x+v1y)+(c2x+v2y)+(c3x+v3y)]r=(s1+s2+s3)z，等式左边表示总利润，右边表示总剩余价值与价格系数z的乘积，当z=1时总利润等于总剩余价值。顺带说明一下，Diaz和Velasco的模型当价格不再变化时和我们的模型一致，但他们所求得的稳态时两部类价格系数之比x=at1/at2不满足方程(12)式。因此，他们的模型必然是有缺陷的。

⑤⑦参见：百年论争——20世纪西方学者马克思经济学研究述要(中册)[M].顾海良,主编.北京:经济科学出版社,2015.720-730.

⑥参见：米克.劳动价值学说的研究[M].陈彪如,译.北京:商务印书馆,1963.132-151.

⑧参见：Emilio Diaz and Francisco Velasco, The Transformation of Values into Prices of Production in Marx’s Scheme of Expanded Reproduction, Review of Radical Political Economics, 2016, Vol.48(3).

⑨参见：沈民鸣.论马克思的两部类价值转形问题[J].政治经济学评论,2008,(01)；沈民鸣.论价值转形与再生产的关系[J].当代经济研究,2016,(01).

⑩参见：丁堡骏.转形问题研究[J].中国社会科学,1999.(05).