M型hBN偏振转化超表面*
高凤伟,隋 超,刘 悦,周 胜
(哈尔滨师范大学)
0 引言
近年来,超材料因其独特的电磁特性使其成为科学研究的热点.超表面是一种人造周期的二维超材料,与超材料相比具有体积小、损耗少、制造容易等优点.超表面在电磁领域有着很广泛的应用(从微波到可见光波段),包括完美吸收超表面、小型谐振腔、新型波导结构、生物分子设备、THz调制、光学传感器等.超表面可以大致分为完美吸收超表面、频率选择超表面、高阻抗超表面、偏振控制超表面等[1].其中偏振控制超表面调控电磁波传输和偏振性质是近期光学研究的热点内容.
电磁波极化在光学和无线电通信中能够发挥巨大的作用,如极化测量、双极化雷达、光纤通信等方面具有重要作用.通过优化单元结构的细节,电磁波可以在反射或透射后转换为交叉极化或其他形式[2].一般而言,偏振旋转器可分为反射型和透射型.反射型偏振旋转器由于其非透射特性而具有相对较高的性能,例如,高效率和宽带宽.对于透射型偏振旋转器,由于不可避免的结构反射,很难同时获得高效率和宽带宽.然而,透射偏振旋转器在实验和工业生产中的应用更为广泛[3].由于极化是电磁波(EM)的最重要特征之一,因此对其进行研究具有重要意义.传统上使用光学晶体和法拉第效应来实现偏振旋转,而这些方法通常需要相当长的传播距离才能获得相位累积,从而导致器件体积大.因此,需要开发厚度小,重量轻的新型旋转装置[4].Zhang 等设计基于经典的三层MMs结构,提出了一种线性偏振转换器,所提出的转换器可以实现从y(x)偏振入射波到x(y)偏振反射波的高效转换[5].Wang等研究提出了一种使用“拼图”策略来独立操纵振幅,相位和极化状态的无源可重构编码超表面.通过手动重新配置编码超表面的布局,可以灵活地控制EM波的属性[6].
双曲超材料作为电磁超材料的重要分支,因其独特的近场调控特性成为研究的焦点.双曲超材料具有双曲色散关系,光学性质与其它材料有很大不同,具有许多新性质.双曲超材料具有高度各向异性,色散关系具有双曲形式,研究频率范围从紫外线到太赫兹.双曲超材料具有近零介电函数和表面声子极化子等性质.双曲超材料研究内容涉及亚波长成像、聚焦、自发等辐射增强,生物传感,热工等方面[7].由于双曲超材料等频色散曲线是双曲型的,可以支持较大的波矢,即在介质内可以传播波长很短的波,因此可以突破衍射极限,在亚波长成像等方面有较多应用.双曲超表面作为一种特殊新型的平面超材料,同样具有双曲色散特性,在理论和应用上也与双曲超材料有诸多相似点.与块体双曲超材料相比,由于纵向维度尺寸的大幅度减小从而将电磁波传播限制在二维平面上,双曲超表面表现出更加优异的性能[8].双曲超表面已经在很多领域得到应用,包括亚波长成像[9-12]、光场局域[13]和增强自发辐射[14]等.
该文提出了一种基于双曲材料六角氮化硼(hBN)的透射型偏振超表面,并对透射率与偏振转化比等性质进行了分析.
1 hBN介电函数
近年来,双曲材料(HMs)的出现带来了一个比较有吸引力的新领域.六角氮化硼(hBN)是双曲材料的一种,对入射波的偏振现象表现出独特的性质.hBN的介电常数包含纵向介电常数εt与横向介电常数εl.hBN的介电常数表示为[15]:
(1)
其中,对于纵向介电常数εt′,ε∞=4.52,ωL0=1610cm-1,ωT0=1360 cm-1, 对于横向介电常数εl,ε∞=4.95,ωL0=825 cm-1,ωT0=760 cm-1,并且τ=5,ω为波数与频率f的关系为ω=f/2πc.

图1 hBN横向介电常数ε1与εt纵向元素图像
hBN的介电常数表现为张量形式如公式(2)所示:
(2)
如图2所示在主轴坐标系xyz中hBN的光轴沿着坐标系的x方向.在实际模拟计算情况中,如果光轴处于其他方向时会影响hBN的偏振与透射性,故该文研究了通过矩阵转换计算改变hBN光轴的方向对偏振性以及透射率的影响.

图2 hBN光轴方向示意图
具体计算方式如下所示在主轴坐标系中先以y为轴顺时针旋转θ角,之后在x′y′z′坐标系中再以z′为轴顺时针旋转α角最后得到光轴在图2中虚线处.介电常数转换计算过程具体如下所示:
ε′=T·ε·T-1
(3)
其中T为转置矩阵,矩阵中各项为xyz-x′y′z′ 坐标系中坐标轴夹角余弦值
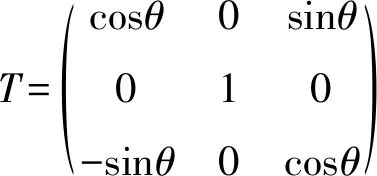
(4)
且
T×T-1=E
(5)
由公式(3)(4)(5)得到
(6)
其中εxx=εlcos2θ+εtsin2θ,εxz=εzx=(εt-εl)×
cosθsinθ,εxy=εyx=εyz=εzy=0,εyy=εt,εzx=(εt-εl)cosθsinθ,εzz=εtcos2θ+εlsin2θ.
同理,再以z′为轴对变换之后的介电常数ε′进行角度为α的转换得到新的介电常数ε″,即
(7)

2 M型超表面结构
该文设计并研究了一种透射型偏振旋转器,实现了入射TE波或TM波到透射光转变为椭圆偏振光或者圆偏振光.设计hBN的位型如图3所示,由一个正方形的hBN与一个“M”型的凹槽组成.其中hBN的厚度d为1 μm,边长为2 μm.“M”型凹槽中dml为0.2 μm,lm1为1.2 μm,凹槽的深度Hm1=d为1 μm与hBN的厚度相同,其中“V”字形凹槽的深度Hm2为0.5 μm.

图3 (a)超表面单元结构图 (b)“M”字形结构图
3 结果分析与讨论
首先研究TE或TM波入射时光轴角度α对超表面透射率与偏振特性的影响.超表面的结构如图3所示,对上述结构分别计算了透射率随着入射波频率与角度α改变而变化的情况,以及入射波频率和不同入射光对透射率的影响.入射波的频率范围是1.40~1.80×1014Hz,角度α的范围是0°~180°.
3.1 超表面透射率
图4(a)与图4(b)分别为TM与TE波入射时的透射率,如图所示1.40~1.55×1014Hz频段内时透射率比较低, 1.55~1.80×1014Hz频段内透射率比较高.并且在两个频率范围内有一条明显的分界线,造成透射率差别比较大的主要原因是介电常数εl大小在近零区域的变化.从图1中可以看到当εl<0时透射率比较低相反当εl>0时透射率比较高.从图4(a)中可得在1.55~1.80×1014Hz频段内α=1.6 rad时,透射率最大达到0.75且当α>1.4 rad时随着角度的增大透射率减小,α<1.4 rad时随着角度的减小透射率显著减小.在图4(b)中当α>2.6 rad时随着角度的增大透射率增大,α<0.6 rad 时随着角度的减小透射率逐渐增大,透射率最大值为0.79,这说明主光轴改变角度α对透射率的影响比较大.另一方面,从图4(a)及图4(b)中可以看出在1.4~1.55×1014Hz频段内透射率很小,不同的是在图4(a)中当α>1 rad和α<2.4 rad时透射率基本为零而在图4(b)α<0.8 rad或α>2.4 rad时透射率基本为零.以上的现象说明所设计的超表面在这个频段内对线偏振光的传播具有很强的阻碍作用,并且随着α的改变会对不同入射光产生不同的阻碍作用.

图4 (a)(b)分别为TM波入射和TE波入射时的透射率
3.2 超表面偏振转化比(PCR)
电磁波的极化状态可以分为线性极化、圆形极化和椭圆形极化,是电磁波的基本特性.操纵电磁波的偏振状态,如线性极化旋转及线性极化与圆/椭圆形极化之间的转换,在光学传感、通信等方面具有重要的作用.偏振转化具有描述线性极化转换为圆/椭圆形极化的转换效率的意义.PCR的取值范围是0~1,且所得结果越接近1说明转换效率越高.但当PCR=1时说明产生了90°的线性极化旋转,其它情况时则是线性极化转换为圆/椭圆形极化.其公式为[16]
(8)

图5 (a)(b)分别为TM波和TE波入射时偏振转换比
图6(a)(b)(c)(d)在COMSOL中模拟计算的电场图,其中需要注意的是图6(c)(d)中上下两侧是模拟中的空气层,中间为超表面结构、图6(a)(b)入射光为TM波频率为 1.602×1014Hz且光轴角度为1.6 rad时超表面的电场图,图6(c)(d)入射光为TE波频率为1.602×1014Hz且光轴角度为0 rad时超表面的电场图.从图4(a)(b)中可以看出此时的透射率值最大分别为0.75与0.80.从电场图中可以看到在“M”型结构两侧的电场局域化比较强,中间结构电场局域化比较弱,所以超表面“M”型结构的设计有效提高了单层超表面偏振转化性质与透射率.

图6 (a)(b)分别为TM波入射使超表面电场俯视图和侧视图,(c)(d)分别为TE波入射使超表面电场振幅俯视图和侧视图
4 结论
该文设计了单层六角氮化硼(hBN)透射型偏振转换超表面,研究了不同频率、不同入射偏振光以及改变hBN光轴对透射率和偏振转化比的影响.利用有限元软件COMSOL进行仿真模拟,研究结果表明当TM波入射时,在1.55~1.65×1014Hz频率内透射率为0.4~0.5偏振转换比为0.5~0.7.当TE波入射时,在1.40~1.55×1014Hz频段内偏振转化比为0.6~0.9.此外研究了光轴处于任意方向时对透射率及偏振转化比的调控.该文设计的超表面实现了高效率的偏振转换比,在光学传感、隐身技术、通信等方面具有重要的应用.

