基于因子分析对小微企业信贷风险评价及信贷策略规划 *

谢 睿，王鸿铭，王昱璇，朱家明

(安徽财经大学)

0 引言

随着中国经济的快速发展和经济结构的不断调整，作为数量最多且创新性最高的小微企业需要大量资金进行转型升级.小微企业规模较小，且缺少可抵押的资产，因此银行借贷往往是小微企业重要的资金来源.银行通常会通过企业的盈利能力、偿债能力以及信誉评价等来为其提供相应的贷款政策.例如：偿债能力较强、信誉较好的企业可以得到较为优惠的贷款利率和较长贷款期限，而实力较弱、偿债能力不强且信誉较差的企业很可能无法贷款或贷款利率较高.因此，银行根据小微企业的各项交易指标和影响力等因素去评价企业的风险指数对于银行做出正确的信贷决策来说十分重要.

郭妍通过构建Logit回归模型和LDA多元判别分析模型对中国小企业信贷风险进行实证度量，得到企业违约的预测情况[1].但文章的模型预测准确率不是很理想，数学模型精度不够.杨立娟通过主成分分析法提取主成分变量，并建立Logit回归模型对模型进行回归分析和拟合优度检验，从而构建了小企业信贷风险评估模型[2].但选取的评价指标中忽视了非财务指标对于企业经营情况的影响，评价指标选取不全面.赖轩诚将财务杠杆与Z-Score模型相结合，以乐视为例，建立财务风险评价模型，依此评价企业的经营水平和偿债能力[3].但模型没有很好的计量企业的表外信用风险且缺乏对违约和违约风险的系统认识.宋泽朋通过独立T检验方法筛选指标并建立指标体系，基于BP神经网络建立银行信贷风险评价模型，但指标的构建存在一定的局限性[4].王梦来通过实证研究得出KMV风险评价模型适用于大规模上市公司，而不适用于小规模上市公司，对小微企业的信贷风险评价而言还存在一定的局限性[5].

对于银行来说，对贷款企业进行综合性评价可以帮助银行更好的了解企业的偿债能力，以做出较为高效的放贷决策.对于社会来说，将社会多余资金用于发展势头较好、信誉较高的企业也会提高社会资金的使用效率，更大程度的促进国民经济的发展.对于企业而言，经营状况良好且企业信誉较高即可以获得较高的贷款额度和贷款优惠，促进企业发展的良性循环，也可以在一定程度上激励企业积极承担社会责任，促进企业的经济发展.

1 小微企业信贷风险评价体系的构建

1.1 指标体系构建

根据企业信贷风险的相关理论，结合小微企业发票的特点以及数据的可获得性，选取了7个指标，构建企业信贷风险评价指标体系，见表1.其中：考虑到季节性波动，采购能力为各企业2018～2019年度各半年度进项发票的价税合计平均值，销售能力为各企业2018～2019年度各半年度销项发票的价税合计平均值，盈利能力为企业应纳税额，即销项税额与进项税额之差.信誉评级为银行对各企业的信誉等级并依据中国工商银行对企业的信誉等级划分依据进行量化.进项稳定性指标为各企业进项发票数目与供货方数目之比，数值越大证明供货方稳定性越大，销项客户稳定性为各企业销项发票数目与采购方数目之比，数值越大证明客户稳定性越大，退货比例为销项发票中为负值(退货)所占总的销项发票的比例.

表1 小微企业信贷风险评价指标体系的构建

1.2 数据来源与假设

该文数据来源于2020年全国大学生数学建模竞赛C题提供的123家有信贷记录企业的相关发票数据以及302家无信贷记录企业的相关发票数据；为了便于研究特提出以下假设：(1)银行基于利润最大化为小微企业制定贷款策略；(2)所给发票数据为企业在其时间段的所有发票数据；(3)银行和企业均具有一定的风险承受能力；(4)所有企业均中国工商银行的量化标准对信誉评级进行量化.

2 123家小微企业的信贷风险评级与信贷策略的制定

2.1 研究思路

该文将选取123家企业的财务指标和非财务指标构建指标体系，通过因子分析法筛选显著性较强的公因子并确定相关指标的权重，建立综合评价模型，通过该模型评价小微企业信贷风险.跟据评价结果从银行获得利息最大化的角度建立信贷分配方程组，通过MATLAB求出最优解.

2.2 研究方法

因子分析模型，克服了截面数据随机性的问题，从复杂繁多的指标中提取若干个主要的公因子，通过公因子来反映原始指标，再计算相对方差贡献率作为所提取的公因子的权重，最后计算综合得分与排名，通过不同的公因子的得分以及总得分来综合反映企业信贷风险的情况.

2.3 模型的建立与结果分析

根据所建立的指标体系，使用 SPSS 软件对模型进行计算求解.

(1)适应性检验

在进行因子分析时，需要对数据进行可行性检验且通过检验，因子分析的结果才具有可信度.通过 SPSS 分析得到数据可行性检验的结果，见表2.通常适合进行因子分析的数据在进行检验时，KMO 值大于0.5，变量间的偏相关系数远小于简单相关系数，检验结果的 KMO 值为0.635( >0.6) ，适合用于因子分析.Bartlett’s 球形度检验对应的P值为0.000(0.000<0.001),说明在99%的置信水平下拒绝原假设，变量间有着较强的相关关系，所选指标适合进行因子分析.

表2 KMO 和巴特利特检验

(2)提取公因子

根据公因子方差表，反映了各个原始变量被提取的信息，其中大部分指标都被提取了 90%左右的信息，说明原始变量的绝大部分信息都被保存下来，所建立的模型可以反映企业信贷风险的基本情况.

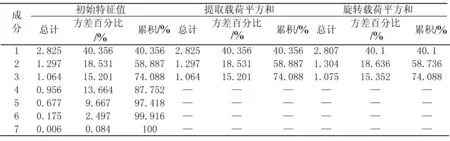
在文中，根据碎石图所提取3个公因子，方差贡献率分别为40.100% 、18.636%和15.352% ，累计方差贡献率达到74.088%，见表3.因此，保留前3个公共因子就能保留原始变量的绝大部分信息.

表3特征根与方差贡献率

(3)公因子的命名

使用最大方差旋转法进行因子旋转，简化因子结构，使得公因子的实际含义更加清晰.旋转后的成分矩阵见表4，第一个公共因子在采购能力、销售能力、盈利能力上有较大载荷，反映企业基本经营状况，故命名为企业经营能力因子，第二个公因子在信誉评级、进项客户稳定性有较大载荷，反映企业信誉情况，故命名为企业信誉因子.第三个因子在退货比例、销项客户稳定性上有较大载荷，反映销售稳定性情况，故命名为企业销售稳定性因子.

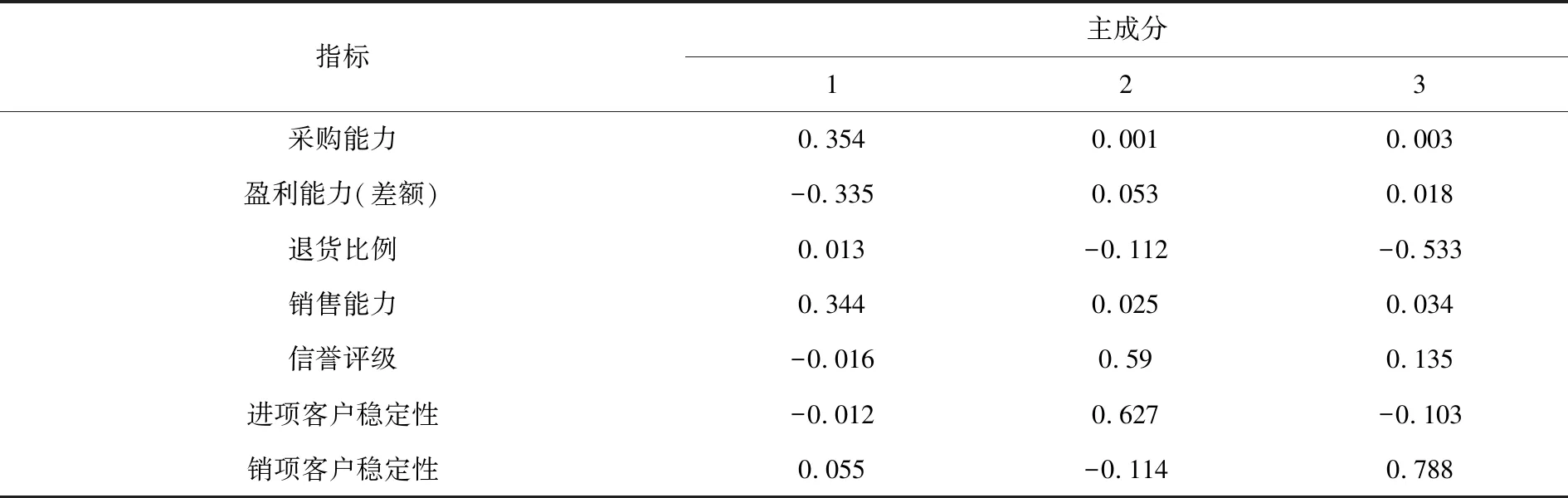
表4 成分得分系数矩阵

(4)企业信贷风险评级及排名

将公因子各自的方差贡献率除以累计方差贡献率，即可计算因子旋转后的相对方差贡献率，企业经营能力因子、企业信誉因子、企业销售稳定性因子的相对方差贡献率分别为54.12%、25.15%、20.73%从而作为权重进行赋值.

根据成分得分系数矩阵，计算企业经营能力因子、企业信誉因子、企业销售稳定性因子的得分函数

(1)

(2)

(3)

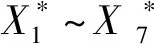
通过计算出的相对方差贡献率得到综合得分函数:

Y=0.5412Y1+0.2515Y2+0.2073Y3

(4)

求解得出各企业综合得分并排名，见表5.

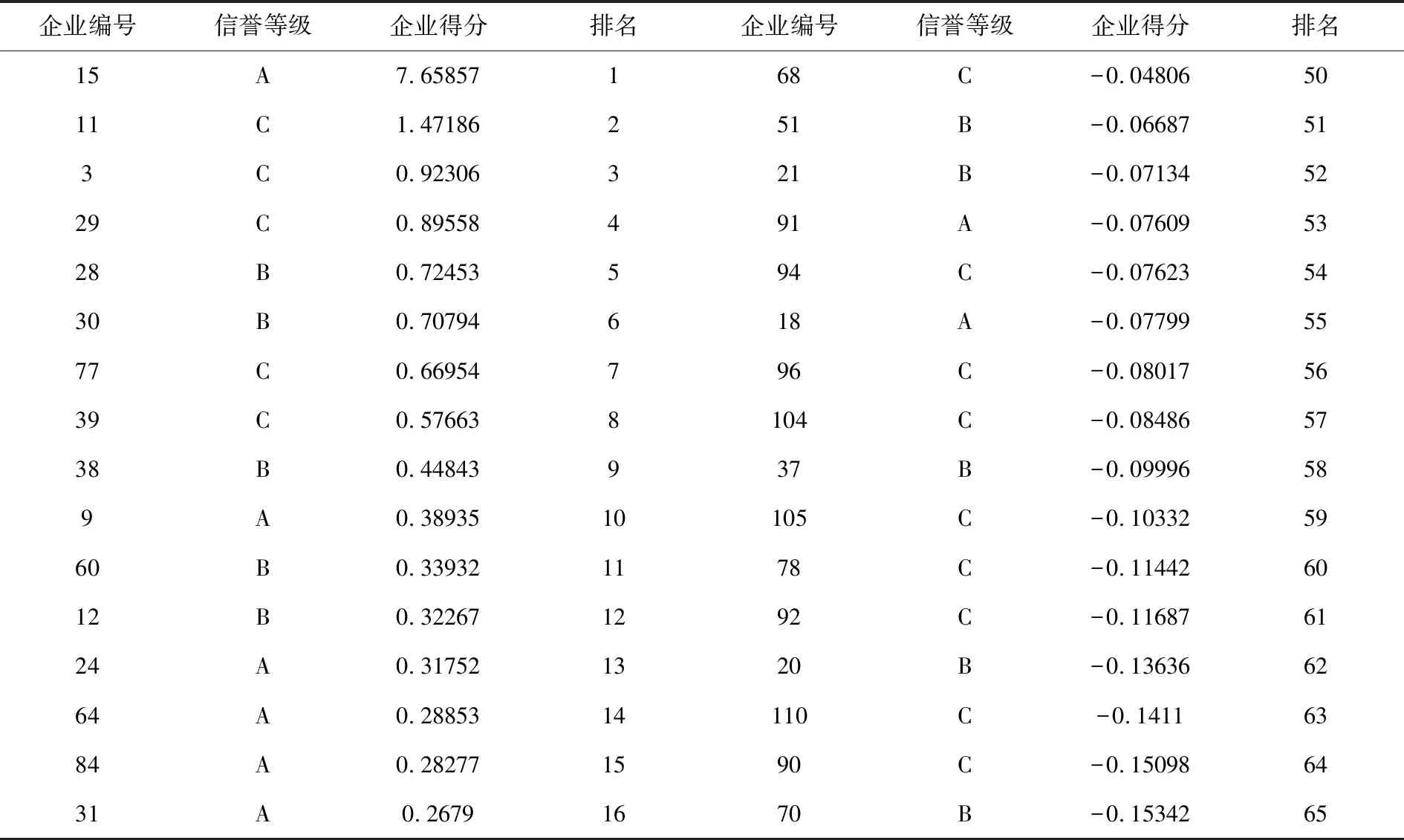
表5 123家企业信贷风险排名

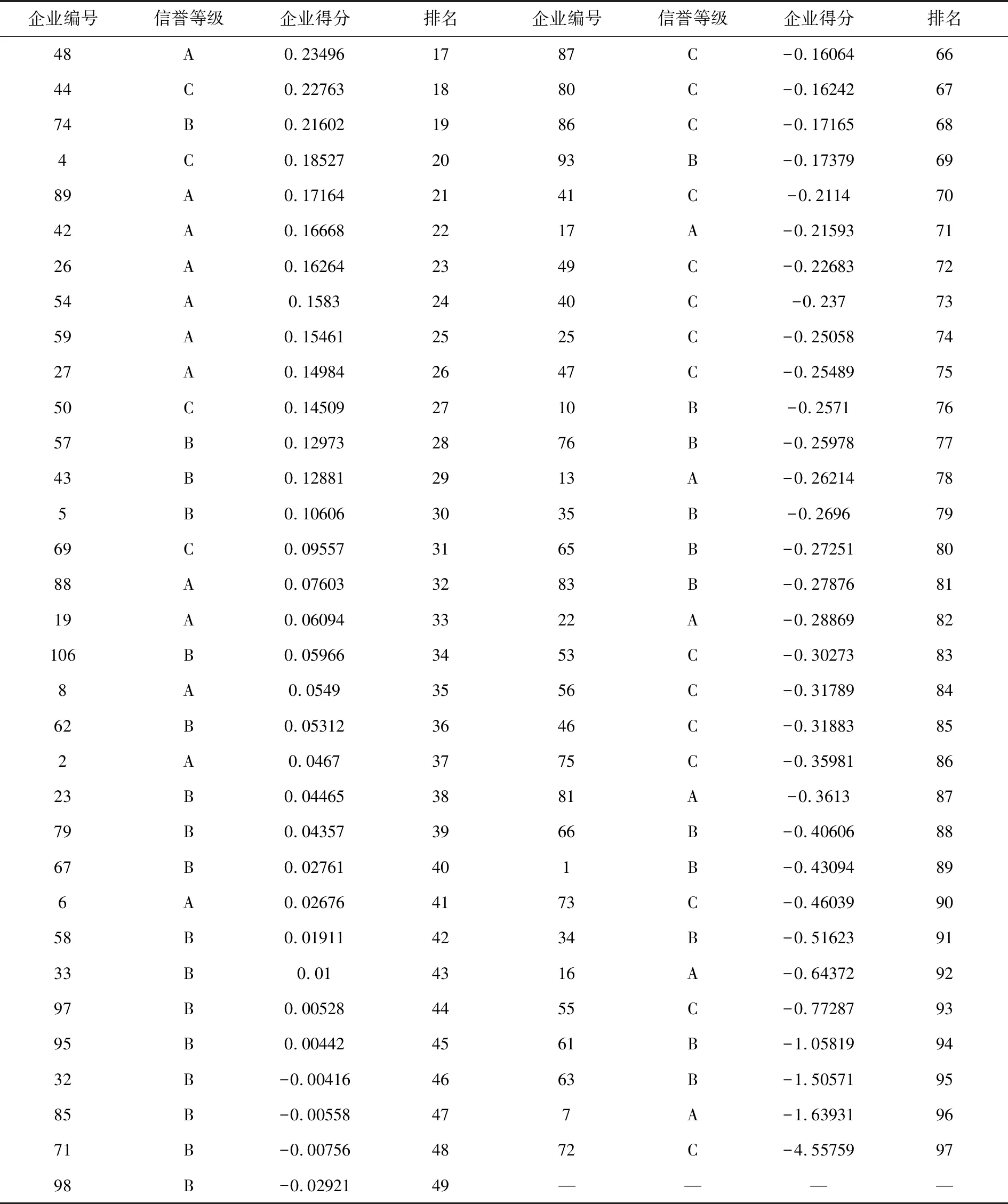
续表5

(5)银行信贷策略的制定

在对各个企业进行信贷风险综合评价后，需要根据此对企业的放贷额度进行高效分配.在分配的过程中，已知银行放贷金额为固定值,银行会根据每家企业的信贷状况和风险评级做出相应的利率和放贷额度的决策.

首先银行放贷固定额为F，银行分配到每个企业的贷款额度为ui，结合银行利率与客户流失率的表格综合计算银行的最终受益，建立保证银行最终受益最大化的线性规划方程组：

在上述方程组中，函数(5)表示银行信贷总额度为一个固定值，函数(6)表示企业的信贷风险率与综合评价值之间的关系，函数(7)表示银行年利率与客户流失率之间的相关关系.

综合银行放贷风险与放贷收益，得到以下函数：

(8)

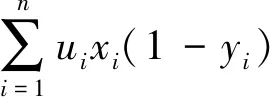
分析银行贷款年利率与客户流失率的数据之间的关系，发现两者之间呈线性关系.因此采用最小二乘法对方程进行拟合，得到以下结果：

yA=7.13104x-0.05276

(9)

yB=5.96598x+0.02850

(10)

yC=6.07206x+0.00969

(11)

ti为运用因子分析法得出的企业评分，用以求得年利率：

(12)

将银行给出的年利率Xj与估计年利率xi进行对比，对∀x∈{xi},∀X∈{Xj}，当|xi-Xj|达到最小值时，令:

xi=Xj

(13)

根据xi=Xj的对应关系，求得97家企业划分8级利率.

根据97家企业求值结果，将银行贷款额度分配分为三个等级，即Ⅰ、Ⅱ、Ⅲ级，每级具体信贷策略见表6.

表6 银行贷款额度分配策略

银行可根据以上等级为小微企业确定贷款年利率，而贷款额度将利用上述W的函数方程，利用线性规划求解最终求得各个企业所对应的贷款额度.

3 302家无信誉评级的小微企业的信贷风险评级与信贷策略的制定

3.1 研究思路

使用神经网络算法，将123企业相关数据作为 BP 神经网络的训练样本，建立 BP 神经网络预测模型.302家企业的信誉评级问题依旧满足问题二中的约束条件，通过预测可得到302信誉评级情况.

在获取神经网络学习结果后同样通过因子分析法确定指标权重，计算得分，评价小微企业信贷风险.并根据评价结果建立信贷分配方程组，求解最优信贷策略.

3.2 研究方法

BP(Back Propagation)神经网络是一种按误差逆传播算法训练的多层前馈网络，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小.BP 神经网络模型拓扑结构包括输入层、隐含层和输出层(如图1所示)，具有良好的自适应性和分类识别等能力.神经网络可以看作是一个函数映射，适用于有明确的输入与输出的对应关系，但其中的函数不容易确定问题.而含企业信誉等级的预测可以看成将其除信誉等级外的指标数据作为输入，企业信誉等级为输出的复杂函数映射问题.因此，可以利用BP神经网络作为企业信誉等级进行预测.

3.3 模型的建立与结果分析

(1)企业信誉等级的预测

经过异常值剔除和归一化等预处理之后，总共有113家企业的指标量可作为学习训练的样本，剩余10家企业的数据作为验证的样本即：训练集为前113家企业的信誉等级数据，验证集为后10家企业的数据.

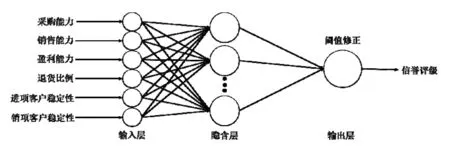
图1 BP神经网络结构示意图

由BP神经网络模型预测结果可知:预测值与实际值比较接近，局部搜索特性和收敛速度快，预测结果精确度较高.因此对302家无信誉评级的企业进行信誉评级，经实验结果，有58家企业信用为D，原则上不予放贷，因此筛选出244家企业进项数据处理.

(2)信贷风险的评定

根据所建立的指标体系以及BP神经网络对244家企业的信誉评级，使用SPSS软件对模型进行计算求解.

表7 成分得分系数矩阵

根据成分得分系数矩阵(见表7)，计算企业经营能力因子、企业信誉因子、企业销售稳定性因子的得分函数.并通过计算出的相对方差贡献率得到综合得分函数求解得出各企业综合得分并排名，见表8.

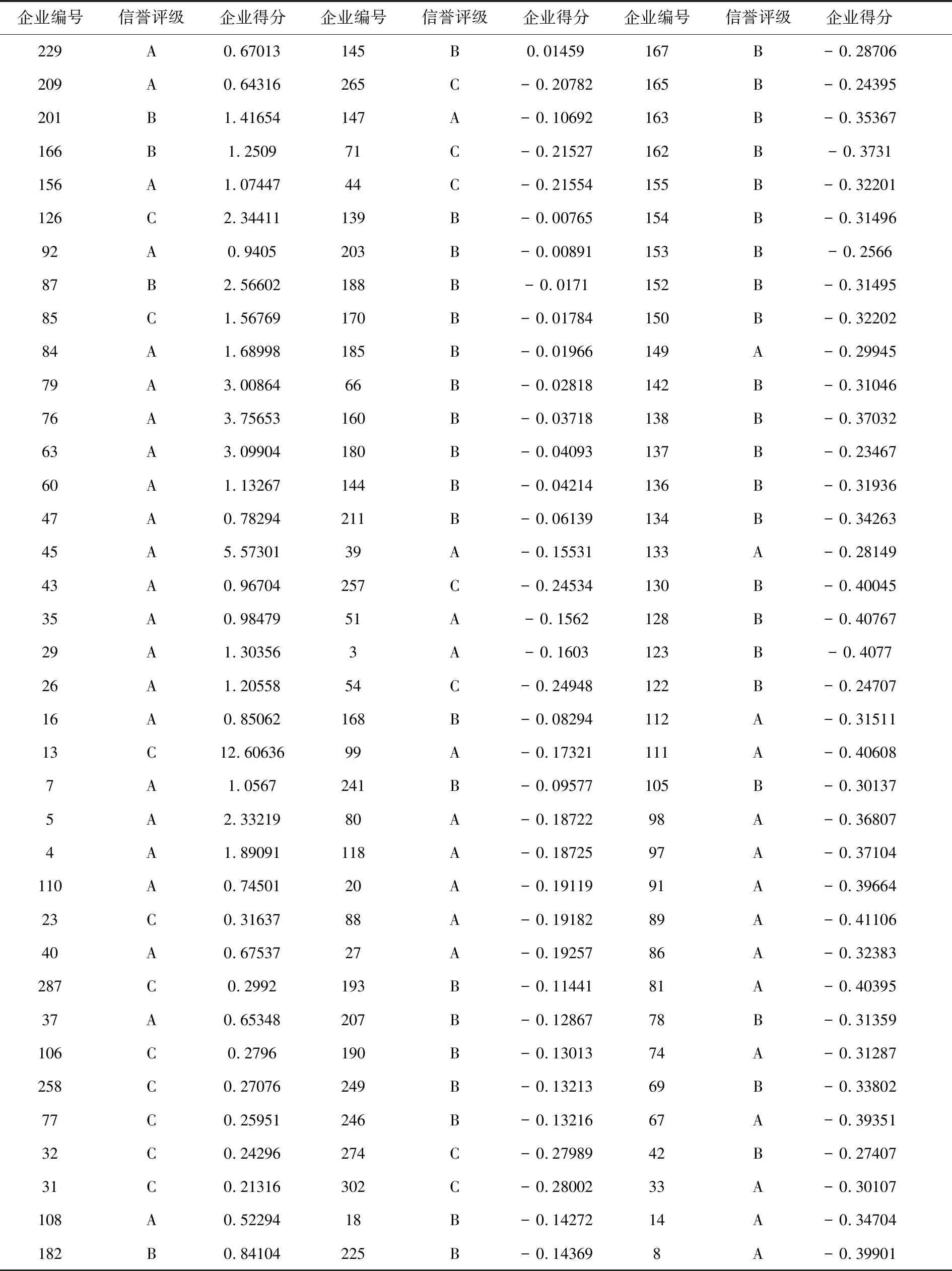
表8 302家企业信誉评级与信贷风险得分

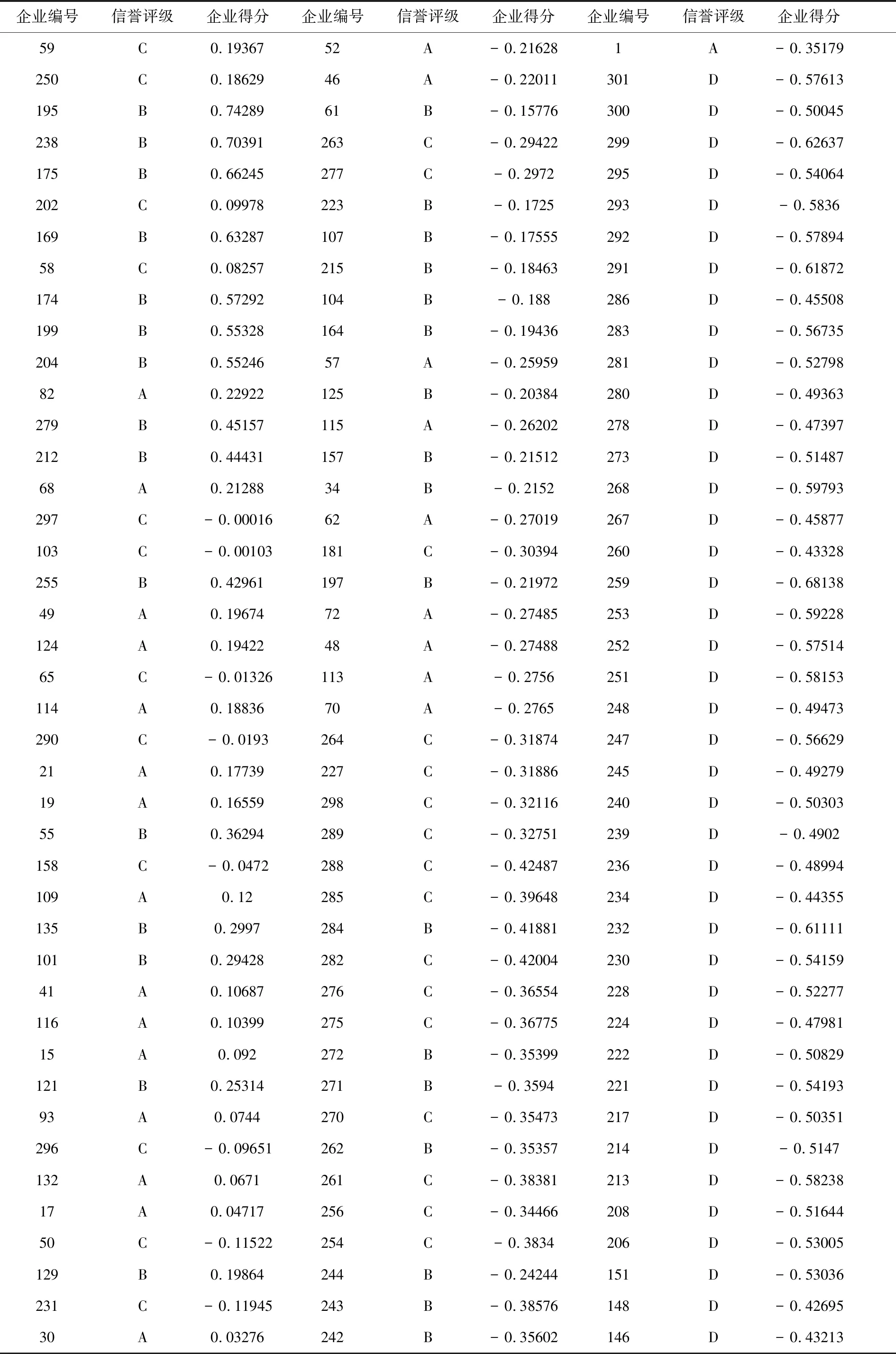
续表8

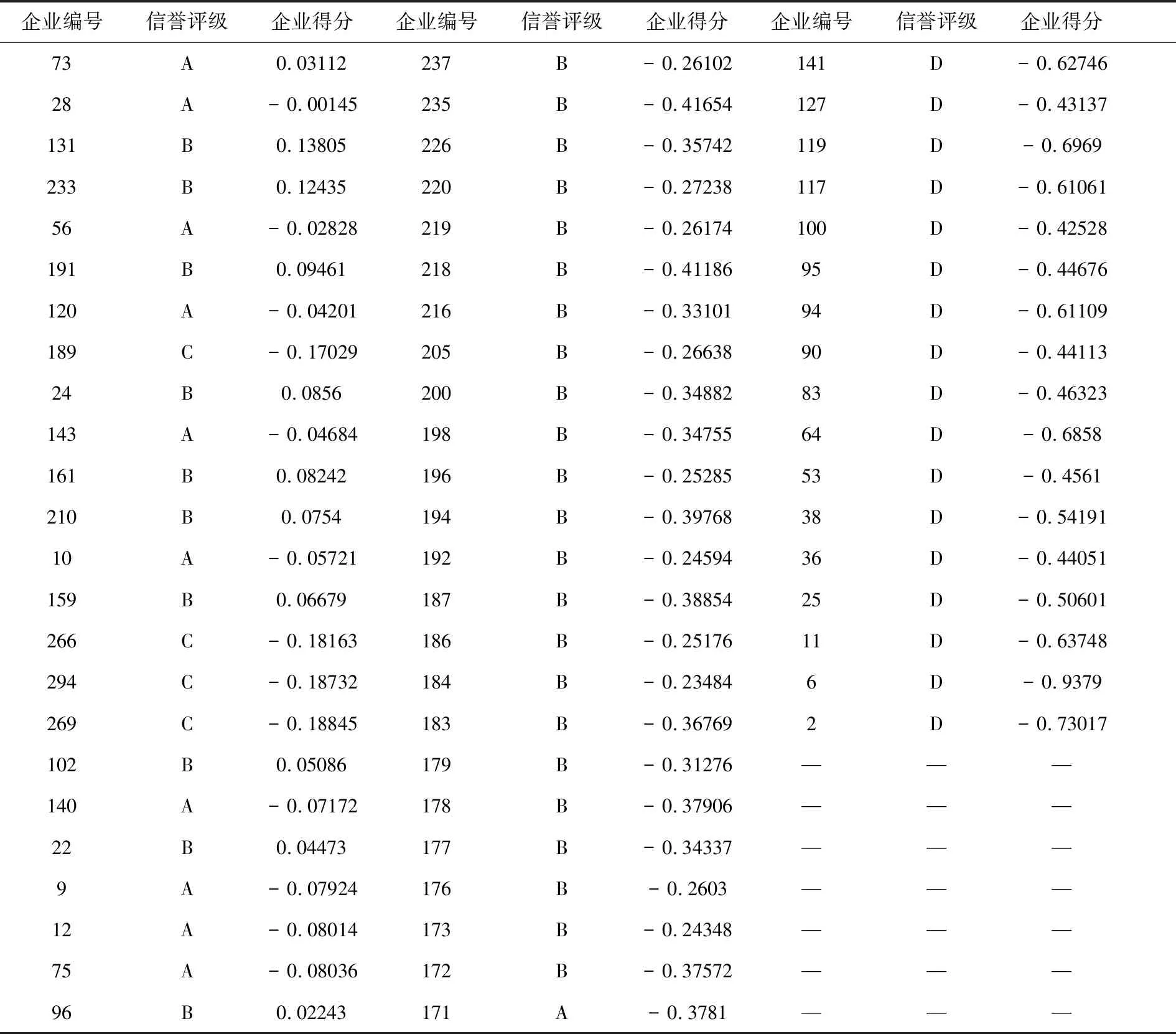
续表8

(3)银行贷款的分配

在对该302家企业进行信贷风险综合评价后，需要根据此对企业的放贷额度进行高效分配.

同样建立多目标规划模型，假定银行放贷固定额为F，银行分配到每个企业的贷款额度为ui，结合银行利率与客户流失率的表格来综合计算银行的最终受益，建立银行放贷风险与放贷收益函数：

(14)

利用Lingo软件进行求解，把求得的年利率按照银行年利率分类.

确定各个企业的贷款利率后，带入到信贷风险评级公式中，利用线性规划求得各个企业是否贷款以及贷款策略的最优解.

4 结束语

为了更好的帮助银行做出较为高效的放贷决策，该文根据已知各个企业的交易发票数据和信誉状况对123家有相关信贷记录的企业的信贷风险进行量化分析并依据此给出银行对于各个企业的信贷策略；在上述评价模型的基础上，对302家无信贷记录的企业进行信贷风险指标量化分析，并给出信贷分配策略.

该文在所提供数据的多个角度挖掘出七个指标，构建了企业信贷风险评价指标体系.尽管由于数据有限，企业的资产负债能力、现金流状况等指标无法列入到评价指标体系中，可能造成评价模型的最终结果与企业实际状况出现些许误差.但该风险评价体系在一定层面上可以反应企业的信贷风险评价，还可以应用于银行对企业的偿债能力、稳定经营能力等多个角度的分析判断，有利于银行信贷业务的发展.而逐步深入、层层递进的多目标规划模型不仅可以合理规划银行放贷额度，还可以应用于企业或银行在进行投资过程中的风险评判和投资额度规划的问题中，保证收益的最大化.