气体静压轴承相位致振气锤失稳机理与试验

马 伟，孔祥龙，徐 毅，朱 敏，赵雄浩

(上海卫星工程研究所， 上海 201108)

1 引 言

在气体静压轴承的工程应用之初，气体静压轴承的气锤振动现象[1]即被发现并引起关注。国内外学者在研究其静态特性[2-5]的同时，开始探究发生气锤自激振动现象的原因,以及能够有效避免产生气锤自激振动的方法。Powell[6]和Grossman[7]等人在其著作中均有关于气体静压轴承中气锤振动形成机理及抑制措施的相关论述。一般来说，气体静压轴承的气锤振动是由于气体的可压缩性、压力变化滞后以及惯性耦合引起的一种自激振动[8]。国内外学者分别从气体容积填充延迟[9]、挤压和容积效应[10]、振动做功[11-12]、涡流振动[13]以及气流噪声[14]等角度对气体静压轴承气锤失稳的原因进行了解释，在一定程度上揭示了轴承气锤失稳的工作机理，为气体静压轴承气锤失稳的定量研究提供了相关理论指导。

在上述对气体静压轴承气锤失稳机理认识的基础上，目前国内外主要形成了诸如稳定判据法、图解法、动态刚度和阻尼法以及实验法等分析方法。稳定判据法是通过建立轴承运动单元的动力学模型，在运动方程基础上运用小参数摄动方法以及连续性条件，由Routh-Hurwitz稳定性判据获得气体静压轴承中气锤振动稳定判据的解析分析方法[15-16]。稳定判据法可快速判断所设计的气体静压止推轴承在特定参数下是否会发生气锤振动，便于工程应用。但该分析方法为解析分析方法，不能获得气膜厚度与动态压力之间的相位关系，并且不能反映轴承质量对气锤自激振动的影响。图解法是将振动微分方程的分析结果表示为时间与位移的关系，或位移和速度与时间的关系，并通过图解的方式表现[17-19]。图解法由振动基本理论出发，通过位移直观反映稳定特性，易于进行实验验证，可用于气体轴承气锤自激稳定的定量研究。但目前仍主要用于气体静压轴承气锤振动的定性分析。动态刚度和阻尼法通过参数摄动法，使气体静压轴承在平衡位置附近进行小幅简谐运动，获得了以静态气膜压力为变量的稳态压力分布和以动态气膜压力为变量的动态压力分布。动态气膜压力的实虚部在整个气膜区域的积分分别为气体静压轴承的动态刚度和阻尼，进而可以在频域角度上分析气体静压轴承的稳定性[20-23]。动态刚度和阻尼法为定量研究方法，可获得气体静压轴承在频域上的振动特征，但该方法无法直观判断气体静压轴承是否发生气锤振动，亦无法获悉气锤振动的阈值。对于气体静压轴承的气锤振动，一些学者由实验角度出发，分析了气体静压轴承的气锤振动产生原因和参数影响[24-26]。上述理论和实验研究方法用于气体静压轴承的气锤失稳参数化影响分析，并基于此提出如降低供气压力、减小节流孔径等一些抑制气锤失稳的技术措施。

随着超精密装备中运动速度和运动精度的不断提升，在静态特性满足性能要求的基础上，气体静压轴承的动态特性对超精密装备整体性能的影响日益严重，并成为气体静压轴承机理研究和工程应用中的热点和难点问题[27-28]。目前，气体静压轴承中气锤振动的产生原因为：由于轴承间隙改变时，气体容积发生变化，而容积内的气体质量不能瞬间达到平衡时所需的量值，两者在时间上的不同步以及惯性耦合引起了气锤自激谐振。通过上述的研究分析可以发现，目前对于该时间不同步引起失稳的机理研究较少，如果可以通过外部激励，人为改变相位差，则可以成为抑制气锤振动的一种新的方法。因此，本文从相位角度开展气体静压轴承的气锤失稳机理分析，并用于指导气体静压轴承气锤失稳抑制方法研究。

2 气体静压轴承相位致振理论建模

2.1 气体静压轴承分析模型

为了研究气体静压轴承发生气锤失稳过程中，轴承间隙与压力变化的相位关系，以如图1所示的气体静压轴承结构开展研究，其轴承的结构参数如表1所示。

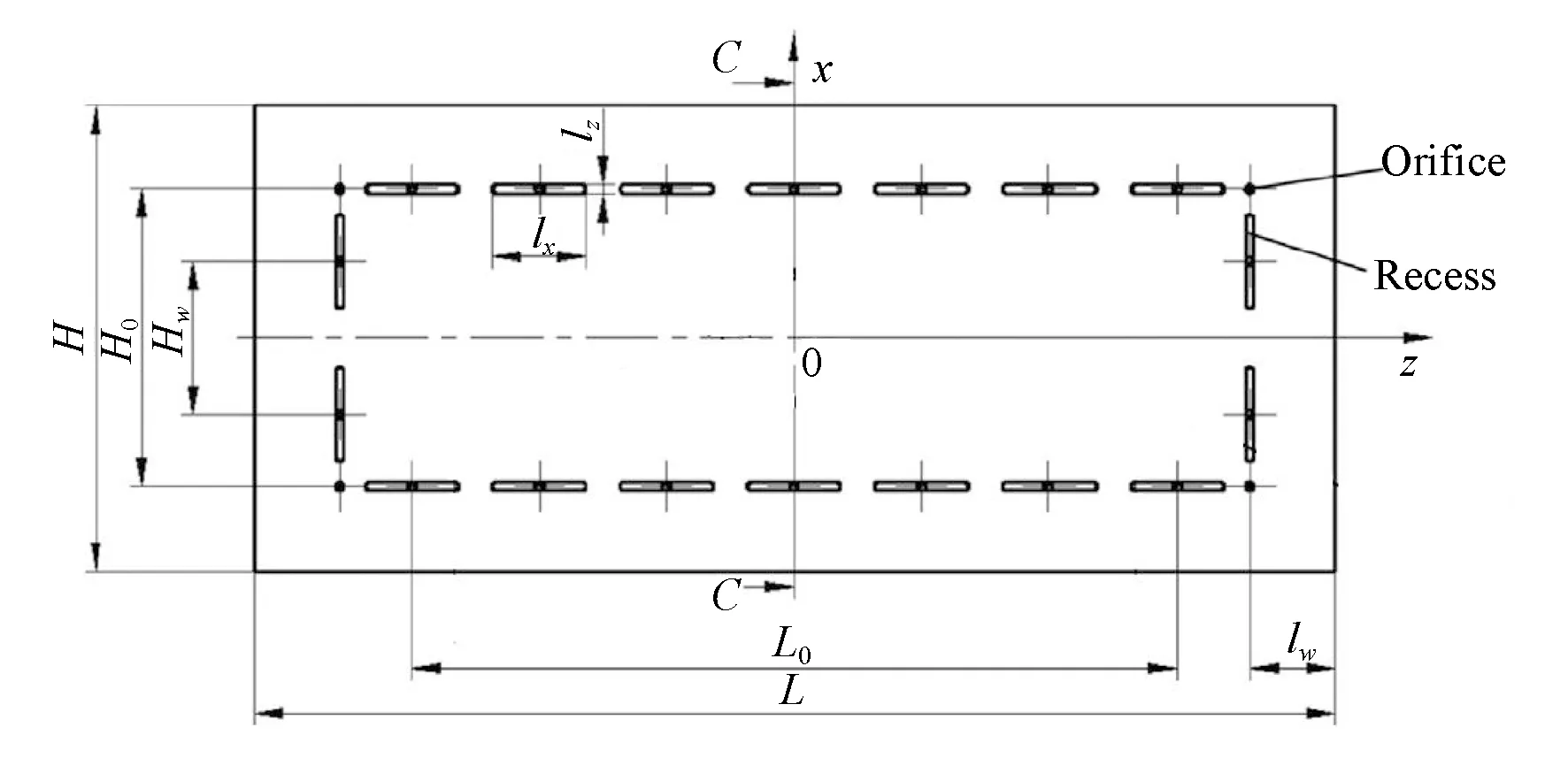
图1 气体静压轴承结构示意图Fig.1 Structure diagram of aerostatic bearing

表1 气体静压轴承结构参数

Tab.1 Structure parameters of aerostatic bearing

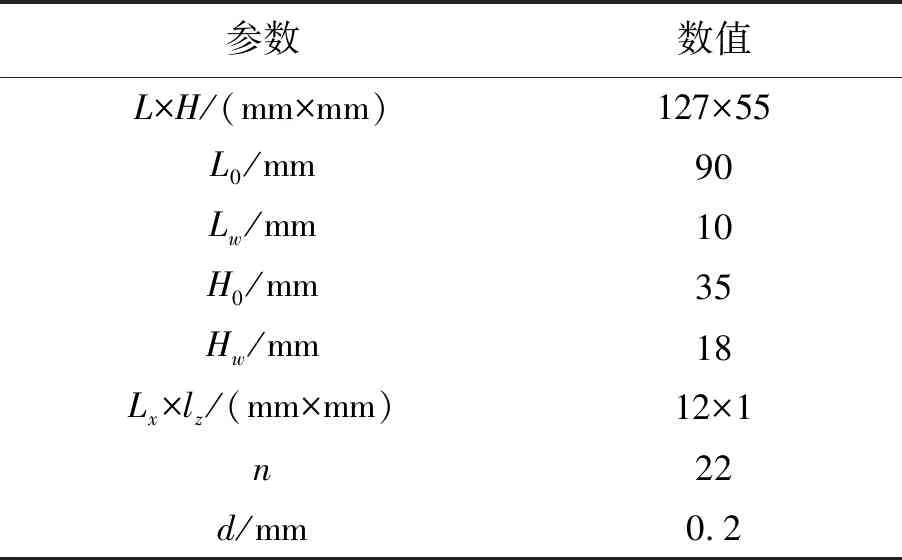
参数数值L×H/(mm×mm)127×55L0/mm 90Lw/mm 10H0/mm 35Hw/mm 18Lx×lz/(mm×mm)12×1n22d/mm 0.2

2.2 气体静压轴承相位致振建模

用于分析气体静压轴承动态特性的通用雷诺方程如下：

(1)

节流孔处流量为：

mci=12ηΔipdi,i=1,2,...,n.

(2)

当含有均压槽时，均压槽内的质量流量变化率为:

(3)

节流孔流入流量为：

(4)

因此，包含节流孔和均压槽的雷诺方程为[10]：

(5)

其中:h为气膜厚度(m)；pdi为节流孔出口压力(Pa);p为 气体压力(Pa);η为空气黏度系数(Ns/m2);t为时间(s);pa为环境压力(Pa);u1u2为x方向气体速度(m/s);w1,w2为y方向气体速度(m/s);v为节流孔出口平均速度(m/s);pa为空气密度(kg/m3);Δik为节流孔出深度(m);Δ0ik为均压腔深度(m)。

利用加辽金加权余量法对式进行数值离散，待求解的离散化形式的含挤压效应和容积效应的改进雷诺方程为：

(6)

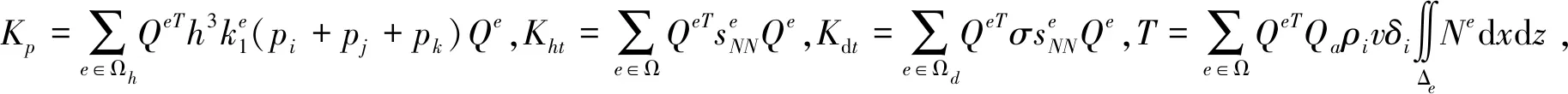
(7)

由气体静压止推轴承的运动方程为：

hM=F-gM.

(8)

令系统状态:

x1=t,x2=h,x3=h,x4=p，

(9)

则气体静压轴承振动的状态方程为:

(10)

由式(10)可以获得气体静压轴承的静态特性和动态特性，以及气体静压轴承动态过程中，气膜厚度和承载之间的相位变化关系。

3 气体静压轴承相位致振数值分析

3.1 气体静压轴承分析模型

本文采用有限元方法研究气体静压轴承的动态特性数值分析。考虑结构的对称性和边界条件，仅对气体静压轴承的1/4轴承进行分析，计算网格如图2所示。其中Sa是环境边界，Sp是对称边界,Sr是均压槽边界,Sz是节流孔边界。 采用三角形单元体，均压槽忽略其宽度采用线性气源假设。

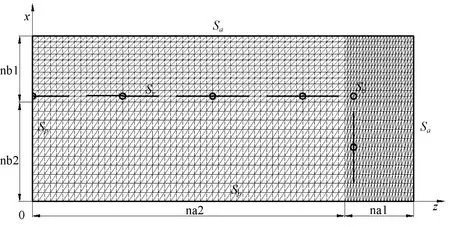
图2 气体静压轴承有限元网格划分Fig.2 Computational meshes of aerostatic bearing

边界条件如下：

在环境边界：

p=pa.

(11)

在对称边界：

(12)

在节流孔和均压槽边界：

p=pd.

(13)

利用MATLAB进行数值求解，求解流程如图3所示。

图3 数值分析流程图Fig.3 Flowchart of numerical analysis

图4 气体静压轴承压力分布Fig.4 Pressure distribution of aerostatic bearing

3.2 气体静压轴承分析结果

当供气压力为4×105Pa且气膜厚度为30 μm时，气体静压轴承的压力分布如图4所示。

由图4可以看出，在节流孔附近出现压力峰值，在均压槽附近，通过均压槽的压力均化，压力分布均匀性好。因此，该分析可以获得气体静压轴承在特定工作参数下的准确压力分布。在此基础上研究不同工作参数下，气体静压轴承的气膜厚度随时间的变化情况，分析结果如图5和图6所示。由图可知，当供气压力为4×105Pa且初始气膜厚度为25 μm时，气体静压轴承的气膜厚度随时间的变化表现出大幅值状态为气锤失稳状态，在气膜厚度为33 μm时，气体静压轴承的气膜厚度随时间的变化呈现出运动稳定状态，因此，该方法可以辨识出气体静压轴承的动态运动状态。

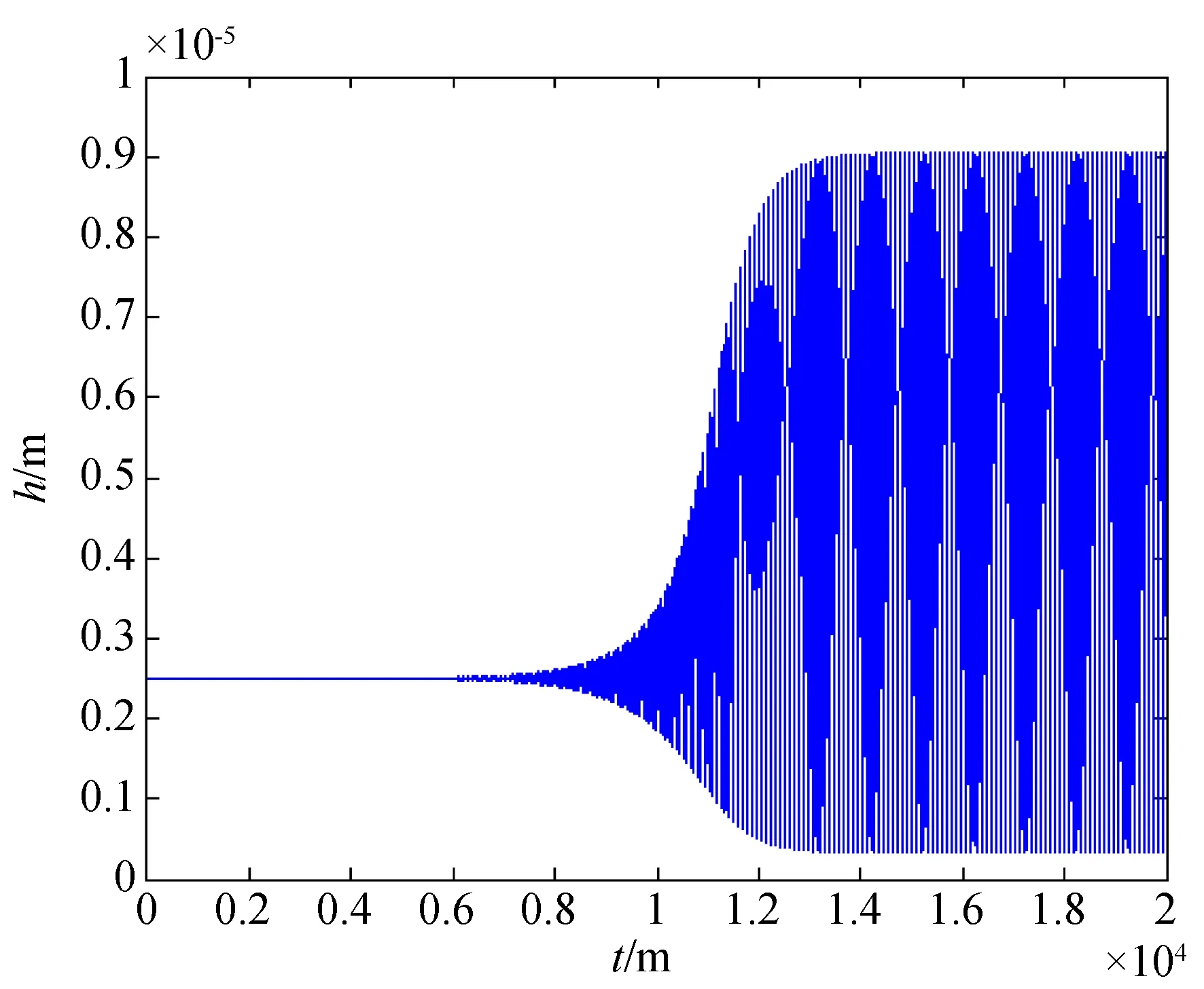
图5 气体静压轴承气锤失稳状态Fig.5 Air hammer instability state of aerostatic bearing

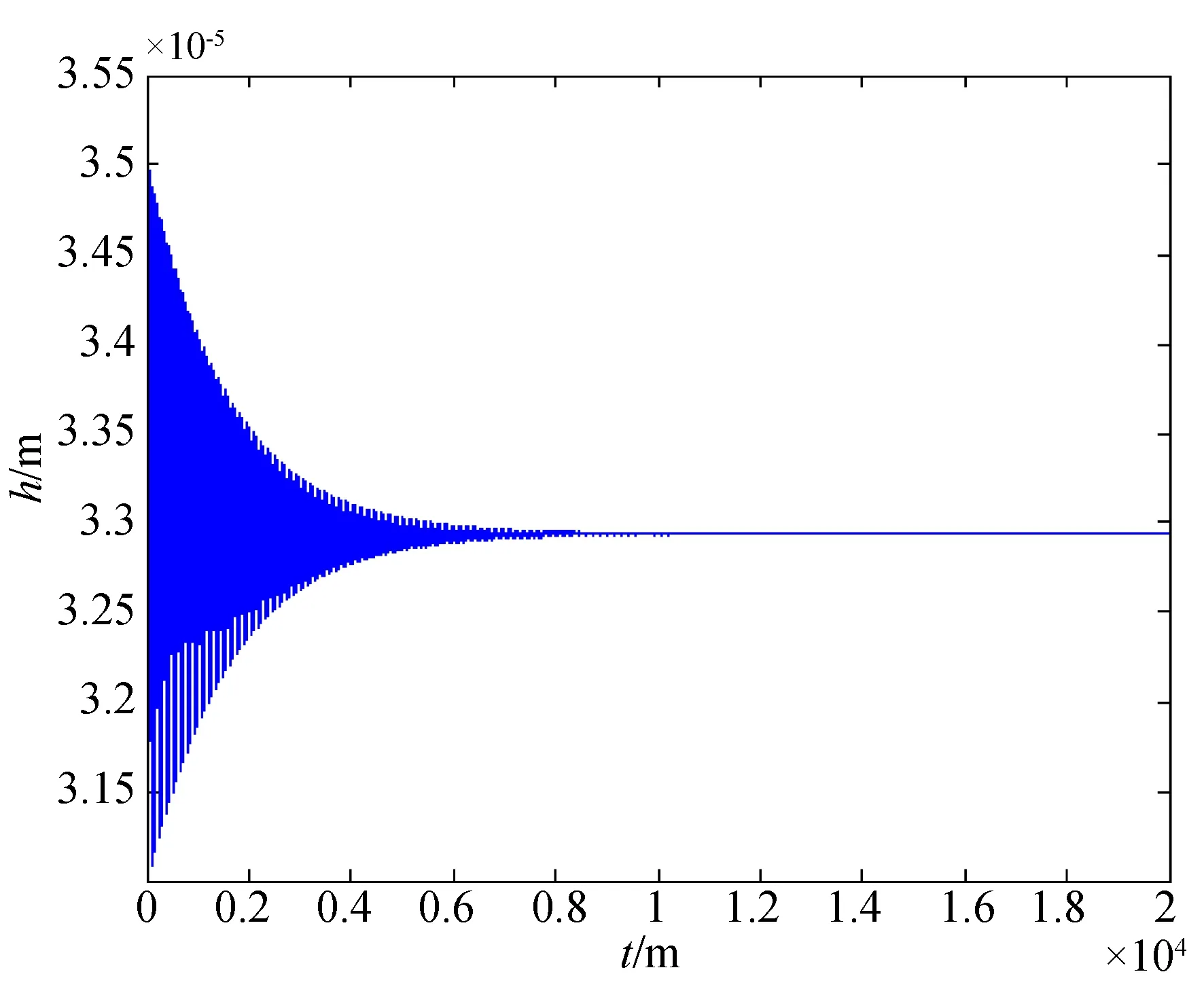
图6 气体静压轴承稳定状态Fig.6 Stability state of aerostatic bearing

在此基础上，分析气体静压轴承的工作气压随时间的变化情况。在气体静压止推轴承自激变化过程中，气膜间隙与气膜压力随时间变化的相位关系如图7和图8所示。

可以看出，气体静压轴承在自激失稳前后，气膜间隙与气膜压力随时间的变化存在明显的相位对应关系。在轴承稳定状态，二者相位0°，为同相位；当发生轴承自激失稳后，二者相位180°，为反相位。而且在轴承由失稳到稳定的变化过程中，随着工作时间的变化，两者的相位逐渐发生变化。因此，气膜间隙与气膜压力之间的相位关系可以反映气体静压轴承的稳定状态，进而验证了基于相位致振的气体静压轴承气锤失稳理论的有效性。

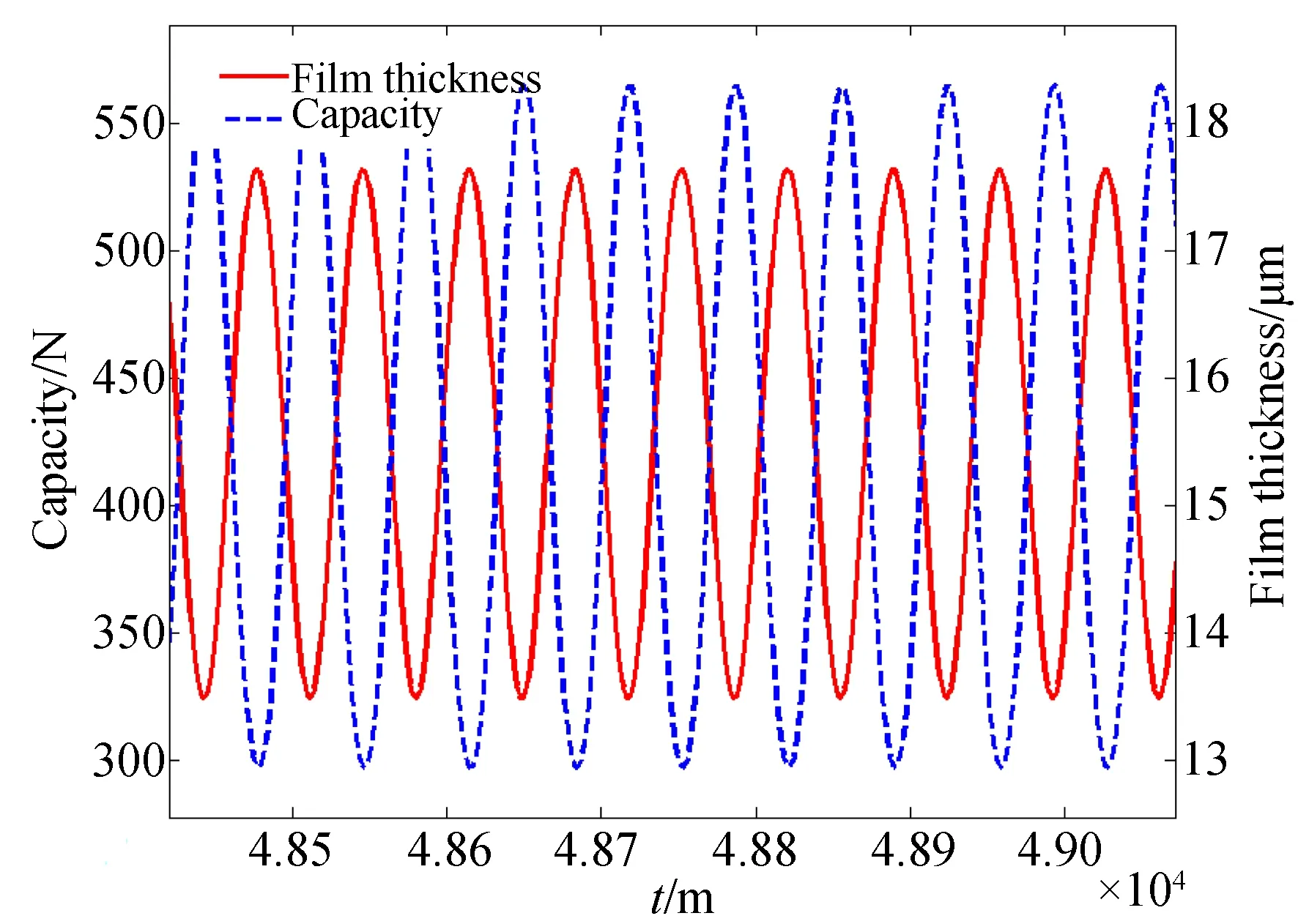
图7 气锤失稳状态下气膜间隙和承载与时间关系Fig.7 Relationship between film thickness and capacity under air hammer instability

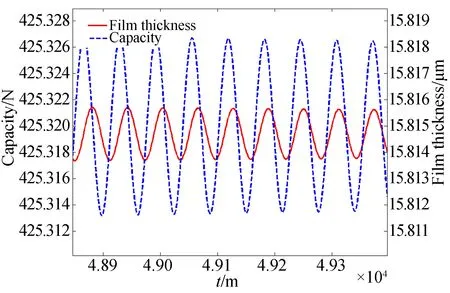
图8 渐稳状态下气膜间隙和承载与时间关系Fig.8 Relationship between film thickness and capacity under gradual stability

4 测量实验与结果

搭建如图9所示的测试装置，对前文所述的气体静压止推轴承的自激失稳理论分析进行试验验证。

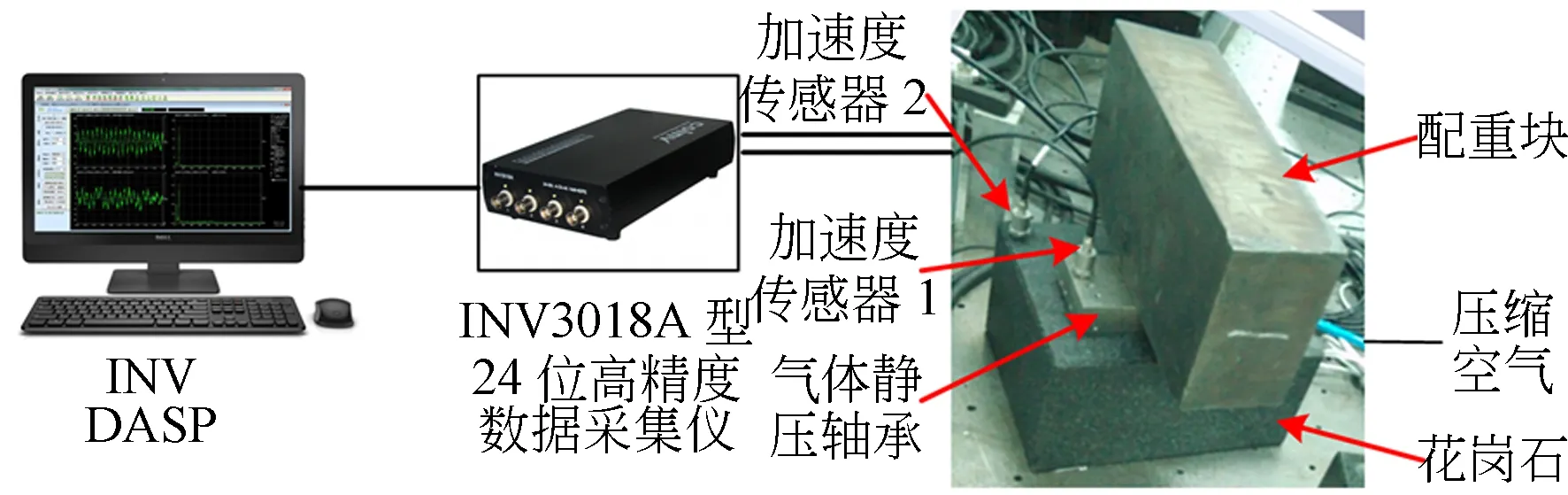
图9 气体静压轴承试验装置Fig.9 Experimental apparatus for aerostatic bearing

气体静压轴承的气锤失稳振动和非气锤振动的时域特性对比以及相图如图10～图12所示。由图可以看出，气锤失稳振动的幅值在9 μm，为单一频率的周期振动，非气锤振动的幅值为0.5 μm，为不规则的非周期振动。地面振动始终存在，但其幅值小于气体静压轴承的非气锤振动幅值。

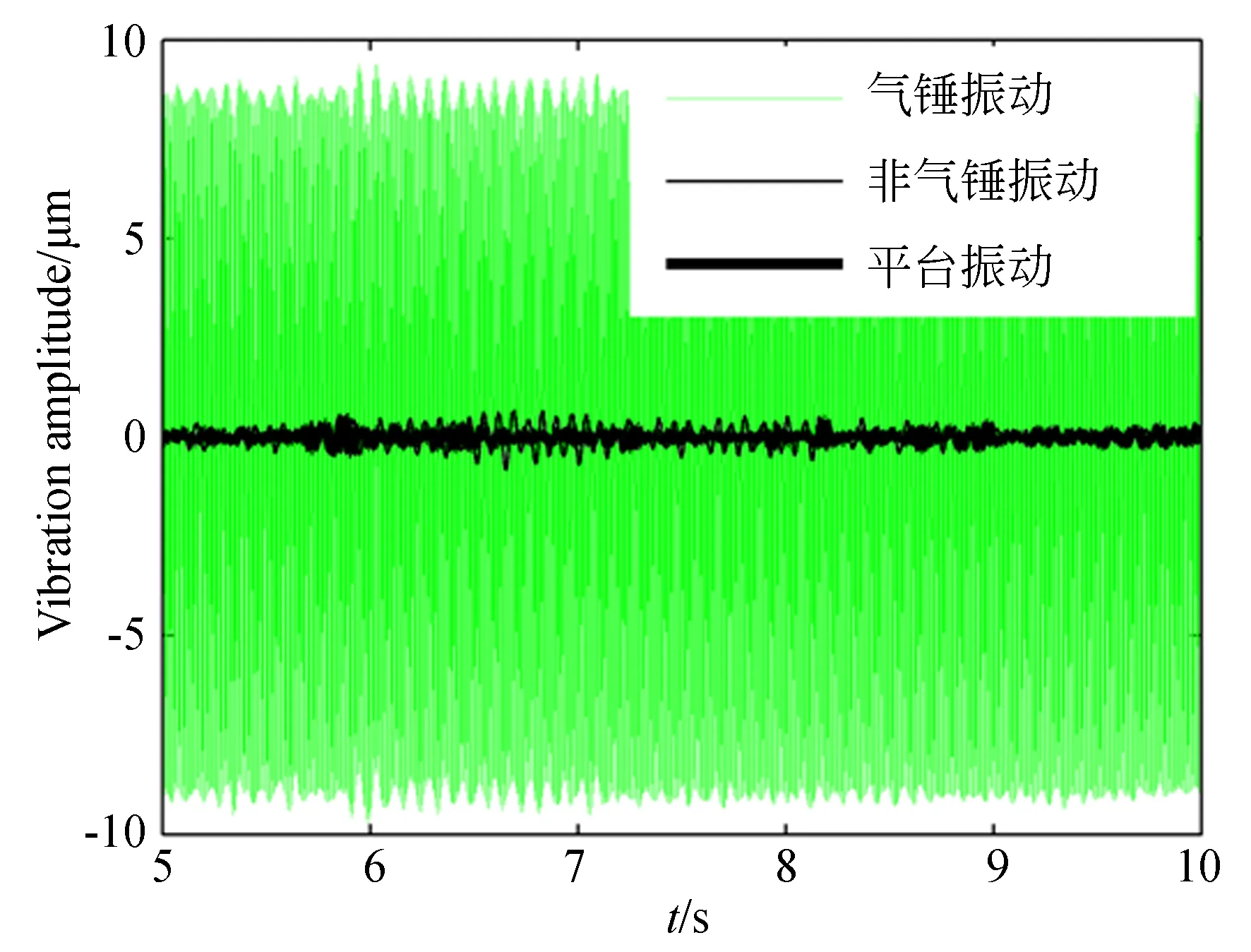
图10 气体静压止推轴承不同工况下振动特性Fig.10 Vibration characteristics of aerostatic bearing under different conditions

图11 气体静压止推轴承失稳状态相图Fig.11 Phase diagram of instability of aerostatic bearing

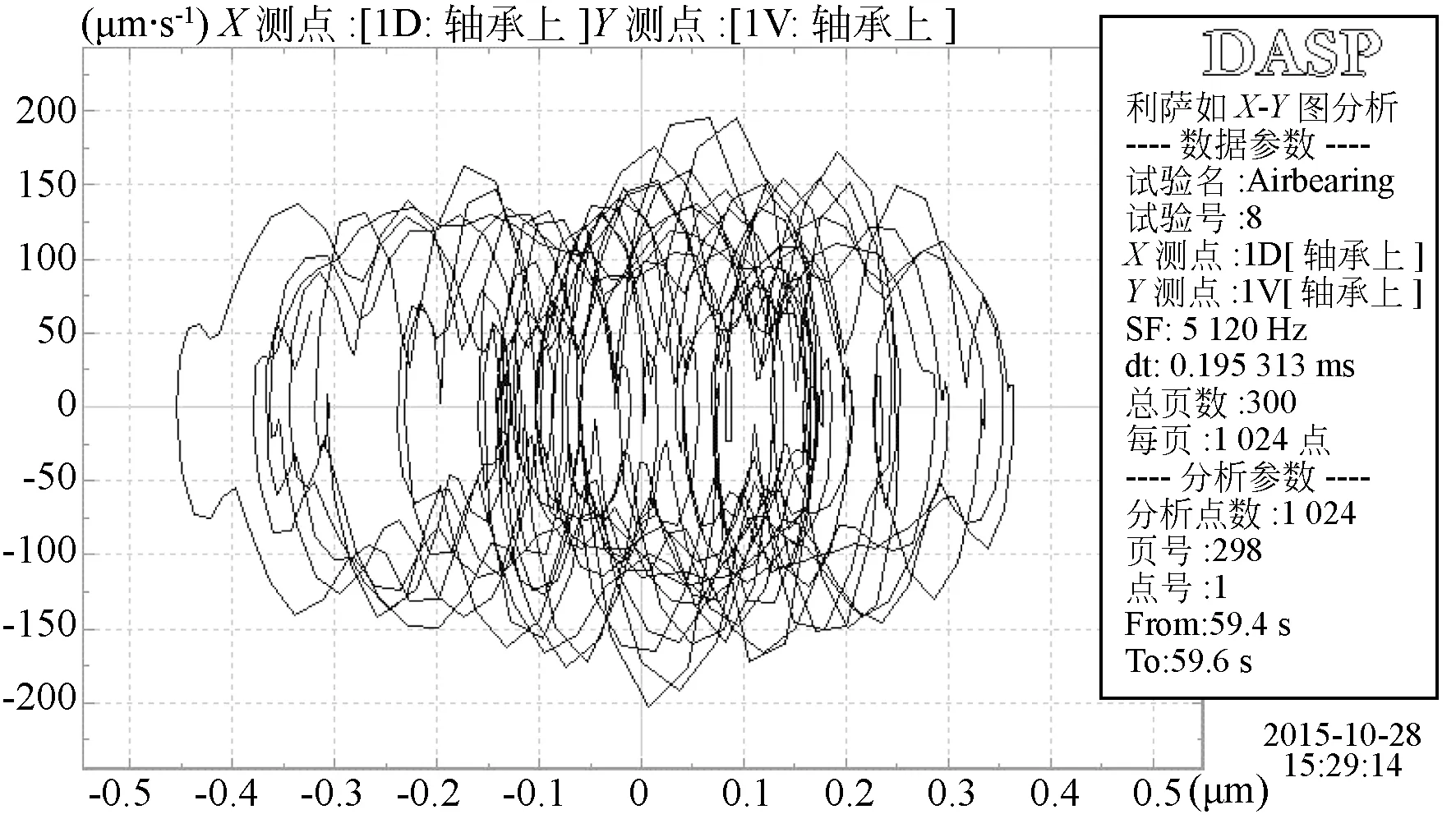
图12 气体静压止推轴承稳定状态相图Fig.12 Phase diagram of stability of aerostatic bearing

以气膜厚度和轴承运动加速度为研究对象，对气体静压轴承的气锤失稳在频率上进行Nyquist分析，分析结果如图13所示。由图可以看出，当频率的虚部为0时，此时相位差为180°，气体静压轴承发生了气锤失稳，与理论分析的结论一致，进而验证了理论分析的正确性。因此，未来将围绕着气体静压轴承中，气膜间隙与气膜压力相位变化的趋势进行进一步分析，研究气体静压轴承气锤失稳过程在相位上的表征，进而获得基于相位的气体静压轴承气锤失稳抑制方法。

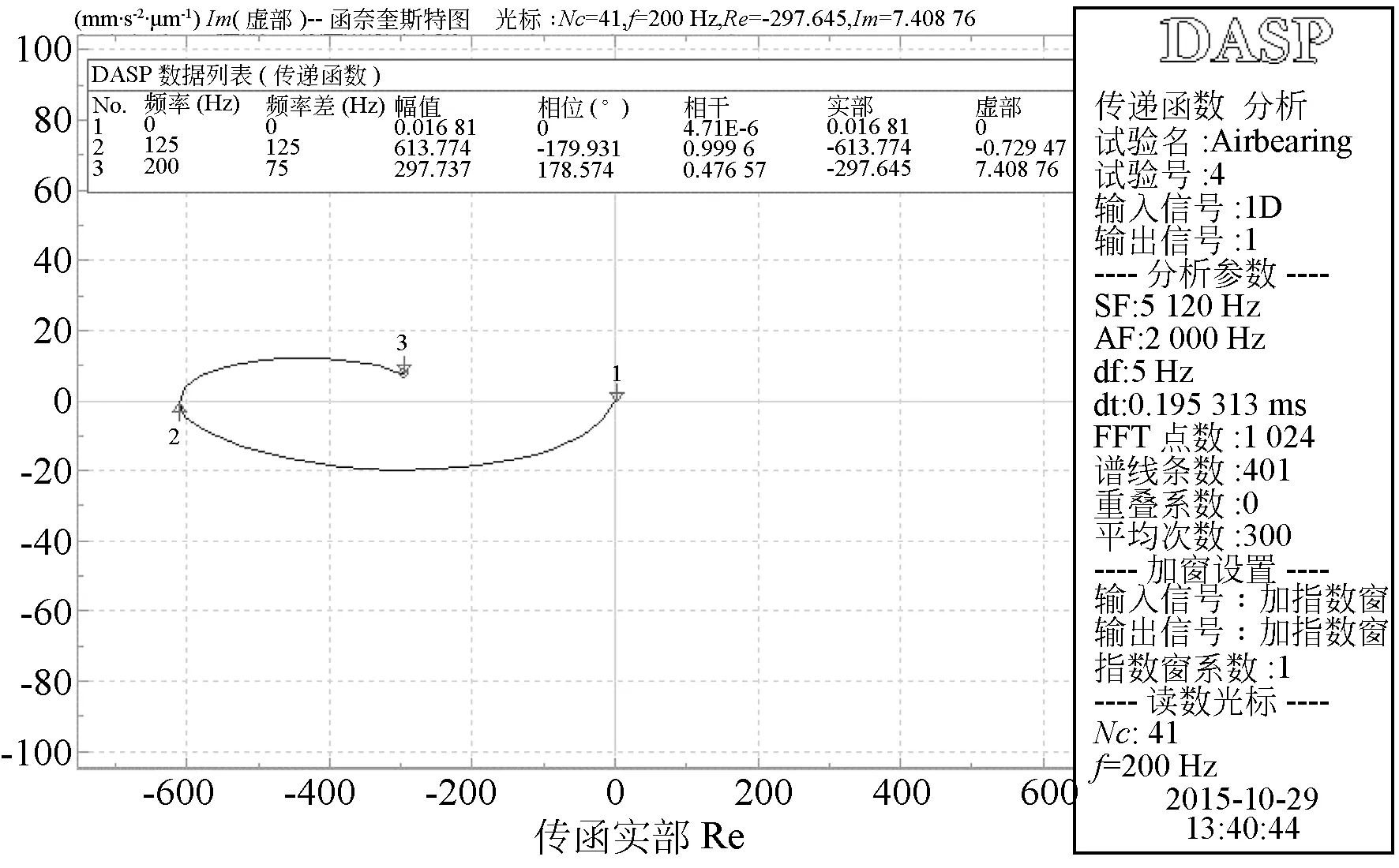
图13 气体静压轴承渐失稳状态下Nyquist分析图Fig.13 Nyquist plot of gradual instability of aerostatic bearing

5结 论

通过对气体静压轴承的动态特性进行精确建模，获得了特定工作参数下轴承气膜厚度与承载压力的相位关系，分析了气体静压轴承发生气锤失稳过程中的气膜厚度与承载的相位导致失稳的过程，并进行了试验验证。研究取得的成果如下：

建立了基于相位致振的气体静压轴承气锤失稳数学模型，通过该模型可以对气体静压轴承的动态稳定状态进行分析。

利用图解法分析了气体静压轴承稳定状态和失稳状态的时域特性，研究表明，气体静压轴承自激失稳前后，气膜间隙变化与气膜压力变化存在明显的相位对应关系。在轴承由稳定状态转至失稳状态过程中，二者相位从0°同相位逐渐变为180°反相位。因此，相位变化是气体静压轴承产生气锤失稳的表征形式之一，可以通过相位变化角度解释气体静压轴承发生气锤失稳的作用机理。

对理论分析结果进行了试验分析，试验研究验证了理论分析的正确性。因此，未来可以通过控制气体静压轴承中，气膜间隙变化与气膜压力的相位关系，来抑制轴承的气锤失稳振动。